当前位置：文档之家 › 高二数学曲线和方程PPT优质课件

高二数学曲线和方程PPT优质课件

  • 格式：ppt
  • 大小：228.00 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

高二数学曲线与方程PPT精品课件

高二数学曲线与方程PPT精品课件

• P(x0, y0)
点 P 到 原 点 的 距 离 为 5
x02y0225
(x 0 ,y 0 )是 方 程 x2y22 5 的 解 。
x2y2 25
( 2 ) 设 （ x 0 , y 0 ) 是 方 程 x 2 y 2 2 5 的 解 。
x02y0225 x02y02 5
M (x 0 ,y 0 ) 求 的 方 程 为 ： x4y120
例 3 ： 两 个 定 点 的 距 离 为 6 ， 点 M 到 两 个 定 点 的 距 离 的 平 方 和 为 2 6 ，
求 点 M 的 轨 迹 方 程 ？
解 ： 建 立 如 图 所 示 的 坐 标 系 ， 设 A （ - 3 ， 0 ） ， B （ 3 ， 0 ） ,
( 2 ) 设 点 M 的 坐 标 （ x , y ) 是 方 程 ： x 4 y 1 2 0 的 解
x4y12 M A (x 1 )2 (y 1 )217y2102y170
MAMB M B(x 1 )2 (y 7 )2 17y2102y170
x 4 y 1 2 0 的 解 为 坐 标 都 在 线 段 A B 的 垂 直 平 分 线 上
小结：曲线和方程的关系
点M
按 某 中 规 律 运 动 曲线C
几何意义
x,y的 制 约 条 件
坐标(x,y)
方 程 f(x,y)0
代数意义
“数形结合” 数学思想的基础
例 2 ： 设 A ， B 两 点 的 坐 标 为 （ 1 ， - 1 ） ， （ - 1 ， 7 ） ， 求 线 段 A B 的 垂 直 平 分 线 的 方 程 ？
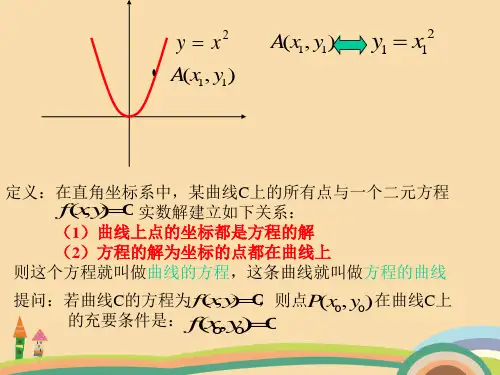
y x2
• A(x1, y1)
A(x1, y1)
y1 x12

曲线与方程 课件(共35张PPT)

曲线与方程 课件(共35张PPT)
曲线与方程
最新考纲展示
1．了解方程的曲线与 曲线的方程的对应关系．
2.了解解析几何的基本 思想和利用坐标法研究几 何问题的基本方法．
3.能够根据所给条件选 择适当的方法求曲线的轨 迹方程．
一、曲线与方程的定义 一般地，在直角坐标系中，如果某曲线C上的点与一个二元方
程f(x，y)＝0的实数解建立如下的对应关系：
(2)证明：设 E(xE，yE)，F(xF，yF)，依题意，
y＝k1x＋3，
由y92＋x2＝1
⇒(k21＋9)x2＋6k1x＝0，①
解得 x＝0 或 x＝－k216＋k19. 所以 xE＝－k216＋k19，yE＝k1－k216＋k19＋3＝2k721－＋39k21， ∴E－k126＋k19，2k721－＋39k21. ∵k1k2＝－9，∴k2＝－k91.用 k2＝－k91替代①中的 k1， 同理可得 Fk126＋k19，3kk2121－ ＋297. 显然 E，F 关于原点对称，∴直接 EF 必过原点 O.
曲线的交点问题(师生共研)
例 2 (2015 年南京模拟)设 0<θ<π2，曲线 x2sin θ＋y2cos θ＝1 和 x2cos θ－y2sin θ＝1 有 4 个不同的交点．
(1)求θ的取值范围； (2)证明：这4个点共圆，并求圆的半径的取值范围．
解 析 (1) 两 曲 线 的 交 点 坐 标 (x ， y) 满 足 方 程 组 x2sin θ＋y2cos θ＝1， x2＝sin θ＋cos θ， x2cos θ－y2sin θ＝1， 即y2＝cos θ－sin θ.
D．以上答案都不对
(2)(2015年广州模拟)下列说法正确的是( )
A．△ABC中，已知A(1,1)，B(4,1)，C(2,3)，则AB边上的高的方

高二数学课件：曲线与方程新人教版A版

高二数学课件：曲线与方程新人教版A版

整理ppt
6
例2.已知一条直线l和它上方的一个点A，点A到l的距 离是2,一条曲线也在l的上方，它上面的每一点到A的 距离减去到l的距离的差都是2,建立适当的坐标系，求 这条曲线的方程.
解：取直线l为x轴,过点A且垂直于直线l的直线为y轴,
建立坐标系xOy设, 点M(x,y)是曲线上任意一点，
MB⊥x轴，垂足是B， 1）建系设点
x 2 y 2 a 2 x a
整理ppt
13
￥探索性练习
已知线段AB的长为6，动点P到A，B的距离平 方和为26，求动点P的轨迹方程（课本P37习题 2.1A组第3题）。
分析:利用坐标法求曲线方程要先有（或 建立）坐标系．
在具体问题中：一种是给定了坐标系；另一种 是没给定坐标系，需自己建立适当的坐标系．
x2 y2 a2 （xa） 整理ppt
10
法2：BCCA C
kBC •kAC 1 A
B
yy
xa
1 xa
即x2
y2
a2
由A、B、C三点不共线，
xa，即直角顶点C的 程轨 为迹
x2 y2 a2 （xa）。
整理ppt
11
法3： 连结OC
OAOB且BCCA
OC1 ABa C 2
x2 y2 a
A
O
整理ppt
2
复习回顾
1.复习曲线的方程和方程的曲线的概念
2. 练习： (1) 设A(2,0)、B(0,2)，
能否说线段AB的方程为x+y-2=0? (2) 方程x2-y2=0表示的图形是_______
3.证明已知曲线的方程的方法和步骤
1曲线上的点的坐标都是方程的解
2以方程的解为坐标的点都在曲线上

高二数学曲线和方程PPT优秀课件

高二数学曲线和方程PPT优秀课件
点练。习： 1.若命题“曲线上的点的坐标都是方程f(x,y) 的解”是正确的，试判断下列命题的真假： (1)不是曲线上点的坐标一定不满足f(x,y)=0. (2) 坐标满足方程f(x,y)=0的点在曲线上。 (3)曲线C是方程f(x,y)=0的曲线。 (4)不是方程f(x,y)=0的解，一定不是曲线C上 的点。
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
x
O
x
A
Hale Waihona Puke BC• ①曲线上的点的坐标都是这个方程的解； • ②以这个方程的解为坐标的点都是曲线上的点。
练习：请标出下列方程所对应的曲线 (1) x y0 (2)x2y2=0 (3)|x|y=0
y
y
y
O
x
O
x
O
x
A
B
C
• ①曲线上的点的坐标都是这个方程的解； • ②以这个方程的解为坐标的点都是曲线上的
M(x0,y0)是C上的点
(x0,y0)是方程y=2x2 (1 x 2) 的解
y
l
8
C
1
x-y=0
O1 x
2 -1 O
y=2x2(1 x 2) 2x
•
定义：在直角坐标系中，如果某曲
线C(看作适合某种条件的点的集合或轨
迹)上的点与一个二元方程f(x,y)=0的实数
解建立了如下的关系：
•
①曲线上的点的坐标都是这个方
例1.(1)画出两坐标轴所成的角在第一、 三象限的平分线 l ，并写出其方程.
(2)画出函数y=2x2(1 x 2)的图象C
曲线 ? 方程
点
(x,y)
y
l

高二数学选修2-1课件抛物线及其标准方程新人教A版1.ppt

高二数学选修2-1课件抛物线及其标准方程新人教A版1.ppt
例1. 若点M到定点F(5，0)距离和它到
定直线 l : x 16 的距离的比是常数 5 ，
5
求点M的轨迹方程.
x2
y2
4
11Biblioteka 91、若点F是定直线l外一定点，动点M 到点F的距离与它到直线l的距离之比等 于常数e(e>1)，则点M的轨迹是双曲线
吗？ 是！称为双曲线的第二定义
试与椭圆的第二定义比较
B1
B
4. |
11 AF | | BF |
1 p
5.A,O, B1三点共线.
直线与抛物线的关系
尝试练习
已知抛物线y2=4x,过定点A(-2, 1)的直 线l的斜率为k,下列情况下分别求k的取值 范围： 1. l与抛物线有且仅有一个公共点； 2. l与抛物线恰有两个公共点； 3. l与抛物线没有公共点.
移动，F是抛物线的焦点，则|MF|+|MA|
的最小值是( 3 ),此时M的坐标是 (( 1 ,1) )
5.已知M是抛物线
y
1
4
x2上一动点，M
4
到其准线的距离为d1 , M到直线x+y=2的
距离为d2 , 则d1+d2的最小值是( 3 2 ).
2
y2 16x.
6. 若点M到点F（4，0）的距离比它到
直线l:x＋5＝0的距离少1，求点M的轨
迹方程.
yM
l
y2 16x或x2 8y.
y2 16x.
OF x
7.如图，一个动圆M与一个定圆C外切， 且与定直线l相切，则圆心M的轨迹是什 么？
M
l
C
以点C为焦点的抛物线.
例1 一种卫星接收天线的轴截面如图
所示，卫星波束呈近似平行状态射入轴

高中数学 第二章《曲线和方程》课件 新人教版选修2-1

高中数学 第二章《曲线和方程》课件 新人教版选修2-1

以方程的解为坐标的点都在圆O上
所以：方程是圆O的方程 圆O是方程表示的圆
ppt精选
5
一般地，在直角坐标系中，如果某曲线C上 的点与一个二元方程 f(x，y)=0的实数解建立了 如下的关系：
（1）曲线上点的坐标都是这个方程 的解； （2）以这个方程的解为坐标的点都ቤተ መጻሕፍቲ ባይዱ曲线上的点；
那么这个方程叫做曲线的方程；这条曲线叫做方程 的曲线（图形）。
曲线和方程
ppt精选
1
知识探究
设直线L表示直角坐标系 中平分第一、三象限的
y M
直线
Ox
L
1.如果点M（x0，y0） 是直线L上任意一点， 点M的坐标是方程
x－y=0 的解吗？
直线L上所有点的坐标 都是方程的解
ppt精选
2
知识探究
2.如果x0，y0是方程x－y＝0的解， 那么点
M（x0，y0）一定在直线L上吗？
ppt精选
10
想一想：
证明已知曲线的方程的方法和步骤
第一步，设M (x0,y0)是曲线C上任一点， 证明(x0,y0)是f(x,y)=0的解；
第二步，设(x0,y0)是f(x,y)=0的解，证 明点M (x0,y0)在曲线C上.
ppt精选
11
练习: 证明以原点为圆心，半径等于5的圆的方程是x2 +y2 = 25, 并判断点M1(3，-4)，M2(-3，2)是否在这个圆上.
想一想： 如果曲线C的方程是 f(x，y)=0，那 么点P0(x0 ，y0)在曲线C 上的 充要条件是
f(x0，y0)=0 .
ppt精选
6
例1、下列各题中，图所示的曲线C的方程为所列方程，对吗？ 如果不对，是不符合关系⑴还是关系⑵？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1．坐标法．
他没有把x，y看成是未知数，而 是创造性地把x看成是变量(从此，变 量引入了数学)，让x连续地变，则对 每一个确定的x值，一般来说都可以 从方程f(x，y) = 0算出相应的y值(这就 是函数思想的萌芽)．然后，他把这些 点的集合构成了一条曲线C．由这样 得出的曲线C和方程f(x，y) = 0有非常 密切的关系：
2．解析几何的创立意义及其基本问题
他们创立解析几何，在数学史上 具有划时代的意义：
一是在数学中首次引入了变量的 概念，二是把数与形紧密地联系起来 了．
解析几何的创立是近代数学开端 的标志，为数学的应用开辟了广阔的 领域．
3．平面解析几何研究的主要问题．
(1) 根据已知条件求出表示平面 曲线的方程；
yP
B
M
O
Ax
小结：求简单曲线方程的一般步骤:
(1)建立适当的坐标系，用有序实 数对表示曲线上任意一点M的坐标；
(2)写出适合条件P的点M的集合； (3)用坐标表示条件P(M)，列出方 程f(x，y) = 0； (4)化方程f(x，y) = 0为最简形式； (5)证明以化简后的方程的解为坐 标的点都是曲线上的点．(可省)
求轨迹方程的过程较简单．所求方程
的形式较“整齐”．
练习 1. 点P到点F(4，0)的距离比它到
直线x + 5 = 0的距离小1，求点P的轨
迹方程．
y2 = 16x．
2. 过点P(2，4)作互相垂直的直线
l1，l2，若l1交x轴于A，l2交y轴于B，
求线段AB中点M的轨迹方程．
x + 2y 5 = 0．
OQ x
垂足．
因为点M到x轴、y轴的距离分别
是它的纵坐标和横坐标的绝对值，所
以条件|MR| = |MQ|可写成| x | = | y |， 即x ± y = 0 ①
即x ± y = 0 ①
下面证明①是所求轨迹的方程．
(1) 由求方程的过程可知，曲线上
的点的坐标都是方程①的解； (2) 设点M1的坐标(x1，y1)是方程
例1设A、B两点的坐标是(1，0)、 ( 1，0)，若kMA kMB = 1，求动点 M的轨迹方程．
x2 + y2 = 1 (x ± 1)
说明：所求的方程x2 + y2 = 1后 面应加上条件x ± 1．
例2点M到两条互相垂直的直线的
距离相等，求点M的轨迹方程．
解：取已知两条 互相垂直的直线为
y RM
坐标轴，建立直角
OQ x
坐标系如图所示．
设点M的坐标为(x，y)，点M的轨迹 就是到坐标轴的距离相等的点的集合
P = {M | |MR| = |MQ|}，
例2点M到两条互相垂直的直线的
距离相等，求点M的轨迹方程．
P = {M | |MR| = |MQ|}，
y
其中Q、R分别是点
RM
M到x轴、y轴的垂线的
①的解，那么x1 ± y1 = 0，即 | x1| = | y1|，而| x1|、| y1|正是点M1
到纵轴、横轴的距离，因此点M1到这 两条直线的距离相等，点M1是曲线上 的点．
x±y=0 ①
由 (1)(2) 可 知 ， 方程①是所求轨迹 的方程，图形如图
y RM OQ x
所示．
点评：建立适当的坐标系，能使
1．坐标法．
在笛卡尔以前，人们对代数方程 已经有了一定的研究，但是对于二元 方程的研究较少，因为大家认识到二 元方程f(x，y) = 0的解都是不确定 的．对于这种“不定方程f(x，y) = 0”， 除了有少数人研究它的整数解以外， 大多数人都认为研究它是没有意义的， 是不必要的．笛卡尔却对这个“没有 意义的课题”赋予了新的生命，
1．坐标法．
曲线上每一个点的一对坐标都是 方程的一个实数解；反之，方程的每 一个实数解对应的点都在曲线上．这 就是说，曲线上的点集和方程的实数 解集具有一一对应的关系．这个“一 一对应”的关系导致了曲线的研究也 可以转化成对曲线方程的研究．
1．坐标法．
这种通过研究方程的性质，间接 地来研究曲线性质的方法叫做坐标法 (就是借助于坐标系研究几何图形的方 法)．
根据几何图形的特点，可以建立 不同的坐标系．最常用的坐标系是直 角坐标系和极坐标系．在目前的中学 阶段只采用了直角坐标系．
2．解析几何的创立意义及其基本问题
在数学中，用坐标法研究几何图 形的知识形成的一门学科，叫解析几 何．它是一门用代数方法研究几何问 题的数学学科，产生于十七世纪初 期．
法国数学家笛卡尔是解析几何的 奠基人．另一位法国数学家费马也是 解析几何学的创立者．
(2) 通过方程，研究平面曲线的 性质．
本节主要通过例题的形式学习第 一个问题，即如何求曲线的方程．
4．求简单曲线方程的一般步骤：
(1)建立适当的坐标系，用有序实 数对表示曲线上任意一点M的坐标；
(2)写出适合条件P的点M的集合； (3)用坐标表示条件P(M)，列出方 程f(x，y) = 0； (4)化方程f(x，y) = 0为最简形式； (5)证明以化简后的方程的解为坐 标的点都是曲线上的点．
定义(教材P68)：在直角坐标系中， 如果某曲线C上的点与一个二元方程f(x， y) = 0的实数解建立了如下关系：
(1) 曲线上的点的坐标都是这个方 程的解；(点不比解多) (纯粹性)
(2) 以这个方程的解为坐标的点都 是曲线上的点． (解不比点多) (完备性)
那么，这个方程叫做曲线的方程； 这条曲线叫做方程的曲线(图形)．
THANKS FOR WATCHING
谢谢大家观看
为了方便教学与学习使用，本文档内容可以在下载后随意修改，调整。欢迎下载！
汇报人：XXX
时间：20XX.XX.XX
2021/