2020年英语中考冲刺四：阅读理解技巧(基础讲解) -精选

2020年疫情期间的新疆最新中小学暑假放假时间疫情出现，影响了我们的生活水平，学生们也无法按时回校上课，开学时间也一再延迟，暑假时间也有一定的影响，最近新疆的中小学暑假放假时间公布了，想要知道是什么时候吗?下面是小编为大家带来的有关2020年疫情期间的新疆最新中小学暑假放假时间，希望大家喜欢。

2020年疫情期间的新疆最新中小学暑假放假时间2020年新疆暑假时间为：2020年7月3日。

如何让孩子在暑假里更好地实行学习计划1. 父母少插手，多监督一位家长最近正在用这套方法和图表，帮助两个孩子做时间管理。

她以前帮孩子做时间管理的时候，都是她把计划表都安排好了，而这次她只是提供了纸和便利贴以及图表模板。

她发现孩子的积极性高了很多，会认真去思考完成每件事应该按什么先后顺序，每件事大概需要多少时间等。

做好了计划后，也会认真把每件事完成。

孩子的自我参与度越高，责任感和成就感就越强。

另外，孩子自觉度并不高，父母要每天睡觉前监督一下，看看孩子是不是完成了时间轴上的每一件事。

2. 完成有奖，没完成有罚有奖有罚，才会有积极性。

奖励方法可以试试每完成一天的任务，就奖励一个勋章，集齐10个就奖励孩子想要的东西或者是零花钱。

惩罚方法可以试试没完成当天的任务，就取消当天的玩游戏时间。

3. 注意随时调整计划计划赶不上变化。

如果孩子尽力了，发现某件事每天要花的时间比计划的时间要长，家长就要注意和孩子一起调整计划。

如果暑假期间有突发事情打断了计划，家长也要和孩子一起调整计划。

随着学业越来越重，孩子拼的不仅仅是学习能力，还有时间管理能力。

一个暑假并不能立即提升孩子时间管理的能力，但至少可以让孩子了解什么是时间管理，以后持之以恒，最后就会养成高效利用时间的好习惯。

暑假如何安排孩子的假期生活1、结合学校安排的学习任务给孩子制定暑假计划表，让孩子严格去完成计划表中的事情。

对于孩子完成的作业，进行检查，给予讲解和指导。

2、给孩子报个补习班或者是兴趣爱好班，让孩子去学习自己感兴趣的东西，如果孩子功课不好，就让孩子去上补习班巩固学习。

2020高中数学高效学习方法全攻略高中数学应该如何学习?今日小编给大家分享高中学习数学时遇到的一些问题案例以及一些高中数学的学习技巧，希望对正处于高中阶段，想学好数学的同学，能提供到一定的帮助。

一.高中数学之于我的契机数学，在高考中是作为我的强项的。

但在整个高中阶段，我并非从一开始就能快速的掌握学习的技巧和方法。

高一刚开始，身处于直升班的我，在班里领悟力不算强，智商也并不算高，因而很长一段时间里，我对于自己的数学学习都完全没有信心。

初中总体来说成绩还不错，因而全校两个校区择100人的保送本校高中部，我作为最后几名勉强进了名单。

五月份，在大家还在为中考而努力的时候，我们已经提前开始了高中生活。

但因为对应的任课老师还在为当时的高三年级最后的冲刺而努力，所以说是提前的适应，其实就是每天早上老师留一道思考题，让我们用一天的时间去琢磨。

那两个月，我人生中第一次深刻体会到了智商的差异(虽然在之后的日子里，被智商碾压已成常态，笑)。

有道题我现在还记得，而且对我高中三年的影响颇大。

“在一个边长为1m的封闭立方体中，放置一个半径为0.1m的小球。

小球可以在立方体中随意的运动，求小球滚不到的部分的体积。

”现在看来，似乎并不难。

但对于当时的我而言，真的是莫大的难题。

身边的同学一个个算出了答案，而我的小球还在脑子里不停地旋转跳跃不停歇。

我怎么都想不明白，那个球究竟会怎么动。

我甚至用木板做了一个立方体出来，每天抱在怀里，拿个小乒乓球放在里面，每天盯着看。

终于有一天，我想清楚了。

尽管比别人慢了很多，但我真真正正地想明白了。

没有人会觉得这是什么了不起的事情，但对于我，确实是一件令我十分开心的成就。

它让我明白了，哪怕我不如别人聪明，但别人能做的事情，我也总归是能完成的，而且，也许会在质量上完成得更好。

而且，从那道题开始，在立体几何方面，我仿佛开窍了一般，豁然开朗。

我开始喜欢动脑子，喜欢那种琢磨很多天，忽然一刻想通了的感觉，开始喜欢上数学。

2019-2020学年第二学期九年级下册道法教学计划2019-2020年度第二学期九年级下册道法教学计划XXX本学期是学生升学考试关键的一学期，九年级道法科教学、复课时间少、时间短、任务紧。

扎实搞好中考复，是取得理想成绩的前提条件，科学有效地研究和复，有助于提高学业成绩。

今年除了道法中考复的一般情况外，由于疫情的影响，正常开学推迟，虽然学生上网课，但是据我的了解学生的研究效果并不好，所以，必须采取相应的对策。

为了进一步巩固学生初中三年所学道法的知识，以及学生对所学道法知识的理解和应用，有效的提高学生中考考试的学业成绩，按照学校及教研组的安排，特制定九年级道法学科教学、复计划。

一、指导思想让学生巩固初中阶段道法课程中重要的内容知识点，学生能够灵活的应用和理解所学的知识，学会考试的一些方法和技巧，有效的提高学生中考考试的研究成绩。

教研组教师精诚团结、取长补短、资源共享、注重实效，以集体的力量确保学科优势。

二、学生基本情况分析本校九年级学生通过两年半初中道法课的研究，对初中道法科有了较好的了解，能基本掌握初中道法科的基本理论知识及研究方法。

但由于受家庭、社会的影响，学生的思想波动性比较大，有部分学生只顾贪玩和享乐，不重视研究成绩，有厌学和打算读中专学校的现象。

有上进心的一部分学生在研究过程中也存在知识学的不活，缺乏研究自主性和积极性，没2019-2020学年第二学期九年级下册道法教学计划有科学的复策略，独立分析问题、解决问题的能力还有待提高。

因此，这一个学期要尽快转变不良学风，加强对后进生的心理引导，帮助学生制定科学的复计划，提高学生的学业成绩，使他们能够顺利的毕业，考上更高学校，教师必须要下一番苦功夫。

三、复内容1、七年级上、下册2、八年级上、下册3、九年级上、下册4、安徽省中考道法课程标准，复、研究方法指导，不良考试心理指导，厌学心理纠正。

5、综合模拟能力训练。

6、专题复和时事、社会热点复四、复措施(一)、单元复，夯实基础初中道法中考主要是考查学生对基础知识的掌握情况及应用基础知识分析思想、行为、社会生活的能力。

紧急！全国多地严禁招收复读生，2021高考考生将失去“复读”机会！高考复读作为我国多年来的一种特殊教育现象。

近年来，虽官方未公布具体数据，但从各方渠道透露出的消息可知，每年都有不少的考生因为各种原因选择复读再次参加高考，使得复读生群体愈发庞大。

在每年大学招生人数几乎固定的情况下，高考复读生越多自然就会导致应届生落榜者越来越多，然后落榜的应届生再去复读，从而形成恶性循环。

为了避免这种情况，多地教育厅纷纷颁布相关通知。

近日，湖南某教育局发布《关于做好2021年全市普通中小学招生入学工作的通知》，通知中指出：要切实规范招生行为，公办普通高中不得招收复读生。

在2020年之前，很多地区也发布了类似通知；贵州：2020年4月21日，贵州省教育厅发布《关于规范普通中小学招生工作的通知》称，从2020年开始，全面禁止公办普通高中招收复读生。

四川：2020年4月8日，四川省教育厅发布《关于规范2020年全省普通中小学生招生入学工作的通知》，其中也提到，省级示范性普通高中不得举办复读班，举办复读班的学校需严格登记学生信息情况。

云南：2019年10月14日云南省教育厅发布《云南省中小学生减负措施》中明确指出，普通高中一律不得招收借读生、择校生、公办普通中学不得招收复读生。

黑龙江：普通高中不得举办复读班。

其实，早在2002年2月份，国家教育部就颁发了《关于加强基础教育办学管理若干问题的通知》，通知中明确指出：一些地方公办学校招收高中毕业生复读的现象有增加的趋势。

使本来已经短缺的高中教育资源更趋紧张，也影响普通高中实施素质教育。

各级教育行政部门要加强管理和引导。

为扩大普通高中招生规模，从2003年秋季开学起，各地公办高中不得占用学校正常的教育资源举办高中毕业生复读班，也不得招收高中毕业生插班复读。

公办高中不得举办复读班，就意味着复读生们想要复读，就只能去民办高中或培训机构就读，这将大大加重家庭的经济压力。

另外，公办高中与民办高中/培训机构还有一个更大的区别，那就是师资水平差距！现在还在晚睡晚起、应付考试、上课溜神、熬夜打游戏的同学，你醒醒吧！任性妄为的自由并不是真的自由，它只是在拿你的未来买单。

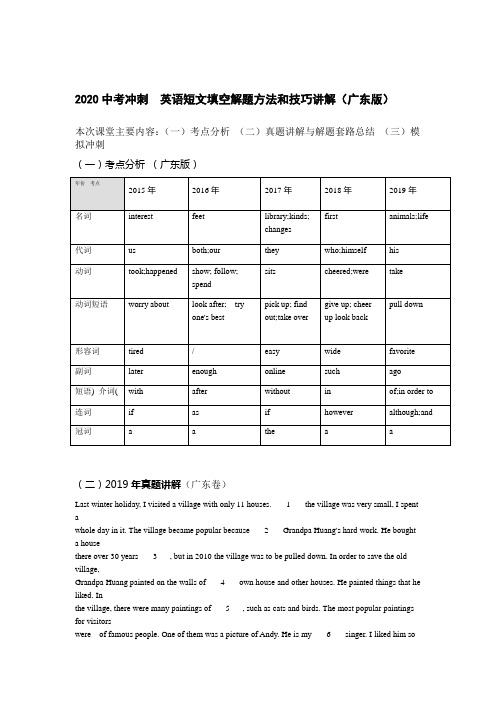
2020中考冲刺英语短文填空解题方法和技巧讲解（广东版）本次课堂主要内容：（一）考点分析（二）真题讲解与解题套路总结（三）模拟冲刺（一）考点分析（广东版）（二）2019年真题讲解（广东卷）Last winter holiday, I visited a village with only 11 houses. ___1___ the village was very small, I spent awhole day in it. The village became popular because ___2___ Grandpa Huang's hard work. He bought a housethere over 30 years ___3___, but in 2010 the village was to be pulled down. In order to save the old village,Grandpa Huang painted on the walls of ___4___ own house and other houses. He painted things that he liked. Inthe village, there were many paintings of ___5___, such as cats and birds. The most popular paintings for visitorswere of famous people. One of them was a picture of Andy. He is my ___6___ singer. I liked him somuch that Iasked a visitor to ___7___ a photo of that painting and me. On the ground of the village, Grandpa Huang haspainted ___8___ lot of well-known Chinese sayings. From them, Grandpa Huang learned to live a long and happy___9___. I really had a good time in the village _____10_____ wished to visit it again.1. 2. 3. 4. 5.6. 7. 8. 9. 10.【文章大意:】去年寒假，“我”参观了一个只有11栋房子的村庄。

中考冲刺五：任务型阅读技巧【真题再现】I. 阅读下面两篇短文，根据所给语境，按要求完成下列各题。

(2014 黄冈)You can buy chewing gum in nearly every country of the world. ①But it wasn’t always like that.The American Indians were the first people to chew gum. This gum came from a special tree that grew on their land. In 1848, a sailor called John Curtis began selling it. He was the first person to sell chewing gum. The gum he sold cost just a few cents for two pieces. It became popular very quickly even though it was very hard to chew. ②Nowadays, other things are added to the gum to make it soft and sweet.By 1890, there were hundreds of different chewing gums. The most famous name in chewing gum, however, is probably William Wrigley. He spent a lot of money in advertising and even sent free pieces of gum to children on their birthdays. ③ He also said that chewing gum helped people work better and that it stopped people from feeling tired.Although today many millions of people chew gum, not everyone thinks it is a good thing to do. Many people think it is dirty. The Singapore government does not allow people to buy chewing gum. One reason for this is that when some people have chewed all the taste out of their piece of gum, they take it out of their mouths and put it on to the backs of seats or other places.1. 请将①处翻译成汉语。

中考英语备考复习方法时光荏苒，光阴如梭，2020年的中考即将来临。

这几年的英语中考试题，不仅加强了对英语基础知识的考查，更突出了对运用知识的能力的考查。

下面是小编为大家整理的关于中考英语备考复习方法，希望对您有所帮助。

欢迎大家阅读参考学习!中考英语备考复习方法第一、回归基础。

词汇：词汇复习是复习基础知识和基础技能的第一阶段，中考考的就是根据原文将词或者短语填入短文中，这些词汇来源大部分是课文的绿色词语中，其中中考中6个字母以下的单词出现概率占80%左右，所以绿色词是词汇中第一个要注重的地方。

所以有空闲时间的父母家长可以将绿色词汇总起来，出一些中考模拟试题，直接让孩子填单词。

语法：中考英语语法主要从动词和从句入手。

动词变化多，要注意动词的时态和语态，要将现在时，将来时，过去时等基本概念搞清楚，做相应的练习，这样才能在应用中减少出错。

从句复习时，也是从时态入手，通常出题老师会给出过去时态，然后再让你填写或者选择时态的变化。

口语：口语方面要注重朗读的感情。

中考英语口语中，朗读题占5分，问答题占5分，口头表达题也占5分。

诵读的时候要求要能连贯地朗读，语调、节奏和语音基本正确，朗读充满情感才能得5分，所以建议考生每天花5分钟去有感情的诵读。

不少学生说平时不用注意感情，到考试的时候再加感情进去就行。

这种想法是错误的，因为口语感情要平时积累，考试的时候如果没有做好基本功，根本就没有时间反应过来。

还有问答的时候，要注意一些技巧。

第二、深入扩展。

听力方面，要提升技巧要有一个好的复习方案，可以从日常生活中下手，如从歌曲中，新闻中，还有电影中来提升英语听力能力。

阅读方面，建议看一些全英文的书籍，出版商要是英国或者美国，中国人翻译过来的书籍都不够“原味”。

第三、2020中考新情况。

今年英语路不考反义疑问句，定语从句和阅读预测下文会出题目。

反义疑问句不考，考生复习的时候可以直接省略。

初三英语复习备考时光荏苒，光阴如梭，2020年的中考即将来临。

中考冲刺：创新、开放与探究型问题—知识讲解（提高）【中考展望】所谓开放探索型问题指的是有些数学问题的条件、结论或解决方法不确定或不唯一，需要根据题目的特点进行分析、探索，从而确定出符合要求的答案(一个、多个或所有答案)或探索出解决问题的多种方法．由于开放探究型问题对考查学生思维能力和创造能力有积极的作用，是近几年中考命题的一个热点．通常这类题目有以下几种类型：条件开放与探索，结论开放和探索，条件与结论都开放与探索及方案设计、命题组合型、问题开放型等．【方法点拨】由于开放探究型试题的知识覆盖面较大，综合性较强，灵活选择方法的要求较高，再加上题意新颖，构思精巧，具有相当的深度和难度，所以要求同学们在复习时，首先对于基础知识一定要复习全面，并力求扎实牢靠；其次是要加强对解答这类试题的练习，注意各知识点之间的因果联系，选择合适的解题途径完成最后的解答．由于题型新颖、综合性强、结构独特等，此类问题的一般解题思路并无固定模式或套路，但是可以从以下几个角度考虑：1．利用特殊值（特殊点、特殊数量、特殊线段、特殊位置等）进行归纳、概括，从特殊到一般，从而得出规律．2．反演推理法（反证法），即假设结论成立,根据假设进行推理，看是推导出矛盾还是能与已知条件一致．3．分类讨论法．当命题的题设和结论不唯一确定，难以统一解答时，则需要按可能出现的情况做到既不重复也不遗漏，分门别类加以讨论求解，将不同结论综合归纳得出正确结果．4．类比猜想法．即由一个问题的结论或解决方法类比猜想出另一个类似问题的结论或解决方法，并加以严密的论证．以上所述并不能全面概括此类命题的解题策略，因而具体操作时，应更注重数学思想方法的综合运用．【典型例题】类型一、探索规律1．（2020•武汉校级二模）如图，△ABC面积为1，第一次操作：分别延长AB，BC，CA至点A1，B1，C1，使A1B=AB，C1B=CB，C1A=CA，顺次连接A1，B1，C1，得到△A1B1C1．第二次操作：分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连接A2，B2，C2，得到△A2B2C2，…按此规律，要使得到的三角形的面积超过2020，最少经过（）次操作．A．7 B．6 C．5 D．4【思路点拨】先根据已知条件求出△A1B1C1及△A2B2C2的面积，再根据两三角形的倍数关系求解即可．【答案】D.【解析】解：△ABC与△A1BB1底相等（AB=A1B），高为1：2（BB1=2BC），故面积比为1：2，∵△ABC面积为1，∴S△A1B1B=2．同理可得，S△C1B1C=2，S△AA1C=2，∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7；同理可证△A2B2C2的面积=7×△A1B1C1的面积=49，第三次操作后的面积为7×49=343，第四次操作后的面积为7×343=2401．故按此规律，要使得到的三角形的面积超过2020，最少经过4次操作．故选D．【总结升华】考查了三角形的面积，此题属规律性题目，解答此题的关键是找出相邻两次操作之间三角形面积的关系，再根据此规律求解即可．举一反三：【变式】（2020•抚顺）如图，△A1A2A3，△A4A5A5，△A7A8A9，…，△A3n﹣2A3n﹣1A3n（n为正整数）均为等边三角形，它们的边长依次为2，4，6，…，2n，顶点A3，A6，A9，…，A3n均在y轴上，点O是所有等边三角形的中心，则点A2020的坐标为 .【答案与解析】解：∵△A1A2A3为等边三角形，边长为2，点A3，A6，A9，…，A3n均在y轴上，点O是所有等边三角形的中心，∴A3的坐标为（0，3），∵2020÷3=672，∴A2020是第672个等边三角形的第3个顶点，∴点A2020的坐标为（0，×3），即点A2020的坐标为（0，4483）；故答案为：（0，4483）．类型二、条件开放型、结论开放型2．在平面直角坐标系中，等腰三角形ABC的顶点A的坐标为（2，2）．（1）若底边BC在x轴上，请写出一组满足条件的点B、点C的坐标：；（2）若底边BC的两端点分别在x轴、y轴上，请写出一组满足条件的点B、点C的坐标： .【思路点拨】（1）首先由BC在x轴上，在等腰△ABC中，即可过顶点A作AD⊥BC交BC于D，根据三线合一的性质，可得BD=CD，即B，C关于点D对称，则可求得满足条件的点B、点C的坐标；（2）连接OA，由等腰三角形ABC的顶点A的坐标为（2，2），易证得△AOB≌△AOC，则可知OB=OC，继而可得满足条件的点B、点C的坐标．【答案与解析】解：（1）∵BC在x轴上，在等腰△ABC中，过顶点A作AD⊥BC交BC于D，∵顶点A的坐标为（2，2），∴D的坐标为（2，0），在等腰△ABC中，有BD=CD，∴B，C关于点D对称，∴一组满足条件的点B、点C的坐标为：B（0，0），C（4，0）；（2）连接OA，∵等腰三角形ABC的顶点A的坐标为（2，2），∴∠AOC=∠AOB=45°，∴当OB=OC时，在△AOB与△AOC中，OB=OCAOB=AOC OA=OA⎧⎪∠∠⎨⎪⎩∴△AOB≌△AOC，∴AB=AC，即△ABC是等腰三角形，∴一组满足条件的点B、点C的坐标：（0，1），（1，0）．【总结升华】此题考查了等腰三角形的性质，全等三角形的判定与性质等知识．此题难度适中，解题的关键是注意数形结合思想的应用，注意辅助线的作法．举一反三：【变式】在平面直角坐标系中，等腰三角形ABC的顶点A的坐标为(2，2)．(1)若底边BC在x轴上，请写出一组满足条件的点B，点C的坐标：________________；设点B，点C的坐标分别为(m，0)，(n，0)，你认为m，n应满足怎样的条件？(2)若底边BC的两个端点分别在x轴，y轴上，请写出一组满足条件的点B，点C的坐标：______________；设点B，点C的坐标分别为(m，0)，(0，n)，你认为m，n应满足怎样的条件?【答案】解：可以通过等腰三角形的作法来探求符合题意的条件：由于AB＝AC，故点B和点C在以A为圆心的同一个圆上．(1)如图(a)，作AE⊥x轴于E，以大于AE的长度为半径画弧，与x轴的交点即为符合题意的点B和点C．易知E(2，0)为线段BC的中点，故CE＝EB，即n－2＝2－m；如：点B(0，0)，点C(4，0)；m+n＝4且m ≠n．(2)类似于(1)作OA，与两条坐标轴分别交于B1，B2，C1，C2，显然当A，B，C三点不共线时这样确定的点B，C均符合题意．如：点B(1，0)，点C(0，1)，或点B(3，0)，点C(0，1)；m＝n，且m，n不为0和4；或m+n＝4．类型三、条件和结论都开放的问题3．如图(1)，四边形ABCD中，AD与BC不平行，现给出三个条件：①∠CAB＝∠DBA，②AC＝BD，③AD＝BC．请你从上述三个条件中选择两个条件，使得加上这两个条件后能够推出ABCD是等腰梯形，并加以证明(只需证明一种情况)．【思路点拨】有两种方法，第一种是：①∠CAB=∠DBA，②AC=BD；第二种是：②AC=BD，③AD=BC，均可利用等腰梯形的判定方法进行验证．【答案与解析】解：第一种选择：①∠CAB＝∠DBA，②AC＝BD．证明：由△ACB≌△BDA，可得AD＝BC，∠ABC＝∠BAD．如图(2)作DE∥BC交AB于点E，则∠DEA＝∠CBA．∴∠DAE＝∠DEA，AD＝ED＝BC．由ED＝BC及DE∥BC知，四边形DEBC是平行四边形，所以AB∥CD．∵ AD与．BC不平行，∴四边形ABCD是等腰梯形．第二种选择：②AC＝BD，③AD＝BC．证明：如图(3)，延长AD、BC相交于点E．由△DAB≌△CBA，可得∠DAB＝∠CBA，∴EA＝EB．由AD＝BC，可得DE＝CE，∠EDC＝∠ECD．再由三角形内角和定理可得∠EDC＝∠EAB，∴DC∥AB．∵AD与BC不平行，∴四边形ABCD是等腰梯形．【总结升华】此题一道开放性的题目，主要考查学生对等腰梯形的判定的掌握情况．举一反三：【高清课堂：创新、开放与探究型问题例3】【变式】如图，ABCD是一张矩形纸片，AD=BC=1,AB=CD=5．在矩形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK．（1）若∠1=70°，求∠MNK的度数．（2）△MNK的面积能否小于12？若能，求出此时∠1的度数；若不能，试说明理由．（3）如何折叠能够使△MNK的面积最大？请你利用备用图探究可能出现的情况，求出最大值．（备用图）【答案】解：（1）∵ABCD是矩形，∴AM∥DN．∴∠KNM=∠1．∵∠1=70°，∴∠KNM=∠KMN=70°．（2）不能．过M点作ME⊥DN，垂足为E，则ME=AD=1．∵∠KNM=∠KMN，∴MK=NK，又MK≥ME，∴NK≥1．∴△MNK的面积=NK•ME≥．∴△MNK的面积不可能小于．（3）分两种情况：情况一：将矩形纸片对折，使点B与D重合，此时点K也与D重合．MK=MD=x，则AM=5﹣x．由勾股定理得12+（5﹣x）2=x2，解得x=2.6．∴MD=ND=2.6．S△MNK=S△MND==1.3．情况二：将矩形纸片沿对角线AC对折，此时折痕即为AC．MK=AK=CK=x，则DK=5-x．同理可得MK=NK=2.6．∵MD=1∴S△MNK=S△MND==1.3．△MNK的面积最大值为1.3．类型四、动态探究型4．如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F．另一边交CB的延长线于点G．（1）求证：EF=EG；（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：（3）如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB=a、BC=b，求EFEG的值．【思路点拨】（1）由∠GEB+∠BEF=90°，∠DEF+∠BEF=90°，可得∠DEF=∠GEB，又由正方形的性质，可利用SAS证得Rt△FED≌Rt△GEB，则问题得证；（2）首先点E分别作BC、CD的垂线，垂足分别为H、I，然后利用SAS证得Rt△FEI≌Rt△GEH，则问题得证；（3）首先过点E分别作BC、CD的垂线，垂足分别为M、N，易证EM∥AB，EN∥AD，则可证得△CEN∽△CAD，△CEM∽△CAB，又由有两角对应相等的三角形相似，证得△GME∽△FNE，根据相似三角形的对应边成比例，即可求得答案．【答案与解析】解：（1）证明：∵∠GEB+∠BEF=90°，∠DEF+∠BEF=90°，∴∠DEF=∠GEB，又∵ED=BE，∴Rt △FED ≌Rt △GEB ， ∴EF=EG ；（2）成立．证明：如图，过点E 分别作BC 、CD 的垂线，垂足分别为H 、I ，则EH=EI ，∠HEI =90°，∵∠GEH+∠HEF=90°，∠IEF+∠HEF =90°， ∴∠IEF=∠GEH ， ∴Rt △FEI ≌Rt △GEH ， ∴EF=EG ；（3）解：如图，过点E 分别作BC 、CD 的垂线，垂足分别为M 、N ，则∠MEN=90°， ∴EM ∥AB ，EN ∥AD ．∴△CEN ∽△CAD ，△CEM ∽△CAB ，∴,NE CE EM CEAD CA AB CA ==， ∴NE EM AD AB =，即NE AD b EM AB a==， ∵∠IEF+∠FEM=∠GEM+∠FEM=90°， ∴∠GEM=∠FEN ， ∵∠GME=∠FNE=90°， ∴△GME ∽△FNE ，∴EF ENEG EM =， ∴EF bEG a=． 【总结升华】此题考查了正方形、矩形的性质，以及全等三角形与相似三角形的判定与性质．此题综合性较强，注意数形结合思想的应用．举一反三：【变式1】已知：如图(a)，在Rt△ACB中，∠C＝90°，AC＝4cm，BC＝3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm／s；连接PQ．若设运动的时间为t(s)(0＜t＜2)，解答下列问题：(1)当t为何值时，PQ∥BC?(2)设△AQP的面积为y(cm2)，求y与t之间的函数关系式；(3)是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t 的值．若不存在，说明理由；(4)如图(b)，连接PC，并把△POC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．【答案】解：(1)在Rt△ABC中，AB＝5．由题意知AP＝5-t，AQ＝2t．若PQ∥BC，则△APQ∽△ABC．∴AQ AP AC AB=．∴2545t t-=．解得107t=．(2)过点P作PH⊥AC于H，如图(c)．∵△APH∽△ABC，∴PH AP BC AB=．∴535PH t-=．解得335PH t=-．∴211132(3)32255y AQ PH t t t t =⨯⨯=⨯⨯-=-+． (3)若PQ 把△ABC 周长平分，则AP+AQ ＝BP+BC+CQ ．∴(5-t)+2t ＝t+3+(4-2t)． 解得t ＝1．若PQ 把△ABC 面积平分， 则12APQ ABC S S =△△，即23335t t -+=． ∵t ＝1代入上述方程不成立，∴不存在这一时刻t ，使线段PQ 把Rt △ACB 的周长和面积同时平分． (4)过点P 作PM ⊥AC 于M ，PN ⊥BC 于N ，如图(d)． 若四边形PQP ′C 是菱形，那么PQ ＝PC ． ∵PM ⊥AC 于M ，∴QM ＝CM ．∵PN ⊥BC 于N ，易知△PBN ∽△ABC ．∴PN BP AC AB =，∴45PN t=．解得45tPN =．∴QM ＝CM ＝45t．∴442455t t t ++=． 解得109t =．∴当109t =时，四边形PQP ′C 是菱形．此时37353PM t =-=，4859CM t ==．在Rt △PMC 中，PC ===∴菱形PQP ′C ． 举一反三：【高清课堂：创新、开放与探究型问题 例4】【变式2】如图，点D ，E 在△ABC 的边BC 上，连接AD ，AE. ①AB＝AC ；②AD＝AE ；③BD＝CE.以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：①②⇒③；①③⇒②；②③⇒①.（1）以上三个命题是真命题的为（直接作答） ； （2）请选择一个真命题进行证明（先写出所选命题，然后证明）.【答案】 解：（1）三个都是真命题；（2）解法一 ①②⇒③如图,过点A 作AD ⊥BC 于点F . ∵AB ＝AC , ∴BF ＝CF . ∵AD ＝AE , ∴DF ＝EF . ∴BD ＝CE .解法二 ①③⇒②∵AB ＝AC ,∴∠ABD ＝∠ACE . ∵BD ＝CE ,∴△ABD ≌△ACE (SAS ). ∴AD ＝AE .解法三 ②③⇒①∵AD ＝AE ,∴∠ADE ＝∠AED , 即∠ADB ＝∠AEC ∵BD ＝CE ,∴△ABD ≌△ACE (SAS ). ∴AB ＝AC类型五、创新型5．先阅读下列材料，然后解答问题：从A B C ，，三张卡片中选两张，有三种不同选法，抽象成数学问题就是从3个元素中选取2个元素组合，记作2332C 321⨯==⨯．一般地，从m 个元素中选取n 个元素组合，记作：E DCB A(1)(1)C (1)321n m m m m n n n --+=-⨯⨯⨯例从7个元素中选5个元素，共有5776543C 2154321⨯⨯⨯⨯==⨯⨯⨯⨯种不同的选法．问题：从某学习小组10人中选取3人参加活动，不同的选法共有 种． 【思路点拨】本题需要学生读懂m 个元素中选取n 个元素的计算规则，然后针对具体的从10人中选取3人参加的计算．【答案与解析】由给出的公式可知从10个人中取3个人参加活动，有3101098C 120321⨯⨯==⨯⨯种不同的选法．【总结升华】本题构思精妙、情境新颖.从试题的情境来看，本题以初中数学中的整数的乘除运算等基本运算为素材，以高中数学中组合数的定义及其计算公式为背景，展示给学生的是一个全新的问题，试题具有较大的自由度和思维空间，考查了阅读理解、知识迁移等多种数学能力，体现了主动探究精神，呈现出研究性学习的特点，从而进一步考查了学生自学高中数学知识的能力．从试题的解答来看，直接以组合数的定义及其计算公式为背景的试题在各种复习资料和模拟试题中从未见过，解决这个问题没有现成的“套路”和“招式”，需要学生自主学习组合数的定义及其计算公式的定义，综合运用多种数学思想方法，才能解决问题．中考冲刺：创新、开放与探究型问题—巩固练习（提高）【巩固练习】 一、选择题1.（2020•重庆校级二模）下列图形都是由同样大小的小圆圈按一定规律组成的，其中第①个图形中一共有1个空心小圆圈，第②个图形中一共有6个空心小圆圈，第③个图形中一共有13个空心小圆圈，…，按此规律排列，则第⑦个图形中空心圆圈的个数为（ ）A．61 B．63 C．76 D．782．如图，直角三角形纸片ABC中，AB=3，AC=4，D为斜边BC中点，第1次将纸片折叠，使点A与点D 重合，折痕与AD交与点P1；设P1D的中点为D1，第2次将纸片折叠，使点A与点D1重合，折痕与AD交于点P2；设P2D1的中点为D2，第3次将纸片折叠，使点A与点D2重合，折痕与AD交于点P3；…；设P n﹣1D n﹣2的中点为D n﹣1，第n次将纸片折叠，使点A与点D n﹣1重合，折痕与AD交于点P n（n＞2），则AP6的长为（）A．512532⨯B．69352⨯C．614532⨯D．711352⨯3．下面两个多位数1248624…、6248624…，都是按照如下方法得到的：将第一位数字乘以2，若积为一位数，将其写在第2位上，若积为两位数，则将其个位数字写在第2位．对第2位数字再进行如上操作得到第3位数字……，后面的每一位数字都是由前一位数字进行如上操作得到的．当第1位数字是3时，仍按如上操作得到一个多位数，则这个多位数前100位的所有数字之和是( ) A．495 B．497 C．501 D．503二、填空题4.（2020•合肥校级三模）如图，一个3×2的矩形（即长为3，宽为2）可以用两种不同方式分割成3或6个边长是正整数的小正方形，即：小正方形的个数最多是6个，最少是3个．（1）一个5×2的矩形用不同的方式分割后，小正方形的个数可以是个，最少是个；（2）一个7×2的矩形用不同的方式分割后，小正方形的个数最多是个，最少是个；（3）一个（2n+1）×2的矩形用不同的方式分割后，小正方形的个数最多是个；最少是个．（n 是正整数）5. 一园林设计师要使用长度为4L的材料建造如图1所示的花圃，该花圃是由四个形状、大小完全一样的扇环面组成，每个扇环面如图2所示，它是以点O为圆心的两个同心圆弧和延长后通过O点的两条直线段围成，为使得绿化效果最佳，还须使得扇环面积最大．(1)使图①花圃面积为最大时R －r 的值为 ，以及此时花圃面积为 ，其中R 、r 分别为大圆和小圆的半径；(2)若L ＝160 m ，r ＝10 m ，使图面积为最大时的θ值为 ．6．如图所示，已知△ABC 的面积1ABC S =△，在图(a)中，若11112AA BB CC AB BC CA ===，则11114A B C S =△； 在图(b)中，若22213AA BB CC AB BC CA ===，则222A B C 13S =△；在图(c)，若33314AA BB CC AB BC CA ===，则333716A B C S =△．…按此规律，若88819AA BB CC AB BC CA ===，则888A B C S =△________．三、解答题7．（2020•丹东模拟）已知，点D 为直线BC 上一动点（点D 不与点B 、C 重合），∠BAC=90°，AB=AC ，∠DAE=90°，AD=AE ，连接CE ．（l ）如图1，当点D 在线段BC 上时，求证：①BD ⊥CE ，②CE=BC ﹣CD ；（2）如图2，当点D 在线段BC 的延长线上时，其他条件不变，请直接写出CE 、BC 、CD 三条线段之间的关系；（3）如图3，当点O 在线段BC 的反向延长线上时，且点A 、E 分别在直线BC 的两侧，点F 是DE 的中点，连接AF 、CF ，其他条件不变，请判断△ACF 的形状，并说明理由．8.如图(a)、(b)、(c)，在△ABC中，分别以AB，AC为边，向△ABC外作正三角形、正四边形、正五边形，BE，CD相交于点O．(1)①如图(a)，求证：△ADC≌△ABE；②探究：图(a)中，∠BOC＝________；图(b)中，∠BOC＝________；图(c)中，∠BOC＝________；(2)如图(d)，已知：AB，AD是以AB为边向△ABC外所作正n边形的一组邻边；AC，AE是以AC为边向△ABC外所作正n边形的一组邻边．BE，CD的延长相交于点O．①猜想：图(d)中，∠BOC＝________________；(用含n的式子表示)②根据图(d)证明你的猜想．9. 如图(a)，梯形ABCD中，AD∥BC，∠ABC＝90°， AD＝9，BC＝12，AB＝a，在线段BC上任取一点P(P 不与B，C重合)，连接DP，作射线．PE⊥DP，PE与直线AB交于点E．(1)试确定CP＝3时，点E的位置；(2)若设CP＝x(x＞0)，BE＝y(y＞0)，试写出y关于自变量x的函数关系式；(3)若在线段BC上能找到不同的两点P1，P2，使按上述作法得到的点E都与点A重合，试求出此时a的取值范围．10. 点A，B分别是两条平行线m，n上任意两点，在直线n上找一点C，使BC＝k·AB．连接AC，在直线AC上任取一点E，作∠BEF＝∠ABC，EF交直线m于点F．(1)如图(a)，当k＝1时，探究线段EF与EB的关系，并加以说明；说明：①如果你经过反复探索没有解决问题，请写出探索过程(要求至少写三步)；②在完成①之后，可以自己添加条件(添加的条件限定为∠ABC为特殊角)，在图(b)中补全图形，完成证明．(2)如图(c)，若∠ABC＝90°，k≠l，探究线段EF与EB的关系，并说明理由．【答案与解析】一、选择题1.【答案】A；【解析】∵第①个图形中空心小圆圈个数为：4×1﹣3+1×0=1个；第②个图形中空心小圆圈个数为：4×2﹣4+2×1=6个；第③个图形中空心小圆圈个数为：4×3﹣5+3×2=13个；…∴第⑦个图形中空心圆圈的个数为：4×7﹣9+7×6=61个；2.【答案】A；【解析】由题意得，AD=12BC=52，AD1=AD﹣DD1=158，AD2=25532⨯，AD3=37532⨯，AD n=21532nn+⨯，故AP 1=54，AP 2=1516，AP 3=26532⨯…APn=12532n n-⨯， 故可得AP 6=512532⨯.故选A.3.【答案】A ；【解析】根据题意，当第1位数字是3时，按操作要求得到的数字是3624862486248…，从第2位数字起每隔四位数重复一次6248，因为(100-1)被4整除得24余3，所以这个多位数前100位的所有数字之间和是3+(6+2+4)+(6+2+4+8)×24＝495，答案选A ． 二、填空题 4.【答案】（1）4；10；（2）5；14；（3）4n+2；n+2．【解析】 （1）一个5×2的矩形最少可分成4个正方形，最多可分成10个正方形； （2）一个7×2的矩形最少可分成5个正方形，最多可分成14个正方形；（3）第一个图形：是一个3×2的矩形，最少可分成1+2个正方形，最多可分成1×4+2个正方形； 第二个图形：是一个5×2的矩形，最少可分成2+2个正方形，最多可分成2×4+2个正方形； 第三个图形：是一个7×2的矩形，最少可分成3+2个正方形，最多可分成3×4+2个正方形； …第n 个图形：是一个（2n+1）×2的矩形，最多可分成n ×4+2=4n+2个正方形，最少可分成n+2个正方形． 故答案为：（1）4；10；（2）5；14；（3）4n+2；n+2．5.【答案】（1）R －r 的值为4L ，以及此时花圃面积为24L ； （2）θ值为240π．【解析】要使花圃面积最大，则必定要求扇环面积最大．设扇环的圆心角为θ，面积为S ，根据题意得：2()180180R rL R r θπθπ=++- ()2()180R r R r πθ+=+-，∴180[2()]()L R r R r θπ--=+∴2222()360360360R r S R r θπθππθ=-=-22180[2()]()360()L R r R r R r ππ--=-+1[2()]()2L R r R r =--- 21()()2R r L R r =--+-22()416L L R r ⎡⎤=---+⎢⎥⎣⎦．∵02L R r <-<， ∴S 在4LR r -=时取最大值为216L ．∴花圃面积最大时R －r 的值为4L，最大面积为224164L L ⨯=．(2)∵当4LR r -=时，S 取大值， ∴1604044L R r -===(m)，40401050R r =+=+=(m)，∴180[2()]180(160240)240()60L R r R r θπππ---⨯===+．6.【答案】1927． 【解析】3331-3=4416A B C S =⨯⨯△…三、解答题 7．【答案与解析】（1）证明：如图1中，∵∠BAC=∠DAE=90°，∴∠BAD=∠CAE ， 在△ABD 和△ACE 中，，∴△ABD≌△ACE，∴∠ABD=∠ACE=45°，BD=CE，∴∠ACB+∠ACE=90°∴∠ECB=90°，∴BD⊥CE，CE=BC﹣CD．（2）如图2中，结论：CE=BC+CD，理由如下：∵∠BAC=∠DAE=90°，∴∠BAD=∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE，∴BD=CE，∴CE=BC+CD．（3）如图3中，结论：△ACF是等腰三角形．理由如下：∵∠BAC=∠DAE=90°，∴∠BAD=∠CAE，在△ABD和△ACE中，∴△ABD≌△ACE，∴∠ABD=∠ACE，∵∠ABC=∠ACB=45°，∴∠ACE=∠ABD=135°，∴∠DCE=90°，又∵点F是DE中点，∴AF=CF=DE，∴△ACF是等腰三角形．8．【答案与解析】(1)证法一：∵△ABD与△ACE均为等边三角形，∴AD＝AB，AC＝AE，且∠BAD＝∠CAE＝60°．∴∠BAD+∠BAC＝∠CAE+∠BAC，即∠DAC＝∠BAE．∴△ADC≌△ABE．证法二：∵△ABD与△ACE均为等边三角形，∴AD＝AB，AC＝AE，且∠BAD＝∠CAE＝60°．∴△ADC可由△ABE绕着点A按顺时针方向旋转60°得到．∴△ABE≌△ADC．②120°，90°，72°．(2)①360n°．②证法一：依题意，知∠BAD和∠CAE都是正n边形的内角，AB＝AD，AE＝AC，∴∠BAD＝∠CAE＝(2)180nn-°．∴∠BAD－∠DAE＝∠CAE－∠DAE，即∠BAE＝∠DAC．∴△ABE≌△ADC．∴∠ABE＝∠ADC．∵∠ADC+∠ODA＝180°，∴∠ABO+∠ODA＝180°．∴∠ABO+∠ODA+∠DAB+∠BOC＝360°．∴∠BOC+∠DAB＝180°．∴∠BOC＝180°－∠DAB＝(2)180360 180nn n--=°°°．证法二：延长BA交CO于F，证∠BOC＝∠DAF＝180°-∠BAD．证法三：连接CE．证∠BOC＝180°－∠CAE．9．【答案与解析】解：(1)作DF⊥BC，F为垂足．当CP＝3时，四边形ADFB是矩形，则CF＝3．∴点P与点F重合．又∵BF⊥FD，∴此时点E与点B重合．(2)(i)当点P 在BF 上(不与B ，F 重合)时，(见图(a))∵∠EPB+∠DPF ＝90°，∠EPB+∠PEB ＝90°，∴∠DPF ＝∠PEB ．∴Rt △PEB ∽△ARt △DPF ． ∴BE FP BP FD=． ① 又∵ BE ＝y ，BP ＝12-x ，FP ＝x-3，FD ＝a ，代入①式，得312y x x a-=- ∴1(12)(3)y x x a=--，整理， 得21(1536)(312)y x x x a =-+<< ② (ii)当点P 在CF 上（不与C ，F 重合）时，（见上图(b))同理可求得BE FP BP FD =． 由FP ＝3-x 得21(1536)(03)y x x x a=-+<<． ∴ 221(1536)(03)1(1536)(312).x x x a y x x a⎧--+<<⎪⎪=⎨⎪--+<<⎪⎩ (3)解法一：当点E 与A 重合时，y ＝EB ＝a ，此时点P 在线段BF 上． 由②式得21(1536)a x x a =--+． 整理得2215360x x a -++=． ③∵在线段BC 上能找到两个不同的点P 1与P 2满足条件，∴方程③有两个不相等的正实根．∴△＝(-15)2－4×(36+a 2)＞0．解得2814a <． 又∵a ＞0， ∴902a <<． 解法二：当点E 与A 重合时，∵∠APD ＝90°，∴点P 在以AD 为直径的圆上．设圆心为M ，则M 为AD 的中点． ∵在线段BC 上能找到两个不同的点P 1与P 2满足条件，∴线段BC 与⊙M 相交．即圆心M 到BC 的距离d 满足02AD d <<． ④ 又∵AD ∥BC ，∴d ＝a ． ∴由④式得902a <<．10．【答案与解析】解：(1)EF＝EB．证明：如图(d)，以E为圆心，EA为半径画弧交直线m于点M，连接EM．∴EM＝EA，∴∠EMA＝∠EAM．∵BC＝k·AB，k＝1，∴BC＝AB．∴∠CAB＝∠ACB．∵m∥n，∴∠MAC＝∠ACB，∠FAB＝∠ABC．∴∠MAC＝∠CAB．∴∠CAB＝∠EMA．∵∠BEF＝∠ABC，∴∠BEF＝∠FAB．∵∠AHF＝∠EHB，∴∠AFE＝∠ABE．∴△AEB≌△MEF．∴EF＝EB．探索思路：如上图(a)，∵BC＝k·AB，k＝1，∴BC＝AB．∴∠CAB＝∠ACB．∵m∥n，∴∠MAC＝∠ACB．添加条件：∠ABC＝90°．证明：如图(e)，在直线m上截取AM＝AB，连接ME．∵ BC＝k·AB，k＝1，∴ BC＝AB．∵∠ABC＝90°，∴∠CAB＝∠ACB＝45°．∵ m∥n，∴∠MAE＝∠ACB＝∠CAB＝45°，∠FAB＝90°．∵ AE＝AE，∴△MAE∽△BAE．∴ EM＝EB，∠AME＝∠ABE．∵∠BEF＝∠ABC＝90°，∴∠FAB+∠BEF＝180°．又∵∠ABE+∠EFA＝180°，∴∠EMF＝∠EFA．∴ EM＝EF．∴ EF＝EB．(2)EF＝1k EB．说明：如图(f)，过点E作EM⊥m，EN⊥AB，垂足为M，N．∴∠EMF＝∠ENA＝∠ENB＝90°．∵ m∥n，∠ABC＝90°，∴∠MAB＝90°．∴四边形MENA为矩形．∴ ME＝NA，∠MEN＝90°．∵∠BEF＝∠ABC＝90°．∴∠MEF＝∠NEB．∴△MEF∽△NEB．∴ME EF EN EB=，∴AN EF EN EB=在Rt△ANE和Rt△ABC中，tanEN BCBAC kAN AB∠===，∴1EF EBk=．。

搭建支架深度学习作者：施与颀来源：《作文成功之路·中考冲刺》2020年第10期20世纪70年代美国著名教育家、心理学家布鲁纳，在苏联心理学家维果斯基的“最近发展区”理论基础上，提出了“支架式教学”这一概念。

“支架”在教学中可以理解为教师为了让学生进一步理解新知识，而提供的一种起辅助与支撑作用的概念框架。

在基于“知识与技能”“过程与方法”“情感态度与价值观”三维目标的小学阅读教学中，教师根据具体的教学目标，构建合适的支架，就能让学生自主探索，深入思考，解决问题，提高素养。

教学支架的种类和形式多种多样，本文选择4个较为实用的支架进行阐述分析。

一、巧设问题式支架，抛砖引玉提问是教学的重要环节，教师在钻研教材、认真分析学情的基础上，巧设问题式支架，能够为学生指明独立思考、解决问题的方向。

请看《什么比猎豹的速度更快》教学片段：师：作者介绍了八种事物的速度一个比一个快，却丝毫不令我们感到枯燥单调，是因为他或直接引出类比的事物，或巧妙运用卖关子的写作方式，把我们带入神奇的世界，让我们越读越想读。

生：全体朗读。

师：既然卖关子能激发读者的阅读兴趣，那么作者是不是每一次的过渡都在卖关子呢？生：全文有三次过渡直接点出了说明的事物——“比鸵鸟跑得更快的动物就要数猎豹了。

”“但是游隼向下俯冲时的速度更快。

”“不过，游隼还是没有飞机飞行的速度快。

”师：那为什么不每次过渡都卖关子呢？生：每次都卖关子就太啰唆了。

况且前面几种事物都是我们生活中常见的，也不需要卖关子。

师：是的，这告诉我们即使是介绍科学知识的文章，也要注意写法的多样性，行文富于变化才能吸引读者。

教师以“巧卖关子”构建问题式支架，通过问题启发学生思考，让学生亲身经历探索、发现、习得的过程，培养学生的自主学习能力。

问题式支架虽妙但过犹不及，过多的问题式支架往往会割裂课堂，给人一种零碎感。

教师应结合文本特点、教学重难点，整体把握文本，设计聚焦文本核心的主问题式支架，引导学生运用高阶思维，深度学习，解决问题。