(优选)离散数学第五版第九章.Ppt
- 格式:ppt
- 大小:811.00 KB
- 文档页数:82

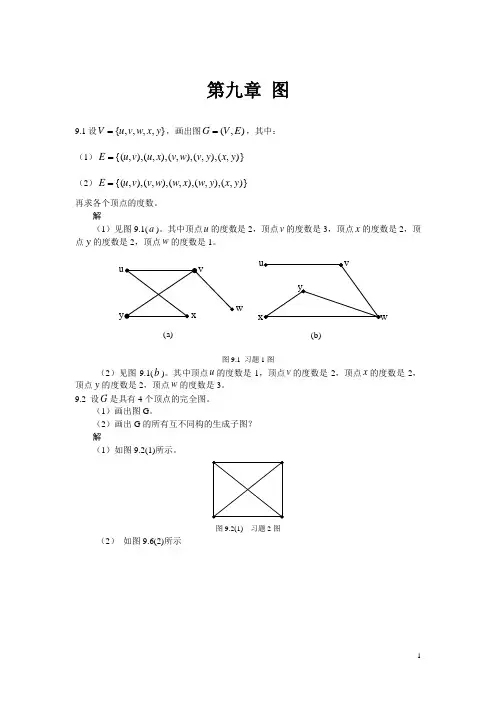
第九章 图9.1设},,,,{y x w v u V =,画出图),(E V G =,其中:(1))},(),,(),,(),,(),,{(y x y v w v x u v u E =(2))},(),,(),,(),,(),,{(y x y w x w w v v u E =再求各个顶点的度数。
解(1)见图9.1(a )。
其中顶点u 的度数是2,顶点v 的度数是3,顶点x 的度数是2,顶点y 的度数是2,顶点w 的度数是1。
图9.1 习题1图(2)见图9.1(b )。
其中顶点u 的度数是1,顶点v 的度数是2,顶点x 的度数是2,顶点y的度数是2,顶点w 的度数是3。
9.2 设G 是具有4个顶点的完全图。
(1)画出图G 。
(2)画出G 的所有互不同构的生成子图?解(1)如图9.2(1)所示。
图9.2(1) 习题2图(2) 如图9.6(2)所示﹒ ﹒ ﹒ ﹒ ﹒ ﹒图9.2(2) 习题2图9.3 一个无向简单图,如果同构于它的补图,则称这个图为自互补图。
(1)试画出五个顶点的自互补图。
(2)证明一个自互补图一定只有k 4或14+k 个顶点(k 为整数)。
解(1)(a) (b)图9.3 习题3图 (2)因为n 个顶点的无向完全图有)1(21-n n 条边,所以自互补图有)1(41-n n 条边,因此,k n 4=或14+k 。
9.4 画出两个不同构的简单无向图。
每一个图都仅有6个顶点,且每个顶点都均是3度,并指出这两个图为什么不同构。
解图9.4 习题9.4图9.5 证明任意两个同构的无向图,一定有一个同样的顶点度序列。
顶点度序列是一组按大小排列的正整数。
每一个数对应某一个顶点的度数。
证明两个同构的无向图,度数相同的顶点数目一定相同,这样才能够建立起顶点之间的一一对应关系,进而建立起边的对应关系。
所以,任意二个同构的无向图,一定有一个同样的顶点度序列。
9.6图9.6中所给的图(a )与图(b )是否同构?为什么?(a )(b ) 图9.6 习题6图 解左图9.2(a )中次数为4的点,与3个度数为1,一个度数为2的顶点相邻接,右图9.2(b )中度数为4的点,却与3个度数为1,一个度数为3的顶点相邻接。








