可能性(概率)-Probability
- 格式:ppt
- 大小:1.30 MB
- 文档页数:51

数学名词解释数学是一门研究数量、结构、空间以及变化的学科,其中包含了大量的专业术语和概念。
在本文中,将解释一些常见的数学名词,帮助读者更好地理解数学领域各个方面。
1. 整数(integer):整数是没有小数部分的数字,可以是正数、负数或零。
整数在数学中非常重要,常用于计数、排序等。
例如:-3、0、5。
2. 分数(fraction):分数是用两个整数表示的有理数,一个表示分子,另一个表示分母。
分数可以表示部分或比例。
例如:1/2、3/4。
3. 百分比(percentage):百分比指的是以100为基准的比例表示法,常用符号“%”表示。
百分比在描述比较和统计数据时很常见。
例如:50%表示50的一半。
4. 方程(equation):方程是等式的一种形式,其中包含了一个或多个未知数。
通过解方程,可以找到未知数的值。
例如:2x + 3 = 7是一个简单的一元一次方程。
5. 函数(function):函数是一种将一个集合的元素映射到另一个集合的关系。
函数通常根据一个或多个输入值来计算输出值。
例如:f(x) = 2x是一个简单的线性函数。
6. 导数(derivative):导数是描述函数在某点上变化率的概念,表示函数在该点的斜率。
导数在微积分中有广泛应用。
例如:对于函数f(x) = x^2,其导数为f'(x) = 2x。
7. 积分(integral):积分是对函数的求和操作的逆运算。
通过积分,可以计算出函数下曲线与x轴之间的面积或求得某一区间上的平均值。
例如:∫(2x^2) dx可以表示对函数f(x) = 2x^2的积分。
8. 三角函数(trigonometric function):三角函数是通过三角形中的角度来定义的函数。
常见的三角函数有正弦(sine)、余弦(cosine)和正切(tangent)。
例如:sin(30°)表示30度角的正弦值。
9. 矩阵(matrix):矩阵是由数字按照规则排列而成的矩形数组。


1. 总体(population):根据研究目的所确定的同质观察单位的全体。
只包括(确定的时间和空间范围内)有限个观察单位的总体,称为有限总体(finite population)。
假想的,无时间和空间概念的,称为无限总体(infinite population)。
2. (总体)参数(parameter):总体的统计指标或特征值。
总体参数是事物本身固有的、不变的。
3. 样本(sample):从总体中随机抽取的部分个体。
4. 样本含量(sample size):样本中所包含的个体数。
5. 变量(variable):观察对象个体的特征或测量的结果。
由于个体的特征或指标存在个体差异,观察结果在测量前不能准确预测,故称为随机变量(random variable),简称变量(variable)。
变量的取值称为变量值或观察值(observation)。
根据变量的取值特性,分为数值变量和分类变量。
6. 数值变量(Numerical variable):又称为计量资料、定量资料,指构成其的变量值是定量的,其表现为数值大小,有单位。
对每个观察单位用定量的方法测定某项指标的数值,组成的资料。
7. 计数资料:将全体观测单位按照某种性质或特征分组,然后再分别清点各组观察单位的个数。
分类变量(categorical variable):或称定性变量,其取值是定性的,表现为互不相容的类别或或属性,有两种情况:1)无序分类(unordered categories):包括①二项分类,如上述“性别”变量,表现为互相对立的结果;②多项分类,如上述“血型”变量,表现为互不相容的多类结果。
2)有序分类(ordered categories):各类之间有程度上的差别,或等级顺序关系,有“半定量”的意义,亦称等级变量。
等级资料:介于计量资料和计数资料之间的一种资料,通过半定量方法测量得到。
8. 抽样(sampling):从总体中抽取部分观察单位的过程称为抽样。
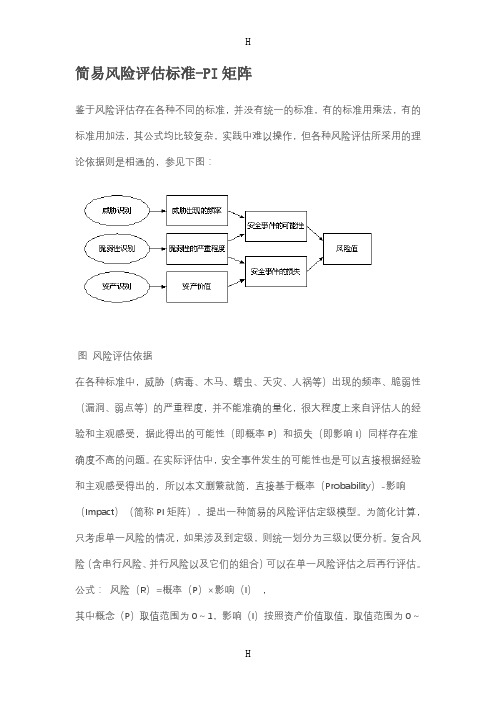
简易风险评估标准-PI矩阵鉴于风险评估存在各种不同的标准,并没有统一的标准,有的标准用乘法,有的标准用加法,其公式均比较复杂,实践中难以操作,但各种风险评估所采用的理论依据则是相通的,参见下图:图风险评估依据在各种标准中,威胁(病毒、木马、蠕虫、天灾、人祸等)出现的频率、脆弱性(漏洞、弱点等)的严重程度,并不能准确的量化,很大程度上来自评估人的经验和主观感受,据此得出的可能性(即概率P)和损失(即影响I)同样存在准确度不高的问题。
在实际评估中,安全事件发生的可能性也是可以直接根据经验和主观感受得出的,所以本文删繁就简,直接基于概率(Probability)-影响(Impact)(简称PI矩阵),提出一种简易的风险评估定级模型。
为简化计算,只考虑单一风险的情况,如果涉及到定级,则统一划分为三级以便分析。
复合风险(含串行风险、并行风险以及它们的组合)可以在单一风险评估之后再行评估。
公式:风险(R)=概率(P)×影响(I),其中概念(P)取值范围为0~1,影响(I)按照资产价值取值,取值范围为0~资产价值。
则风险(R)的取值范围为0~资产价值。
这里我们假设某组织的全部资产价值为1000万,最大的风险是损失全部资产,如果采取平均分级(三级)的办法,那么最小一级的上限也有333万,这仍是一个比较大的数字,明显不符合人们对低损失的心理预期;如果按照指数级数进行分级,分别用10万以内代表低损失,10~100万代表中等损失,100~1000万代表高损失,更接近人们的心理感觉。
用公式表达,风险评估定量评估标准为:低风险:PI<10万中风险:10万<PI<100万高风险:100万<PI<1000万此标准针对不同的组织,应根据其资产规模进行相应的调整。
按照概率(P)为横坐标,影响(I)为纵坐标,绘出曲线图如下:图PI矩阵其中红线代表PI=100,蓝线代表PI=10,把不同的区域涂上色,即:图PI矩阵-风险分布图中,红色区域代表100万<PI<1000万,即高风险区域;黄色代表10万<PI<100万,即中风险区域;绿色区域代表PI<10万,即低风险区域。


probability和possibility区别possibility意思:n.可能;可能性;可选择的方法;机会;契机;probability意思:n.可能性;或然性;很可能发生的事;概率;几率;或然率。
probability和possibility区别一、指代不同1、possibility:可能,可能性。
2、probability:可能性,或然性。
二、用法不同1、possibility:possibility后不能接动词不定式,可接“of sth/ v -ing”结构或that同位语从句。
2、probability:用作名词 (n.)The probability that it will rain today is high.今天下雨的可能性很大。
衡量某一事件发生的可能性的指标;表示有利情况与可能发生的全部情况之比的数字。
三、侧重点不同1、possibility:有发生的可能性。
2、probability:不具有发生的可能性。
probability和possibility的例句There seemed to be a high probability of success.成功的几率似乎很高。
It now seems a probability rather than just a possibility.这件事似乎十拿九稳,而不是仅有可能。
A fall in interest rates is a strong probability in the present economic climate.在目前的经济形势下,降低利率大有可能。
It’s a theoretical possibility.这是理论上存在的可能性。
We cannot discount the possibility of further strikes.我们不能低估再次发生罢工的可能性。
是以概率理论为基础,研究生命科学中随机现象规律性的应用数学科学。
涉及到医学科学研究的设计、资料搜集、归纳、分析与解释的一门应用性基础学科、二、科学研究的基本程序1、提出一个欲待研究的问题:2、科学研究设计:专业设计、统计学设计:究对象,拟定研究因素及其分配,如何执行随机、对照与重复的统计学原则,如何观察与度量效应,以及数据收集、整理与分析的方法,通过合理的、系统的安排,达到控制系统误差,以尽可能少的资源消耗(最小的人力、物力、财力和时间)获取准确可靠的信息资料及可信的结论,使效益最大化。
3、获取试验与观察的资料,又称为搜集资料4、数据审核与计算机录入5、分析资料进行检测与描述。
(confidence interval)估计与统计学假设检验(hypothesis test)。
统计学分析过程按变量的多寡可分为单变量分析与多重变量分析。
6、分析结果的合理解释(Explication of results):研究中应注意的问题1、统计学结论的正确与否取决于统计学分析数据的真实性、准确性以及研究样本对研究总体的代表性。
2、尽可能地控制系统误差是统计分析数据真实性、准确性的保证。
3、随机化抽样是确保样本数据对研究总体具有代表性的重要过程。
,个体的许多属性(如年龄、性别、血浆胆固醇等)存在变异性,统计学上将反映个体简称变量; 针对不同类型的属性,需采用不同类型的变量,因而产生不同类型的资料。
根据研究目的所确定的具有相同性质的观察单位的集合成为总体(母体)。
从同一总体中通过随机化过程抽取的部分观察单位称为样本(子样)。
对照组的过程。
体的参数不等,或多个样本的统计量存在差异性称为抽样误差。
A的发生概率记为P(A)。
概率的取值在0 到1之间,若P=1或P=0的事件称为必然事件,若0<P<1 的事件为随机事件。
概率接近于0(如P<0.05)的事件称为小概率事件。
μ表示总体均数,σ表示总体标准差,π表示总体率。