裂纹尖端应力强度因子的计算.

表面裂纹应力强度因子表面裂纹应力强度因子是研究材料表面裂纹扩展行为的重要参数。

裂纹是材料中的一种缺陷，会导致材料的强度和可靠性下降。

了解和控制表面裂纹的应力强度因子对于预测和改善材料的使用寿命至关重要。

表面裂纹应力强度因子是衡量裂纹尖端附近应力状态的物理量。

它描述了应力场的强度和分布，对于裂纹扩展的驱动力起到决定性作用。

表面裂纹应力强度因子的大小与裂纹尖端处的应力集中程度直接相关。

当应力集中较大时，裂纹的扩展速率也会增加。

表面裂纹应力强度因子的计算通常采用弹性力学理论中的应力分析方法。

它可以通过应力分布和裂纹几何形状来计算得出。

不同的裂纹类型和几何形状将导致不同的应力分布和应力强度因子。

因此，在研究和预测裂纹行为时，需要对裂纹类型和几何形状进行准确的描述和分析。

表面裂纹应力强度因子的大小对于材料的疲劳寿命和断裂韧性具有重要影响。

当裂纹尖端处的应力强度因子达到材料的断裂韧性临界值时，裂纹将会迅速扩展，导致材料的断裂。

因此，研究裂纹的应力强度因子有助于预测材料的断裂行为和寿命。

在实际应用中，通过控制和减小表面裂纹应力强度因子，可以有效地提高材料的强度和可靠性。

一种常用的方法是在材料表面引入压缩应力场，以抵消裂纹尖端处的拉伸应力。

这样可以减小应力集中程度，降低表面裂纹的扩展速率。

通过合理的材料选择和工艺优化，也可以降低表面裂纹应力强度因子。

选择具有高韧性和抗裂纹扩展能力的材料，可以使裂纹的扩展速率减缓并延长材料的使用寿命。

优化加工工艺，避免引入应力集中和表面缺陷，也有助于降低表面裂纹应力强度因子。

表面裂纹应力强度因子是研究材料表面裂纹行为的重要参数。

了解和控制表面裂纹的应力强度因子对于预测和改善材料的使用寿命具有重要意义。

通过合理的材料选择、工艺优化和应力控制，可以有效地降低表面裂纹应力强度因子，提高材料的强度和可靠性。

这将为实际工程中的材料设计和使用提供重要参考。

应力场强度因子
应力场强度因子是研究材料断裂行为的重要参数之一。

它是描述材料在受到外力作用下，裂纹尖端应力场的强度和分布情况的物理量。

应力场强度因子的大小和方向对材料的断裂行为有着重要的影响。

应力场强度因子的计算方法有多种，其中最常用的是Williams和Landel的方法。

该方法基于线弹性力学理论，通过对裂纹尖端应力场的分析，得出了应力场强度因子的计算公式。

该公式中包含了裂纹尖端应力场的强度和分布情况，因此可以用来预测材料的断裂行为。

应力场强度因子的大小和方向对材料的断裂行为有着重要的影响。

当应力场强度因子达到一定的临界值时，裂纹尖端的应力场会达到材料的断裂强度，从而导致材料的断裂。

因此，应力场强度因子可以用来预测材料的断裂强度和断裂模式。

除了预测材料的断裂行为外，应力场强度因子还可以用来优化材料的设计和制备。

通过对应力场强度因子的分析，可以确定材料的最大承载能力和断裂模式，从而优化材料的设计和制备过程。

应力场强度因子是研究材料断裂行为的重要参数之一。

它可以用来预测材料的断裂行为、优化材料的设计和制备过程，对于提高材料的性能和可靠性具有重要的意义。

基于ANSYS的断裂参数的计算本文介绍了断裂参数的计算理论，并使用ANSYS进展了实例计算。

通过计算说明了ANSYS可以用于计算断裂问题并且可以取得很好的计算结果。

1 引言断裂事故在重型机械中是比拟常见的，我国每年因断裂造成的损失十分巨大。

一方面，由于传统的设计是以完整构件的静强度和疲劳强度为依据，并给以较大的安全系数，但是含裂纹在役设备还是常有断裂事故发生。

另一方面，对于一些关键设备，缺乏对不完整构件剩余强度的估算，让其提前退役，从而造成了不必要的浪费。

因此，有必要对含裂纹构件的断裂参量进展评定，如应力强度因了和J积分。

确定应力强度因了的方法较多，典型的有解析法、边界配位法、有限单元法等。

对于工程上常见的受复杂载荷并包含不规如此裂纹的构件，数值模拟分析是解决这些复杂问题的最有效方法。

本文以某一锻件中取出的一维断裂试样为计算模型，介绍了利用有限元软件ANSYS计算应力强度因子。

2 断裂参量数值模拟的理论根底对于线弹性材料裂纹尖端的应力场和应变场可以表述为：其中K是应力强度因子，r和θ是极坐标参量，可参见图1，(1)式可以应用到三个断裂模型的任意一种。

图1 裂纹尖端的极坐标系应力强度因子和能量释放率的关系：G=K/E" (3)其中：G为能量释放率。

平面应变：E"=E/(1-v2)平面应力：E=E"3 求解断裂力学问题断裂分析包括应力分析和计算断裂力学的参数。

应力分析是标准的ANSYS线弹性或非线性弹性问题分析。

因为在裂纹尖端存在高的应力梯度，所以包含裂纹的有限元模型要特别注意存在裂纹的区域。

如图2所示，图中给出了二维和三维裂纹的术语和表示方法。

图2 二维和三维裂纹的结构示意图3.1 裂纹尖端区域的建模裂纹尖端的应力和变形场通常具有很高的梯度值。

场值得准确度取决于材料，几何和其他因素。

为了捕获到迅速变化的应力和变形场，在裂纹尖端区域需要网格细化。

对于线弹性问题，裂纹尖端附近的位移场与成正比，其中r是到裂纹尖端的距离。

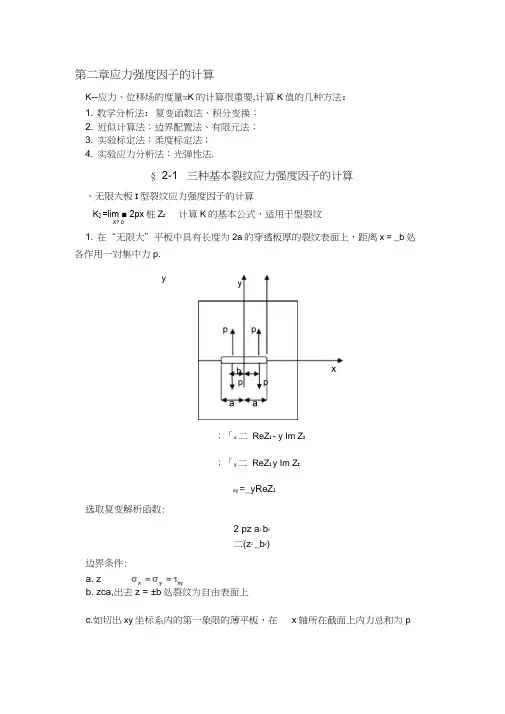
第二章应力强度因子的计算K--应力、位移场的度量=K的计算很重要,计算K值的几种方法：1. 数学分析法：复变函数法、积分变换；2. 近似计算法：边界配置法、有限元法；3. 实验标定法：柔度标定法；4. 实验应力分析法：光弹性法.§ 2-1 三种基本裂纹应力强度因子的计算、无限大板I型裂纹应力强度因子的计算K] =lim ■ 2px桩Z I计算K的基本公式，适用于型裂纹X? 01. 在“无限大”平板中具有长度为2a的穿透板厚的裂纹表面上，距离x = _b处各作用一对集中力p.y；「x 二ReZ i - y Im Z I；「y 二ReZ i y Im Z Ixy =_yReZ l选取复变解析函数:2 pz a2b2二(z2_b2)边界条件:a. zb. zca,出去z = ±b处裂纹为自由表面上c.如切出xy坐标系内的第一象限的薄平板，在x轴所在截面上内力总和为p2 p (匕 +a) Ja 2+孑二[(a)2-b 2] ； (2a)2p 、、 a二(a 2-b 2)2. 在无限大平板中,具有长度为2a 的穿透板厚的裂纹表面上，在距离x= _印的 范围内受均布载荷q 作用.yb.11yqn____ r~Kq 1旺x------ ►J 2 a利用叠加原理：a2q\a i . ---------------- dxo _ / 2 2、二(a -x )令x=acos : a 2-x 2= acosv , dx = acos 二当整个表面受均布载荷时，c -• a. =K i = 2^-s in3. 受二向均布拉力作用的无限大平板，在x 轴上有一系列长度为2a ，间距为2b的裂纹.以新坐标表示:K i微段 > 集中力qdx > dK i2q烏 dx 护(a 2_x 2)-K isin 4(J)广;)竺吗=a cos^二0, -a ::: x ::: a, -a 二2b ：：： x ：：： a 二2b 在区间内；-y =°,，xy =c.所有裂纹前端；匚y.匚单个裂纹时又Z应为2b的周期函数采用新坐标：=z-an ..-sin ( a) 2b当© t 0时,sin 二© =厶Jcos 厶© =12b 2b 2b迟JL乜JL JL乜= sin——( a) =sin—— cos一a cos一sin — a 2b2b 2b 2b 2b边界条件是周期的：a. z —二二xb.在所有裂纹内部应力为零.y~2 2z - a-sin2b二a、2(Sin" %2b 仙2b)JI u 31ji.二 a 二 sin - 2b 1 -a . -a ——cos ——sin — 2b 2b 2b =；「2b tan a \ 2b—a, 2b tan ：aYn a2b2a 1若裂纹间距离比裂纹本身尺寸大很多（兰乞丄）可不考虑相互作用，按单个裂纹2b 5计算•二、无限大平板n>m 型裂纹问题应力强度因子的计算1. u 型裂纹应力强度因子的普遍表达形式（无限大板）:心计吋（人尹2. 无限大平板中的周期性的裂纹，且在无限远的边界上处于平板面内的纯剪切 力作用.JT JT cos a sin a 2b 2b2bfTTfTTfTTfTTHTfTTfTT.. 2 ■22 2[sin (a)] = ( ) cos a 2 cos a sin a (sin a) 2b2b 2b 2b 2b 2b2b•2：:.2[%(a)] -(sin2b a)JI=2 -2bn Jicos asin a2b 2b:二 sin2b—2/ ?.a .二 acos ——sin2b 2b2b 修正系数,大于1,表示其他裂纹存在对K ］的影响.二a 2 药）心=帆 J 2 兀©Z (©) = i V^a J^tan 舒3.川型裂纹应力强度因子的普遍表达形式（无限大板）:4.周期性裂纹:sin二z 2b n ： …sin ( a) 2bZ()二訓n 2?+a)]2-伽訝H Z 2伽亦）一伽§ 2-2 深埋裂纹的应力强度因子的计算1950年，格林和斯内登分析了弹性物体的深埋的椭圆形裂纹邻域内的应力 和应变，得到椭圆表面上任意点，沿y 方向的张开位移为：2 2 1x z . 2 y =y 0（1 2 2）a c2（1 -」2）；「a 其中：yo =（丘丿.-为第二类椭圆积分•有Ji | 2 2=o 2、1-c；asin 2d 「（于仁东书丿匹 a^2 二 2[sin 2「（-）2cos 2] d （王铎书丿 0c1962年,lrwin 利用上述结果计算在这种情况下的应力强度因子xz2 2 2 2 2N 二 Qcos : ,x ,-『sin :2 2 X i 乙-2~~2acacc 2sin 2「a 2cos 2假设：椭圆形裂纹扩展时，其失径「的增值r 与「成正比.边缘上任一点p （x ,z ）,有:x j (「r)sin 炉=(1 f^?sin 》=(1 f)x iz = r)cos 即=(1 f )z 1=■ p (x ；z), p (M,Z i )均在 y=0 的平面内.— ,:2 ・2-2 24 2 2・2 ・2=c x a z (i f)ac a c=新的裂纹面仍为椭圆•长轴c =(i • f)c ,短轴a '=(i • f)a .=y 向位移2 2原有裂纹面：二 二,上）2=ia c y o2 2扩展后裂纹面：笃•务•（工）2=i a c y o以x'x i , z'z,代入=原有裂纹面的边缘y 向位移y ,有原裂纹面y o2(i 」2)二 a2(i-」2)ri f)aE=(i f)y oc 2片2a 2zj 二 a 2c 2sin 2「亠 a 2cos2 :2 2 2 2 2 2「-（1-2门笃一（1一2门刍=1一笃一乌2f （笃吕）ac a ca c=2f二 y 2=2fy °2=2f （1 f ）2y o 2L 2fy 。

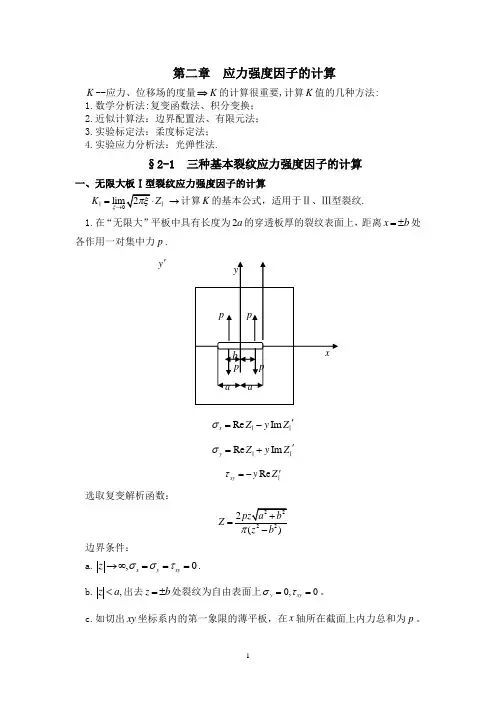
第二章 应力强度因子的计算K --应力、位移场的度量⇒K 的计算很重要,计算K 值的几种方法: 1.数学分析法:复变函数法、积分变换； 2.近似计算法：边界配置法、有限元法； 3.实验标定法：柔度标定法； 4.实验应力分析法：光弹性法.§2-1 三种基本裂纹应力强度因子的计算一、无限大板Ⅰ型裂纹应力强度因子的计算K Z ξ→=→ⅠⅠ计算K 的基本公式，适用于Ⅱ、Ⅲ型裂纹.1.在“无限大”平板中具有长度为2a 的穿透板厚的裂纹表面上，距离x b =±处各作用一对集中力p .Re Im x Z y Z σ'=-ⅠⅠRe Im y Z y Z σ'=+ⅠⅠRe xy y Z τ'=-Ⅰ选取复变解析函数：222()Z z b π=- 边界条件：a.,0x y xy z σστ→∞===.b.,z a <出去z b =±处裂纹为自由表面上0,0y xy στ==。

c.如切出xy 坐标系内的第一象限的薄平板，在x 轴所在截面上内力总和为p 。

y '以新坐标表示：Z=⇒lim()K Zξξ→==Ⅰ2.在无限大平板中,具有长度为2a的穿透板厚的裂纹表面上，在距离1x a=±的范围内受均布载荷q作用.利用叠加原理:微段→集中力qdx→dK=Ⅰ⇒K=⎰Ⅰ令cos cosx a aθθ==,cosdx a dθθ=⇒111sin()1cos22(cosaa aaaK daθθθ--==Ⅰ当整个表面受均布载荷时,1a a→.⇒12()aaK-==Ⅰ3.受二向均布拉力作用的无限大平板,在x轴上有一系列长度为2a,间距为2b 的裂纹.边界条件是周期的: a. ,y x z σσσ→∞==.b.在所有裂纹内部应力为零.0,,22y a x a a b x a b =-<<-±<<±在区间内0,0y xy στ==c.所有裂纹前端y σσ> 单个裂纹时Z =又Z 应为2b 的周期函数⇒sinzZ πσ=采用新坐标:z a ξ=-⇒sin()a Z πσξ+=当0ξ→时,sin,cos1222bbbπππξξξ==⇒sin()sincos cos sin22222a a a bbbbbπππππξξξ+=+σcossin222a a bbbπππξ=+2222[sin()]()cos 2cos sin(sin)2222222a a a a a bbbbbb bπππππππξξξ+=++22[sin()](sin )2cos sin22222a a a a bbbbbπππππξξ⇒+-=sinaZ ξπσ→⇒=sinlim aK ξπσ→⇒===Ⅰ=取w M =修正系数,大于1,表示其他裂纹存在对K Ⅰ的影响. 若裂纹间距离比裂纹本身尺寸大很多(2125a b ≤)可不考虑相互作用,按单个裂纹计算.二、无限大平板Ⅱ、Ⅲ型裂纹问题应力强度因子的计算 1.Ⅱ型裂纹应力强度因子的普遍表达形式(无限大板):lim (K Z ξξ→=Ⅱ2.无限大平板中的周期性的裂纹,且在无限远的边界上处于平板面内的纯剪切力作用.τsin()zZ z πτ=sin()()a Z πτξξ+=lim ()K ξξ→⇒==Ⅱ3.Ⅲ型裂纹应力强度因子的普遍表达形式(无限大板):lim ()K ξξ→=Ⅲ4.周期性裂纹:K =§2-2 深埋裂纹的应力强度因子的计算1950年，格林和斯内登分析了弹性物体的深埋的椭圆形裂纹邻域内的应力和应变，得到椭圆表面上任意点,沿y 方向的张开位移为:1222022(1)x z y y a c=--其中:202(1)ay E μσ-=Γ.Γ为第二类椭圆积分.有φϕ= (于仁东书) 1222220[sin ()cos ]a d cπϕϕϕ=+⎰(王铎书)1962年,Irwin 利用上述结果计算在这种情况下的应力强度因子σ原裂纹面11cos ,sin z x ρϕρϕ==又222222221111221x z c x a z a c a c+=⇒+= ⇒ρ=假设:椭圆形裂纹扩展时,其失径ρ的增值r 与ρ成正比.r f ρ= (f 远小于1)r f ρ⇒==边缘上任一点(,)p x z ''',有:1()sin (1)sin (1)x r f f x ρϕρϕ'=+=+=+1()cos (1)z r f z ρϕ'=+=+11(,),(,)p x z p x z '''⇒均在0y =的平面内. 222242222(1)c x a z f a c a c ''''''⇒+=+=⇒新的裂纹面仍为椭圆.长轴(1)c f c '=+,短轴(1)a f a '=+. ⇒y 向位移22002(1)2(1)(1)(1)a f a y f y E E μσμσϕϕ'--+'===+原有裂纹面:222220()1x z ya c y ++=扩展后裂纹面:222220()1x z y a c y '''++='''以1x x '=,1z z '=,代入⇒原有裂纹面的边缘y 向位移y ',有2222211112222222011(1)(1)x z x z y y a c f a f c'=-+=--'''++。

应力强度因子的数值计算方法一、引言数值计算方法通过将裂纹尖端的应力场分布模拟为一个虚拟的数学模型，利用计算机进行数值求解来得到应力强度因子的数值。

数值计算方法通常分为两种类型：直接方法和间接方法。

1.直接方法直接方法是指直接通过有限元分析软件求解裂纹尖端的应力场分布，并通过一些后处理技术来计算应力强度因子。

其中最常用的方法是J积分法和节点法。

（1）J积分法：J积分法是一种常用的裂纹应力强度因子计算方法，它通过在裂纹尖端附近引入一个虚拟断裂面，将裂纹尖端附近的应力场分布（由有限元分析得到）转化为裂纹尖端处的应力强度因子。

具体计算方法较为复杂，一般需要通过数值积分的方法求解。

（2）节点法：节点法是一种基于有限元网格节点的方法，其基本思想是通过增加节点对裂纹尖端附近的应力场进行离散，利用节点处的应力场计算应力强度因子。

节点法相对于J积分法计算简单，但适用条件较为有限。

2.间接方法间接方法是指通过已知应力场的变化率来计算应力强度因子的方法。

常用的间接方法有格里菲斯准则法、欠奇性法和EOS法。

（1）格里菲斯准则法：格里菲斯准则法是最早提出的计算裂纹扩展的方法之一，基于弹性力学理论和线弹性断裂力学基本假设，通过对裂纹尖端周围应力场的分析，得到应力强度因子与裂纹尖端形状和尺寸以及应力场的关系。

（2）欠奇性法：欠奇性法是一种基于能量原理的裂纹尖端应力强度因子计算方法，通过构造合适的应变能表达式和裂纹尖端应力强度因子的定义，利用应变能的分式展开求解裂纹尖端处的应力强度因子。

（3）EOS法：EOS法是一种在裂纹尖端周围选取合适的控制体，通过求解控制体内外表面的应力分布，建立应力强度因子与表面应力之间的关系，从而计算裂纹尖端处的应力强度因子。

三、应用场景1.断裂力学：数值计算方法可以用于预测和分析裂纹扩展行为，在断裂力学领域中有着重要的应用。

通过计算裂纹尖端的应力强度因子，可以评估材料的断裂韧性和脆性。

2.疲劳分析：3.材料破坏：数值计算方法可以用于分析材料的破坏机理和破坏行为。

ABAQUS计算裂纹尖端应力强度因子有效性的算例研究摘要：在实际工程领域中，相当部分的脆性材料总是不可避免的存在着裂纹或是缺陷。

在实际环境中材料的受力往往是相当复杂的。

基于ABAQUS平台的裂纹仿真软件，它具有简单易用的特点。

通过算例分析验证表明，该软件的计算结果具有较高的精度，完全可以用于实际工程问题的计算，通过分析验证表明该软件的设计是成功的。

此外，今后可以在它的基础上进行更多功能扩展，从而使它拥有分析更为复杂问题的能力。

关键词：裂纹；应力强度因子；断裂力学；ABAQUS引言材料在成型和加工过程中在其内部造成了很多缺陷，而其破坏正好均源于构件内部的微小裂纹，所以研究带裂纹的物体力学性能具有十分重要的意义。

图1存在于岩石和混凝土地面中的裂缝1920年， Griffith[1-2]提出了在材料中存在裂纹的设想，而从Irwin[]3-4]在1957年提出了应力强度因子以及其后形成的断裂韧度的概念后，断裂力学理论出现了重大的突破，奠定了线弹性断裂力学的基础。

1基本原理近年来以数值分析为基础的手段来解决断裂力学相关问题的技术得到了广泛的发展应用，并且不断的调整完善。

该技术在一定程度上较好的克服了实验条件下的不足。

对于线弹性断裂力学而言，裂尖区域的位移场、应力、应变场由应力强度因子决定，故而通过有限元计算的结果来得到具体的应力强度因子的值是线弹性断裂力学中用有限元法的基本要求。

1.1 ABAQUS求解裂纹尖端的应力强度因子传统的有限元在计算裂纹尖端的应力强度因子的时候，无可避免地遇到裂尖复杂应力场和位移场的计算，J积分则可以完全避免这种复杂的处理过程。

为了计算二维情况下的J积分，ABAQUS定义了围绕裂纹尖端由单元组成的环形的积分域，如下图所示。

图2 ABAQUS中围线的定义ABAQUS在计算围线积分时，采用的是先计算出围线上面所取的若干个离散点处J积分值，然后乘以每个点对应的加权值后，所有点相加来近似地求解出围线积分，即J积分的值和，进而得到复合裂纹的应力强度因子和。