使用ABAQUS计算应力强度因子

使用ABAQUS计算应力强度因子应力强度因子（Stress Intensity Factor，简称SIF）是应力场的一种特征参数，用于描述应力状态下混合模式断裂的倾向性。

它在断裂力学和疲劳断裂力学中起着非常重要的作用。

在ABAQUS软件中，可以通过线性弹性断裂力学方法来计算应力强度因子。

ABAQUS中计算SIF的方法通常分为两步：1.求解应力场2.计算SIF在求解应力场时，可以采用以下几种途径：1.固定边界条件：如果边界条件已知并且不会发生变化，则可以直接固定边界条件来求解应力场。

这种方法适用于简单的几何形状和加载情况。

2.施加约束：对于复杂几何形状和加载情况，可以施加约束来求解应力场。

例如，可以在加载边界上施加位移或力，并在其他边界上施加自由边界条件。

ABAQUS软件将通过求解线性弹性方程来获得应力场。

3.等效边界法：对于无法通过上述两种方法求解应力场的情况，可以采用等效边界法。

该方法将复杂几何体简化为等效的几何体，通过在等效边界上施加约束来求解应力场。

然后，可以使用所得的应力场计算SIF。

在计算SIF时，可以采用两种方法：1.J积分方法：这是一种基于应变能的方法，通过计算闭合路径上的应力和应变来计算SIF。

ABAQUS提供了J积分的计算方法，可以直接计算SIF。

2.基于位移法：这是一种基于位移的方法，通过计算表面位移场的奇异性来计算SIF。

ABAQUS也提供了这种方法的计算选项。

计算SIF的步骤一般如下：1.定义几何模型和输入材料参数。

2.设置边界条件和加载条件。

3.运行ABAQUS求解应力场。

4.运行相应的计算器（如J计算器或位移计算器）以计算SIF。

5.根据得到的SIF结果进行进一步的断裂力学分析。

需要注意的是，计算SIF是一个相对复杂的过程，需要对模型几何形状、边界条件、加载条件和材料参数等进行仔细考虑和设置。

此外，模型的网格划分和数值求解的精度也会对计算结果产生影响，因此需要进行适当的验证和后处理分析。

如何使用ABAQUS计算应力强度因子ABAQUS是一种广泛使用的有限元分析软件，可用于计算应力强度因子。

应力强度因子用于评估材料中的裂纹扩展性能，是断裂力学中的重要参数。

以下是使用ABAQUS计算应力强度因子的一般步骤：1.准备模型：在使用ABAQUS计算应力强度因子之前，需要先准备好模型。

模型应包含有裂纹的几何形状，以及材料的属性。

2.确定边界条件：要使用ABAQUS计算应力强度因子，必须指定适当的边界条件。

这些条件可以是约束的位移或力。

3.定义材料特性：为了计算应力强度因子，需要定义材料的特性，如弹性模量和泊松比。

这些特性通常可以从实验数据中获取。

4.创建网格：在使用ABAQUS计算应力强度因子之前，需要对模型进行离散化处理，将其划分为有限个单元。

这可以通过使用ABAQUS提供的网格生成工具来完成。

5.应用载荷：定义适当的载荷类型和大小，以便在模型上施加负载。

这可以是施加在边界上的力或位移。

6.定义裂纹：使用ABAQUS的初始裂纹命令或裂纹离散化工具来创建裂纹几何。

裂纹可以是直线裂纹，也可以是不规则或曲线裂纹。

7.定义断裂准则：使用ABAQUS的断裂准则定义工具，指定在何种条件下认为破坏发生。

常用的断裂准则包括应力强度因子法和能量释放率法。

8.运行ABAQUS求解器：在定义了模型、边界条件、材料特性、网格和载荷之后，可以运行ABAQUS求解器。

根据模型的复杂程度，可能需要较长的计算时间。

9.后处理结果：一旦ABAQUS求解器完成计算，可以使用ABAQUS提供的后处理工具来分析结果。

这些工具可以用于计算应力强度因子及其分布。

10.计算应力强度因子：通过使用ABAQUS的应力强度因子计算工具，可以计算裂纹尖端处的应力强度因子。

这些结果可以用来预测裂纹的扩展和破坏行为。

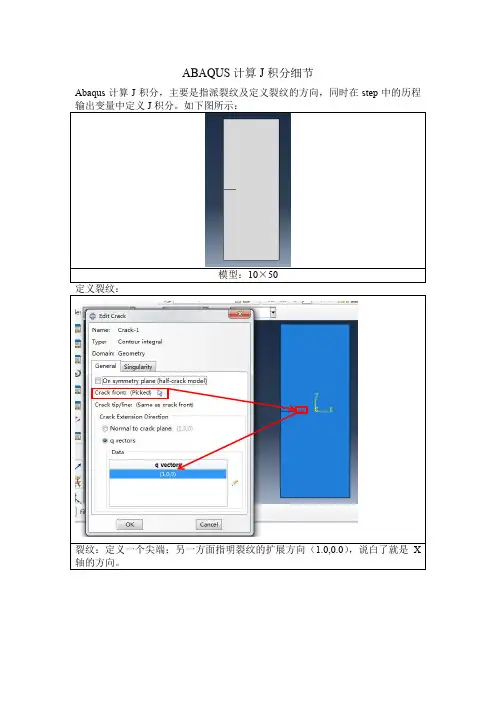
ABAQUS计算J积分细节Abaqus计算J积分，主要是指派裂纹及定义裂纹的方向，同时在step中的历程模型：10×50裂纹：定义一个尖端；另一方面指明裂纹的扩展方向（1.0,0.0），说白了就是X积分数值,图中输入10，则输出10个J积分值计算包含裂纹尖端的包络区域的面积即为J积分避开裂纹尖端塑形区域的不可计算的特性。

同时J积分的计算数值与积分路径无从以上图例可以看出J积分数值区域稳定。

疑问：为何计算多个积分点，是否最后的稳定数值就是需要计算的J积分数值？J积分应该是数值，而不是多个不同的数值。

我个人觉得最后的稳定数值应该是需要计算的积分数值。

从dat文件到inp文件，找到积分区域。

pickseted12以及pickseted13都是节点4，坐标如图所示，在cad模型中的位置如箭头指向，即裂纹尖端。

详细的需要看一下abaqus帮助文档，关于J积分的计算细节。

积分点的个数的意义我还没有搞清楚。

对于应力强度因子K，表征裂纹尖端受力的一个参量，在裂纹尖端的应力场的一定范围内，不同的节点计算数值大体是相同的。

计算应力强度因子：可以利用abaqus直接输出，也可以利用公式计算应力强度因子，以下为利用有限元法计算应力强度因子：计算应力强度因子：从上图可以看出，计算应力强度应力的点与计算J积分的点是一致的。

Abaqus计算的应力强度因子为裂尖处的应力强度因子。

下面我们利用有限元法计算y=0处的应力强度因子，最后外推到裂尖处的应力强度因子。

选取不同的半Abaqus计算J积分注意事项：(1)一、Interaction模块1.1 预制裂纹（步骤：菜单/special/crack/assign seam）注意：并不是作裂纹分析都要定义seam，如果你的裂纹不是一条缝，而是一个缺口，则不需要assign seam，直接走下一步（定义裂纹）就行。

1.2 创建裂纹（步骤：菜单/special/crack/create，type：contour integral）—crack front：crack front是用来定义第一围线积分的区域，2D下我们可以选择包围裂尖点的面，3D则选择包围裂尖线的面；另外还有一种定义crack front的方法，就是直接选择裂尖点（2D）或裂尖线3D），用这个方法定义crack front不需要再定义下一步的crack tip/line，比较简便，两种方法算出的结果没有明显的差别，其实只是影响积分路线的问题，但是J积分值是路径无关的，看个人喜好吧—crack tip/line：这个比较好理解就是裂尖点（2D）或线（3D），如果我们在上一步中用方法二定义crack front，这一步就直接跳过了—crack extension direction（定义裂纹扩展方向）：这里定义的其实是一个虚拟的裂纹扩展方向，定义了这个参考方向后，我们才能通过输出的角度判断裂纹扩展方向，可以通过两种方法：（1）q vector：输入一个方向，用来作为计算裂纹的扩展方向的参考方向；（2）normal to crack plane：crack plane表示裂纹的对称面（当裂纹在一个平面内时，可能需要分开定义多个裂纹），这种方法下我们只需定义裂纹面的法线方向，通过（t表示裂纹尖端的切线）, 会在每个节点得出一个q方向；（3）注意：q的方向对输出的应力强度因子，J积分等都会有影响，一般情况下，q最好在裂纹平面内，且垂直于裂尖线的切线，否则算出的应力强度因子，J积分值等等在不同围线积分中会差别较大。

------------------------------------------------------------------------------------------------------- 如何使用ABAQUS计算应力强度因子Simwefanhj（fanhjhj@）2011.9.9------------------------------------------------------------------------------------------------------- 问题描述：以无限大平板含有一贯穿裂纹为例，裂纹长度为10mm（2a），在远场受双向均布拉应力σ＝100N/mm2。

按解析解，此I型裂纹计算出的应力＝396.23（N.mm-3/2）强度因子πσaK=I以下为使用ABAQUS6.10的计算该问题的过程。

第一步：进入part模块①建立平板part（2D Planar;Deformation;shell），平板的尺寸相对于裂纹足够大，本例的尺寸为100×50（mm）。

②使用Partation Face:sketch工具，将part分隔成如图1形式。

图1第二步：进入property模块①建立弹性材料；②截面选择平面问题的solid，homogeneous；③赋予截面。

第三步：进入Assembly模块不详述。

需注意的是：实体的类型（instance type）选择independent。

第四步：进入mesh模块除小圈内使用CPS6单元外，其它位置使用CPS8单元离散（图2）。

裂纹尖端的奇异在interaction模块中（图4）考虑。

图2第五步：进入interaction模块①指定裂纹special/creak/assign seam，选中示意图3中的黄色线，done！②生成裂纹crack 1，special/crack/create,name：crack 1，type: contour integral.当提示选择裂纹前端时，选则示意图的红圈区域，当提示裂纹尖端区域时选择红圈的圆心，用向量q表示裂纹扩展方向（示意图3绿色箭头）。

Abaqus节点应力和单元应力分析在工程和科学领域中，节点应力和单元应力分析是非常重要的任务，它们可以帮助我们了解材料的行为和结构的稳定性。

Abaqus是一种常用的有限元分析软件，可以用于进行节点应力和单元应力分析。

节点应力分析节点应力是指在有限元模型中每个节点处的应力值。

通过节点应力分析，我们可以确定结构中各个位置的最大、最小以及平均应力值，并且可以对结构进行强度评估。

Abaqus使用有限元方法来计算节点应力。

有限元方法将结构离散化为许多小型单元，然后通过求解线性方程组来估计每个节点处的位移和变形。

根据位移和变形信息，可以计算出每个节点处的应力。

要进行节点应力分析，在Abaqus中需要完成以下步骤：1.创建几何模型：使用Abaqus提供的几何建模工具来创建你想要分析的结构模型。

2.定义材料属性：根据所选材料的特性，在Abaqus中定义材料属性。

这些属性包括弹性模量、泊松比等。

3.设置边界条件：定义结构上的边界条件，例如固定支撑、施加的力或位移等。

4.网格划分：将结构离散化为小型单元，并生成网格。

可以根据需要调整网格密度。

5.定义分析步骤：通过定义加载步骤和分析类型来设置节点应力分析。

6.运行分析：在Abaqus中运行节点应力分析，并获得每个节点处的应力结果。

单元应力分析单元应力是指在有限元模型中每个单元内部的应力值。

通过单元应力分析，我们可以了解结构中不同单元的受力情况，从而评估结构的稳定性和强度。

Abaqus使用有限元方法计算单元应力。

在有限元模型中，结构被划分为许多小型单元，每个单元都有自己的材料属性和几何特性。

通过求解线性方程组，可以得到每个单元内部的位移和变形信息，并根据这些信息计算出每个单元内部的应力。

要进行单元应力分析，在Abaqus中需要完成以下步骤：1.创建几何模型：使用Abaqus提供的几何建模工具来创建你想要分析的结构模型。

2.定义材料属性：根据所选材料的特性，在Abaqus中定义材料属性。

基于ABAQUS的裂纹形状对应力强度因子的影响作者：李宗揆来源：《中国科技博览》2015年第12期[摘要]工程实际应用中的构件几乎全部是带裂缝工作，介绍了ABAQUS软件断裂力学计算模块，采用ABAQUS分析软件对三点弯曲试验进行裂纹分析，讨论在不同开裂方向对于裂纹尖端应力强度因子的影响，并得出相关结论。

[关键词]J积分；应力强度因子；ABAQUS中图分类号：O346.11 文献标识码：A 文章编号：1009-914X（2015）12-0100-011 前言实际工程中构件通常都是带裂缝工作，此时传统的屈服判据失效，不能再去判断结构发生断裂的时机，为此，我们应当借助断裂力学得到新的断裂判据。

断裂的发生源于裂纹的扩展，而裂纹的失稳扩展通常由裂纹端点开始。

裂纹端点区应力应变场强度的大小是裂纹能否扩展的决定因素，因此需要找到一个能够表征裂纹端点区应力应变场强度的参量。

断裂力学中使用应力强度因子的概念去衡量裂纹尖端的应力场强度，当裂纹尖端区应力场的形式恒定，其强度完全由应力强度因子的大小来确定。

本文通过有限元分析，讨论三点弯曲试验中，处于同样荷载状况下，不同的开裂角度对于梁体裂纹尖端区应力强度因子的影响，以期得到一个合理的变化规律。

2 计算分析2.1 断裂力学的能量方法及应力强度因子在断裂的过程中，裂纹尖端处要释放出一定的能量。

因此，必须结合能量释放率寻求裂纹尖端附近应力—应变场的解答。

在二维Ⅰ型裂纹问题中，考虑一个离裂纹端很近、位置在极坐标（r，θ）的平面问题的应力单元，由Westergaard应力函数法给出裂纹尖端区域应力场的解析解为当r→0时，应力分量都会趋于无穷大。

裂纹问题的关键是计算裂纹尖端处的应力场，为保证计算精度，裂纹尖端单元应设计为奇异性单元，并在此周围区域局部加密。

是由裂纹下表面某点逆时针绕行到裂纹上表面某点的简单的积分围道，表示收缩到裂纹尖端；q是虚拟裂纹扩展方向的单位向量；n是的外法线方向；H的定义为，其中弹性材料W是弹性应力能量。

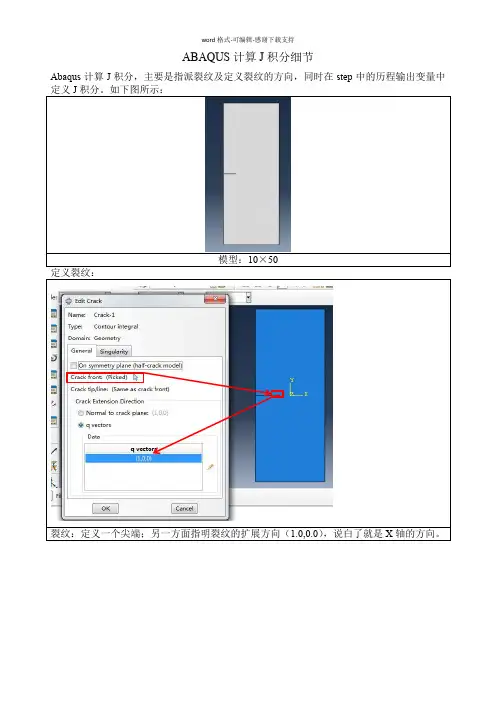
ABAQUS计算J积分细节Abaqus计算J积分，主要是指派裂纹及定义裂纹的方向，同时在step中的历程输出变量中定义J积分。

如下图所示：模型：10×50定义裂纹：裂纹：定义一个尖端；另一方面指明裂纹的扩展方向（1.0,0.0），说白了就是X轴的方向。

Step中输出裂纹参量：积分数值,图中输入10，则输出10个J积分值J积分的理解：计算包含裂纹尖端的包络区域的面积即为J积分尖端塑形区域的不可计算的特性。

同时J积分的计算数值与积分路径无关。

以下为六个计算从以上图例可以看出J积分数值区域稳定。

疑问：为何计算多个积分点，是否最后的稳定数值就是需要计算的J积分数值？J积分应该是数值，而不是多个不同的数值。

我个人觉得最后的稳定数值应该是需要计算的积分数值。

从dat文件到inp文件，找到积分区域。

pickseted12以及pickseted13都是节点4，坐标如图所示，在cad模型中的位置如箭头指向，即裂纹尖端。

详细的需要看一下abaqus帮助文档，关于J积分的计算细节。

积分点的个数的意义我还没有搞清楚。

对于应力强度因子K，表征裂纹尖端受力的一个参量，在裂纹尖端的应力场的一定范围内，不同的节点计算数值大体是相同的。

计算应力强度因子：可以利用abaqus直接输出，也可以利用公式计算应力强度因子，以下为利用有限元法计算应力强度因子：计算应力强度因子：从上图可以看出，计算应力强度应力的点与计算J积分的点是一致的。

Abaqus计算的应力强度因子为裂尖处的应力强度因子。

下面我们利用有限元法计算y=0处的应力强度因子，最后外推到裂尖处的应力强度因子。

选取不同的半径r值计算得到的应力Abaqus计算J积分注意事项：(1)一、Interaction模块(2) 1.1 预制裂纹（步骤：菜单/special/crack/assign seam）(3)注意：并不是作裂纹分析都要定义seam，如果你的裂纹不是一条缝，而是一个缺口，则不需要assign seam，直接走下一步（定义裂纹）就行。

ABAQUS中应力、应变详解
真实应力、名义应力、真实应变、名义应变的关系
名义应变，又称相对应变或工程应变、适用于小应变分析。

名义应变又可分线应变和切应变。

真实应变，又称对数应变；假设物体内两质点相距为L0, 经变形后距离为 Ln, 则相对线应变为
ε = （Ln-L0）/L0 ,这种相对线应变一般用于小应变情况。

而在实际变形过程中，长度L0系经过无穷多个中间的数值变成L, 如L0,L1,L2,L3 …… Ln-1,Ln, 其中相邻两长度相差均极微小，由 L0-Ln 的总的变形程度，可以近似地看作是各个阶段相对应变之和，
大多数实验数据常常是用名义应力和名义应变值给出的,所以我们应将其转换为真实应力和真实应变。

其转换公式如下：
塑性分析中的注意问题：对于大应变，真实应变和名义应变之间的差值就会很大，所以在给abaqus提供应力－应变数据时，一定要注意正确的给予赋值，在小应变的情况下，真实应变和名义应变之间的差别很小，不是很重要。

几何非线性开关打开时，ABAQUS中可输出LE（真实应变）、EE （弹性应变）、NE（名义应变）等
几何非线性开关关闭时，ABAQUS中可输出E（真实应变）、EE （弹性应变）等。

A B A Q U S 反复加载卸载应力应变计算说明1、 塑性模型采用Armstrong and Frederick model (AF 模型)[1] （1） 屈服准则（Mises 屈服）屈服函数为2)~~(:)~~(23Y s s F ---=αα 式中：s ~为应力偏量，α~为总背应力，Y 为屈服极限 （2） 流动准则（the associated flow rule ）式中：pε~为塑性应变对时间的微分，λ 为待定量[2]，σ~为应力张量 （3） 硬化准则<1> p h i i p i i )()()()(~~32~αζεα-= 式中：)(~i α为背应力分量对时间的微分；)(i h ，)(i ζ为材料常数为已知量，p为等效塑性应变对时间的微分。

<2> )1()(1)(0pMi i i e r Y Y ζ-=-+=∑式中：Y 为对应于等效塑性应变p 的屈服极限，0Y 为初始屈服极限为已知量，)(i r 为材料常数为已知量。

2、 反复加载卸载应力应变计算过程说明假设在受载前，物体的初始应力、应变以及背应力均为零 2.1加载过程计算<1> 外力不足以使得物体中的任何一点的Mises 应力值大于屈服极限此时：塑性应变、背应力均保持为零，屈服极限保持不变。

应力由e e D εσ~:~~~=计算，总应变值等于弹性应变。

<2> 外力使得物体中的任何一点的Mises 应力值大于屈服极限为了说明ABAQUS 是如何确定应变增量1~+∆n ε，有必要对ABAQUS 求解材料非线性问题进行简单介绍[3]。

ABAQUS 首先将载荷分为若干个微小增量，如图1所示。

当结构收到一个微小增量P ∆时，ABAQUS 用与初始结构位移相对应的初始刚度矩阵0K 和载荷增量P ∆计算出结构在这一增量后的位移修正a c 、修正后的位移值a u 和相应的新的刚度矩阵a K 。

ABAQUS 用新的刚度矩阵计算结构的内力a I ，载荷P 和a I 的差值为迭代的残余力a R 。

在ABAQUS 中对应力的部分理解1、三维空间中任一点应力有6个分量yz xz xy z y ,,,σσσσσσ，，x ，在ABAQUS 中分别对应S11，S22，S33，S12，S13，S23。

2、一般情况下，通过该点的任意截面上有正应力及其剪应力作用。

但有一些特殊截面，在这些截面上仅有正应力作用，而无剪应力作用。

称这些无剪应力作用的面为主截面，其上的正应力为主应力，主截面的法线叫主轴，主截面为互相正交。

主应力分别以321,,σσσ表示，按代数值排列（有正负号）为321σσσ≥≥。

其中321,,σσσ在ABAQUS 中分别对应Max. Principal 、Mid. Principal 、Min. Principal ，这三个量在任何坐标系统下都是不变量。

可利用最大主应力判断一些情况：比如混凝土的开裂，若最大主应力（拉应力）大于混凝土的抗拉强度，则认为混凝土开裂，同时通过显示最大主应力的法线方向，可以大致表示出裂缝的开裂方向等。

利用最小主应力，可以查看实体中残余压应力的大小等。

3、弹塑性材料的屈服准则3.1、Mises 屈服准则22132322212)()()(Sσσσσσσσ=-+-+- 其中s σ为材料的初始屈服应力。

在三维空间中屈服面为椭圆柱面；在二维空间中屈服面为椭圆。

Mises 等效应力的定义为：(牵扯到张量知识)其中 S 为偏应力张量，其表达式为其中为应力，I 为单位矩阵，p 为等效压应力（定义如下）：, 也就是我们常见的)(31z y x p σσσ++=。

还可以具体表达为：其中,,为偏应力张量（反应塑性变形形状的变化）。

q 在ABAQUS 中对应 Mises ，它有6个分量（随坐标定义的不同而变化）S11，S22，S33，S12，S13，S233.2、Trasca 屈服准则 主应力间的最大差值=2k若明确了321σσσ≥≥，则有k =-)(2131σσ，若不明确就需要分别两两求差值，看哪个最大。

Abaqus壳单元的应力结果
壳单元应力和应变分量的含义不同于实体单元。

默认情况下，实体单元的应力和应变分量都是基于全局坐标系，而壳单元的应力和应变分量是基于壳本身的局部坐标系。

如果在定义截面属性时指定了壳单元的局部坐标系，则应力、应变和截面力分量的方向都是基于此局部坐标系。

如果没有指定单元的局部坐标系，则采用默认的局部坐标系方向，其确定方法如下：（1）将全局坐标系的x方向在壳单元面上的投影作为局部坐标系的1方向（如下图左）。

如果全局坐标系的x方向与壳单元面法线方向的夹角≤0.1°，则将全局坐标系的z方向在壳单元面上的投影作为局部坐标第的1方向（如下图右）。

（2）局部坐标系的2方向与1方向夹角为90°，由右手螺旋法则确定，伸开右手，让四指的方向与壳单元节点编号顺序相同，大拇指的指向即为局部坐标系的3方向，局部坐标第的2方向也同时被确定。

对于包含位移自由度的壳单元，各个应力分量的含义如下：
S11：局部坐标系下1方向的正应力；
S22：局部坐标系下2方向的正应力；
S33：局部坐标系下3方向的正应力；
S12：局部坐标系下1、2方向的剪应力。

在局部坐标系下2、3方向和1、3方向没有剪应力分量存在，因此在Visualization功能模块中，场变量的输出结果中只胡S11、S22、S33、S12共4个分量。

_____________________。

基于ABAQUS的复杂裂纹应力强度因子的研究摘要：在实际工程领域，裂纹问题一直都是一个影响结构安全性的难题。

本文从现实工程角度出发，针对复杂裂纹的断裂破坏机理，采用基于ABAQUS的数值模拟技术，进行了深入的研究。

为了证明采用数值模拟技术研究复杂裂纹的可靠性，本文首先利用ABAQUS对其他学者做出的理论值进行了验证，结果表明理论和数值具有高度的吻合性。

然后进行了复杂裂纹在不同情况下的裂尖应力强度因子进行了研究。

从而为现实工程建设中一些不便于实验研究的复杂情况，提出了研究的可行性方法，具有较强的实践意义。

关键词：裂纹；应力强度因子；ABAQUS；数值模拟0 引言断裂力学是研究带裂纹体的强度和裂纹扩展规律的一门学科。

断裂力学的最早理论可以追溯到1920年，为了研究玻璃、陶瓷等脆性材料的实际强度比理论强度低的原因，Griffith[1-2]提出了在材料中存在裂纹的设想，而Irwin[3-4]在1957年提出了应力强度因子以及其后形成的断裂韧度的概念后，断裂力学理论出现了重大的突破，奠定了线弹性断裂力学的基础。

当前国内外许多学者[5-8]已将多裂纹问题作为主攻方向，但是受到诸多条件的制约，目前并未取得明显的成果。

1复杂裂纹研究的现实依据图（a）是位于四川的几大主要断裂带的分布图，在宏观上形成了V型的断层结构。

汶川Ms8.0级地震，就是龙门山断裂带在构造应力场长期作用下，积累的应变能突然释放的结果。

图（b）是2002年11月3日，阿拉斯加中部迪纳利断层发生了一次M w7.9级地震。

从图（b）可以看出三条主断裂层形成了典型的的分支结构，究断层的性质对于预知、了解地质作用，估计可能发生的破坏具有重要参考价值。

图1 现实V型、Y型裂纹存在模型2 Y型裂纹的应力强度因子研究2.1有限元建模中间带有裂纹的双轴压缩试件，如图2所示，在相关断裂力学的试验分析中被广泛应用。

故此，本文以此典型试件作为研究对象，进行数值模拟计算。

abaqus中le计算方法abaqus中的le计算方法引言：在工程设计和科学研究中，常常需要对材料的力学性能进行分析和评估。

有限元分析方法是一种常用的工具，可以通过数值模拟的方式来计算结构的应力和变形等力学参数。

而abaqus软件则是一款常用的有限元分析软件，具有强大的计算能力和广泛的应用范围。

其中，le计算方法是abaqus中一种重要的分析方法，本文将对其原理和应用进行详细介绍。

一、le计算方法的原理le计算方法是abaqus中一种基于拉伸试验数据进行弹性模量和屈服强度计算的方法。

其原理主要包括以下几个步骤：1. 数据输入：首先需要准备拉伸试验数据，包括应力-应变曲线和应变的计算方法。

这些数据可以通过实验测量获得，也可以通过材料的力学性能参数进行估计。

2. 材料模型的选择：根据实际情况，选择合适的材料模型来描述材料的力学性能。

常用的材料模型包括线性弹性模型和非线性弹性模型等。

3. 弹性模量的计算：根据拉伸试验数据和选定的材料模型，可以通过拟合方法计算材料的弹性模量。

拟合方法可以是最小二乘法或其他数学方法。

4. 屈服强度的计算：根据拉伸试验数据和选定的材料模型，可以通过拟合方法计算材料的屈服强度。

拟合方法可以是最小二乘法或其他数学方法。

5. 结果输出：最后，将计算得到的弹性模量和屈服强度输出到abaqus软件中，用于后续的有限元分析。

二、le计算方法的应用le计算方法在工程设计和科学研究中具有广泛的应用。

以下是一些常见的应用场景：1. 材料评估：通过le计算方法可以对不同材料的力学性能进行评估。

例如，可以比较不同材料的弹性模量和屈服强度，选择合适的材料用于特定的工程应用。

2. 结构分析：le计算方法可以用于预测结构在不同载荷情况下的应力和变形。

通过将计算得到的弹性模量和屈服强度输入到abaqus 软件中，可以进行更加准确的有限元分析。

3. 材料改进：通过le计算方法可以评估不同处理方式对材料力学性能的影响。