abaqus计算应力强度因子

------------------------------------------------------------------------------------------------------- 如何使用ABAQUS计算应力强度因子Simwefanhj（fanhjhj@）2011.9.9------------------------------------------------------------------------------------------------------- 问题描述：以无限大平板含有一贯穿裂纹为例，裂纹长度为10mm（2a），在远场受双向均布拉应力σ＝100N/mm2。

按解析解，此I型裂纹计算出的应力＝396.23（N.mm-3/2）强度因子πσaK=I以下为使用ABAQUS6.10的计算该问题的过程。

第一步：进入part模块①建立平板part（2D Planar;Deformation;shell），平板的尺寸相对于裂纹足够大，本例的尺寸为100×50（mm）。

②使用Partation Face:sketch工具，将part分隔成如图1形式。

图1第二步：进入property模块①建立弹性材料；②截面选择平面问题的solid，homogeneous；③赋予截面。

第三步：进入Assembly模块不详述。

需注意的是：实体的类型（instance type）选择independent。

第四步：进入mesh模块除小圈内使用CPS6单元外，其它位置使用CPS8单元离散（图2）。

裂纹尖端的奇异在interaction模块中（图4）考虑。

图2第五步：进入interaction模块①指定裂纹special/creak/assign seam，选中示意图3中的黄色线，done！②生成裂纹crack 1，special/crack/create,name：crack 1，type: contour integral.当提示选择裂纹前端时，选则示意图的红圈区域，当提示裂纹尖端区域时选择红圈的圆心，用向量q表示裂纹扩展方向（示意图3绿色箭头）。

使用ABAQUS计算应力强度因子应力强度因子（Stress Intensity Factor，简称SIF）是应力场的一种特征参数，用于描述应力状态下混合模式断裂的倾向性。

它在断裂力学和疲劳断裂力学中起着非常重要的作用。

在ABAQUS软件中，可以通过线性弹性断裂力学方法来计算应力强度因子。

ABAQUS中计算SIF的方法通常分为两步：1.求解应力场2.计算SIF在求解应力场时，可以采用以下几种途径：1.固定边界条件：如果边界条件已知并且不会发生变化，则可以直接固定边界条件来求解应力场。

这种方法适用于简单的几何形状和加载情况。

2.施加约束：对于复杂几何形状和加载情况，可以施加约束来求解应力场。

例如，可以在加载边界上施加位移或力，并在其他边界上施加自由边界条件。

ABAQUS软件将通过求解线性弹性方程来获得应力场。

3.等效边界法：对于无法通过上述两种方法求解应力场的情况，可以采用等效边界法。

该方法将复杂几何体简化为等效的几何体，通过在等效边界上施加约束来求解应力场。

然后，可以使用所得的应力场计算SIF。

在计算SIF时，可以采用两种方法：1.J积分方法：这是一种基于应变能的方法，通过计算闭合路径上的应力和应变来计算SIF。

ABAQUS提供了J积分的计算方法，可以直接计算SIF。

2.基于位移法：这是一种基于位移的方法，通过计算表面位移场的奇异性来计算SIF。

ABAQUS也提供了这种方法的计算选项。

计算SIF的步骤一般如下：1.定义几何模型和输入材料参数。

2.设置边界条件和加载条件。

3.运行ABAQUS求解应力场。

4.运行相应的计算器（如J计算器或位移计算器）以计算SIF。

5.根据得到的SIF结果进行进一步的断裂力学分析。

需要注意的是，计算SIF是一个相对复杂的过程，需要对模型几何形状、边界条件、加载条件和材料参数等进行仔细考虑和设置。

此外，模型的网格划分和数值求解的精度也会对计算结果产生影响，因此需要进行适当的验证和后处理分析。

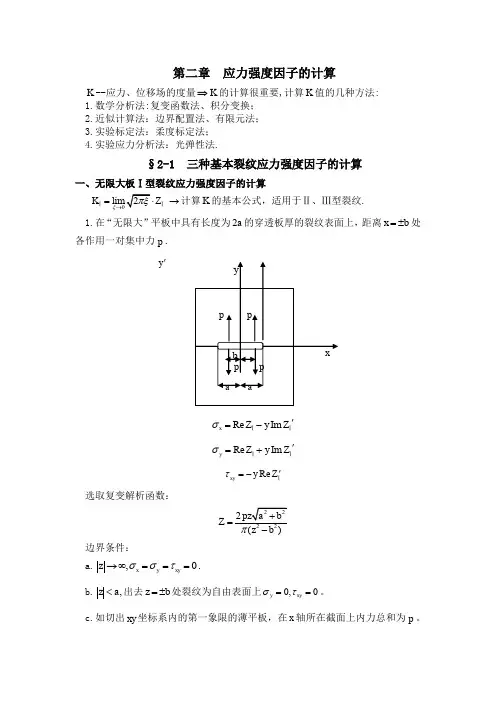
第二章 应力强度因子的计算K --应力、位移场的度量⇒K 的计算很重要,计算K 值的几种方法: 1.数学分析法:复变函数法、积分变换； 2.近似计算法：边界配置法、有限元法； 3.实验标定法：柔度标定法； 4.实验应力分析法：光弹性法.§2-1 三种基本裂纹应力强度因子的计算一、无限大板Ⅰ型裂纹应力强度因子的计算K Z ξ→=→ⅠⅠ计算K 的基本公式，适用于Ⅱ、Ⅲ型裂纹.1.在“无限大”平板中具有长度为2a 的穿透板厚的裂纹表面上，距离x b =±处各作用一对集中力p .Re Im x Z y Z σ'=-ⅠⅠRe Im y Z y Z σ'=+ⅠⅠRe xy y Z τ'=-Ⅰ选取复变解析函数：222()Z z b π=- 边界条件：a.,0x y xy z σστ→∞===.b.,z a <出去z b =±处裂纹为自由表面上0,0y xy στ==。

c.如切出xy 坐标系内的第一象限的薄平板，在x 轴所在截面上内力总和为p 。

y '以新坐标表示：Z=⇒lim()K Zξξ→==Ⅰ2.在无限大平板中,具有长度为2a的穿透板厚的裂纹表面上，在距离1x a=±的范围内受均布载荷q作用.利用叠加原理:微段→集中力qdx→dK=Ⅰ⇒K=⎰Ⅰ令cos cosx a aθθ==,cosdx a dθθ=⇒111sin()1cos22(cosaa aaaK daθθθ--==Ⅰ当整个表面受均布载荷时,1a a→.⇒12()aaK-==Ⅰ3.受二向均布拉力作用的无限大平板,在x轴上有一系列长度为2a,间距为2b 的裂纹.边界条件是周期的: a. ,y x z σσσ→∞==.b.在所有裂纹内部应力为零.0,,22y a x a a b x a b =-<<-±<<±在区间内0,0y x y στ==c.所有裂纹前端y σσ> 单个裂纹时Z =又Z 应为2b 的周期函数⇒sinzZ πσ=采用新坐标:z a ξ=-⇒sin()a Z πσξ+=当0ξ→时,sin,cos1222bbbπππξξξ==⇒sin()sincos cos sin22222a a a bbbbbπππππξξξ+=+σcossin222a a bbbπππξ=+2222[sin()]()cos 2cos sin(sin)2222222a a a a a bbbbbb bπππππππξξξ+=++22[sin()](sin )2cos sin22222a a a a bbbbbπππππξξ⇒+-=sinaZ ξπσ→⇒=sinlim aK ξπσ→⇒===Ⅰ=取w M =修正系数,大于1,表示其他裂纹存在对K Ⅰ的影响. 若裂纹间距离比裂纹本身尺寸大很多(2125a b ≤)可不考虑相互作用,按单个裂纹计算.二、无限大平板Ⅱ、Ⅲ型裂纹问题应力强度因子的计算 1.Ⅱ型裂纹应力强度因子的普遍表达形式(无限大板):lim (K Z ξξ→=Ⅱ2.无限大平板中的周期性的裂纹,且在无限远的边界上处于平板面内的纯剪切力作用.τsin()zZ z πτ=sin()()a Z πτξξ+=lim ()K ξξ→⇒==Ⅱ3.Ⅲ型裂纹应力强度因子的普遍表达形式(无限大板):lim ()K ξξ→=Ⅲ4.周期性裂纹:K =§2-2 深埋裂纹的应力强度因子的计算1950年，格林和斯内登分析了弹性物体的深埋的椭圆形裂纹邻域内的应力和应变，得到椭圆表面上任意点,沿y 方向的张开位移为:1222022(1)x z y y a c=--其中:202(1)ay E μσ-=Γ.Γ为第二类椭圆积分.有φϕ= (于仁东书) 1222220[sin ()cos ]a d cπϕϕϕ=+⎰(王铎书)1962年,Irwin 利用上述结果计算在这种情况下的应力强度因子σ原裂纹面11cos ,sin z x ρϕρϕ==又222222221111221x z c x a z a c a c+=⇒+= ⇒ρ=假设:椭圆形裂纹扩展时,其失径ρ的增值r 与ρ成正比.r f ρ= (f 远小于1)r f ρ⇒==边缘上任一点(,)p x z ''',有:1()sin (1)sin (1)x r f f x ρϕρϕ'=+=+=+1()cos (1)z r f z ρϕ'=+=+11(,),(,)p x z p x z '''⇒均在0y =的平面内. 222242222(1)c x a z f a c a c ''''''⇒+=+=⇒新的裂纹面仍为椭圆.长轴(1)c f c '=+,短轴(1)a f a '=+. ⇒y 向位移22002(1)2(1)(1)(1)a f a y f y E E μσμσϕϕ'--+'===+原有裂纹面:222220()1x z ya c y ++=扩展后裂纹面:222220()1x z y a c y '''++='''以1x x '=,1z z '=,代入⇒原有裂纹面的边缘y 向位移y ',有2222211112222222011(1)(1)x z x z y y a c f a f c'=-+=--'''++2222221111112222221(12)(12)12()x z x z x z f f f a c a c a c----=--++2f =2222200022(1)2y fy f f y fy ''⇒==+又f =⇒2y '=设各边缘的法向平面为平面应变,有:31)sin sin ]22v k θθ=+- 其中34k μ=-当θπ=时24(1)v K E μ-=222216(1)2I r K E μπ-⇒=22021E ()41I K y acπμ⇒=-又202(1)ay E μσϕ-=14122222()(sin cos )I a K c a cϕϕφ⇒=+在椭圆的短轴方向上，即2πϕ=，有I ImaxK K φ== 危险部位 →椭圆片状深埋裂纹的应力强度因子当a c =时→圆片状裂纹，2πφ=2I K π⇒=§2-3 半椭圆表面裂纹的应力强度因子计算一、表面浅裂纹的应力强度因子当a B （板厚）→线裂纹⇒可以忽略后自由表面对A 点应力强度的影响 欧文假设：半椭圆片状表面线裂纹I K 与深埋椭圆裂纹的I K 之比等于边裂纹平板与中心裂纹平板的I K 值之比。

如何使用ABAQUS计算应力强度因子ABAQUS是一种广泛使用的有限元分析软件，可用于计算应力强度因子。

应力强度因子用于评估材料中的裂纹扩展性能，是断裂力学中的重要参数。

以下是使用ABAQUS计算应力强度因子的一般步骤：1.准备模型：在使用ABAQUS计算应力强度因子之前，需要先准备好模型。

模型应包含有裂纹的几何形状，以及材料的属性。

2.确定边界条件：要使用ABAQUS计算应力强度因子，必须指定适当的边界条件。

这些条件可以是约束的位移或力。

3.定义材料特性：为了计算应力强度因子，需要定义材料的特性，如弹性模量和泊松比。

这些特性通常可以从实验数据中获取。

4.创建网格：在使用ABAQUS计算应力强度因子之前，需要对模型进行离散化处理，将其划分为有限个单元。

这可以通过使用ABAQUS提供的网格生成工具来完成。

5.应用载荷：定义适当的载荷类型和大小，以便在模型上施加负载。

这可以是施加在边界上的力或位移。

6.定义裂纹：使用ABAQUS的初始裂纹命令或裂纹离散化工具来创建裂纹几何。

裂纹可以是直线裂纹，也可以是不规则或曲线裂纹。

7.定义断裂准则：使用ABAQUS的断裂准则定义工具，指定在何种条件下认为破坏发生。

常用的断裂准则包括应力强度因子法和能量释放率法。

8.运行ABAQUS求解器：在定义了模型、边界条件、材料特性、网格和载荷之后，可以运行ABAQUS求解器。

根据模型的复杂程度，可能需要较长的计算时间。

9.后处理结果：一旦ABAQUS求解器完成计算，可以使用ABAQUS提供的后处理工具来分析结果。

这些工具可以用于计算应力强度因子及其分布。

10.计算应力强度因子：通过使用ABAQUS的应力强度因子计算工具，可以计算裂纹尖端处的应力强度因子。

这些结果可以用来预测裂纹的扩展和破坏行为。

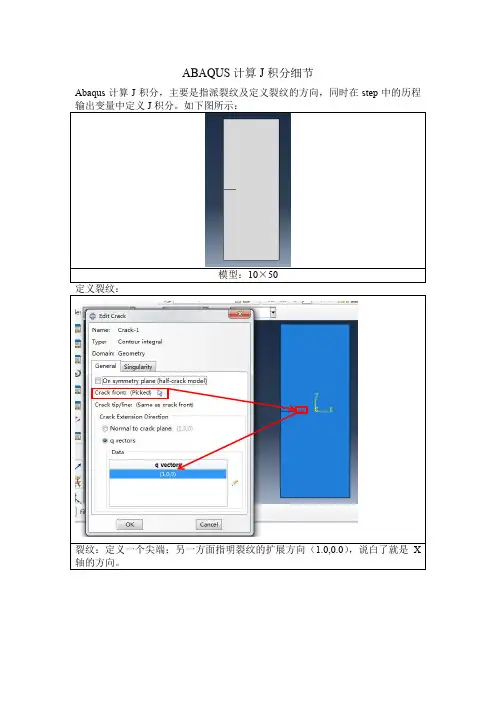
ABAQUS计算J积分细节Abaqus计算J积分，主要是指派裂纹及定义裂纹的方向，同时在step中的历程模型：10×50裂纹：定义一个尖端；另一方面指明裂纹的扩展方向（1.0,0.0），说白了就是X积分数值,图中输入10，则输出10个J积分值计算包含裂纹尖端的包络区域的面积即为J积分避开裂纹尖端塑形区域的不可计算的特性。

同时J积分的计算数值与积分路径无从以上图例可以看出J积分数值区域稳定。

疑问：为何计算多个积分点，是否最后的稳定数值就是需要计算的J积分数值？J积分应该是数值，而不是多个不同的数值。

我个人觉得最后的稳定数值应该是需要计算的积分数值。

从dat文件到inp文件，找到积分区域。

pickseted12以及pickseted13都是节点4，坐标如图所示，在cad模型中的位置如箭头指向，即裂纹尖端。

详细的需要看一下abaqus帮助文档，关于J积分的计算细节。

积分点的个数的意义我还没有搞清楚。

对于应力强度因子K，表征裂纹尖端受力的一个参量，在裂纹尖端的应力场的一定范围内，不同的节点计算数值大体是相同的。

计算应力强度因子：可以利用abaqus直接输出，也可以利用公式计算应力强度因子，以下为利用有限元法计算应力强度因子：计算应力强度因子：从上图可以看出，计算应力强度应力的点与计算J积分的点是一致的。

Abaqus计算的应力强度因子为裂尖处的应力强度因子。

下面我们利用有限元法计算y=0处的应力强度因子，最后外推到裂尖处的应力强度因子。

选取不同的半Abaqus计算J积分注意事项：(1)一、Interaction模块1.1 预制裂纹（步骤：菜单/special/crack/assign seam）注意：并不是作裂纹分析都要定义seam，如果你的裂纹不是一条缝，而是一个缺口，则不需要assign seam，直接走下一步（定义裂纹）就行。

1.2 创建裂纹（步骤：菜单/special/crack/create，type：contour integral）—crack front：crack front是用来定义第一围线积分的区域，2D下我们可以选择包围裂尖点的面，3D则选择包围裂尖线的面；另外还有一种定义crack front的方法，就是直接选择裂尖点（2D）或裂尖线3D），用这个方法定义crack front不需要再定义下一步的crack tip/line，比较简便，两种方法算出的结果没有明显的差别，其实只是影响积分路线的问题，但是J积分值是路径无关的，看个人喜好吧—crack tip/line：这个比较好理解就是裂尖点（2D）或线（3D），如果我们在上一步中用方法二定义crack front，这一步就直接跳过了—crack extension direction（定义裂纹扩展方向）：这里定义的其实是一个虚拟的裂纹扩展方向，定义了这个参考方向后，我们才能通过输出的角度判断裂纹扩展方向，可以通过两种方法：（1）q vector：输入一个方向，用来作为计算裂纹的扩展方向的参考方向；（2）normal to crack plane：crack plane表示裂纹的对称面（当裂纹在一个平面内时，可能需要分开定义多个裂纹），这种方法下我们只需定义裂纹面的法线方向，通过（t表示裂纹尖端的切线）, 会在每个节点得出一个q方向；（3）注意：q的方向对输出的应力强度因子，J积分等都会有影响，一般情况下，q最好在裂纹平面内，且垂直于裂尖线的切线，否则算出的应力强度因子，J积分值等等在不同围线积分中会差别较大。

A B A Q U S 反复加载卸载应力应变计算说明1、 塑性模型采用Armstrong and Frederick model (AF 模型)[1] （1） 屈服准则（Mises 屈服）屈服函数为2)~~(:)~~(23Y s s F ---=αα 式中：s ~为应力偏量，α~为总背应力，Y 为屈服极限 （2） 流动准则（the associated flow rule ）式中：pε~为塑性应变对时间的微分，λ 为待定量[2]，σ~为应力张量 （3） 硬化准则<1> p h i i p i i )()()()(~~32~αζεα-= 式中：)(~i α为背应力分量对时间的微分；)(i h ，)(i ζ为材料常数为已知量，p为等效塑性应变对时间的微分。

<2> )1()(1)(0pMi i i e r Y Y ζ-=-+=∑式中：Y 为对应于等效塑性应变p 的屈服极限，0Y 为初始屈服极限为已知量，)(i r 为材料常数为已知量。

2、 反复加载卸载应力应变计算过程说明假设在受载前，物体的初始应力、应变以及背应力均为零 2.1加载过程计算<1> 外力不足以使得物体中的任何一点的Mises 应力值大于屈服极限此时：塑性应变、背应力均保持为零，屈服极限保持不变。

应力由e e D εσ~:~~~=计算，总应变值等于弹性应变。

<2> 外力使得物体中的任何一点的Mises 应力值大于屈服极限为了说明ABAQUS 是如何确定应变增量1~+∆n ε，有必要对ABAQUS 求解材料非线性问题进行简单介绍[3]。

ABAQUS 首先将载荷分为若干个微小增量，如图1所示。

当结构收到一个微小增量P ∆时，ABAQUS 用与初始结构位移相对应的初始刚度矩阵0K 和载荷增量P ∆计算出结构在这一增量后的位移修正a c 、修正后的位移值a u 和相应的新的刚度矩阵a K 。

ABAQUS 用新的刚度矩阵计算结构的内力a I ，载荷P 和a I 的差值为迭代的残余力a R 。

------------------------------------------------------------------------------------------------------- 如何使用ABAQUS计算应力强度因子Simwefanhj（fanhjhj@）2011.9.9------------------------------------------------------------------------------------------------------- 问题描述：以无限大平板含有一贯穿裂纹为例，裂纹长度为10mm（2a），在远场受双向均布拉应力σ＝100N/mm2。

按解析解，此I型裂纹计算出的应力＝396.23（N.mm-3/2）强度因子πσaK=I以下为使用ABAQUS6.10的计算该问题的过程。

第一步：进入part模块①建立平板part（2D Planar;Deformation;shell），平板的尺寸相对于裂纹足够大，本例的尺寸为100×50（mm）。

②使用Partation Face:sketch工具，将part分隔成如图1形式。

图1第二步：进入property模块①建立弹性材料；②截面选择平面问题的solid，homogeneous；③赋予截面。

第三步：进入Assembly模块不详述。

需注意的是：实体的类型（instance type）选择independent。

第四步：进入mesh模块除小圈内使用CPS6单元外，其它位置使用CPS8单元离散（图2）。

裂纹尖端的奇异在interaction模块中（图4）考虑。

图2第五步：进入interaction模块①指定裂纹special/creak/assign seam，选中示意图3中的黄色线，done！②生成裂纹crack 1，special/crack/create,name：crack 1，type: contour integral.当提示选择裂纹前端时，选则示意图的红圈区域，当提示裂纹尖端区域时选择红圈的圆心，用向量q表示裂纹扩展方向（示意图3绿色箭头）。

abaqus中le计算方法abaqus中的le计算方法引言：在工程设计和科学研究中，常常需要对材料的力学性能进行分析和评估。

有限元分析方法是一种常用的工具，可以通过数值模拟的方式来计算结构的应力和变形等力学参数。

而abaqus软件则是一款常用的有限元分析软件，具有强大的计算能力和广泛的应用范围。

其中，le计算方法是abaqus中一种重要的分析方法，本文将对其原理和应用进行详细介绍。

一、le计算方法的原理le计算方法是abaqus中一种基于拉伸试验数据进行弹性模量和屈服强度计算的方法。

其原理主要包括以下几个步骤：1. 数据输入：首先需要准备拉伸试验数据，包括应力-应变曲线和应变的计算方法。

这些数据可以通过实验测量获得，也可以通过材料的力学性能参数进行估计。

2. 材料模型的选择：根据实际情况，选择合适的材料模型来描述材料的力学性能。

常用的材料模型包括线性弹性模型和非线性弹性模型等。

3. 弹性模量的计算：根据拉伸试验数据和选定的材料模型，可以通过拟合方法计算材料的弹性模量。

拟合方法可以是最小二乘法或其他数学方法。

4. 屈服强度的计算：根据拉伸试验数据和选定的材料模型，可以通过拟合方法计算材料的屈服强度。

拟合方法可以是最小二乘法或其他数学方法。

5. 结果输出：最后，将计算得到的弹性模量和屈服强度输出到abaqus软件中，用于后续的有限元分析。

二、le计算方法的应用le计算方法在工程设计和科学研究中具有广泛的应用。

以下是一些常见的应用场景：1. 材料评估：通过le计算方法可以对不同材料的力学性能进行评估。

例如，可以比较不同材料的弹性模量和屈服强度，选择合适的材料用于特定的工程应用。

2. 结构分析：le计算方法可以用于预测结构在不同载荷情况下的应力和变形。

通过将计算得到的弹性模量和屈服强度输入到abaqus 软件中，可以进行更加准确的有限元分析。

3. 材料改进：通过le计算方法可以评估不同处理方式对材料力学性能的影响。

ABAQUS计算J积分细节Abaqus计算J积分，主要是指派裂纹及定义裂纹的方向，同时在step中的历程输出变量中定义J积分。

如下图所示：模型：10×50定义裂纹：裂纹：定义一个尖端；另一方面指明裂纹的扩展方向（1.0,0.0），说白了就是X轴的方向。

Step中输出裂纹参量：积分数值,图中输入10，则输出10个J积分值J积分的理解：计算包含裂纹尖端的包络区域的面积即为J积分尖端塑形区域的不可计算的特性。

同时J积分的计算数值与积分路径无关。

以下为六个计算从以上图例可以看出J积分数值区域稳定。

疑问：为何计算多个积分点，是否最后的稳定数值就是需要计算的J积分数值？J积分应该是数值，而不是多个不同的数值。

我个人觉得最后的稳定数值应该是需要计算的积分数值。

从dat文件到inp文件，找到积分区域。

pickseted12以及pickseted13都是节点4，坐标如图所示，在cad模型中的位置如箭头指向，即裂纹尖端。

详细的需要看一下abaqus帮助文档，关于J积分的计算细节。

积分点的个数的意义我还没有搞清楚。

对于应力强度因子K，表征裂纹尖端受力的一个参量，在裂纹尖端的应力场的一定范围内，不同的节点计算数值大体是相同的。

计算应力强度因子：可以利用abaqus直接输出，也可以利用公式计算应力强度因子，以下为利用有限元法计算应力强度因子：计算应力强度因子：从上图可以看出，计算应力强度应力的点与计算J积分的点是一致的。

Abaqus计算的应力强度因子为裂尖处的应力强度因子。

下面我们利用有限元法计算y=0处的应力强度因子，最后外推到裂尖处的应力强度因子。

选取不同的半径r值计算得到的应力Abaqus计算J积分注意事项：(1)一、Interaction模块(2) 1.1 预制裂纹（步骤：菜单/special/crack/assign seam）(3)注意：并不是作裂纹分析都要定义seam，如果你的裂纹不是一条缝，而是一个缺口，则不需要assign seam，直接走下一步（定义裂纹）就行。

断裂与损伤力学应力强度因子数值计算方法综述2013年6月第一章应力强度因子求解方法概述含有裂纹的工程结构的断裂力学分析一直是一个重要问题，在断裂力学理论中应力强度因子是线弹性断裂力学中最重要的参量。

它是由构件的尺寸、形状和所受的载荷形式而确定。

由于裂尖应力场强度取决于应力强度因子，因此在计算各种构件或试件的应力强度因子是线弹性断裂力学的一项重要任务。

由于应力强度因子在裂纹体分析中的中心地位，它的求解自断裂力学问世以来就受到了高度的重视。

迄今为止，已经产生了众多的理论和致值解法。

70年代中期以前的有关工作在文献中已有相当全面的总结，近20年来，求解的方法又得刭了明显的发展与完善。

下文将穿透裂纹问题(二维)与部分穿透裂纹问题（三维）分开讨论。

第二章 二维裂纹问题2.1 复变函数法由Muskhelishvili 的复变函数法，应力函数为：_])()()([2/1)]()(Re[z z z z z z z z χψψχψ++=+=Φ平面应变情况下的应力与位移为： )]('Re[42222z yx y x ϕφφσσ=∂∂+∂∂=+ )]('')(''[22z z z i xy y x χϕτσσ+=+-)](')('[21)(243x z z z iv u χϕμϕμμ+--=+ 可以证明，在裂纹尖端区域：)]('lim[220z z z iK K K I ϕπ-=-=∏由上式可见。

由于k 仅与)(z φ有关，因此只需确定一个解析函数)(z φ，就能求得k I ，这一方法一般只能用来解无限体裂纹问题。

对于含孔边裂纹的无限大板，通常可利用复变函数的保角映射原理来简化解题过程。

如采用复变（解析）变分方法，则可求解具有复杂几何形状的含裂纹有限大板的应力强度因子。

2.2 积分方程法弹性边值问题可以变为求解下列形式的积分方程：)())(()().,(r f dt t b a t t P t r M -=--⎰ 由积分方程解出沿裂纹的坐标的函数，便能直接求出应力强度因子k 。

基于ABAQUS的复杂裂纹应力强度因子的研究摘要：在实际工程领域，裂纹问题一直都是一个影响结构安全性的难题。

本文从现实工程角度出发，针对复杂裂纹的断裂破坏机理，采用基于ABAQUS的数值模拟技术，进行了深入的研究。

为了证明采用数值模拟技术研究复杂裂纹的可靠性，本文首先利用ABAQUS对其他学者做出的理论值进行了验证，结果表明理论和数值具有高度的吻合性。

然后进行了复杂裂纹在不同情况下的裂尖应力强度因子进行了研究。

从而为现实工程建设中一些不便于实验研究的复杂情况，提出了研究的可行性方法，具有较强的实践意义。

关键词：裂纹；应力强度因子；ABAQUS；数值模拟0 引言断裂力学是研究带裂纹体的强度和裂纹扩展规律的一门学科。

断裂力学的最早理论可以追溯到1920年，为了研究玻璃、陶瓷等脆性材料的实际强度比理论强度低的原因，Griffith[1-2]提出了在材料中存在裂纹的设想，而Irwin[3-4]在1957年提出了应力强度因子以及其后形成的断裂韧度的概念后，断裂力学理论出现了重大的突破，奠定了线弹性断裂力学的基础。

当前国内外许多学者[5-8]已将多裂纹问题作为主攻方向，但是受到诸多条件的制约，目前并未取得明显的成果。

1复杂裂纹研究的现实依据图（a）是位于四川的几大主要断裂带的分布图，在宏观上形成了V型的断层结构。

汶川Ms8.0级地震，就是龙门山断裂带在构造应力场长期作用下，积累的应变能突然释放的结果。

图（b）是2002年11月3日，阿拉斯加中部迪纳利断层发生了一次M w7.9级地震。

从图（b）可以看出三条主断裂层形成了典型的的分支结构，究断层的性质对于预知、了解地质作用，估计可能发生的破坏具有重要参考价值。

图1 现实V型、Y型裂纹存在模型2 Y型裂纹的应力强度因子研究2.1有限元建模中间带有裂纹的双轴压缩试件，如图2所示，在相关断裂力学的试验分析中被广泛应用。

故此，本文以此典型试件作为研究对象，进行数值模拟计算。

应力强度因子的数值计算方法引言一、理论计算方法1.弹性理论解法弹性理论解法是应力强度因子计算中最常用的一种方法。

它假设材料是弹性线性的，并忽略了材料的塑性变形。

常用的解法有Westergaard解和Westergaard-Hankel解。

2.能量解法能量解法是一种基于弹性力学的解法，通过计算裂纹尖端处的应力场能量和应变能量来计算应力强度因子。

常用的解法有Line-spring法和Irwin法。

3.有限元法有限元法是一种数值计算方法，通过将复杂的问题离散化为多个小区域，并在每个小区域上建立适当的数学模型进行计算。

通过求解离散化的方程组，可以得到裂纹尖端处的应力强度因子。

有限元法可以处理各种复杂的边界条件和几何形状的问题，并且可以考虑非线性和塑性变形。

这使得它成为计算应力强度因子的一种重要方法。

二、实验计算方法实验计算方法主要是通过设计和进行试验来测量裂纹尖端区域的应力和应变场，然后根据测量数据计算应力强度因子。

常用的方法有：1.发光全场法发光全场法是一种全场应变测量技术，通过在被测结构表面涂覆一层发光材料，然后利用高速摄像机记录结构在加载过程中的应变分布。

通过分析图像数据，可以得到裂纹尖端区域的应力和应变场，进而计算应力强度因子。

2.特征裂纹法特征裂纹法是一种利用疲劳试验得到应力强度因子的方法。

通过在试样上开几何形状确定的裂纹，然后在加载过程中观察裂纹的扩展行为，通过测量裂纹长度和加载荷载的关系，可以计算应力强度因子。

3.数值模拟法数值模拟法是一种将实验和数值计算相结合的方法。

通过建立几何和材料特性相似的数值模型，并在模型中模拟加载过程，可以得到裂纹尖端区域的应力和应变场，进而计算应力强度因子。

三、应力强度因子的应用1.疲劳断裂评估基于应力强度因子的计算结果，可以对工程结构在疲劳载荷下的断裂寿命进行评估和预测。

这对于提高结构的可靠性和安全性具有重要意义。

2.材料断裂韧性评定3.裂纹扩展行为研究通过分析应力强度因子的变化规律，可以研究裂纹在不同加载条件下的扩展行为，揭示断裂的机理和规律。