2018中考总复习知识点梳理：第10讲一次函数(华师大版)

华师大版八年级数学下《函数及其图像》知识点归纳一．变量与函数1 ．函数的定义：一般的，在某个变化过程中有两个变量x和y，对于x的每一个数值y都有唯一的值与之对应，我们说x叫做自变量，y叫做因变量，y叫做x的函数。

2．自变量的取值范围：（1）能够使函数有意义的自变量的取值全体。

（2）确定函数自变量的取值范围要注意以下两点：一是使自变量所在的代数式有意义；二是使函数在实际问题中有实际意义。

（3）不同函数关系式自变量取值范围的确定：①函数关系式为整式时自变量的取值范围是全体实数。

②函数关系式为分式时自变量的取值范围是使分母不为零的全体实数。

③函数关系式为二次根式时自变量的取值范围是使被开方数大于或等于零的全体实数。

3 ．函数值：当自变量取某一数值时对应的函数值。

这里有三种类型的问题：（1）当已知自变量的值求函数值就是求代数式的值。

（2）当已知函数值求自变量的值就是解方程。

（3）当给定函数值的一个取值范围，欲求自变量的取值范围时实质上就是解不等式或不等式组。

二．平面直角坐标系：1．各象限内点的坐标的特征：（1）点p（x,y）在第一象限→x＞0,y＞0.（2）点p（x,y）在第二象限→x＜0,y＞0.（3）点p（x,y）在第三象限→x＜0,y＜0（4）点p（x,y）在第四象限→x＞0,y＜0.2 ．坐标轴上的点的坐标的特征：（1）点p（x,y）在x轴上→x为任意实数，y=0（2）点p（x,y）在y轴上→x=0,y为任意实数3 ．关于x轴，y轴，原点对称的点的坐标的特征：（1）点p（x,y）关于x轴对称的点的坐标为（x,-y）.（2）点p（x,y）关于y轴对称的点的坐标为（-x,y）.（3）点p（x,y）关于原点对称的点的坐标为（-x,-y）4 ．两条坐标轴夹角平分在线的点的坐标的特征：（1）点p（x,y）在第一、三象限夹角平分在线→x=y.（2）点p（x,y）在第二，四象限夹角平分在线→x+y=05．与坐标轴平行的直线上的点的坐标的特征：（1）位于平行于x轴的直线上的所有点的纵坐标相同。

初二数学一次函数华东师大版【本讲教育信息】一. 教学内容：§18.3 一次函数二. 重点、难点：1. 重点：⑴体会一次函数的意义，•理解一次函数与正比例函数的联系和区别；⑵会画一次函数的图象，了解一次函数图象与正比例函数图象之间的位置关系； ⑶掌握一次函数的性质．2. 难点：⑴用待定系数法求一次函数的解析式；⑵运用一次函数的图象和性质解决简单的实际问题．三. 知识梳理：1. 一次函数用自变量的一次式表示的函数叫一次函数．由定义可知：形如y ＝kx ＋b （k ≠0，k 、b 为常数），则y 是x 的一次函数．一次函数可以表示为y ＝kx ＋b （k ≠0，k 、b 为常数），特别地，当b ＝0时，形如y ＝kx （k ≠0，k 为常数）的一次函数叫做正比例函数．正比例函数总可以表示为y ＝kx （k ≠0，k 为常数）．2. 一次函数的图象：⑴一次函数的图象特征：一次函数y ＝kx ＋b （k ，b 是常数，k ≠0）的图象经过点)0,kb ( 和点（0，b ）的一条直线．正比例函数y ＝kx （k 是常数，k ≠0）的图象是经过点（0，0）和（1，k ）的一条直线． 直线y ＝kx 与y ＝kx ＋b （k ≠0）的位置关系：当b>0时，直线y ＝kx ＋b 可由直线y ＝kx （k ≠0）沿y 轴向上平移b 个单位长度而得；当b<0时，直线y ＝kx ＋b 可由y ＝kx （k ≠0）沿y 轴向下平移|b|个单位长度而得．⑵一次函数图象的性质：k 值 函数的图象及性质k ＞0 y 随x 的增大而增大k ＜0y 随x 的增大而减小3. 待定系数法及一次函数的应用先设出式子中的未知系数，再根据条件求出未知系数，从而写出这个式子的方法叫做待定系数法．其中未知的系数也叫做待定系数．用待定系数法求函数解析式的一般步骤：⑴写出函数解析式的一般形式；⑵把已知条件（通常是自变量和函数的对应值或函数图象上某点的坐标等）代入函数解析式中，得到关于待定系数的方程或方程组．⑶解方程或解方程组求出待定系数的值，从而写出函数解析式．4. 一次函数图象与二元一次方程和一元一次不等式的关系【典型例题】例1.判断下列函数中，哪些y 是x 的一次函数？哪些y 是x 的正比例函数？⑴y ＝－x ＋1； ⑵11-=x y ； ⑶x y 3=； ⑷231+-=xy ； ⑸2x ＋3y ＝5； ⑹xy ＝4； ⑺12+=x y .分析：根据一次函数和正比例函数的定义来解答此题．解：⑴y ＝x ＋1 ，⑶x y 3=，⑸2x ＋3y ＝5中y 都是x 的一次函数，其中x y 3=，又是正比例函数．例2. 在同一坐标系中画下列函数的图象：⑴y ＝2x ＋4；⑵y ＝2x ．并回答：①两直线有何位置关系？②直线y ＝2x ＋4是由y ＝2x 经怎样平移而得？分析：函数y ＝2x ＋4与y ＝2x 的图象都可用描点法描两个点而画出来．解：⑴由y ＝2x ＋4知直线过（0，4）和（－2，0）两点；（2）由y ＝2x 知直线过原点和（1，2）两点，这两个函数的图象如下图：由图象可知：①直线y ＝2x ＋4与y ＝2x 互相平行．②直线y ＝2x ＋4可由直线y ＝2x 沿y 轴向上平移4个单位长度而得．例3. （2006·新疆）如下图，把直线l 向上平移2个单位得到直线l ’，则l ’的表达式为（ ）A. y ＝21x ＋l C. y ＝21x —lB. y ＝－21x 一1 D. y ＝一21x ＋1分析：两直线平行则k的值相同，向上平移2个单位，只需将原解析式常数项加2即可．解：选D．例4. 等腰三角形的周长为20cm，求底边长y cm与腰长x cm的函数关系式，并画出图象．分析：求实际问题的函数关系式，就是列y与x的方程，再加以变形整理．因为实际问题的自变量取值有一定的限制，所以画出的图象只能是其中的一部分．解：根据题意，得y＝20－2x（5＜x＜10）其图象是过（5，10）和（10，0）两点的线段，如下图所示．例5. 已知y＋m与x＋n成正比例（m、n为常数）：⑴试说明y是x的一次函数；⑵若x＝－3时，y＝5；x＝2时，y＝2．求函数关系式．分析：（1）要说明y是x的—次函数，就要说明y与x满足形如y＝kx＋b（k≠0，k、b为常数）的关系式．而题目中已知y＋m与x＋n成正比例，便可以设y＋m＝k（x＋n）（k ≠0，k为常数），加以变形整理，便可得到y＝kx＋kn－m的形式，其中是k≠0，k、n、m 为常数，从而说明y是x的一次函数⑵由⑴可知，y是x的一次函数，我们就可以设解析式为y＝px＋q（p≠0，p、q为常数）代入已知条件，得p、q的方程，从而求出p、q，进而求出解析式．解：⑴设y＋m＝k（x＋n）（k≠0，k为常数），则y＝kx＋kn－m因为其中是k≠0，k、m、n为常数，所以y是x的一次函数．⑵因为y是x的一次函数，故设y＝px＋q（p≠0，p、q为常数）．根据题意，得⎩⎨⎧+=+-=,22,35q p q p 解得之 ⎪⎪⎩⎪⎪⎨⎧=-=51653q p 所以函数关系式为51653+-=x y ．例6. 一次函数的图象过（3，0），且与坐标轴所围成的图形的面积为9，求一次函数的函数关系式．分析：题目已知了一个点的坐标，要求解析式还需根据另一条件“图象与两坐标轴所围成的三角形面积为9”去求出另一个点的坐标，注意另一个点的坐标的两种情况．解：设一次函数的图象与x 轴交于A （3，0），与y 轴交于B （0，b ），则OA ＝3，OB ＝｜b ｜又因为 9=∆AOB S ，所以921=⋅⋅OB OA ， 即：9321=⋅⋅b ，解得：b ＝±6 所以B 的坐标为（0，6）或（0，－6）设一次函数的解析式为y ＝kx ＋b （k ≠0，k 、b 为常数），则⎩⎨⎧+==bk b 306 或 ⎩⎨⎧+==-bk b 306 解之得 ⎩⎨⎧=-=62b k 或 ⎩⎨⎧-==62b k 所以一次函数的解析式是y ＝－2x ＋6或y ＝2x －6．例7. 如图，一次函数y ＝kx ＋b 与y ＝kbx 的图象在同一平面直角坐标系里，正确的是（ ）分析：解这类题的关键是从能确定每个待定系数的符号的函数入手．可以根据正比例函数确定k、b的正负情况再看一次函数的图象是否符合．解：选B．例8. 已知：点（2，m）和（－3，n）都在直线y＝－3x＋1上，试比较m和n的大小，你能想出几种判断的方法？分析：思路一：分别求出m和n的值．思路二：根据一次函数的增减性比较．思路三：画出图象草图，把（2，m）、（－3，n）描出来再比较．解：方法一：根据题意，得m＝－3×2＋1＝－5n＝－3×（－3）＋1＝10所以m<n方法二：在y＝－3x＋1中，因为是k＝－3<0所以y随x增大而减小，而2>－3所以m<n方法三：如下图所示是直线y＝－3x＋1的示意图，由图象可知：m<n．例9. 已知点A（2，2）、B（－4，3）：⑴在y轴上求一点P，使PA＋PB最短；⑵在X轴上求一点Q，使QA＋QB最短．分析：⑴如图1所示，连结AB交y轴于点P，由几何知识可知点P就是使PA＋PB最短的点，因此，我们可先求出直线AB的解析式，再求出它与y轴的交点．⑵如图2所示，画点B关于x轴的对称点B＇，连结AB＇交x轴于Q，由几何知识可知，点Q就是使QA＋QB最短的点．要求这一点的坐标，就是要求直线AB，与x轴的交点坐标，可先求出直线AB＇的解析式，已知A的坐标，只需再求出B＇，而B＇与B关于x轴对称，且B（－4，3），所以B＇（－4，－3）．解：（1）连结AB 交y 轴于P ，设直线AB 解析式为y ＝kx ＋b （k ≠0，k 、b 为常数），根据题意得⎩⎨⎧+=+-=b k b k 2243解之得⎪⎪⎩⎪⎪⎨⎧=-=3761b k 所以直线AB 的解析式为3761+-=x y ． 由x ＝0，得37=y ， 所以⎪⎭⎫ ⎝⎛37,0P ．（2）如图2，画B 关于x 轴的对称点B '，则点B '为（－4，－3），连B A '交x 轴于Q ．设直线B A '的解析式为y ＝mx ＋n （m ≠0，m 、n 为常数），则 ⎩⎨⎧+=+-=-n m n m 22.43，解之得⎪⎪⎩⎪⎪⎨⎧==3165n m 所以直线B A '的解析式为3165+=x y 令y ＝0，则52-=x 所以Q 的坐标为（52-，0）．【模拟试题】（答题时间：40分钟）一. 选择题：1.直线y ＝－2x ＋3是由y ＝－2x －1怎样平移而得的 （ ）A. 沿y 轴向上平移4个单位长度B. 沿y 轴向下平移3个单位长度C. 沿y 轴向上平移3个单位长度D. 沿y 轴向下平移4个单位长度2. ()5612++-=m x m y m 是关于x 的一次函数，则m 的值为（ ） 图1图2A. －1或1B. 1C. －1D. ±l 或65- 3. 正比例函数图象过（－3，1），则解析式为 （ ）A. y ＝－3xB. x y 31-=C. x y 3-=D. xy 3= 4. 直线y ＝2x ＋3不经过第（ ）象限．A. 一B. 二C. 三D. 四5. 点（－1，2）在下列哪条直线上 （ ）A. y ＝2xB. y ＝－2x ＋1C. y ＝－2xD. x y 21-= 6. 如图，y ＝k （x －1）与y ＝kx 在同一坐标系中图象正确的是 （ ）二. 填空题：7. 直线y ＝3x ＋6与坐标轴围成的三角形的面积是____________．8. y ＝kx ＋b 中k>0，b ＜0，则图象不经过第________象限．9. 已知一次函数y ＝－x ＋2的图象与x 轴交于点A ，与y 轴交于点B ．则△AOB 的形状是____________三角形．10. y ＝5x －10中y 随x 增大而______________．三. 解答题：11. 一次函数y ＝kx ＋b ，当－3≤x ≤1时，对应的y 的值为1≤y ≤9，则kb 的积为多少？12. 已知一次函数y ＝kx ＋k －1，当k 是取什么实数时：（1）图象过原点；（2）图象过点（2，1）；（3）图象过一、三、四象限；（4）图象与y 轴的交点在x 轴下方；（5）y 随x 增大而增大．13. 已知一次函数的图象与坐标轴所围成的三角形的面积为12，且过（0，4）．求一次函数的解析式．14. 已知矩形的周长为40cm ，求一边长y （cm ）与另一边长x （cm ）[注：它们是相邻两边]的函数关系式，并作出函数的图象．【试题答案】一.选择题。

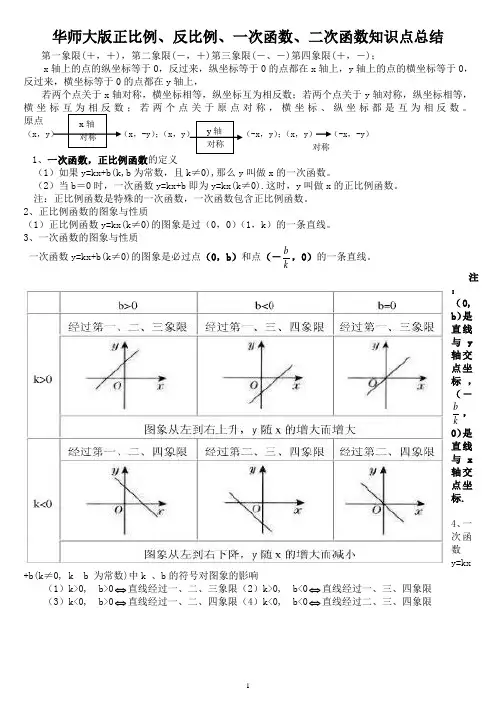
华师大版正比例、反比例、一次函数、二次函数知识点总结第一象限(＋，＋)，第二象限(－，＋)第三象限(－、－)第四象限(＋，－)；x 轴上的点的纵坐标等于0，反过来，纵坐标等于0的点都在x 轴上，y 轴上的点的横坐标等于0，反过来，横坐标等于0的点都在y 轴上，若两个点关于x 轴对称，横坐标相等，纵坐标互为相反数；若两个点关于y 轴对称，纵坐标相等，横坐；若两个点关于原点对称，横坐标、纵坐标都是互为相反数。

原点 （x ，y x ，-y ）；（x ，y -x ，y ）；（x ，y ） （-x ，-y ） 对称1、一次函数，正比例函数的定义（1）如果y=kx+b(k,b 为常数，且k ≠0),那么y 叫做x 的一次函数。

（2）当b ＝0时，一次函数y=kx+b 即为y=kx(k ≠0).这时，y 叫做x 的正比例函数。

注：正比例函数是特殊的一次函数，一次函数包含正比例函数。

2、正比例函数的图象与性质（1）正比例函数y=kx(k ≠0)的图象是过（0，0）（1，k ）的一条直线。

3、一次函数的图象与性质一次函数y=kx+b(k ≠0)的图象是必过点（0，b ）和点（－kb，0）的一条直线。

注：（0,b ）是直线与y 轴交点坐标，（－k b ，0）是直线与x 轴交点坐标. 4、一次函数y=kx+b(k ≠0, k b 为常数)中k 、b 的符号对图象的影响（1）k>0, b>0⇔直线经过一、二、三象限（2）k>0, b<0⇔直线经过一、三、四象限 （3）k<0, b>0⇔直线经过一、二、四象限（4）k<0, b<0⇔直线经过二、三、四象限5、对一次函数y=kx+b 的系数k, b 的理解。

（1）k(k ≠0)相同，b 不同时的所有直线平行，即直线l 1:y=k 1x+b 1；直线l 2:y=k 2x+b 2( k 1，k 2均不为零，k 1，b 1，k 2， b 2为常数)k 1=k 2 l 1∥l 2平行 k 1=k 2 l 1与l 2重合 b 1≠b 2 b 1=b 2（2）k(k ≠0)不同，b 相同时的所有直线恒过y 轴上一定点（0,b ），例如：直线y=2x+3, y=-2x+3, y=21x+3均交于y 轴一点（0，3）6、直线的平移：所谓平移，就是将一条直线向左、向右（或向上，向下）平行移动，平移得到的直线k 不变，直线沿y 轴平移多少个单位，可由公式︱b 1－b 2︱得到，其中b 1，b 2是两直线与y 轴交点的纵坐标，直线沿x 轴平移多少个单位，可由公式︱x 1－x 2︱求得，其中x 1，x 2是由两直线与x 轴交点的横坐标。