线性规划模型在企业生产计划中的应用
- 格式:doc
- 大小:294.50 KB
- 文档页数:17

线性规划的应用1. 引言线性规划是一种优化问题的数学建模工具,广泛应用于经济、工程、运输、资源分配等领域。
本文将探讨线性规划在生产计划、供应链管理和投资组合优化中的应用。
2. 生产计划中的线性规划应用生产计划是企业核心业务之一,通过合理的生产计划可以提高生产效率和降低成本。
线性规划可以帮助企业确定最佳的生产计划,以满足市场需求并最大化利润。
例如,假设一家制造公司有多个产品需要生产,每个产品的生产成本、销售价格和市场需求量都不同。
通过线性规划模型,可以确定每个产品的生产数量,以最大化总利润。
3. 供应链管理中的线性规划应用供应链管理是企业与供应商、生产商和分销商之间协调和优化物流和信息流的过程。
线性规划可以用于优化供应链中的物流和库存管理。
例如,一家零售公司需要决定每个仓库的库存水平和重新补充货物的频率,以最大程度地满足顾客需求并最小化库存成本。
通过线性规划模型,可以确定最佳的库存水平和补货策略。
4. 投资组合优化中的线性规划应用投资组合优化是金融领域中的一个重要问题,即如何选择一组资产以最大化收益并控制风险。
线性规划可以用于确定最佳的投资组合权重。
例如,一个投资者有多个可选的资产,每个资产有不同的预期收益率和风险。
通过线性规划模型,可以确定每个资产的权重,以最大化整体投资组合的预期收益并控制风险。
5. 结论线性规划是一种强大的数学工具,可以应用于各种优化问题中。
本文讨论了线性规划在生产计划、供应链管理和投资组合优化中的应用。
通过合理的模型建立和求解,可以帮助企业和个人做出最佳决策,提高效益和竞争力。

线性规划在制定企业生产计划中的应用作者:方利来源:《商业文化》2012年第02期摘要:本文旨在针对有限的人力、时间和原材料等资源条件的约束下,使用线性规划模型来制定生产计划以实现企业利润最大化,同时利用软件LINGO 8.0求解线性规划模型并分析在各类所需资源变动下对该模型所产生的影响并寻找最优生产方案。
关键词:生产计划;数学模型;线性规划;LINGO8.0中图分类号:F224 文献标识码:A 文章编号:1006-4117(2012)02-0052-02线性规划(Linear Programming)无论从理论和方法的成熟性,还是从运用的广泛性,都是运筹学中极具有应用价值的一个重要分支。
它在农业、工业、服务业、军事、运输和计划管理等多方面都越来越受重视、越来越得到广泛的运用。
随着高科技电子计算机的求解软件的不断发展,专门用来解决线性规划问题的LINGO软件已经可以解决成千上万个约束条件和变量大规模复杂问题,该软件的出现使得解决线性规划问题已变得得心应手。
线性规划方法是研究在有限的原材料、人力、时间、资金、设备等资源条件下,如何进行资源的优化配置和最佳生产计划,使企业达到最好的经济效益(利润最大、产量最多、效用最高)。
下面将应用线性规划法对企业如何制定产品生产计划的问题进行深入的探讨。
一、线性规划的模型线性规划模型的建立需要以下两个条件:一是最优目标。
问题需要完成的目标可以用线性函数来描述并能够使用最大值或最小值来进行表示;二是约束条件。
这些限制条件可以用决策变量的线性方程组或线性不等式来表示,为达到目标函数的最佳值提供限制约束。
通常线性规划的数学模型一般可以表示成如下所示:其中式(1)称为目标函数,式(2)称为约束条件。
在线性规划模型中称Z为目标函数;称xj(j=1,2,…,n)为决策变量;称cj(j=1,2,…,n)为目标函数系数或价值系数;称bj(j=1,2,…,m)为资源约束常数或简称右端项;称aij(j=1,2,…,m;j=1,2,…,n)为约束系数或技术系数。
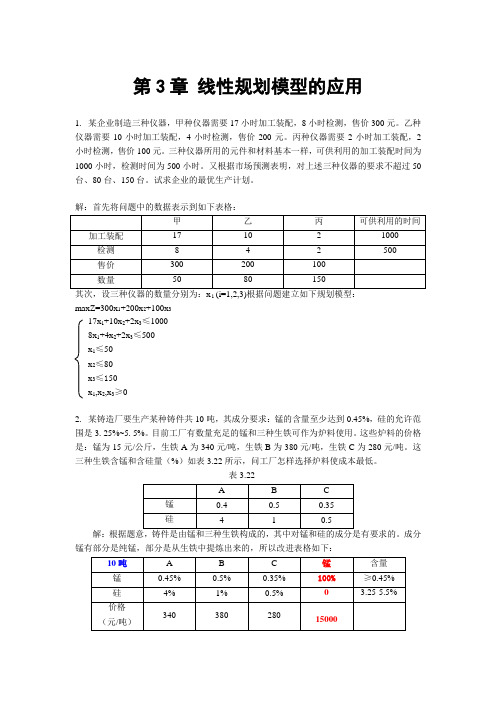
第3章线性规划模型的应用1.某企业制造三种仪器,甲种仪器需要17小时加工装配,8小时检测,售价300元。
乙种仪器需要10小时加工装配,4小时检测,售价200元。
丙种仪器需要2小时加工装配,2小时检测,售价100元。
三种仪器所用的元件和材料基本一样,可供利用的加工装配时间为1000小时,检测时间为500小时。
又根据市场预测表明,对上述三种仪器的要求不超过50台、80台、150台。
试求企业的最优生产计划。
解:首先将问题中的数据表示到如下表格:imaxZ=300x1+200x2+100x317x1+10x2+2x3≤10008x1+4x2+2x3≤500x1≤50x2≤80x3≤150x1,x2,x3≥02. 某铸造厂要生产某种铸件共10吨,其成分要求:锰的含量至少达到0.45%,硅的允许范围是3.25%~5.5%。
目前工厂有数量充足的锰和三种生铁可作为炉料使用。
这些炉料的价格是:锰为15元/公斤,生铁A为340元/吨,生铁B为380元/吨,生铁C为280元/吨。
这三种生铁含锰和含硅量(%)如表3.22所示,问工厂怎样选择炉料使成本最低。
表3.22成分锰有部分是纯锰,部分是从生铁中提炼出来的,所以改进表格如下:设铸件中含有三种生铁和锰的量分别为xi(i=1,2,3,4)吨,则数学模型如下:maxZ=340x1+380x2+280x3+15000x4x1+x2+x3+x4=100.45%x1+0.5%x2+0.35%x3+x4≥0.45%*104%x1+1%x2+0. 5%x3≥3.25%*104%x1+1%x2+0. 5%x3≤5.5%*10xi≥0(i=1,2,3,4)3. 某工厂要做100套钢架,每套用长为2.9m,2.1m和1.5m的圆钢各一根。
已知原料每根长7.4m,问应如何下料,可使所用原料最省。
解:4. 绿色饲料公司生产雏鸡、蛋鸡、肉鸡三种饲料。
这三种饲料是由A、B、C三种原料混合而成。
产品的规格要求、产品单价、日销售量、原料单价见表3.23、表3.24。

线性规划的应用引言概述:线性规划是一种优化问题的数学建模方法,可以用于解决许多实际问题。
本文将探讨线性规划在不同领域的应用,包括生产计划、资源分配、运输问题、金融投资和市场营销等。
一、生产计划1.1 产能规划:线性规划可以匡助企业确定最优产能规划,通过最大化产量和最小化成本,实现生产效益的最大化。
1.2 原材料采购:线性规划可以优化原材料的采购计划,确保原材料的供应充足,同时最小化采购成本。
1.3 生产调度:线性规划可以匡助企业制定最佳的生产调度方案,合理安排生产过程,提高生产效率和产品质量。
二、资源分配2.1 人力资源:线性规划可以匡助企业合理分配人力资源,根据不同部门和岗位的需求,确定最佳的人员配置方案。
2.2 设备调度:线性规划可以优化设备的调度计划,确保设备的利用率最大化,减少闲置时间和能源浪费。
2.3 资金分配:线性规划可以匡助企业合理分配资金,根据不同项目的需求,确定最佳的资金分配方案,实现资金的最大效益。
三、运输问题3.1 物流配送:线性规划可以优化物流配送路线,确定最佳的配送方案,减少运输成本和时间。
3.2 仓储管理:线性规划可以匡助企业优化仓储管理,确定最佳的仓储位置和库存量,减少库存成本和仓储空间的浪费。
3.3 运输调度:线性规划可以匡助企业制定最佳的运输调度计划,合理安排运输车辆和货物的装载,提高运输效率和减少运输成本。
四、金融投资4.1 资产配置:线性规划可以匡助投资者确定最佳的资产配置方案,平衡风险和收益,实现投资组合的最优化。
4.2 资金规划:线性规划可以优化资金的规划和运用,确保资金的最大化利用和最小化风险。
4.3 投资决策:线性规划可以匡助企业制定最佳的投资决策方案,根据不同项目的收益和风险,确定最优的投资方向。
五、市场营销5.1 定价策略:线性规划可以匡助企业确定最佳的定价策略,根据市场需求和成本考虑,确定最优的价格水平。
5.2 促销策略:线性规划可以优化促销策略,确定最佳的促销活动方案,提高产品销售量和市场份额。


线性规划的应用引言概述:线性规划是一种数学优化方法,用于解决线性约束条件下的最优化问题。
它在许多领域都有广泛的应用,包括生产计划、资源分配、运输问题等。
本文将详细介绍线性规划的应用,并分为五个部分进行阐述。
一、生产计划的优化1.1 生产成本最小化:线性规划可用于确定生产计划,以最小化生产成本。
通过设定生产量的变量和成本的约束条件,可以得到最优的生产计划。
1.2 资源分配优化:线性规划可以帮助确定资源的最优分配,以满足生产需求。
通过考虑资源的供应量和需求量,可以得出最佳的资源分配方案。
1.3 生产效率提升:线性规划可以优化生产过程,提高生产效率。
通过考虑生产线上的各个环节和资源的利用率,可以得出最佳的生产安排,从而提升生产效率。
二、运输问题的解决2.1 最优运输方案:线性规划可用于解决运输问题,以确定最佳的运输方案。
通过考虑运输成本、运输量和运输距离等因素,可以得出最优的运输方案。
2.2 供应链优化:线性规划可以优化供应链的运作,以提高运输效率和降低成本。
通过考虑供应商、生产商和分销商之间的关系和需求,可以得出最佳的供应链优化方案。
2.3 库存管理:线性规划可用于优化库存管理,以最小化库存成本和满足需求。
通过考虑库存量、订购量和供应量等因素,可以得出最佳的库存管理方案。
三、资源分配问题的解决3.1 人力资源优化:线性规划可以优化人力资源的分配,以满足不同部门和项目的需求。
通过考虑人员的技能、工作量和工作时间等因素,可以得出最佳的人力资源分配方案。
3.2 资金分配优化:线性规划可用于优化资金的分配,以最大化利润或最小化成本。
通过考虑不同项目的收益和成本,可以得出最佳的资金分配方案。
3.3 能源利用优化:线性规划可以优化能源的利用,以提高能源效率和降低能源成本。
通过考虑不同能源的供应量和需求量,可以得出最佳的能源利用方案。
四、市场营销策略的制定4.1 定价策略优化:线性规划可用于优化产品定价策略,以最大化利润或市场份额。
线性规划在工商管理中的应用
一、引言
线性规划是一种数学优化方法,可以帮助在给定约束条件下找到最优解,其在工商管理中有着广泛的应用。
本文将探讨线性规划在工商管理中的具体应用情况。
二、供应链管理中的线性规划应用
供应链管理是工商管理中一个重要的领域,线性规划可以帮助优化供应链中的货物流动和库存管理。
通过优化运输路线和库存水平,企业可以降低成本,提高效率。
三、生产计划中的线性规划应用
线性规划可以帮助企业制定最优生产计划,平衡生产能力和市场需求之间的关系。
通过合理安排生产资源和生产顺序,企业可以实现生产成本最小化和生产效率最大化。
四、营销策略中的线性规划应用
在制定营销策略时,线性规划可以帮助企业确定最优的销售推广方式和渠道选择,以最大化收益。
通过考虑市场需求和销售成本等因素,企业可以制定更具有效果的营销策略。
五、人力资源管理中的线性规划应用
线性规划在人力资源管理中也有着重要的应用,例如员工排班和资源分配等方面。
通过线性规划方法,企业可以合理安排员工工作时间和工作任务,以提高员工效率和满足企业需求。
六、财务管理中的线性规划应用
在财务管理中,线性规划可以帮助企业进行财务规划和资金管理。
通过优化投资组合和资金分配,企业可以实现财务风险的最小化和资金利用效率的最大化。
结论
综上所述,线性规划在工商管理中有着广泛的应用,可以帮助企业优化决策和提高经营效率。
在实际运营中,企业可以结合线性规划方法,制定更科学合理的管理策略,从而实现经济效益的最大化。
浅谈线性规划在实际生活中的应用随着计算机技术的发展,线性规划(Linear Programming,LP)已被广泛应用于科学理论和实际生活中。
LP的出现使得工程师们能够快速的解决复杂的实际问题,使得各种优化事件在时间上有很大的优势。
本文将探讨线性规划在实际生活中的应用。
首先,线性规划可以用于企业的生产规划,以实现企业的目标以及降低成本。
要达到此目的,企业需要根据相关因素,如生产量、市场需求、库存水平、机器等,制定最佳生产计划。
例如,一家企业可以用线性规划来解决库存控制问题。
同时,企业还可以使用线性规划来进行工资管理、资产配置等,实现企业成本最低化。
其次,线性规划可以用于交通系统的路径规划。
线性规划可以解决交通运输问题,如最优路径规划、最短路径规划,以及交通系统的容量调度等。
例如,在城市交通系统中,可以使用LP来解决最优路径问题,以帮助出行者在拥堵的状态下,尽快到达目的地。
此外,线性规划还可以用于个人理财规划,以优化个人投资组合。
通过线性规划,个人理财者可以根据自己的风险偏好,使用资金最优化分配,即考虑投资组合中的收益、风险和成本等因素。
同时,也可以利用LP模型,结合投资者的利率偏好、投资期限等因素,探索个人最优投资组合。
此外,线性规划还可以用于建筑物的设计。
例如,可以使用LP 模型来优化财务计划,以确定最佳建筑设计,并考虑在建设过程中可能出现的各种问题。
另外,LP也可以用于求解土地利用、城市综合规划等问题。
最后,LP也可以用于自然资源的有效利用。
LP模型可以用于最佳利用公共资源,如水、电、矿产等,达到最大利益的若干目标。
此外,LP模型也可以用于环境污染的减排、森林的保护、植物的种植等,确保自然资源的可持续发展。
综上所述,线性规划在实际生活中有着广泛的应用,可以有效地解决复杂的实际问题。
但是,在实际应用中,也存在一定的局限性,像非线性问题这类更加复杂的问题就不能使用LP来求解。
因此,未来需要在 LP模型和非线性模型之间进行技术上的结合,以解决更多实际问题。
诚信声明我声明,所呈交的毕业论文是本人在老师指导下进行的研究工作及取得的研究成果。
据我查证,除了文中特别加以标注和致谢的地方外,论文中不包含其他人已经发表或撰写过的研究成果,我承诺,论文中的所有内容均真实、可信。
毕业论文作者签名:签名日期:年月日摘要:在企业生产过程中,生产资源的分配直接影响到企业的经济效益。
因此,企业在制定生产计划时,人力物力和时间等资源的优化配制是首要面对的关键问题,而建立线性规划模型则是目前解决该问题的有效方法之一。
本文旨在针对上述有限资源条件的约束下,通过建立相应的线性规划模型来制定生产计划以实现企业资源最优化、利益最大化,同时利用LINGO 11.0软件求解线性规划模型并分析在某些资源变动时对该模型所产生的影响并寻求最优生产方案。
关键词:企业生产计划;线性规划;数学模型;LINGO 11.0Abstract:In the enterprise production process, the allocation of production resources directly affects the economic efficiency of enterprises. Therefore, enterprises in the development of production plan, formulated to optimize the resources of manpower and time is the key problem of face. And to establish the linear programming model is one of the effective ways to solve the problem. This paper aimed at the limited resource constraints, by establishing linear programming model corresponding to make production plan in order to realize the maximization of enterprise resource optimization, interest, and using LINGO11.0 software to solve the linear programming model and analysis the influence on the model in some resource changes and seek the optimal production plan.Key words:Production plan;Linear programming;Mathematical model;LINGO 11.0目录1.线性规划问题概述 (1)1.1线性规划问题的基本概念 (1)1.2 线性规划方法的应用范围与求解的基本步骤 (1)1.3 线性规划模型的基本概念 (2)1.4 建立线性规划模型的一般步骤 (2)1.5 线性规划模型的求解方法 (3)2.线性规划在企业生产计划中的应用 (3)2.1 线性规划在企业生产计划中应用的背景 (3)2.2 把线性规划运用到企业生产中的作用和意义 (4)2.3 针对企业生产计划模型的分析 (4)2.4建立生产计划决策分析的线性规划模型 (5)2.5 案例及相关分析 (5)3.总结 (11)参考文献 (12)致谢 (13)线性规划模型在企业生产计划中的应用1.线性规划问题概述1.1线性规划问题的基本概念线性规划是运筹学中,研究较早、发展较快、应用较多、方法较成熟的一个重要分支,也是最基本部分,它是辅助人们进行科学管理的一种数学方法。
自1947年丹捷格提出了一般线性规划问题求解的方法---单纯形法之后,线性规划在理论上趋向成熟,在实际中日益广泛与深入。
特别是在电子计算机能处理成千上万个约束条件和决策的线性规划问题之后,线性规划的适用领域更为广泛了。
它所研究的问题主要有两类:一类是当一项任务确定后,如何统筹安排,尽量做到以最少的人力、物力资源去完成任务;另一类是对已有的人力、物力资源,如何安排使用,并完成任务的。
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题。
满足线性约束条件的解叫做可行解,由所有可行解组成的集合叫做可行域。
由此,我们给出线性规划的一般定义如下:①求一组变量X j(j=1,2,3,…,n)的值,使之满足关于这组变量的若干个线性等式或不等式的约束条件,并使这组变量的一个线性函数取得极值(极小或极大),其中,这些变量称为决策变量,所要优化的函数称为目标函数,此类问题称为“线性规划”(Linear Programming,简记LP)问题。
其中,决策变量、约束条件和目标函数是线性规划的三要素。
1.2 线性规划方法的应用范围与求解的基本步骤②(1)线性规划方法的应用范围,可以用一种归纳性的叙述加以概括为:凡是能用线性约束方程(等式或者不等式)组描述其内部运行规则,且有明确的线性优化目标的问题,都可以用线性规划的方法求解。
无论这些问题属于哪个领域,只要能满足上述条件,都属于线性规划方法的应用范围。
比如一些常见的领域有:企业营销策划、产品生产计划、采购与库存管理、物流管理、理财与投资、人事管理、系统综合评价、工程设计优化、宏观经济运行调控、城市管理、作战规划等。
(2)求解线性规划问题的基本步骤可以总结如下:①提出并抽象问题②建立数学模型③求解④检验解⑤解的灵敏度分析⑥解的回归①钱辰,李姝.线性规划方法在企业生产中的应用[J].中国高新技术企业,2011,(3)42.②高红卫,线性规划方法应用详解 [M],北京,科学出版社,2004.12-15.1.3 线性规划模型的基本概念线性规划问题的模型是由一组含有等式、不等式的代数方程以及一个具有求极值关系的目标函数(优化函数)表达式构成的复合式抽象数学模型。
(1)线性规划模型的构成需要具备以下条件:① 需要求解的问题所包含的每一种资源数量都是确定的,而且每个决策变量也都是确定的,其取值范围也是已知的,并且问题所包含的每一种决策变量与相关资源之间的约束关系、不同决策变量对于某一种资源的需求之和与该资源的现有总量的对应关系(用≤,=,≥之一来表示)都是确定的。
② 存在一个确定的、期望达到的目标(极大或极小值),并且这个目标可用对全部或部分决策变量与相关价值(费用)系数乘积之和(称为目标函数)来表达。
(2)线性规划模型的一般形式如下:③目标函数 n n x c x c x c z +++=…(min)max2211 (1) 约束条件2222212111212111),(),(b x a x a x a b x a x a x a n n n n ≥=≤+++≥=≤+++… … … … (2) m n m n m m b x a x a x a ),(2211≥=≤+++0,,,21≥n x x x (一般为非负性)其中,j c (j=1,2,…,n) 称为价值(费用)系数或目标函数系数。
j x (j=1,2,…,n )称为决策变量的非负约束条件,若其取值范围为 (-∞,+∞)时,则称为任意变量(无约束变量)。
j b (j=1,2,…,n )称为资源常数或简称约束右端系。
ij a ( i=1,2,…,m ;j=1,2,…,n )称为技术系数或约束系数。
1.4 建立线性规划模型的一般步骤 建立数学模型是解线性规划问题的第一步,也是关键的一步。
一个好的数学模型必须对问题的系统及其同内外部环境的关系进行概括,根据实际需要提的出问题,进行求解。
由上述可知,如何确定决策变量、约束条件和目标函数是解决线性规划问题模型的关键。
具体的建立步骤如下: ① 根据已知条件设置决策变量。
即寻找所要求解或间接求解的未知数并用j x (j=1,2,…,n )表示出来。
③孙庭锋.浅析线性规划在企业生产计划中的应用[J].商业经济, 2006. (276):18.②确定目标函数。
用上面所确定的变量建立一个线性函数(此处为一次函数),再根据具体问题明确是求目标函数的极大值或是极小值。
③确定资源常量并找出决策变量之间的关系及其与资源约束常量之间的关系,建立等式或不等式线性方程。
④确定决策变量的取值范围。
⑤整理所得到的代数表达式,形成规范的线性规划数学模型。
1.5 线性规划模型的求解方法线性规划模型建立之后就需要求出个决策变量的最优解以及目标函数的最优值。
经过几十年的发展,其解法多样并且逐渐成熟。
当决策变量个数比较少时比较常用图解法,即直接根据约束条件在坐标轴上画出可行域并找出最优解。
而目前求解线性规划问题的基本方法是单纯行法。
它需要将模型的一般形式变换成标准形式后再运用矩阵的计算方式得到最优解。
为了提高解题速度,又有改进单纯形法、对偶单纯形法、原始对偶方法、分解算法和各种多项式时间算法。
现有的计算机软件基本上是利用上述方法的原理。
例如:Excel、MATLAB、LINDO和LINGO等软件。
本文后面的案例主要运用软件LINGO 11.0进行求解、分析。
2.线性规划在企业生产计划中的应用2.1 线性规划在企业生产计划中应用的背景随着经济全球化的不断发展,企业之间的竞争与合作也日渐成熟与激烈,企业必须不断提高盈利水平,增强其获利能力。
即如何应用最小的资源成本获得最大的利益永远是企业发展的核心目的。
只有在生产、销售、新产品研发等一系列过程中发挥自己的优势,提高企业效率,降低成本,形成企业的核心竞争力,才能在激烈的竞争中立于不败之地。
因此根据市场的需求有计划的生产变成为其必不可少的手段之一,特别是在资源有限的情况下。
而实践证明,线性规划模型是制定企业生产计划行之有效地重要方法。
过去很多企业在生产、运输、市场营销等方面没有利用线性规划方法进行合理的配置,从而增加了企业的生产负担,使企业的利润不能达到最大化。
在竞争日益激烈的今天,如果还按照过去的方式,无疑是会被淘汰的,所以就有必要利用线性规划的知识对战略计划、生产、销售各个环节进行优化从而降低生产成本,提高企业的效率。
此外线性规划问题在农业、工业、服务业、军事、运输和计划管理等多方而都越来越受重视、越来越得到广泛的运用。
所以运用线性规划知识统筹企业的生产计划是大势所趋、是合理的。
本文中笔者试图通过线性规划具体模型的建立并用计算机软件求解结果,以及对相关参数的分析,阐述线性规划是解决企业生产计划问题的一个有效方法。
2.2 把线性规划运用到企业生产中的作用和意义把线性规划的知识运用到企业生产中去,可以使企业适应市场激烈的竞争,能够及时、准确、科学、有效地制定生产计划、投资计划以及对资源进行合理配置。