下载文档原格式
第一章答案1.3计算以下程序中x=x+1的语句频度for(i=1;i<=n;i++)for(j=1;j<=i;j++)for(k=1;k<=j;k++)x=x+1;【解答】x=x+1的语句频度为：T(n)=1+(1+2)+〔1+2+3〕+……+〔1+2+……+n〕=n(n+1)(n+2)/61.4试编写算法，求p n(x)=a0+a1x+a2x2+…….+a n x n的值p n(x0),并确定算法中每一语句的执行次数和整个算法的时间复杂度，要求时间复杂度尽可能小，规定算法中不能使用求幂函数。
注意：此题中的输入为a i(i=0,1,…n)、x和n,输出为P n(x0)。
算法的输入和输出采用以下方法〔1〕通过参数表中的参数显式传递〔2〕通过全局变量隐式传递。
讨论两种方法的优缺点，并在算法中以你认为较好的一种实现输入输出。
【解答】〔1〕通过参数表中的参数显式传递优点：当没有调用函数时，不占用存，调用完毕后形参被释放，实参维持，函数通用性强，移置性强。
缺点：形参须与实参对应，且返回值数量有限。
〔2〕通过全局变量隐式传递优点：减少实参与形参的个数，从而减少存空间以及传递数据时的时间消耗缺点：函数通用性降低，移植性差算法如下：通过全局变量隐式传递参数PolyValue(){ int i,n;float x,a[],p;printf(“\nn=〞);scanf(“%f〞,&n);printf(“\nx=〞);scanf(“%f〞,&x);for(i=0;i<n;i++)scanf(“%f 〞,&a[i]); /*执行次数：n次*/p=a[0];for(i=1;i<=n;i++){ p=p+a[i]*x; /*执行次数：n次*/x=x*x;}printf(“%f〞,p);}算法的时间复杂度：T(n)=O(n)通过参数表中的参数显式传递float PolyValue(float a[ ], float x, int n){float p,s;int i;p=x;s=a[0];for(i=1;i<=n;i++){s=s+a[i]*p; /*执行次数:n次*/p=p*x;}return(p);}算法的时间复杂度：T(n)=O(n)第二章答案2.7试分别以不同的存储构造实现单线表的就地逆置算法，即在原表的存储空间将线性表〔a1,a2,…,a n〕逆置为(a n,a n-1,…,a1)。
第1章绪论习题一、问答题1.什么是数据结构？2.四类基本数据结构的名称与含义。
3.算法的定义与特性。
4.算法的时间复杂度。
5.数据类型的概念。
6.线性结构与非线性结构的差别。
7.面向对象程序设计语言的特点。
8.在面向对象程序设计中，类的作用是什么？9.参数传递的主要方式及特点。
10.抽象数据类型的概念。
二、判断题1.线性结构只能用顺序结构来存放，非线性结构只能用非顺序结构来存放。
2.算法就是程序。
3.在高级语言（如C、或 PASCAL）中，指针类型是原子类型。
三、计算下列程序段中X=X+1的语句频度for(i=1;i<=n;i++)for(j=1;j<=i;j++)for(k=1;k<=j;k++)x=x+1;[提示]：i=1时： 1 = (1+1)×1/2 = (1+12)/2i=2时： 1+2= (1+2)×2/2 = (2+22)/2i=3时： 1+2+3= (1+3)×3/2 = (3+32)/2…i=n时：1+2+3+……+n= (1+n)×n/2 = (n+n2)/2f(n) = [ (1+2+3+……+n) + (12 + 22 + 32 + …… + n2 ) ] / 2=[ (1+n)n/2 + n(n+1)(2n+1)/6 ] / 2=n(n+1)(n+2)/6=n3/6+n2/2+n/3区分语句频度和算法复杂度：O(f(n)) = O(n3)四、试编写算法求一元多项式Pn(x)=a0+a1x+a2x2+a3x3+…a n x n的值P n(x0)，并确定算法中的每一语句的执行次数和整个算法的时间复杂度，要求时间复杂度尽可能的小，规定算法中不能使用求幂函数。
注意：本题中的输入a i(i=0,1,…,n), x和n，输出为P n(x0).通常算法的输入和输出可采用下列两种方式之一：（1）通过参数表中的参数显式传递；（2）通过全局变量隐式传递。
算法分析与设计教程习题解答第1章 算法引论1. 解：算法是一组有穷的规则，它规定了解决某一特定类型问题的一系列计算方法。
频率计数是指计算机执行程序中的某一条语句的执行次数。
多项式时间算法是指可用多项式函数对某算法进行计算时间限界的算法。
指数时间算法是指某算法的计算时间只能使用指数函数限界的算法。
2. 解：算法分析的目的是使算法设计者知道为完成一项任务所设计的算法的优劣，进而促使人们想方设法地设计出一些效率更高效的算法，以便达到少花钱、多办事、办好事的经济效果。
3. 解：事前分析是指求出某个算法的一个时间限界函数（它是一些有关参数的函数）；事后测试指收集计算机对于某个算法的执行时间和占用空间的统计资料。
4. 解：评价一个算法应从事前分析和事后测试这两个阶段进行，事前分析主要应从时间复杂度和空间复杂度这两个维度进行分析；事后测试主要应对所评价的算法作时空性能分布图。
5. 解：①n=11； ②n=12； ③n=982； ④n=39。
第2章 递归算法与分治算法1． 解：递归算法是将归纳法的思想应用于算法设计之中，递归算法充分地利用了计算机系统内部机能，自动实现调用过程中对于相关且必要的信息的保存与恢复；分治算法是把一个问题划分为一个或多个子问题，每个子问题与原问题具有完全相同的解决思路，进而可以按照递归的思路进行求解。
2． 解：通过分治算法的一般设计步骤进行说明。
3． 解：int fibonacci(int n) {if(n<=1) return 1;return fibonacci(n-1)+fibonacci(n-2); }4. 解：void hanoi(int n,int a,int b,int c) {if(n>0) {hanoi(n-1,a,c,b); move(a,b);hanoi(n-1,c,b,a); } } 5. 解：①22*2)(−−=n n f n② )log *()(n n n f O =6． 解：算法略。
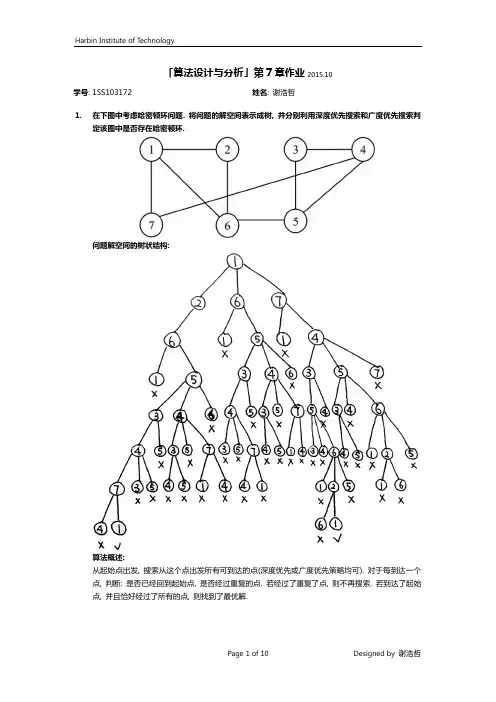
「算法设计与分析」第7章作业2015.10学号: 15S103172 姓名: 谢浩哲1.在下图中考虑哈密顿环问题. 将问题的解空间表示成树, 并分别利用深度优先搜索和广度优先搜索判定该图中是否存在哈密顿环.问题解空间的树状结构:算法概述:从起始点出发, 搜索从这个点出发所有可到达的点(深度优先或广度优先策略均可). 对于每到达一个点, 判断: 是否已经回到起始点, 是否经过重复的点. 若经过了重复了点, 则不再搜索. 若到达了起始点, 并且恰好经过了所有的点, 则找到了最优解.算法实现:深度优先搜索:35}广度优先搜索:!isVisited(startPoint, i,372.考虑8-魔方问题. 分别用深度优先算法, 广度优先算法, 爬山法, 最佳优先方法判定上图所示的初始格局能够通过一系列操作转换成目标格局, 将搜索过程的主要步骤书写清楚.问题的部分解空间树状结构:深度优先搜索:搜索顺序为1 -> 2 -> 4 -> 10 -> …广度优先搜索:搜索顺序为1 -> 2 -> 3-> 4 -> 5 -> 6 -> …爬山法:基于深度优先搜索, 选取当前分支上最优解;搜索顺序为1 -> 2 -> 4 -> 11 -> …最佳优先方法:基于深度优先搜索, 选取所有分支上最优解;搜索顺序为1 -> 2 -> 4 -> 11 -> …3.分别使用深度优先法和分支限界法求解子集和问题的如下实例.输入: 集合S=7, 4, 6, 13, 20, 8和整数K=18.输出: S’使得S’中元素之和等于K.深度优先搜索:问题的部分解空间如下如所示:算法实现:分枝限界法可以在深度优先搜索时进行必要的剪枝, 例如对于分支7-4. 此时的分支上的和为11, 因此该分支上的数最大不可能超过18 - 11 = 7. 因此可见, 在深度优先搜索中搜索的13和8这两个分支其实可以进行剪枝. 其他分支亦然.算法实现:只需将以上代码的17行替换为:if ( !isSelected[i] &&4.将任意一整数n划分为若干整数之和的划分, 并按照降序的序列输出出来, 例如5的划分为: 5, 4+1,3+2, 3+1+1, 2+2+1, 2+1+1+1, 1+1+1+1+1.问题解空间的树状图:算法实现(深度优先搜索):import java.util.ArrayList;public List<List<Integer>> getSplit(int n,1725 List<Integer> newSplit =new ArrayList<Integer>(currentSplit);5.在一个一维空间上有n个点1, 2, 3, 4, …, n, 有一个粒子它初始位置为1, 粒子从初始位置1开始做随机运动, 方向只有左右两个, 每次运动结束该粒子就会移动到相邻的位置上. 已知该粒子在i(1<i<n)点位置上向左运动的概率为p i, 该粒子在1点只能向右运动, 在n点只能向左运动, 那么请问该粒子在t次运动后它最有可能出现在哪个点上, 以及输出该粒子向右运行距离的期望值.对于n=5的问题解空间的树状图:算法实现(广度优先搜索):15public Queue<Point> getFinalPositions(25q.offer(new Point(cp.coordinate + 1,31 q.offer(new Point(cp.coordinate - 1,cp.probability * p[cp.coordinate]));。
第1章绪论习题一、问答题1. 什么是数据结构？2. 四类基本数据结构的名称与含义。
3. 算法的定义与特性。
4. 算法的时间复杂度。
5. 数据类型的概念。
6. 线性结构与非线性结构的差别。
7. 面向对象程序设计语言的特点。
8. 在面向对象程序设计中，类的作用是什么？9. 参数传递的主要方式及特点。
10. 抽象数据类型的概念。
二、判断题1. 线性结构只能用顺序结构来存放，非线性结构只能用非顺序结构来存放。
2. 算法就是程序。
3. 在高级语言（如C、或PASCAL）中，指针类型是原子类型。
三、计算下列程序段中X=X+1的语句频度for(i=1;i<=n;i++)for(j=1;j<=i;j++)for(k=1;k<=j;k++)x=x+1;[提示]：1/2 = = (1+12)/2i=1时：1 = (1+1)×1/22/2 = = (2+22)/2i=2时：1+2= (1+2)×2/23/2 = = (3+32)/2i=3时：1+2+3= (1+3)×3/2…n/2 = = (n+n2)/2i=n时：1+2+3+……+n= (1+n)×n/2f(n) = [ (1+2+3+……+n) + (12 + 22 + 32 + …… + n2 ) ] / 2=[ (1+n)n/2 + n(n+1)(2n+1)/6 ] / 2请浏览后下载，资料供参考，期待您的好评与关注！=n(n+1)(n+2)/6=n3/6+n2/2+n/3区分语句频度和算法复杂度：O(f(n)) = O(n3)四、试编写算法求一元多项式Pn(x)=a0+a1x+a2x2+a3x3+…a n x n的值P n(x0)，并确定算法中的每一语句的执行次数和整个算法的时间复杂度，要求时间复杂度尽可能的小，规定算法中不能使用求幂函数。
注意：本题中的输入a i(i=0,1,…,n), x和n，输出为Pn(x)通常算法的输入和输出可采用下列两种方式之一：法的输入和输出可采用下列两种方式之一：（1）通过参数表中的参数显式传递；（2）通过全局变量隐式传递。
5..证明等式gcd(m,n)=gcd(n,m mod n)对每一对正整数m,n都成立.Hint:根据除法的定义不难证明:●如果d整除u和v, 那么d一定能整除u±v;●如果d整除u,那么d也能够整除u的任何整数倍ku.对于任意一对正整数m,n,若d能整除m和n,那么d一定能整除n和r=m mod n=m-qn；显然，若d能整除n和r，也一定能整除m=r+qn和n。
数对(m,n)和(n,r)具有相同的公约数的有限非空集，其中也包括了最大公约数。
故gcd(m,n)=gcd(n,r)6.对于第一个数小于第二个数的一对数字,欧几里得算法将会如何处理?该算法在处理这种输入的过程中,上述情况最多会发生几次?Hint:对于任何形如0<=m<n的一对数字,Euclid算法在第一次叠代时交换m和n, 即gcd(m,n)=gcd(n,m)并且这种交换处理只发生一次.7.a.对于所有1≤m,n≤10的输入, Euclid算法最少要做几次除法?(1次)b. 对于所有1≤m,n≤10的输入, Euclid算法最多要做几次除法?(5次)gcd(5,8)习题1.21.(农夫过河)P—农夫W—狼G—山羊C—白菜2.(过桥问题)1,2,5,10---分别代表4个人, f—手电筒4. 对于任意实系数a,b,c, 某个算法能求方程ax^2+bx+c=0的实根,写出上述算法的伪代码(可以假设sqrt(x)是求平方根的函数)算法Quadratic(a,b,c)//求方程ax^2+bx+c=0的实根的算法//输入:实系数a,b,c//输出:实根或者无解信息D←b*b-4*a*cIf D>0temp←2*ax1←(-b+sqrt(D))/tempx2←(-b-sqrt(D))/tempreturn x1,x2else if D=0 return –b/(2*a)else return “no real roots”else //a=0if b≠0 return –c/belse //a=b=0if c=0 return “no real numbers”else return “no real roots”5.描述将十进制整数表达为二进制整数的标准算法a.用文字描述b.用伪代码描述解答：a.将十进制整数转换为二进制整数的算法输入：一个正整数n输出：正整数n相应的二进制数第一步：用n除以2，余数赋给Ki(i=0,1,2...)，商赋给n第二步：如果n=0，则到第三步，否则重复第一步第三步：将Ki按照i从高到低的顺序输出b.伪代码算法DectoBin(n)//将十进制整数n转换为二进制整数的算法//输入：正整数n//输出：该正整数相应的二进制数，该数存放于数组Bin[1...n]中i=1while n!=0 do {Bin[i]=n%2;n=(int)n/2;i++;}while i!=0 do{print Bin[i];i--;}9.考虑下面这个算法,它求的是数组中大小相差最小的两个元素的差.(算法略) 对这个算法做尽可能多的改进.算法MinDistance(A[0..n-1])//输入:数组A[0..n-1]//输出:the smallest distance d between two of its elements习题1.31.考虑这样一个排序算法,该算法对于待排序的数组中的每一个元素,计算比它小的元素个数,然后利用这个信息,将各个元素放到有序数组的相应位置上去.a.应用该算法对列表‖60,35,81,98,14,47‖排序b.该算法稳定吗?c.该算法在位吗?解:a. 该算法对列表‖60,35,81,98,14,47‖排序的过程如下所示:b.该算法不稳定.比如对列表‖2,2*‖排序c.该算法不在位.额外空间for S and Count[]4.(古老的七桥问题)习题1.41.请分别描述一下应该如何实现下列对数组的操作,使得操作时间不依赖数组的长度. a.删除数组的第i 个元素(1<=i<=n)b.删除有序数组的第i 个元素(依然有序) hints:a. Replace the i th element with the last element and decrease the array size of 1b. Replace the ith element with a special symbol that cannot be a value of the array ’s element(e.g., 0 for an array of positive numbers ) to mark the i th position is empty. (―lazy deletion ‖)第2章 习题2.17.对下列断言进行证明:(如果是错误的,请举例) a. 如果t(n )∈O(g(n),则g(n)∈Ω(t(n)) b.α>0时,Θ(αg(n))= Θ(g(n)) 解:a. 这个断言是正确的。
