缓和曲线坐标计算公式 (1)

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

查看文章高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式2009年06月29日星期一21:57高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式分享给好友高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

缓和曲线坐标计算公式：
S=L-(L5)/(90×R2×K2)◢ B= L2×180/(6×R×K×π)◢ Q=W＋B◢X=U＋S×CosQ◢ Y=V＋S×SinQ◢
其中：L为缓和曲线起点至计算桩号的弧长，R为缓和曲线后接圆曲线的半径，K为缓曲线总长，W为缓和曲线起点的切线方位角，U为缓和曲线起点的X坐标，V为缓和曲线起点的Y坐标。

左转角半径为负，右转角为正。

圆曲线坐标计算公式：
B=K×90/(R×π)+L×180/(R×π)◢ Q=K/2-(K×K2)/(240×R2)◢P=K2/(24×R)◢ M=R×SinB+Q◢N= R×(1- CosB)+P◢
E=tan-1 (N/M)◢ F=∫(M2+N2 )◢ T=W+E◢X=U+F×CosT◢Y=V+F×SinT◢∫：开根号
K为缓和曲线总长，R为圆曲线半径，L为圆曲线起点至计算点的弧长，W为缓和曲线起点的切线方位角，U为缓和曲线起点的坐标，V 为缓和曲线起点的坐标.
左转角半径为负，右转角为正。

查看文章高速公路线路(缓和曲线、竖曲线、圆曲线、匝道坐标计算公式2009年06月29日星期一21:57高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：丨②圆曲线的半径：R③缓和曲线的长度：10④转向角系数：K(1或一1⑤过ZH点的切线方位角：a⑥点ZH的坐标：xZ, yZ计算过程：〔14 = (——)X吩3361SI?⑵一丄十」^40RH 3456R%(3]dt = arctg —+n-180[4)-------------------------- S= J盂十y：匸[血二①+口-河(SJ KJ= Scosci^⑺齐=Ssin(\旧丘=Xt+Xr[9]y=说明：当曲线为左转向时，K=1，为右转向时，K=-1 ,公式中n的取值如下：<0弧<0>0n = 0n = 2n=1n = 1当计算第二缓和曲线上的点坐标时，贝U: l为到点HZ的长度a为过点HZ的切线方位角再加上180K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：I②圆曲线的半径：R③缓和曲线的长度：I0④转向角系数：K(1或一1⑤过ZH点的切线方位角：a⑥点ZH的坐标：xZ , yZ计算过程：尺兀24R 2688R3[3]m=^-- +―弐—2 240R E Z34560R'阮湎口砂用K15)叭二RsiiiU'十m[6H = arctg —+n- LEO⑺E= J奩+y：[8]a = q+a—go旧]爲=ScosC^(IO]y j—SsinCl^[I U K=石+心0的=班+圻说明：当曲线为左转向时，K=1，为右转向时,K=-1 , 公式中n的取值如下：也：^<0业<oW A 0凭<0y,>o 1y»n = 0n = 2n = 1n = 1当只知道HZ点的坐标时，贝V:l为到点HZ的长度a为过点HZ的切线方位角再加上180K值与知道ZH点坐标时相反xZ, yZ为点HZ的坐标三、曲线要素计算公式1超曲馬任畜占转角fit P 2KM⑵«4段任；■点特用值B ・阻也L. 乂p 严丹）L 2 Rife 2⑶戛一建曲段恳转角跖K ■互 2R⑷第二集曲段总特角仙內•卫 山.里—圧珪II 师口重；阻=!!_ 斗+ _2 240E £ 3456OR⑹第卫對惧秽重5?-里-- +」一2 昭 OK 34b60R阿平移畫5・——\24R 26BBR 3—十—(P L+ P ?卡HR't.—十 mi -4 22 oo®二切线恰n -里卫 止如+p,+2JUt e 5+>2 2M- 2 203晦逅k 慶:Lo =嗣弓（】严®站陡段长度* 1 ■丄L ■仝些Br Pi+p ； Ri+R?⑭雇需曲D 的边缘曲裟檢度：1- Al + Dp公式中各符号说明： l ――任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）11 ――第一缓和曲线长度12 ――第二缓和曲线长度10 ――对应的缓和曲线长度R ――圆曲线半径R1 ――曲线起点处的半径⑻第二平移■眩■ ——5-如 2688K ⑼第一切SiKiT]- ^_5>1R2 ――曲线终点处的半径P1 ――曲线起点处的曲率P2 ――曲线终点处的曲率a ――曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1（上坡为牛”， ② 第二坡度：i2（上坡为 牛”，下坡为③ 变坡点桩号：SZ④ 变坡点高程：HZ⑤ 竖曲线的切线长度：T下坡为-a v[SIR.= 五、超高缓和过渡段的横坡计算⑥待求点桩号：S 计算过程:2T1+—〔[3]H 二吐十L _丄-扌尺仁長已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=（i2-i1（1-3d2+2d3+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：xO, y0⑤曲线起点切线方位角：a0⑥曲线起点处曲率：P0（左转为•”，右转为牛⑦曲线终点处曲率：P1（左转为•”，右转为牛求：①线路匝道上点的坐标：x,y②待求点的切线方位角：aT计算过程：S=K-K,[I ]当已=P J= 0吋IK = Xfl-FScOS^ y=y c+Ssin^ —q.⑵当p严p冲。

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式未知2009-12-27 21:40:34 本站高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”) 求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

缓和曲线坐标计算公式你说的坐标应该是在整条公路上的坐标不是支距法算出来的坐标吧支距法现在都不怎么用了给你个偏角法的计算公式吧ZH至i点的偏角A=30xL的平方除以派除以R 除以LsZH至i点的弦长C=L（ZH至i点的长）-L的5次方除以90 除以R的平方除以Ls的平方具体是这样的：建立以ZH或（HZ）为原点，过ZH的切线及半径分别X轴与Y轴的坐标系统后，就可以用曲线上各点在这个坐标系统中的x，y测设曲线。

坐标计算如下：缓和曲线：xi=li- li^5／40R^2li^2yi=li／6Rl0-li^7／336R^3li^3圆曲线：xi=R×sinαi+myi=R(1-cosαi)+pα=180°∕πR（li- l0）+β0li是曲线上与测设点距ZH点的弧长，l0缓和曲线长度，m，p，β0是缓和曲线参数缓和曲线计算偏角公式L2（平方）/（2RLs）L:缓和曲线上任一点到ZH点距离R：圆半径Ls：缓和曲线长当L=Ls时，公式就是L/(2R)卵形曲线坐标计算方法简介：在高速公路立交平面线型中，现越来越多采用卵形曲线这一线型形式，而卵形曲线坐标的计算在现有相关书籍中却又很少提到，这就为施工中的坐标计算及放样增加了较大难度，为解决此难道，我在实践中通过对缓和曲线坐标的计算加以分析并结合理论知识，总结出了卵形曲线坐标的计算方法和技巧。

关键字：卵形曲线坐标计算一、概念卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

三、坐标计算以雅（安）至攀（枝花）高速公路A合同段（西昌西宁）立交区A匝道一卵形曲线为例，见图一：（图一）已知相关设计数据见下表：主点桩号坐标（m）切线方位角（θ）X Y ° ’ ”ZHAK0+090 9987.403 10059.378 92 17 26.2HY1AK0+160 9968.981 10125.341 132 23 51.6YH1AK0+223.715 9910.603 10136.791 205 24 33.6HY2AK0+271.881 9880.438 10100.904 251 24 18.5YH2AK0+384.032 9922.316 10007.909 337 04 54.2HZAK0+444.032 9981.363 10000.000 0 00 001、缓和曲线（卵形曲线）参数计算A1= =59.161卵形曲线参数：A2=（HY2-YH1）×R1（小半径）×R2（大半径）÷（R2-R1）=（271.881-223.715）×50×75÷（75-50）= 7224.900A2= =84.999A3= =67.0822．卵形曲线所在缓和曲线要素计算卵形曲线长度LF由已知条件知：LF=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度LS，由此找出HZ“点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）LM=LS（YH1至HZ“的弧长）=A2÷R1=7224.900÷50=144.498∴HZ“桩号=YH1+LM=223.715+144.498=368.213LE=HY2至HZ“的弧长=A2÷R2=7224.900÷75=96.332或LE= LM-LF=144.498-48.166=96.332卵形曲线长度LF=LM-LE=144.498-96.332=48.166（校核）HY2=HZ“-LE=368.213-96.332=271.881（校核）由上说明计算正确3．HZ“点坐标计算（见图二）（图二）①用缓和曲线切线支距公式计算，缓和曲线切线支距公式通式：Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义：n —项数序号(1、2、3、……n)！—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算（有关书籍中一般为2-3项，不能满足小半径的缓和曲线计算精度要求，如本例中AK0+090~AK0+160段缓和曲线，如AK0+160中桩坐标带2项算误差达8cm），公式如下：X=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8]- L21÷[7.80337152×1010（RLS）10] （公式1）Y=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] - L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] - L23÷[1.8802409472×1012（RLS）11] （公式2）公式中L为计算点至ZH“或HZ“的弧长HZ“：AK0+368.213的坐标从YH1：AK0+223.715推算，L=LS=HZ“-YH1=368.213-223.715=144.498将L=LS 代入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2+Y2）=131.5301偏角a1=arctg（Y÷X）=27°05’00.2”* 偏角计算用反正切公式，不要用其它公式。

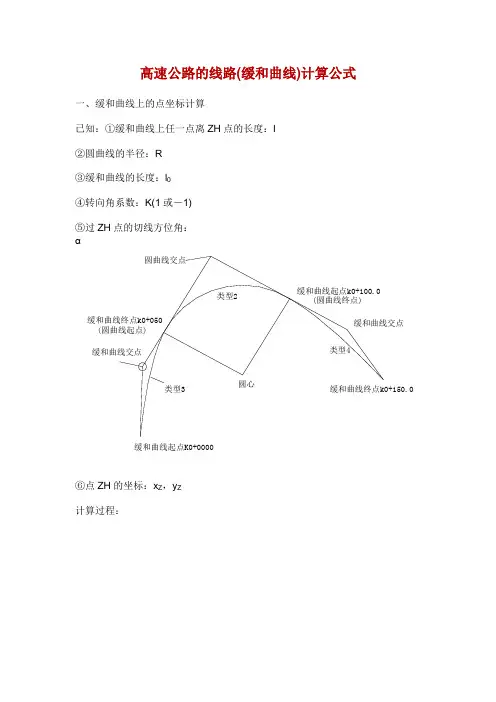
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y ②待求点的切线方位角：αT计算过程：。

高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R 2——曲线终点处的半径P——曲线起点处的曲率1——曲线终点处的曲率P2α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i(上坡为“＋”，下坡为“－”)1(上坡为“＋”，下坡为“－”)②第二坡度：i2③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K③曲线终点桩号：K1④曲线起点坐标：x0，y⑤曲线起点切线方位角：α⑥曲线起点处曲率：P(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式★★高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离点的长度：②圆曲线的半径：③缓和曲线的长度：④转向角系数：(或－)⑤过点的切线方位角：α⑥点的坐标：，计算过程：说明：当曲线为左转向时，，为右转向时，，公式中的取值如下：当计算第二缓和曲线上的点坐标时，则：为到点的长度α为过点的切线方位角再加上°值与计算第一缓和曲线时相反，为点的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离点的长度：②圆曲线的半径：③缓和曲线的长度：④转向角系数：(或－)⑤过点的切线方位角：α⑥点的坐标：，计算过程：说明：当曲线为左转向时，，为右转向时，，公式中的取值如下：当只知道点的坐标时，则：为到点的长度α为过点的切线方位角再加上°值与知道点坐标时相反，为点的坐标三、曲线要素计算公式公式中各符号说明：——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）——第一缓和曲线长度——第二缓和曲线长度——对应的缓和曲线长度——圆曲线半径——曲线起点处的半径——曲线终点处的半径——曲线起点处的曲率——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：(上坡为“＋”，下坡为“－”)②第二坡度：(上坡为“＋”，下坡为“－”)③变坡点桩号：④变坡点高程：⑤竖曲线的切线长度：⑥待求点桩号：计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：第二横坡：过渡段长度：待求处离第二横坡点（过渡段终点）的距离：求：待求处的横坡：解：()()六、匝道坐标计算已知：①待求点桩号：②曲线起点桩号：③曲线终点桩号：④曲线起点坐标：，⑤曲线起点切线方位角：α⑥曲线起点处曲率：(左转为“－”，右转为“＋”)⑦曲线终点处曲率：(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：②待求点的切线方位角：α计算过程：注：()函数是取符号函数，当<时()，当>时()，当时()。

公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间，由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。

1．缓和曲线的作用1）便于驾驶员操纵方向盘2）乘客的舒适与稳定，减小离心力变化3）满足超高、加宽缓和段的过渡，利于平稳行车4）与圆曲线配合得当，增加线形美观2．缓和曲线的性质为简便可作两个假定：一是汽车作匀速行驶；二是驾驶员操作方向盘作匀角速转动，即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。

S=A2/ρ（A：与汽车有关的参数）ρ=C/sC=A2由上式可以看出，汽车行驶轨迹半径随其行驶距离递减，即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比，此方程即回旋线方程。

3．回旋线基本方程即用回旋线作为缓和曲线的数学模型。

令：ρ=R，l h=s 则 l h=A2/R4．缓和曲线最小长度缓和曲线越长，其缓和效果就越好；但太长的缓和曲线也是没有必要的，因此这会给测设和施工带来不便。

缓和曲线的最小长度应按发挥其作用的要求来确定：1）根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性，就需控制离心力的变化率。

a1=0,a2=v2/ρ,a s=Δa/t≤0.62）依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3）根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡（即超高渐变率）是指在缓和曲线上设置超高缓和段后，因路基外侧由双向横坡逐渐变成单向超高横坡，所产生的附加纵坡。

4）从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间，视觉效果好。

《公路工程技术标准》规定：按行车速度来求缓和曲线最小长度，同时考虑行车时间和附加纵坡的要求。

5．直角坐标及要素计算1）回旋线切线角（1）缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。

缓和曲线逐桩坐标计算（转载）摘要：利用一缓和曲线算例，通过数学分析，推导出缓和曲线逐桩坐标计算公式，此公式可作为道路测设中的范例来运用，有很强的指导意义。

关键词：缓和曲线、公式、逐桩坐标一、引言道路建设中，由于受地形或地质影响，经常需要改变线路方向，为满足行车要求，往往要用曲线把两条直线连接起来。

曲线的构成形式无外乎圆曲线和缓和曲线，本文以河北省沿海高速某曲线段为例推导出缓和曲线的逐桩坐标计算公式，以方便图纸的审核，满足施工放样的需求。

本公式具有良好的操作性，方便施工、提高精度，可作为道路测设中的范例运用。

二、公式推导1 、实例数据河北省沿海高速公路一缓和曲线（如图）：AB 段为缓和曲线段，A 为ZH 点，B 为HY 点，R B=800m ；A 点里程为NK0+080 ，切线方位角为θA=100 ° 00 ′ 24.1 ″，坐标为X A=4355189.493,Y A=476976.267 ；B 点里程为NK0+158.125 ，切线方位角为θB=102 ° 48 ′ 15.6 ″，坐标为X B=4355174.669 ，Y B=477052.964 ，推求此曲线段内任意点坐标。

2 、公式推导及实例计算方法一：弦线偏角法1 ）公式推导由坐标增量的计算方法我们不难理解，求一点坐标可以根据其所在直线的方位角以及直线上另一点的坐标和距待求点的距离。

所以我们可以利用ZH 点，只要知道待求点距ZH 点的距离（弦长S ）和此弦与ZH 点切线方位角的夹角（转角a ），即可求出该点坐标。

根据回旋线方程C=RL ，用B 点数据推导出回旋线参数：C=RL S=800*78.125=62500 （L S为B 点至ZH 点的距离）设待求点距ZH 点距离为L因回旋线上任意点的偏角β0=L2/2RL S, 且转角a=β0/3 ，可得该点转角a 。

（曲线左转时a 代负值）。

根据缓和曲线上的弧弦关系S=L-L5/90R2L S2，可以求出待求点至ZH 点的弦长。

缓和曲线的坐标公式及推导第一章缓和曲线的坐标公式如图1-1所示,其坐标系是以缓和曲线起点ZH 为原点O，以切线为x轴，以过原点的曲线半径为y轴。

若原点O至P点的缓和曲线长度为，过P点切线与x轴的交角为β（即半径由∞变至的中心角）。

若P有微小变化至P′时，则增长，（x,y）增长（）,则有以下关系，图 1-1得，（2-1）由公式(常数)得知，故有则将上式代入（1-1）式中，得（2-3）上式即为缓和曲线上任一点直角坐标（x,y）的计算公式。

缓和曲线上任一点P的切线与x轴的交角，称为缓和曲线螺旋角，或称缓和曲线角。

其计算可由前面公式得（弧度）（2-4）若将代入（2-4）及（2-3）式中，则有以下结果：（2-5）上式即为缓和曲线终点HZ（ZH）的坐标及螺旋角的计算公式。

第二章圆曲线要素及计算公式如图2-1所示，两相邻直线偏角（线路转向角）为，选定其图 2-1连接曲线圆曲线的半径为R，这样，圆曲线和两直线段的切点位置ZY点、YZ点便被确定下来，我们称为对圆曲线相对位置起控制作用的直圆点ZY、圆直点YZ 和曲中点QZ为圆曲线三主要点。

我们称R、α以及具体体现三主要点几何位置的切线长T、曲线长L、外矢距E和切曲差（切线长和曲线长之差）D为曲线6要素。

只要知道了曲线6要素，便可于实地测放出圆曲线。

现将圆曲线的元素列下：：转向角（实地测出）R：曲率半径（设计给出）T：切线长（计算得出）L：曲线长（计算得出）D：切曲差（计算得出）偏角是在线路祥测时测放出的，圆曲线半径R是在设计中根据线路的等级以及现场地形条件等因素选定的，其余要素可根据以下公式计算：第三章偏角法测设介绍偏角法是一种极坐标标定点位的方法，它是用偏角和弦长来测设圆曲线细部。

如图3-1所示，1，2…，，…，n为设计之详测点，邻点间距均为c，弦长c所对应的圆心角为。

当放样至详测点时，可在ZY点置镜，后视JD方向，拨出偏角,再自-1点量距C和拨出的视线方向交会，即得出点。