综合曲线坐标计算

测量常用坐标计算公式(2010-07-01 22:13:21)标签：杂谈坐标计算公式坐标计算公式F1圆曲线-X=A+sin[90×(E-F)÷R÷π]cos[M+90×（E-F）÷R÷π] ×2×R Y=B+sin[90×(E-F)÷R÷π]sin [M+90×（E-F）÷R÷π] ×2×R K=M+180×（E-F）÷R÷πA:点为X轴坐标R为半径M为起点方位角E为起点里程F为计算点里程B为起点坐标Y为起点坐标K为计算点方位角F2直线+A=X+cosK×DX为起点坐标K为方位角B=Y+cosK×DY为起点坐标D为距离F3导线点F4缓和曲线+V=L 3÷6÷R÷LSV 为Y轴值R为半径 50为缓和曲线全长W=L-L 5÷40÷R 2÷LS2W为X轴值 L为弧长POI（V，W）M=tan -1（v÷w）M为计算方位角D=（W 2 +V 2）D为计算长度X=A+cos（J+M）×DX为X轴坐标J为该点方位角Y=B+sin（J+M）×DY为Y轴坐标K=J+28.6479×L 2÷R÷50K为切线方位角G=X+cos（K+J）×OG为平移后的坐标 O为平移的距离 I为转角角度H=Y+sin（K+J）×OH为转角后的坐标F5缓和曲线+V=L 3÷6÷R÷LSV为Y轴值R为半径 50为缓和曲线全长W=L-L 5÷40÷R 2÷LS 2W为X轴值 L为弧长M=tan -1（v÷w）M为计算方位角D=（W 2 +V 2）D为计算长度X=A+cos（J+M）×DX为X轴坐标J为该点方位角Y=B+sin（J+M）×DY为Y轴坐标K=J+28.6479×L 2÷R÷50K为切线方位角G=X+cos（K+J）×OG为平移后的坐标 O为平移的距离 I为转角角度H=Y+sin（K+J）×OH为转角后的坐标注：逆为负，顺为正。

曲线坐标计算通用公式（复化Simpson 公式）推导一、已知条件1、线元起点坐标：(),A A A x y2、线元起点切线方位角：A α3、线元起点里程：A K4、线元终点里程：B K 5、线元起点曲率半径：A ρ 6、线元终点曲率半径：B ρ二、求解问题求线元上任意点的坐标：(),C x y 。

即推导曲线坐标计算通用公式。

三、图示：如右上图（图中未示y ∆值） 四、坐标计算公式线元上任意点C 的坐标计算公式为：A x x x =+∆————① A y y y =+∆————②由上式可知，关键问题是求出x ∆、y ∆。

五、x ∆计算若AC 是直线，直接采用公式cos x l α∆=可求出x ∆（其中l 为A 、C 两点间直线距离，α为AC 直线方位角），但是，A 、C 两点间是任意曲线相连,不能直接用上述公式计算x ∆,需利用微积分原理计算。

1、曲线AB 上任意一点的曲率ρ计算采用内插法得：()B AA AB Ak k k k ρρρρ-=+--————③其中：k ——曲线AB 上任意一点的里程。

2、曲线AB 上任意一点的切线方位角α计算如右图：C 是曲线AB 上任意一点，AT 、TC 是A 、C 两点的切线，利用圆曲线求弧长公式得：()90A A k k A R π-=()90A k k Rδβπ-==其中：k ——曲线上任意点里程。

R ——曲线上任意点的曲率半径。

（通过公式③求得，1R ρ=）()()1190A A A R R k k ααπ=++-()()90A A A k k αρρπ=++-————④ 使用公式③、④时的符号规定：线元右偏：A ρ、B ρ均为“+”（即线元起终点曲率半径输正值）。

线元左偏：A ρ、B ρ均为“—”（即线元起终点曲率半径输负值）。

3、x ∆计算根据公式③、④可推知，()cos y k α=⎡⎤⎣⎦是里程间隔[],A C k k 上k 的一个连续函数，计算A 、C 两点的坐标增量x ∆，也就是求在里程段[],A C k k 内，x 坐标的改变量。

C A SI O f x-5800P综合曲线坐标计算程序说明：该程序适用于计算器C ASI O f x-5800P，可计算线路中心的缓和曲线、圆曲线、直线段，中、边桩坐标及切线方位角。

1、α? 输入转角：左转为负，右转为正2、R?输入圆曲线半径3、LS? 输入缓和曲线长度4、J D(DK)?输入交点里程桩号5、X(JD)?输入本交点X 坐标6、Y(JD)?输入本交点Y 坐标7、F W J?输入待求点切线方位角9、J? 输入0 程序计算中桩，输入 1 程序计算边桩10、JSDK? 输入里程桩号主程序名：ZHQ X1. Deg：Fix 4↙2. Lb1 A↙3. ＂α＂?A：?R：＂LS＂?C：＂JD(DK)＂?D：＂X(JD)＂?N：＂Y(JD)＂?E：＂FWJ＂?F↙4. Lb1 B↙5. ?J ↙6. C∧2÷24÷R-C∧（4）÷2688÷R∧（3）→P↙7. C÷2-C∧（3）÷240÷R∧2→Q↙8. 90×C÷兀÷R→B↙9. ＂T=＂：(R+P)tan(Abs(A)÷2)+Q→T◢10. ＂E=＂：(R+P)÷c o s(A÷2)-R→W◢11. ＂L=＂：(Abs(A)-2×B)兀R÷180+2×C→L◢12. ＂ZH=＂：D-T→G◢13. ＂HY=＂：G+C→H◢14. ＂QZ=＂：G+L÷2→I◢15. ＂YH=＂：G+L-C→K◢16. ＂HZ=＂：G+L→M◢17. If A＜0：Th en-1→S：E l se1→S：If End↙（本行中0 为数字）18. F+A÷2+90×S→U↙19. W+R→V↙20. N+V×cos(U)→B↙21. E+V×sin(U)→O↙（本行中O 为字母）22. Lbl 1 ↙23. ＂JS DK＂?Z↙24. If Z≤G：Th en T+G-Z→L ↙25. F+180→V ↙26. ＂FW J=＂：F→U◢27. Goto 2 ↙28. IfEnd ↙29. If Z≤H：Th en Z-G→L ↙30. L-L∧(5)÷(90×R∧2×C∧2)→V↙31. 30×L∧2×S÷(兀RC)→L ↙32. F+180→P ↙33. F+L→Q↙34. ＂FW J=＂：F+3×L→U◢35. Goto 4 ↙36. IfEnd ↙37. If Z≤K：Th en F+A÷2+90×S+180+180(Z-I)×S÷R÷兀→L↙38. ＂FW J=＂：L+90×S→U：If U≥360：The n U-360→U◢39. Else U→U◢40. IfEnd：G o to5：If End↙41. If Z≤M：Th en M-Z→L↙42. L-L∧(5)÷(90×R∧2×C∧2)→V↙43. 30×S×L∧2÷(兀RC)→L ↙44. F+A→P ↙45. F+A+180-L→Q↙46. ＂FW J=＂：F-3×L+A→U：If U≥360：Th en U-360→U◢47. Else U→U◢48. IfEnd：G o to4：If End↙49. If Z>M：Then Z-M+T→L↙50. F+A→U ↙51. U→V ↙52.G o to2 ↙53. Lbl 2 ↙54. ＂X=＂：N+L×cos(V)→X◢55. ＂Y=＂：E+L×sin(V)→Y◢56. G o to6 ↙57. If End↙58. Lbl 3 ↙59. ?W60. ＂XL=＂：X+W×cos(U-90)→P◢61. ＂YL=＂：Y+W×sin(U-90)→Q◢62. ＂XR=＂：X+W×cos(U+90)→P◢63. ＂XL=＂：Y+W×sin(U+90)→Q◢64. G o to1 ↙65. Lbl 4 ↙66. ＂X=＂：N+T×cos(P)+V×cos(Q)→X◢67. ＂Y=＂：E+T×sin(P)+V×cos(Q)→Y◢68. G o to6 ↙69.Lbl 5 ↙70. ＂X=＂：B+R×cos(L)→X◢71. ＂Y=＂：O+R×sin(L)→Y◢（本行中O 为字母）72. G o to6 ↙73. Lbl 6 ↙74. J=1 G o to3 ↙75. G o to1 ↙。

一、公路平曲线坐标计算公式1、缓和曲线：Lb1 0{K,D}①T=A2/R ②L=J（K-O）+T ③B=T2 /2/A2 *180/π④M=（L-T）-（L5-T5）/40/A4+（L9-T9）/3456/A8-（L13-T13）/599040/A12+（L17-T17）/17542600/A165.N=(L3-T3)/6/A2-(L7-T7)/336/A6+(L11-T11)/42240/A10-(L15-T15) /9676800/A14+(L19-T19)/3530097000/A18⑥I=(L2-T2)*180/2/A2/π⑦X=C+Mcos(Q-ZB)-ZNsin(Q-ZB)+Dcon(Q+ZI+S)◢⑧Y=F+Msin(Q-ZB)+ZNcos(Q-ZB)+Dsin(Q+ZI+S)◢Goto 0注：A：缘和曲线参数 R：起点半径 J：曲率半径判定值（当曲率半径由小到大取1,否则取-1）（当起点半径到终点半径是由大或无穷大到小取+1，反之则取-1） K：欲求点里程 O：缘和曲线起点里程 C：缘和曲线起点X坐标Q：起始方位角（当J=-1时，方位角应+180。

） Z：偏角判定值(当J=1时，左偏为-1，右偏为1；当J=-1时，左偏为1，右偏为-1) D：距中桩的距离 S：斜交角度 F：缘和曲线起点Y坐标2、圆曲线Lb1 0{K,D}①L=K-0②X=C+R[sin(Q+L/R*180/π)-sinQ]+Dcos(Q+L/R*180/π+S)◢③Y=F-R[cos(Q+L/R*180/π)-cosQ]+Dsin(Q+L/R*180/π+S)◢ Goto 0注：K：欲求点里程 O：圆曲线起点里程 C：圆曲线起点X坐标 R：圆曲线半径 (左偏为负) Q：起始方位角 D：距中桩的距离 S：斜交角度 F：圆曲线起点Y坐标3、直线Lb1 0{K,D}①L=K-0②X=C+LcosQ+Dcos(Q+S)◢③Y=F+LsinQ+Dsin(Q+S)◢Goto 0注：K：欲求点里程 O：直线起点里程 C：直线起点X坐标 Q：起始方位角 D：距中桩的距离 S：斜交角度 F：直线起点Y坐标二、竖曲线计算公式Lb1 0①{K} ②L=K-（0-T）③H=M-IT+LI-ZL2 /2/R◢ Goto 0 注：K：欲求点里程;O：顶点里程;T：切线长;M：顶点高程;I：坡度;Z：竖曲线判定值三、预拱度计算公式Lb1 0①{K} ②H=D-(4D÷B2)×(B/2-(K-O)) 2◢ Goto 0注：D：跨中最大设计预拱度 H：要计算的预拱度 K：欲求点里程桩号（距支座的距离） O：起点桩号 B：本跨净长。

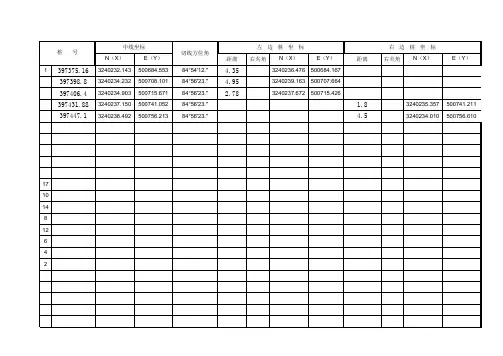
圆曲线坐标计算交点桩号YK20+734.498；N=2889769.961；E=527002.305 ；方位角314'24'58.3' 转角27'19'31.4' 切线长度T1= 814.345 ；T2= 814.347 ；半径R=3000 ；曲线长度LS1：170；LC=1260.752；LS2= 170 曲线总长=1600.752 求ZH,HY,QZ,YH,HZ以及圆心点的坐标。

1、A？输入转(偏)角；左转为负，右转为正。

转角27'19'31.4'2、R？输入曲线半径。

30003、LS？输入缓和曲线长度。

1704、JD（DK）？输入交点里程桩号。

20734.498结果显示T = 814.347 W=87.776 L=1600.754 ZH=19920.151;HY=20090.151; QZ=20720.528; YH=21350.905; HZ=21520.9055、X（JD）？输入本交点X坐标。

2889769.9616、Y（JD）？输入本交点Y坐标。

527002.3057、FWJ？输入直缓(ZH)点切线方位角。

314'24'58.3'8、J？输入0程序计算中桩，输入1程序计算边桩。

09、Z？输入里程桩号。

ZH=19920.151FWJ:314.416 X=2889200.028 Y= 527583.973完（FWJ:314.416=314'24'57.6' ）ZH(2889200.026 527583.975) HY(2889320.140 527463. 682)QZ(2889816.373 527076.808) YH(2890382.383 526801.950)HZ(2890543.311 526747.167)例如2:JD15:4013872.8781;456031.1661 JD16:4015349.321;451808.075ZH:75+137.901 ay:16.45.49.69 R=9000 缓和曲线长：490 T=1571.257 JD(DK) =76709.158 FWJ=289-16-12.85 给我算一下74+400;75+300;75+800;76+500左中线坐标。

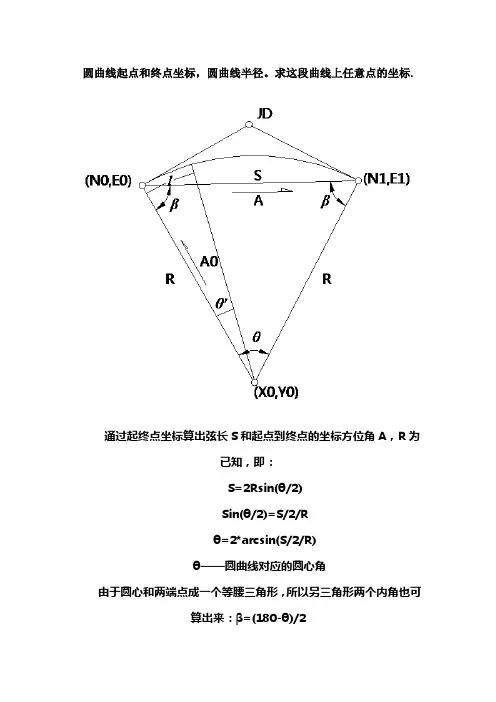
圆曲线起点和终点坐标，圆曲线半径。

求这段曲线上任意点的坐标.通过起终点坐标算出弦长S和起点到终点的坐标方位角A，R为已知，即：S=2Rsin(θ/2)Sin(θ/2)=S/2/Rθ=2*arcsin(S/2/R)θ——圆曲线对应的圆心角由于圆心和两端点成一个等腰三角形，所以另三角形两个内角也可算出来：β=(180-θ)/2由坐标正算公式可算得圆心坐标,和圆心到起点的坐标方位角，即：X0=N0+Rcos(A+β)Y0=E0+Rsin(A+β)A0= A+β+180根据弧长公式l=R*θ（θ——长度为l的弧长所对应的圆心角，以弧度为单位）可以算得该圆曲线上距起点任意弧长所对应的圆心角偏转值：θ’=180*l/π/R故圆曲线上任意一点的坐标即可再次使用坐标正算公式得出：X=X0+Rcos(A0+θ’)Y=Y0+Rsin(A0+θ’)以上算例只需用到坐标正反算知识，其他知识都是基于初中几何水平的解算，所以只要多动一下脑子，办法是很多的，读者也可以算出JD 坐标和前直线方位角用手头上已有的程序解算。

一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值。

卵形曲线是高等级公路、立交桥匝道常见的曲线形式，它由基本的三部分构成：第一圆曲线段、缓和曲线段和第二圆曲线段。

中间段缓和曲线用来连接两个不同半径的圆曲线。

其中线坐标解算方法有如下几种：1 补全缓和曲线我国公路上采用的缓和曲线为辐射螺旋线，夹在两圆曲线中间的缓和曲线为整个缓和曲线的一部分，缓和曲线上任一点半径与该点至该缓和曲线起点的距离乘积为一定值：R×L ＝ A ，假设 R1＞ R2，可由两圆半径及两圆间的缓和段长 ls，求缓和曲线的总长 L 。

Δl ＝ L － l s (1)Δl 就是夹在两圆曲线间缓和段省去的部分，由 YH 点补长Δl 至 o 点，以 o 点为该缓和曲线起点，起点的切线方向为 x 轴，与之垂直的曲线内侧方向为 y轴方向建立坐标系（图 1 ）。

缓和曲线公式（推导过程略）如下：(2)(3)图 1利用 x 、 y 值可以求得 o—YH 弦与 x 轴的夹角：β＝ 3δ。

α1为YH 点的切线方位角，则 ox 的方位：α＝α1±β。

o 点的坐标可由几何关系求得为（ x0， y）。

缓和段上任一点统一坐标可求得：(4)y=yo+xsinα±ycosα (5) 2 曲率推算缓和曲线段曲率半径由第一段圆曲线半径 R1变为第二段曲率半径 R2（假设 R1＞ R2），则缓和曲线曲率半径变化为： (6)其中 ls为中间段缓和曲线长，为求缓和曲线方程，现建立以缓和曲线起点为坐标原点，起点的切线方向为 x 轴，与之垂直的曲线内侧方向为 y 轴的坐标系（图2 ），设 P 点为缓和曲线上任一点，距原点的曲线长为 l ，该点附近的微分弧长为 dl ，缓和曲线偏角为β，则有dx=dlcosβ (7)dy=dlsinβ (8)图 2由于将其代入上式并进行积分可得缓和曲线方程：(9)(10)中间缓和段统一坐标计算为：(11)Y ＝ yYHxsinα±ycosα (12)α为曲线 YH 点切线方位。

一、圆曲线坐标计算公式β=180°/π×L/R（L= βπR/180°）弧长公式β为圆心角△X=sinβ×R△Y=(1-cosβ) ×RC= 弦长X=X1+cos (α±β/2)×CY=Y1+sin (α±β/2)×Cβ代表偏角,（既弧上任一点所对的圆心角）。

β/2是所谓的偏角（弦长与切线的夹角）△X 、△Y 代表增量值。

X 、Y 代表准备求的坐标。

X1、Y1代表起算点坐标值。

α代表起算点的方位角。

R 代表曲线半径二、缓和曲线坐标计算公式β= L2/2RLS ×180°/πC= L - L5/90R2L S 2X=X1+cos (α±β/3)×CY=Y1+sin (α±β/3)×C L 代表起算点到准备算的距离。

LS 代表缓和曲线总长。

X1、Y1代表起算点坐标值。

三、直线坐标计算公式X=X1+cosα×LY=Y1+sinα×LX1、Y1代表起算点坐标值α代表直线段方位角。

L 代表起算点到准备算的距离。

1）左右边桩计算方法X 边=X中+cos（α±90°) ×LY 边=Y中+sin（α±90°) ×L在计算左右边桩时，先求出中桩坐标，在用此公式求左右边桩。

如果在线路方向左侧用中桩方位角减去90°，线路右侧加90°，乘以准备算的左右宽度。

例题:直线坐标计算方法α(方位角)=18°21′47″DK184+714.029，求DK186+421.02里程坐标X1=84817.831 Y1=352.177 起始里程解:根据公式X=X1+cosα×LX=84817.831+COS18°21′47″×(86421.02—84714.029)=86437.901Y=Y1+sinα×LY=352.177+sin18°21′47″×(86421.02—84714.029)=889.943求DK186+421.02里程左右边桩, 左侧3.75m, 右侧7.05m. 解:根据公式线路左侧计算:X 边=X中+cos（α±90°) ×LX 边=86437.901+cos(18°21′47″- 90°) ×3.75=86439.082Y 边=Y中+sin（α±90°) ×LY 边=889.943+sin(18°21′47″- 90°) ×3.75=886.384线路右侧计算:X 边=X中+cos（α±90°) ×LX 边=86437.901+cos(18°21′47″+ 90°) ×7.05=86435.680Y 边=Y中+sin（α±90°) ×LY 边=889.943+sin(18°21′47″+90°) ×7.05=896.634四、例题:缓和曲线坐标计算方法α(ZH点起始方位角)=18°21′47″X1=86437.901 Y1=889.941 起始里程DK186+421.02曲线半径2500 缓和曲线长120m求HY 点坐标, 也可以求ZH 点到HY 点任意坐标解:根据公式β=L2/2RLS×180°/πβ=｛1202/(2×2500×120) ｝×(180°/π)= 1°22′30.36″C=L-L5/90R2LS2C=120-1205/(90×25002×1202)=119.997X=X1+cos(α±β/3)×CX=86437.901+cos(18°21′47″-1°22′30.36″/3)×119.997=86552.086Y=Y1+sin(α±β/3)×CY=889.941+sin(18°21′47″-1°22′30.36″/3)×119.997=926.832求DK186+541.02里程左右边桩, 左侧3.75m, 右侧7.05m. 解:根据公式线路左侧计算:X 边=X中+cos（α±90°) ×LX 边=86552.086+cos｛(18°21′47″-1°22′30.36″)- 90°｝×3.75=86553.182Y 边=Y中+sin（α±90°) ×LY 边=926.832+sin｛(18°21′47″-1°22′30.36″)- 90°｝×3.75=923.246线路右侧计算:X 边=X中+cos（α±90°) ×LX 边=86552.086+cos｛(18°21′47″-1°22′30.36″)+ 90°｝×7.05=86550.026Y 边=Y中+sin（α±90°) ×LY 边=926.832+sin｛(18°21′47″-1°22′30.36″)+ 90°｝×7.05=933.574缓和曲线方位角计算方法α=(起始方位角±β偏角)= 18°21′47″-1°22′30.36″=16°59′16.64″注:缓和曲线在计算坐标时, 此公式只能从两头往中间推, 只能从ZH 点往HY 点推,HZ 点往YH点推算, 如果YH 往HZ 点推算坐标, 公式里的β为β2/3.五、例题:圆曲线坐标计算方法α(HY点起始方位角)= 16°59′16.64″X1=86552.086 Y1=926.832曲线半径2500 曲线长748.75 起始里程DK186+541.02求YH 点坐标, 也可以求QZ 点坐标或任意圆曲线一点坐标. 解:根据公式β=180°/π×L/Rβ= 180°/π×748.75/2500=17°09′36.31″△X=sinβ×R△X=sin17°09′36.31″×2500=737.606△Y=(1-cosβ) ×R△Y=(1-cos17°09′36.31″) ×2500=111.290C= 弦长C=745.954X=X1+cos(α±β/2)×CX= 86552.086 +cos(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=87290.023 Y=Y1+sin(α±β/2)×CY=926.832+ sin(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=1035.905圆曲线方位角计算方法α=(起始方位角±β偏角)= 16°59′16.64″+360°-17°09′36.31″=359°49′40.33″求DK187+289.77里程左右边桩, 左侧3.75m, 右侧7.05m. 解:根据公式线路左侧计算:X 边=X中+cos（α±90°) ×LX 边=87290.023+cos(359°49′40.33″-90°) ×3.75=87290.012 Y 边=Y中+sin（α±90°) ×LY 边=1035.905+sin(359°49′40.33″-90°) ×3.75=1032.155线路右侧计算:X 边=X中+cos（α±90°) ×LX 边=87290.023+cos(359°49′40.33″+90°) ×7.05=87290.044 Y 边=Y中+sin（α±90°) ×LY 边=1035.905+sin(359°49′40.33″+90°) ×7.05=1042.955。

圆曲线坐标计算公式β=180°/π×L/R （L= βπ R/180°）弧长公式β为圆心角△X=sinβ×R△Y=(1-cosβ)×RC= 2Rsin(（90度乘以L）除以（π乘以R）)X=X1+cos (α ±β/2)×CY=Y1+sin (α ±β/2)×Cβ代表偏角,（既弧上任一点所对的圆心角）。

β/2是所谓的偏角（弦长与切线的夹角）△X、△Y代表增量值。

X、Y代表准备求的坐标。

X1、Y1代表起算点坐标值。

α代表起算点的方位角。

R 代表曲线半径缓和曲线坐标计算公式β= L2/2RL S ×180°/πC= L - L5/90R2L S2X=X1+cos (α ±β/3)×CY=Y1+sin (α ±β/3)×CL代表起算点到准备算的距离。

LS代表缓和曲线总长。

X1、Y1代表起算点坐标值。

直线坐标计算公式X=X1+cosα×LY=Y1+sinα×LX1、Y1代表起算点坐标值α代表直线段方位角。

L代表起算点到准备算的距离。

左右边桩计算方法X边=X中+cos（α±90°)×LY边=Y中+sin（α±90°)×L在计算左右边桩时，先求出中桩坐标，在用此公式求左右边桩。

如果在线路方向左侧用中桩方位角减去90°，线路右侧加90°，乘以准备算的左右宽度。

例题:直线坐标计算方法α(方位角)=18°21′47″X1=84817.831 Y1=352.177 起始里程DK184+714.029求DK186+421.02里程坐标解:根据公式X=X1+cosα×LX=84817.831+COS18°21′47″×(86421.02—84714.029)=86437.901Y=Y1+sinα×LY=352.177+sin18°21′47″×(86421.02—84714.029)=889.943求DK186+421.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos（α±90°)×LX边=86437.901+cos(18°21′47″- 90°)×3.75=86439.082Y边=Y中+sin（α±90°)×LY边=889.943+sin(18°21′47″- 90°)×3.75=886.384线路右侧计算:X边=X中+cos（α±90°)×LX边=86437.901+cos(18°21′47″+ 90°)×7.05=86435.680Y边=Y中+sin（α±90°)×LY边=889.943+sin(18°21′47″+90°)×7.05=896.634例题:缓和曲线坐标计算方法α(ZH点起始方位角)=18°21′47″X1=86437.901 Y1=889.941 起始里程DK186+421.02曲线半径2500 缓和曲线长120m求HY点坐标,也可以求ZH点到HY点任意坐标解:根据公式β=L2/2RLS×180°/πβ=｛1202/(2×2500×120)｝×(180°/π)= 1°22′30.36″C=L-L5/90R2LS2C=120-1205/(90×25002×1202)=119.997X=X1+cos(α±β/3)×CX=86437.901+cos(18°21′47″-1°22′30.36″/3)×119.997=86552.086Y=Y1+sin(α±β/3)×CY=889.941+sin(18°21′47″-1°22′30.36″/3)×119.997=926.832求DK186+541.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos（α±90°)×LX边=86552.086+cos｛(18°21′47″-1°22′30.36″)- 90°｝×3.75=86553.182Y边=Y中+sin（α±90°)×LY边=926.832+sin｛(18°21′47″-1°22′30.36″)- 90°｝×3.75=923.246线路右侧计算:X边=X中+cos（α±90°)×LX边=86552.086+cos｛(18°21′47″-1°22′30.36″)+ 90°｝×7.05=86550.026Y边=Y中+sin（α±90°)×LY边=926.832+sin｛(18°21′47″-1°22′30.36″)+ 90°｝×7.05=933.574缓和曲线方位角计算方法α=(起始方位角±β偏角)= 18°21′47″-1°22′30.36″=16°59′16.64″注:缓和曲线在计算坐标时,此公式只能从两头往中间推,只能从ZH点往HY点推,HZ点往YH点推算,如果YH往HZ点推算坐标,公式里的β为β2/3.例题:圆曲线坐标计算方法α(HY点起始方位角)= 16°59′16.64″X1=86552.086 Y1=926.832曲线半径2500 曲线长748.75 起始里程DK186+541.02求YH点坐标,也可以求QZ点坐标或任意圆曲线一点坐标.解:根据公式β=180°/π×L/Rβ= 180°/π×748.75/2500=17°09′36.31″△X=sinβ×R△X=sin17°09′36.31″×2500=737.606△Y=(1-cosβ)×R△Y=(1-cos17°09′36.31″)×2500=111.290C= 弦长C=745.954X=X1+cos(α±β/2)×CX= 86552.086 +cos(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=87290.023Y=Y1+sin(α±β/2)×CY=926.832+ sin(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=1035.905圆曲线方位角计算方法α=(起始方位角±β偏角)= 16°59′16.64″+360°-17°09′36.31″=359°49′40.33″求DK187+289.77里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos（α±90°)×LX边=87290.023+cos(359°49′40.33″-90°)×3.75=87290.012Y边=Y中+sin（α±90°)×LY边=1035.905+sin(359°49′40.33″-90°)×3.75=1032.155线路右侧计算:X边=X中+cos（α±90°)×LX边=87290.023+cos(359°49′40.33″+90°)×7.05=87290.044Y边=Y中+sin（α±90°)×LY边=1035.905+sin(359°49′40.33″+90°)×7.05=1042.955。

一、圆曲线范围公式
已知：半径R.转向角β
1、切线长T=Rtan(β/2)
2、曲线长L=（Rπβ）/180
3、外矢距E=R(1/cos(β/2)-1)
4、切曲差q=2T-L
偏角公式δ=180C/2Rπ注C为所点弧长
二、缓和曲线范围公式
1、缓和曲线切线角βn=90Ln2/RπLs Ln为所点n到直缓或缓直点曲线长Ls---缓和曲线长
2、缓和曲线偏角公式：
δn=30 Ln2/RπLs
3、切线长T=m+(R+P)tan(β/2)
4、曲线长：
L=（Rπ(β-2β0）)/180+2Ls
5、外矢距E=(R+P)/cos(β/2)-R
6、切曲差q=2T-L
7、切垂距m=Ls/2-Ls3/240R2
8、内移距P=Ls2/24R- Ls4/2688R3
9、缓和曲线数学坐标公式：
X=Ls-Ln5/40R2Ls2
Y= Ln3/6RLs- Ln7/336 R3Ls3
10、缓和曲线偏角公式：
δn=tan-1(y/x)
11、缓和曲线弦长公式:Ci=√(x2+y2) Cc=Ln-Ln3/90R2+Ln5/3888 R4(代数式综合曲线中圆曲线范围坐标公式：Xi=m+Li-Ls/2-(Li-Ls/2)3/6R2
Yi=p+(Li- Ls/2)2/2R-(Li- Ls/2)4/24R3注：Li为圆曲线上任意点到ZH或
HZ的曲线长（用于计算偏移值）三、竖曲线计算公式
Y=X2/2R。

曲线道路坐标计算(Excel)曲线道路坐标计算§1 曲线要素计算缓和曲线是在不改变直线段方向和保持圆曲线半径不变的条件下，插入到直线段和圆曲线之间的。

其曲率半径ρ从直线的曲率半径∞（无穷大）1逐渐变化到圆曲线的半径R，在缓和曲线上任意一点的曲率半径ρ与缓和曲线的长度l成反比，以公式表示为：ρ∝ 或ρ⋅l=C（C为常数，称l曲线半径变更率）。

当l=lo时，ρ=R，应有C=ρ⋅l=R⋅lo以上几式是缓和曲线必要的前提条件。

在实际应用中，可采取符合这一前提条件的曲线作为缓和曲线。

常用的有辐射螺旋线及三次抛物线，我国采用辐射螺旋线。

为了在圆曲线与直线之间加入一段缓和曲线lo，原来的圆曲线需要在垂直于其切线的方向移动一段距离p，因而圆心就由O'移到O，而原来的半径R保持不变，如图。

由图中可看出，缓和曲线约有一半的长度是靠近原来的直线部分，而另一半是靠近原来的圆曲线部分，原来圆曲线的两端其圆心角βo相对应的那部分圆弧，现在由缓和曲线所代替，因而圆曲线只剩下缓圆点(HY)到圆缓点(YH)这段长度即ly。

βo为缓和曲线的切线角，即缓圆点或圆缓点切线与直缓点或缓直点切线的交角，亦即圆曲线HY→YH两端各延长γ为缓和曲线总偏角，即从直缓点(ZH)测设缓圆点(HY)或从缓直点(HZ)测设圆缓点(YH)的偏角。

q为切线增量(切垂距)，即ZH(或HZ)到从圆心O向ZH(或HZ)的切线作垂线垂足的距离。

p为圆曲线内移值，即垂线(从圆心O向ZH(或HZ)的切线作垂线)长与圆曲线半径R之差。

lo部分所对应的圆心角。

2§1.1 不等长缓和曲线要素计算：在铁路曲线测设中，线路曲线一般是由相等的两条缓和曲线中间加一个圆曲线构成，有时还会出现由两个不等长的缓和曲线中间加一个圆曲线构成的特殊情况，如图：缓和曲线长分别为lo1、lo2 ，切线长分别为T1、T2 ，曲线偏角(线路转角)为α，圆曲线半径为R，圆曲线长为ly ，曲线长为L ，外矢距为E ，切曲差为J，(缓和曲线后)圆曲线内移值分别为p1、p2，(缓和曲线)切线增量分别为q1、q2，缓和曲线偏角分别为βo1、2βo2 ，回旋线参数分别为A12=Rlo1、A2=Rlo2各曲线要素计算公式如下：llq1=o1-o122240R3T2=q2+(R+p2)tgα2+(p1-p2)sinαllq2=o2-o222240Rllp1=o1-o1324R2688Rllp2=o2-o2324R2688R2243βo1=lo118090lo1⋅= 2RππRβo2=lo218090lo2⋅= 2RππRL=lo1+lo2+(α-βo1-βo2)πR180︒T1=q1+(R+p1)tgα2+(p2-p1)sinα从以上公式可以看出，当lo1=lo2时，就是等长(对称)缓和曲线的情况。

一、曲线的一般组成 缓和曲线常数1、曲线内移距：R l P s 242=2、切垂距：23s s 2402m R l l -=3、缓和曲线基本角：RL Sπβ90=4、缓和曲线偏角：RL Sπδ30=5、缓和曲线反偏角：RL Sπ60b =缓和曲线综合要素 切线长()m P R T +•+=)2tan(α曲线长()S L R L22+-=βα曲外失距()R P R E -⎪⎭⎫⎝⎛+=2cos α 切曲差q=2T-曲L直线+缓和曲线+圆曲线+缓和曲线+直线。

从小里程至大里程依次为ZH （直缓点）、HY （缓圆点）、YH （圆缓点）、HZ （缓直点）如下图所示：二、方位角的概念从标准方向的正北端起,顺时针方向到直线的水平角称为该直线的方位角。

方位角的取值范围为0°～360°，如下图A即为直线L的方位角。

三、某点坐标的计算已知A 点坐标为（Xa ，Ya ），B 点距离A 点为L ，直线AB 的方位角为α，计算B 点坐标。

计算方法： X=Xa+L ×cos α Y=Ya+L ×sin α四、曲线上任一点的坐标及切线方位角计算 首先计算直线段坐标方位角（即ZH ～JD 坐标方位角），及ZH 点坐标。

1、计算缓和曲线上待求点偏角=sRL L π230。

其中L=待求点至ZH 距离、R=圆曲线半径、sL =缓和曲线长。

2、待求点方位角=直线方位角±待求点偏角。

（曲线左转-偏角，曲线右转+偏角）3、待求点至ZH点弦长=22590SL R L L -，其中L=待求点至ZH 距离（里程）、R=圆曲线半径。

4、待求点坐标：X=ZH 点X 坐标+COS （待求点方位角）*弦长 Y= ZH 点Y 坐标+SIN （待求点方位角）*弦长缓和曲线计算左右边线坐标(ZH～HY)1、左侧方位角=（待求点方位角±2倍偏角=直线方位角±3倍偏角）—边线与中线夹角。

2、右侧方位角=（待求点方位角±2倍偏角=直线方位角±3倍偏角）+边线与中线夹角。

[正确] CASIO fx-5800P综合曲线坐标计算程序说明：该程序适用于计算器CASIO fx-5800P，可计算线路中心的缓和曲线、圆曲线、直线段，中、边桩坐标及切线方位角。

主程序：QXZB？LL=0=> Goto0L=1=> Goto1L=-1=> Goto2Lbl 0：？ZIf Z≤缓直：Then 转角→A：半径→R：缓和曲线长度→C：交点里程桩号→D：交点X 坐标→N：交点Y 坐标→E：方位角→F：Prog＂ZHQX＂：Goto0：IfEnd输入下一段交点，与上一致（主线要素）Lbl 1：？ZIf Z≤缓直：Then 转角→A：半径→R：缓和曲线长度→C：交点里程桩号→D：交点X 坐标→N：交点Y 坐标→E：方位角→F：Prog＂ZHQX＂：Goto1：IfEnd输入下一段交点，与上一致（分离式右线要素）Lbl 2：？ZIf Z≤缓直：Then 转角→A：半径→R：缓和曲线长度→C：交点里程桩号→D：交点X 坐标→N：交点Y 坐标→E：方位角→F：Prog＂ZHQX＂：Goto2：IfEnd输入下一段交点，与上一致（分离式左线要素）程序名：ZHQX10→DimZ↙C∧2÷24÷R-C∧（4）÷2688÷R∧（3）→P↙C÷2-C∧（3）÷240÷R∧2→Q↙90×C÷兀÷R→B↙(R+P)tan(Abs(A)÷2)+Q→T(R+P)÷cos(A÷2)-R→W(Abs(A)-2×B)兀R÷180+2×C→LD-T→GG+C→Z[1]G+L÷2→IG+L-C→Z[2]G+L→Z[3]?J↙If A＜0:Then -1→S:Else 1→S:IfEnd↙（……本行中0为数字）F+A÷2+90×S→U↙W+R→V↙N+V×cos(U)→B↙E+V×sin(U)→O↙（……本行中O 为字母）Lbl 1↙If Z≤G:Then T+G-Z→L↙F+180→V↙＂FWJ= ＂:F→U◢Goto 2↙IfEnd↙If Z≤Z[1]:Then Z-G→L↙L-L∧(5)÷(90×R∧2×C∧2)→V↙30×L∧2×S÷(兀RC)→L↙F+180→P↙F+L→Q↙＂FWJ= ＂:F+3×L→U◢Goto 4↙IfEnd↙If Z≤Z[2]:Then F+A÷2+90×S+180+180(Z-I)×S÷R÷兀→L↙＂FWJ= ＂:L+90×S→U◢Goto 5↙IfEnd↙If Z≤Z[3]:Then Z[3]-Z→L↙L-L∧(5)÷(90×R∧2×C∧2)→V↙30×S×L∧2÷(兀RC)→L↙F+A→P↙F+A+180-L→Q↙＂FWJ= ＂:F-3×L+A→U◢Goto 4↙IfEnd↙If Z> Z[3]:Then Z- Z[3]+T→L↙F+A→U↙U→V↙Goto 2↙Lbl 2↙＂X= ＂:N+L×cos(V)→X◢＂Y= ＂:E+L×sin(V)→Y◢Goto 6↙IfEnd↙Lbl 4↙＂X= ＂:N+T×cos(P)+V×cos(Q)→X◢＂Y= ＂:E+T×sin(P)+V×sin(Q)→Y◢Goto 6↙Lbl 5↙＂X= ＂:B+R×cos(L)→X◢＂Y= ＂:O+R×sin(L)→Y◢（……本行中O为字母）Goto 6↙Lbl 6↙J=1=> Prog＂BZ＂↙（……“=>”输入步：Function→下翻↓→下翻↓→3：=>）程序名：BZ＂BZK＂?H:＂L,R＂?K: ＂FWJ＂?M＂XZ=＂:X+HK cos(U+M)→P◢＂YZ=＂:Y+HK sin(U+M)→Q◢注：1、◢为输出指令。

四、圆曲线的详细测设（一）偏角法以曲线起点或终点至曲张上任一点p i的弦线与切线T之间的弦切角A 和弦长C,确定P i的位置。

—2 2RC =2只工丛（一）切线支距法以曲线的zy或yz点为原点，切线为x轴，过原点的半径为y轴，根据坐标x,y测设曲线上各桩点P i。

测设时分别从曲线的起点和终点向中点各测设曲线的一半，采用整桩距法设桩，即弧长I （20m，10m, 5m）。

设l i为所测点至原点间的弧长。

®i 为 l i 所对的圆心角。

y j =R(1-cos 半j)CP 丄180 iR JI施测步骤:1）从Zy点开始用钢尺沿切线方向量取P i的横坐标X i，得垂足N i。

2、全站仪极坐标法（在统一的测量坐标系中，任意已知控制点上设站,放任何曲线的点）关键计算点在测是坐标系中的坐标。

X i，Y i已知：交点JD2的偏角I =90 R=50m的里程k i +300 XJD2 = 5000m yJD^ 5000mJD1的方位角^12 =30 P点的里程k1+276.18m（一）求圆心0的坐标x0, y0180 —I畑“12 +1 +—2—180-9030+90 +------- =165= 2S(JD2 -0)=巳工丄=50/E聖=70.712 2x0 =XJD2 +S cosa20 =5000 +70.71cos165" = 4931.70my o = yJD2 +S 逞口20 =5000 + 70.71工 165 =5018.30m（二）求P点的坐标I =p的里程-zy里程=K1+ 276.18-(k1+300-50) = 26.18m-丄竺=迤沢竺=30R 兀50 兀50a op= a12+90+180+ 半=30° + 270。

+ 30。

= 330"xp = x0+Rcnxop = 4931.70+ 50X cn330° =4975.0m yp = yo + P = 5018.30 + 50% ©330” =4993.30m有缓和曲线的圆曲线计算公式(1) (3) 1、曲线的基本公式P = f 其中 c = RI s I s ――缓和曲线全长。