基于MATLAB生成模糊控制规则离线查询表

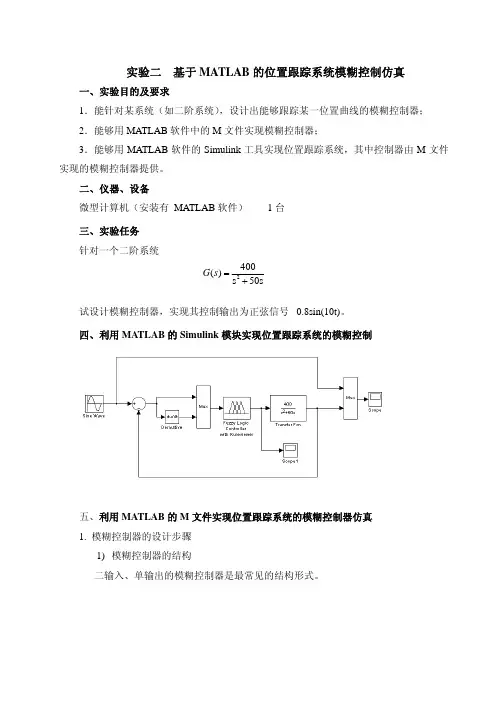
实验二 基于MATLAB 的位置跟踪系统模糊控制仿真一、实验目的及要求1．能针对某系统（如二阶系统），设计出能够跟踪某一位置曲线的模糊控制器； 2．能够用MATLAB 软件中的M 文件实现模糊控制器；3．能够用MATLAB 软件的Simulink 工具实现位置跟踪系统，其中控制器由M 文件实现的模糊控制器提供。

二、仪器、设备微型计算机（安装有 MATLAB 软件） 1台 三、实验任务 针对一个二阶系统 s50s 400)(2+=s G试设计模糊控制器，实现其控制输出为正弦信号0.8sin(10t)。

四、利用MATLAB 的Simulink 模块实现位置跟踪系统的模糊控制五、利用MATLAB 的M 文件实现位置跟踪系统的模糊控制器仿真 1. 模糊控制器的设计步骤1) 模糊控制器的结构二输入、单输出的模糊控制器是最常见的结构形式。

System fuzzf: 2 inputs, 1 outputs, 49 rulesec (7)图2-1 模糊控制器的结构示意图2) 定义输入输出模糊集对误差E 、误差变化EC 及控制量u 的模糊集及其论域定义如下：E 、EC 和u 的模糊集均为： {}PB PM PS Z NS NM NB ,,,,,,E 、EC 的论域均为：{-3，-2，-1，0，1，2，3} u 的论域为：{-4.5,-3,-1.5,0,1,3,4.5}3) 定义输入输出隶属函数模糊变量误差E 、误差变化EC 及控制量u 的模糊集和论域确定后，需对模糊语言变量确定隶属函数，确定论域内元素对模糊语言变量的隶属度。

4) 建立模糊控制规则根据人的经验，根据系统输出的误差及误差的变化趋势来设计模糊控制规则。

模糊控制规则语句构成了描述众多被控过程的模糊模型。

5) 建立模糊控制表模糊控制规则可采用模糊规则表2-1来描述，共49条模糊规则，各个模糊语句之间是或的关系，由第一条语句所确定的控制规则可以计算出u1。

如何利用Matlab进行模糊控制引言近年来，随着科技的不断发展，模糊控制作为一种重要的控制方法，在各个领域得到了广泛的应用。

而Matlab作为一款功能强大的数学工具软件，对于模糊控制的实现提供了便捷的支持。

本文将介绍如何利用Matlab进行模糊控制，以及其在实际应用中的优势和局限性。

一、模糊控制简介模糊控制是一种基于模糊逻辑的控制方法，它通过将模糊规则应用于控制系统，使其能够对不确定性和模糊信息进行处理。

与传统的精确控制方法相比，模糊控制更适用于处理复杂系统或无法精确建模的系统。

二、Matlab中的模糊控制工具箱Matlab提供了专门的模糊控制工具箱，可以方便地实现模糊控制系统的建模、仿真和优化等操作。

在Matlab的模糊控制工具箱中，主要包括两个核心部分：模糊推理引擎和模糊控制器。

1. 模糊推理引擎模糊推理引擎是模糊控制系统的核心部分，它负责根据输入和模糊规则，对系统进行推理和输出控制量。

在Matlab中，可以使用命令"newfis"来创建一个新的模糊控制系统，然后通过定义输入和输出变量、设定隶属函数和模糊规则等步骤，来构建一个完整的模糊控制系统。

2. 模糊控制器模糊控制器是模糊控制系统的具体实现，它将模糊推理引擎与输入输出之间的映射关系结合起来。

在Matlab中，可以使用命令"newfis"创建一个新的模糊控制系统，然后使用"addInput"和"addOutput"来添加输入和输出变量，最后通过设定隶属函数和模糊规则等步骤，来实现模糊控制器的搭建。

三、模糊控制的实际应用模糊控制在实际应用中有着广泛的应用领域，例如机器人控制、汽车导航、电力系统等。

下面将以一个模拟小车控制的实例来介绍如何利用Matlab进行模糊控制。

假设有一个小车需要根据距离和角度来控制其行驶方向和速度。

首先要定义输入和输出变量，这里我们将距离划分为近、中、远三个模糊集，角度划分为左、中、右三个模糊集，行驶方向划分为左转、直行、右转三个模糊集，行驶速度划分为慢、中、快三个模糊集。

引用如何在MATLAB下把模糊推理系统转化为查询表(原创)Matlab 2009-12-26 22:05:01 阅读161 评论0 字号：大中小订阅引用foundy的如何在MATLAB下把模糊推理系统转化为查询表(原创)李会先摘要：该文论述了将MATLAB下调试成功的模糊逻辑转换为查询表的一种技巧，这种技巧不直接使用MATLAB的矩阵计算方法，操作者多数情况下只需点击鼠标就可完成任务，效率比较高，该方法使用MATLAB下的系统测试工具，收集构造查询表所需的数据资料，文中以MATLAB中的水位模糊控制演示模型为例，把该系统的模糊控制推理模块用在其基础上生成的查询表代替后再进行水位控制仿真，控制效果与模糊推理模块在线推理控制是一致的。

关键词：模糊控制;查询表;MATLAB;Simulink; 系统测试Abstract：This article discuss a skill that make a translation from fuzzy logic system to Lookup Table in Matlab,It doesn't use matrix computing, user need only to drag and draw the mouse completing this task,It's a efficiency method which to collect data for Lookup Table construction from a fuzzy controller by SystemTest Toolbox in Matlab,in the article,I will discuss the skill by a demo which is the Water Level Control in Tank in the Fuzzy logic Toolbox,at last,I simulate the Water Control in Tank instead of the Fuzzy Controller with the Lookup Table which I have constructed,the test results is verywell.Keywords: Fuzzy Logic, Matlab,Simulink,Lookup Table,SystemTest1. 引言在MATLAB/Simulink下，构建模糊逻辑系统模型和调试其推理规则都是很方便的[3][4]，我们当然不希望在MATLAB下的仿真工作仅仅用于仿真目的，如果实际产品设计能继承仿真的工作成果，将事半功倍。

m a t l a b计算模糊控制表(总8页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--Matlab计算模糊控制表实现程序如下：clc; %清空命令窗口clear; %清空工作空间e=[1,,,,,0,0,0,0,0,0,0,0;,,1,,,0,0,0,0,0,0,0,0;0,,,,1,,,0,0,0,0,0,0;0,0,0,0,,,1,0,0,0,0,0,0;0,0,0,0,0,0,1,,,0,0,0,0;0,0,0,0,0,0,,,1,,,,0;0,0,0,0,0,0,0,0,,,1,,;0,0,0,0,0,0,0,0,,,,,1] %误差的隶属度函数表，8*13的矩阵eb=[1,,,0,0,0,0,0,0,0,0,0,0;,,1,,,0,0,0,0,0,0,0,0;0,0,,,1,,,0,0,0,0,0,0;0,0,0,0,,,1,,,0,0,0,0;0,0,0,0,0,0,,,1,,,0,0;0,0,0,0,0,0,0,0,,,1,,;0,0,0,0,0,0,0,0,0,0,,,1] %误差变化率的隶属度函数表，7*13的矩阵；u=[1,,,0,0,0,0,0,0,0,0,0,0;,,1,,,0,0,0,0,0,0,0,0;0,0,,,1,,,0,0,0,0,0,0;0,0,0,0,,,1,,,0,0,0,0;0,0,0,0,0,0,,,1,,,0,0;0,0,0,0,0,0,0,0,,,1,,;0,0,0,0,0,0,0,0,0,0,,,1] %输出控制量u,7*13的矩阵；rulelist=[1,1,1,1,2,4,4;1,1,1,1,2,4,4;2,2,2,2,4,5,5;2,2,3,4,5,6,6;2,2,3,4,5,6,6;3,3,4,6,6,6,6;4,4,6,7,7,7,7;4,4,6,7,7,7,7] %控制规则表，为8*7=56条规则；for ey=1:13 % 输入变量e的13个取值：-6——6；for eby=1:13 %输入变量eb的13个取值：-6——6；for ex=1:8 % 输入变量e的8个语言变量NB----PB;for ebx=1:7 % 输入变量eb的7个语言变量NB---PB;arule=rulelist(ex,ebx); %取一条规则；C=u(arule,:);%取这条规则的C的隶属度；代表取一行A=e(ex,:);%取这条规则的A的隶属度；代表取一行for i=1:13;for j=1:13;if (A(i)>C(1,j));Ra(i,j)= C(1,j);elseRa(i,j)=A(i);endendend% 算A—C的蕴含关系；AP=zeros(1,13);AP(1,ey)=e(ex,ey);for i=1:13;for j=1:13;if (AP(j)>Ra(j,i));GDA(j,i)= Ra(j,i);elseGDA(j,i)=AP(j);endendend%求合成运算开始的取小；for i=1:13;max=GDA(1,i);for j=1:13;if (max<GDA(j,i))max= GDA(j,i);endendCPA(i)=max;end % 合成运算取大结束；CPA算出来了；arule=rulelist(ex,ebx); %取一条规则；C=u(arule,:);%取这条规则的C的隶属度；代表取一行B=eb(ebx,:);%取这条规则的A的隶属度；代表取一行for i=1:13;for j=1:13;if (B(i)>C(1,j));Rb(i,j)= C(1,j);elseRb(i,j)=B(i);endendend% 算B—C的蕴含关系；BP=zeros(1,13);BP(1,eby)=eb(ebx,eby);for i=1:13;for j=1:13;if (BP(j)>Rb(j,i));GDB(j,i)= Rb(j,i);elseGDB(j,i)=BP(j);endendend%求合成运算开始的取小；for i=1:13;max=GDB(1,i);for j=1:13;if (max<GDB(j,i))max= GDB(j,i);endendCPB(i)=max;end; % 合成运算取大结束；CPB算出来了；for i=1:13if(CPA(i)>CPB(i))CP(i)=CPB(i);elseCP(i)=CPA(i);endend % 第一个CP1计算结束；将来C是56*13的矩阵；CB((ex-1)*7+ebx,:)=CP;endendfor i=1:13;max=CB(1,i);for j=1:56;if(max<CB(j,i))max=CB(j,i);endendU(i)=max;end %56个CP整理结束；sumFZ=0;sumFM=0;for i=1:13;sumFZ=sumFZ+(i-7)*U(i);sumFM=sumFM+U(i);endcore=sumFZ/sumFM;UB(ey,eby)=core; % 一个控制表中的元素算出来了endendUB=round(UB*100)/100;%保留两位display(UB);程序运行结果如下：程序结果分析：综合MATLAB程序运算出来的结果和智能控制理论与技术（孙增圻）第二版上的结果，完全一致，证明程序运算结果正确！。

引用如何在MATLAB下把模糊推理系统转化为查询表(原创) Matlab 2009-12-26 22:05:01 阅读161 评论0 字号：大中小订阅引用foundy的如何在MATLAB下把模糊推理系统转化为查询表(原创)李会先摘要：该文论述了将MATLAB下调试成功的模糊逻辑转换为查询表的一种技巧，这种技巧不直接使用MATLAB的矩阵计算方法，操作者多数情况下只需点击鼠标就可完成任务，效率比较高，该方法使用MATLAB下的系统测试工具，收集构造查询表所需的数据资料，文中以MATLAB中的水位模糊控制演示模型为例，把该系统的模糊控制推理模块用在其基础上生成的查询表代替后再进行水位控制仿真，控制效果与模糊推理模块在线推理控制是一致的。

关键词：模糊控制;查询表;MATLAB;Simulink; 系统测试Abstract：This article discuss a skill that make a translation from fuzzy logic system to Lookup Table in Matlab,It doesn't use matrix computing, user need only to drag and draw the mouse completing this task,It's a efficiency method which to collect data for Lookup Table construction from a fu zzy controller by SystemTest Toolbox in Matlab,in the article,I will discuss the skill by a demo which is the Water Level Control in Tank in the Fuzzy logic Toolbox,at last,I simulate the Water Control in Tank instead of the Fuzzy Controller with the Lookup Table which I have constructed,the test results is verywell.Keywords: Fuzzy Logic, Matlab,Simulink,Lookup Table,SystemTest1. 引言在MATLAB/Simulink下，构建模糊逻辑系统模型和调试其推理规则都是很方便的[3][4]，我们当然不希望在MATLAB下的仿真工作仅仅用于仿真目的，如果实际产品设计能继承仿真的工作成果，将事半功倍。

实例：MATLABSimulink实现模糊PID控制被控对象：Ts = 0.1;Plant = c2d(zpk([],[-1 -3 -5],1),Ts); %零极点模型，并离散化根据对象Plant，确定PID参数：C0 = pid(1,1,1,'Ts',Ts,'IF','B','DF','B'); % 定义PID结构C = pidtune(Plant,C0) %对PID参数进行优化[Kp, Ki, Kd] = piddata(C); % 输出参数得出PID结构及其参数值：接下来根据求出的PID参数确定GCE、GE 、GCU 和GU的取值：由模糊PID控制结构可得如下等式：Kp = GCU * GCE + GU * GEKi = GCU * GEKd = GU * GCE形式转换如下：GE = 10; %根据模糊控制的论语直接确定GCE = GE*(Kp-sqrt(Kp^2-4*Ki*Kd))/2/Ki=3.4285;GCU = Ki/GE=2.8631;GU = Kd/GCE=2.0138;模糊PID控制系统结构（连续模糊控制器）：图中的离散时间积分和微分块直接调用。

模糊控制器输入输出结构：模糊控制器输入输出隶属度函数：模糊控制器规则表：模糊控制器规则曲面图：连续模糊PID控制器，仿真结果：模糊PID控制系统结构（离散模糊控制器）：离散模糊控制器查询表：离散模糊PID控制器，仿真结果：主要代码如下：（1）、对象模型：Ts = 0.1;Plant = c2d(zpk([],[-1 -3 -5],1),Ts);（2）、PID参数优化：C0 = pid(1,1,1,'Ts',Ts,'IF','B','DF','B');C = pidtune(Plant,C0)[Kp, Ki, Kd] = piddata(C);（3）、比例因子确定：GE = 10;GCE = GE*(Kp-sqrt(Kp^2-4*Ki*Kd))/2/Ki;GCU = Ki/GE;GU = Kd/GCE;（4）、连续模糊PID控制建立：FIS = newfis('FIS','sugeno');%%% 定义输入E:FIS = addvar(FIS,'input','E',[-10 10]);FIS = addmf(FIS,'input',1,'Negative','gaussmf',[7 -10]); FIS = addmf(FIS,'input',1,'Positive','gaussmf',[7 10]); %%% 定义输入CE:FIS = addvar(FIS,'input','CE',[-10 10]);FIS = addmf(FIS,'input',2,'Negative','gaussmf',[7 -10]); FIS = addmf(FIS,'input',2,'Positive','gaussmf',[7 10]); %%% 定义输出u:FIS = addvar(FIS,'output','u',[-20 20]);FIS = addmf(FIS,'output',1,'Min','constant',-20);FIS = addmf(FIS,'output',1,'Zero','constant',0);FIS = addmf(FIS,'output',1,'Max','constant',20);% 定义规则:%% # If |E| is Negative and |CE| is Negative then |u| is -20 % # If |E| is Negative and |CE| is Positive then |u| is 0% # If |E| is Positive and |CE| is Negative then |u| is 0% # If |E| is Positive and |CE| is Positive then |u| is 20 ruleList = [1 1 1 1 1;... % Rule 11 2 2 1 1;... % Rule 22 1 2 1 1;... % Rule 32 23 1 1]; % Rule 4FIS = addrule(FIS,ruleList);gensurf(FIS) %生成模糊控制器（5）、离散模糊控制器查询表：Step = 2;E = -10:Step:10;CE = -10:Step:10;N = length(E);LookUpTableData = zeros(N);for i=1:Nfor j=1:N% compute output u for each combination of break points LookUpTableData(i,j) = evalfis([E(i) CE(j)],FIS);endend。

clc;clear;E = [1,0.8,0.7,0.4,0.1,0,0,0,0,0,0,0,0;0.2,0.7,1,0.7,0.3,0,0,0,0,0,0,0,0;0,0.1,0.3,0.7,1,0.7,0.2,0,0,0,0,0,0;0,0,0,0,0.1,0.6,1,0,0,0,0,0,0;0,0,0,0,0,0,1,0.6,0.1,0,0,0,0;0,0,0,0,0,0,0.2,0.7,1,0.7,0.3,0.1,0;0,0,0,0,0,0,0,0,0.2,0.7,1,0.7,0.3;0,0,0,0,0,0,0,0,0.1,0.4,0.7,0.8,1]%%8*13 EC =[1,0.7,0.3,0,0,0,0,0,0,0,0,0,0;0.3,0.7,1,0.7,0.3,0,0,0,0,0,0,0,0;0,0,0.3,0.7,1,0.7,0.3,0,0,0,0,0,0;0,0,0,0,0.3,0.7,1,0.7,0.3,0,0,0,0;0,0,0,0,0,0,0.3,0.7,1,0.7,0.3,0,0;0,0,0,0,0,0,0,0,0.3,0.7,1,0.7,0.3;0,0,0,0,0,0,0,0,0,0,0.3,0.7,1]%%7*13U=[1,0.7,0.3,0,0,0,0,0,0,0,0,0,0;0.3,0.7,1,0.7,0.3,0,0,0,0,0,0,0,0;0,0,0.3,0.7,1,0.7,0.3,0,0,0,0,0,0;0,0,0,0,0.3,0.7,1,0.7,0.3,0,0,0,0;0,0,0,0,0,0,0.3,0.7,1,0.7,0.3,0,0;0,0,0,0,0,0,0,0,0.3,0.7,1,0.7,0.3;0,0,0,0,0,0,0,0,0,0,0.3,0.7,1]%%7*13rulelist= [1,1,1,1,2,4,4;1,1,1,1,2,4,4;2,2,2,2,4,5,5;2,2,3,4,5,6,6;2,2,3,4,5,6,6;3,3,4,6,6,6,6;4,4,6,7,7,7,7;4,4,6,7,7,7,7]%%8*7for iii=1:13 %偏差E的模糊值控制for jjj=1:13 %偏差率EC的模糊值控制for ii=1:8 %偏差E的模糊规则控制for jj=1:7 %偏差变化率EC的模糊规则控制A_rulelist = rulelist(ii,jj); %查模糊规则表%******计算C1A'************A = E(ii,:); %取A'C_A = U(A_rulelist,:); %取Cifor i=1:13 %求R1Afor j=1:13if(A(i) > C_A(1,j))Ra(i,j) = C_A(1,j);elseRa(i,j) = A(i);endendendAA = zeros(1,13); %取AA=A' 如AA=[1,0,0,0,0,0,0,0,0,0,0,0,0]; %AA(1,iii) = E(ii,iii);AA(1,iii) = 1;for i=1:13 %先取小for j=1:13if(AA(j) > Ra(j,i))A_qux(j,i) = Ra(j,i);elseA_qux(j,i) = AA(j);endendendfor i=1:13 %再取大，，，求和CiAmax = A_qux(1,i);for j=1:13if(max < A_qux(j,i))max = A_qux(j,i);endendCiA(i) = max;end%********CiA计算完毕*********%*******计算CiB'*************B = EC(jj,:); %取B' ???C_B = U(A_rulelist,:); %取Ci ??? for i=1:13 %求R1Bfor j=1:13if(B(1,i) > C_B(1,j))Rb(i,j) = C_B(1,j);elseRb(i,j) = B(1,i);endendendBB = zeros(1,13); %取BB=B' 如BB=[1,0,0,0,0,0,0,0,0,0,0,0,0]; %BB(1,jjj) = EC(jj,jjj);BB(1,jjj) = 1;for i=1:13 %先取小for j=1:13if(BB(j) > Rb(j,i))B_qux(j,i) = Rb(j,i);elseB_qux(j,i) = BB(j);endendendfor i=1:13 %再取大，，，求和CiAmax = B_qux(1,i);for j=1:13if(max < B_qux(j,i))max = B_qux(j,i);endendend%*******计算CiB'完毕****%*******计算C1'=CiA'交CiB'*********for i=1:13if CiA(i) > CiB(i)Ci(i) = CiB(i);elseCi(i) = CiA(i);endend%*******计算C1'完毕************C((ii-1)*7+jj,:) = Ci; % 将Ci存到数组C中，C是56*13的数组endend%根据式Ui=C'=C1'并C2'并……并C56'for i=1:13max = C(1,i);for j=1:56max = C(j,i);endendUi(i) = max;end%用重心法进行解模糊运算,并映射为实际的控制量sum_fenz = 0;sum_fenm = 0;for i=1:13sum_fenz = sum_fenz + (i-7)*Ui(i);sum_fenm = sum_fenm + Ui(i);endcore = sum_fenz/sum_fenm;U_control(iii,jjj) = core;endendU_control = round(U_control.*10000)/10000; %对控制量保留小数点后两位。

用模糊控制实现水箱水温的恒温控制。

水箱由底部的电阻性电热元件加热，由电动搅拌器实现均温.设控制的目标温度为25ºC,以实测温度T与目标温度R之差，即误差e=T-R,以及误差变化率ec为输入，以固态继电器通电时间的变化量u（以一个控制周期内的占空比表示，控制电加热器的功率）为输出.设e的基本论域为[-5，5] ºC，其语言变量E的论域为[-5，5］；ec的基本论域为［-1,1] ºC/s，其语言变量EC的论域为［—5，5］;控制量u的基本论域为[—5，5］单位，其语言变量U的论域为[—5，5］。

E、EC和U都选5个语言值{NB，NM，NS，Z,PS，PM,PB}，各语言值的隶属函数采用三角函数,其分布可用表1和表2表示,控制规则如表3所示。

要求:1、画出模糊控制程序流程图；2、计算出模糊控制器的查询表，写出必要的计算步骤。

表1 语言变量E、EC的赋值表表2 语言变量U的赋值表解：步骤：1)输入输出语言变量的选择。

输入变量选为实测温度T与目标温度R之差，即误差e，及误差变化率ec；输出语言变量选固态继电器通电时间的变化量u，故模糊控制系统为双输入—单输出的基本模糊控制器.2)建立各语言变量的赋值表。

设误差e的基本论域为［-5，5］.C,输入变量E的论域为[-5,—4，-3，—2,-1，0,1，2,3,4，5］，误差的量化因子为ke=5/5=1。

语言变量E选取5个语言值：PB PS ZE NS NB。

表1为语言变量E、EC的赋值表，表2为语言变量U的赋值表,,,,表1语言变量E、EC的赋值表表2 语言变量U的赋值表3)建立模糊控制规则表,总结控制策略，得出一组由25条模糊条件语句构成的控制规则，据此建立模糊控制规则表，如表3所示.表中行与列交叉处的每个元素及其所在列的第一行元素和所在行的第一列元素，对应于一个形式为”if E and EC then U”的模糊语句，根据该模糊语句可得相应的模糊关系i R ,则总控制规则的总模糊关系为251=i i R U R =。

MATLAB环境下的模糊推理程序化方法关键词：模糊操纵近似推理模糊推理程序化模糊操纵具有不依靠对象的数学模型、鲁棒性强、能够专门好地克服传动系统中模型参数变化和非线性等不确定因素的优点,因此,模糊操纵在实际操纵系统中得到广泛应用。

模糊操纵器普遍采纳的是离线进行模糊推理产生的模糊操纵表,然后把操纵表储备在单片机中进行在线查表操纵,但模糊推理运算量大,这给模糊操纵器的设计和调整带来了许多困难。

此外,模糊操纵存在的一个较大的缺点是稳态精度不高。

为此,人们提出了许多改进的方法[１],其中最直截了当的方法是增加模糊量化论域。

然而,当量化论域中元素、操纵规则的条数专门多时,模糊推理运算操纵表的运算量大大增加。

本文在ＭＡＴＬＡＢ环境下,研究了模糊推理算法,研制了模糊推理程序。

只要给出模糊操纵器的输入和输出量的隶属函数矩阵、操纵规则矩阵、模糊量的特点向量矩阵,运行该程序就可得到模糊操纵表。

该软件使用方便,为模糊操纵的研究和应用提供了方便的条件。

１模糊推理概述在模糊操纵中,关键是要求得模糊关系矩阵,应用最多的是离线进行模糊推理产生操纵表,模糊推理是模糊操纵器的核心。

那个地点以两入一出、采纳ＣＲＩ推理方法及重心法解模糊的模糊操纵器为例,简要介绍模糊推理过程。

设模糊集合Ａｉ＝（ａ１ｉ．．．ａｎｉ）∈Ｆ(Ｘ),Ｂｉ＝（ｂ１ｉ．．．ｂｍｉ）∈Ｆ(Ｙ),Ｃ＝（ｃ１ｉ．．．ｃｔｉ）∈Ｆ(Ｚ) (ｉ＝１,．．．,ｐ),模糊规则为“ＩＦＡｉＡＮＤＢｉＴＨＥＮＣｉ”（ｉ＝１,．．．,ｐ）。

其中ｐ为模糊变量的个数,Ｆ（Ｘ）、Ｆ（Ｙ）、Ｆ（Ｚ）分不为论域Ｘ、Ｙ、Ｚ上的模糊集。

由此可求得总模糊关系：对某一模糊特点向量Ａ*、Ｂ*,进一步可求出输出的模糊量：最后,通过解模糊判决可求出输出的精确量:注：Ａｉ×Ｂｉ是模糊向量的笛卡儿积,由公式（４）运算：其中,“Ｔ”表示转置,“ｏ”表示矩阵合成运算,使用最常见的“∨—∧”算子运算,见公式：那个地点需要指出的是,把笛卡儿乘积看作一个ｎ×１与一个１×ｍ的矩阵合成。

Matlab 的 Fuzzy 工具箱实现模糊控制(rulelist的确定)用 Matlab 的 Fuzzy 工具箱实现模糊控制- -用 Matlab 中的 Fuzzy 工具箱做一个简单的模糊控制，流程如下：1、创建一个 FIS (Fuzzy Inference System ) 对象，a = newfis(fisName,fisType,andMethod,orMethod,impMethod, aggMethod,defuzzMethod)一般只用提供第一个参数即可，后面均用默认值。

2、增加模糊语言变量a = addvar(a,'varType','varName',varBounds)模糊变量有两类：input 和 output。

在每增加模糊变量，都会按顺序分配一个 index，后面要通过该 index 来使用该变量。

3、增加模糊语言名称，即模糊集合。

a = addmf(a,'varType',varIndex,'mfName','mfType',mfParams)每个模糊语言名称从属于一个模糊语言。

Fuzzy 工具箱中没有找到离散模糊集合的隶属度表示方法，暂且用插值后的连续函数代替。

参数 mfType 即隶属度函数(Membership Functions)，它可以是 Gaussmf、trimf、trapmf等，也可以是自定义的函数。

每一个语言名称也会有一个 index，按加入的先后顺序得到，从 1 开始。

4、增加控制规则，即模糊推理的规则。

a = addrule(a,ruleList)其中 ruleList 是一个矩阵，每一行为一条规则，他们之间是 ALSO 的关系。

假定该 FIS 有 N 个输入和 M 个输出，则每行有 N+M+2 个元素，前 N 个数分别表示 N 个输入变量的某一个语言名称的 index，没有的话用 0 表示，后面的 M 个数也类似，最后两个分别表示该条规则的权重和个条件的关系，1 表示 AND，2 表示 OR。

基于Matlab的模糊查询表生成方法探讨
叶伊莎;任佳
【期刊名称】《实验室研究与探索》
【年(卷),期】2014(033)005
【摘要】模糊查询表是模糊控制器的一种离线对等表格,该表描述了输入的偏差、偏差变化量与控制的输出之间一一对应的关系.为便于相关专业的本科生深入了解模糊查询表,进一步学习掌握模糊查询表并进行拓展应用,本文对基于Matlab的模糊查询表三种生成方法进行了探讨.本文以简单的单回路控制系统为例,分别阐述了逐个代入计算法、TOOL测试向量生成法和M文件编译法这三种模糊查询表的生成方法.通过探讨与仿真,对三者的优缺点进行了简单的总结.
【总页数】6页(P101-106)
【作者】叶伊莎;任佳
【作者单位】浙江理工大学自动化系,浙江杭州310018;浙江理工大学自动化系,浙江杭州310018
【正文语种】中文
【中图分类】TP273
【相关文献】
1.基于MATLAB生成模糊控制规则离线查询表 [J], 刘淑荣;金波
2.基于生成式对抗网络的结构化数据表生成模型 [J], 宋珂慧; 张莹; 张江伟; 袁晓洁
3.基于MATLAB编程的弗兰克-赫兹实验数据处理方法探讨 [J], 李立; 张皓晶; 张
雄
4.MathWorks推出基于MATLAB生成HDL代码的产品新产品支持利用MATLAB和Simulink生成HDL代码和验证 [J],
5.土地利用规划中用地平衡表自动化生成方法探讨 [J], 杨得志;王杰臣
因版权原因，仅展示原文概要，查看原文内容请购买。

基于Matlab模糊控制器HDL代码的自动生成诸葛俊贵【摘要】This article, taking the Water Level Control in a Tank as an example, proposes a fuzzy controller automatic HDL code generation method based on Matlab. The generated code can be ported to the FPGA control system. The method is divided into four steps ：（ 1 ） The fuzzy controller is designed using Fuzzy Logic Toolbox in the Matlab. （2） The fuzzy controller is transformed into the form of Lookup Table. （3） The controller Lookup table is implemented with the state machine. （4） The fuzzy controller implementation with state machine was translated into HDL code by HDL Coder.%以水箱液位控制为例，提出了一种基于Maflab的模糊控制器HDL代码自动生成方法，生成的代码可以移植到FPGA控制系统上。

该方法分4个步骤：（1）利用Maflab的FuzzyLogic工具箱设计模糊控制器。

（2）将模糊控制器转换为LookupTable的形式。

（3）将制作好的控制器查找表用状态机实现。

（4）用HDLCoder将状态机实现的模糊控制器翻译成HDL代码。

【期刊名称】《电子科技》【年(卷),期】2012(025)001【总页数】4页(P42-44,47)【关键词】FPGA;Matlab;Simulink;模糊控制器;Lookup;Table;状态机;HDL;Coder【作者】诸葛俊贵【作者单位】上海师范大学精密机电系统与控制工程研究室,上海201418【正文语种】中文【中图分类】TP273.4经典和现代控制理论都是建立在被控对象具有精确数学模型的基础上，而实际应用中的许多系统很难用精确的数学模型来描述，难以建模，无法确定控制过程的传递函数和状态方程［1］。

MATLAB实现模糊控制⼀、简介MATLAB软件有提供⼀个模糊推理系统编辑器，利⽤模糊⼯具箱在matlab命令窗⼝输⼊Fuzzy命令进⼊模糊控制编辑环境⼆、主要步骤1、接受输⼊变量2、输⼊变量模糊化3、利⽤模糊规则进⾏推理得出结论4、综合步骤3利⽤结论从模糊⾪属度得到实际的输出值5、输出结果三、MATLAB运⾏结果输⼊ e 的模糊语⾔变量及其⾪属度函数：输⼊ ec 的模糊语⾔变量及其⾪属度函数：输出结果：四、总结在本次实验中设置了两个模糊输⼊变量（e和ec),⼀个模糊输出变量u 。

在规则库中建⽴了7x7=49条规则，模糊规则中第⼀个和第⼆个为输⼊，第三个数表输出，后俩个数分别是规则权重和AND OR选项。

模糊变量的⾪属函数分别设置成了“Z型”、“三⾓形”、“S型”五、代码部分%模糊控制器设计a=newfis('fuzzf'); %创建新的模糊推理系统%输⼊1f1=1;a=addvar(a,'input','e',[-6*f1,6*f1]);%添加 e 的模糊语⾔变量a=addmf(a,'input',1,'NB','zmf',[-6*f1,-2*f1]);%添加 e 的模糊语⾔变量的⾪属度函数（z型）a=addmf(a,'input',1,'NM','trimf',[-6*f1,-4*f1,-1]);%⾪属度函数为三⾓形a=addmf(a,'input',1,'NS','trimf',[-6*f1,-2*f1,1*f1]);a=addmf(a,'input',1,'Z','trimf',[-4*f1,0,4*f1]);a=addmf(a,'input',1,'PS','trimf',[-2*f1,0*f1,2*f1]);a=addmf(a,'input',1,'PM','trimf',[0,4*f1,6*f1]);a=addmf(a,'input',1,'PB','smf',[2*f1,6*f1]);%输⼊2f2=1;a=addvar(a,'input','ec',[-6*f2,6*f2]);%添加 ec 的模糊语⾔变量a=addmf(a,'input',2,'NB','zmf',[-6*f2,-2*f2]);a=addmf(a,'input',2,'NM','trimf',[-6*f2,-4*f2,-1]);a=addmf(a,'input',2,'NS','trimf',[-6*f2,-2*f2,1*f2]);a=addmf(a,'input',2,'Z','trimf',[-4*f2,0,4*f2]);a=addmf(a,'input',2,'PS','trimf',[-2*f2,0*f2,2*f2]);a=addmf(a,'input',2,'PM','trimf',[0,4*f2,6*f2]);a=addmf(a,'input',2,'PB','smf',[2*f2,6*f2]);%输出f8=1.5;a=addvar(a,'output','u',[-6*f8,6*f8]);%添加 u 的模糊语⾔变量a=addmf(a,'output',1,'NB','zmf',[-6*f8,-2*f8]);a=addmf(a,'output',1,'NM','trimf',[-6*f8,-4*f8,-1]);a=addmf(a,'output',1,'NS','trimf',[-6*f8,-2*f8,2*f8]);a=addmf(a,'output',1,'Z','trimf',[-4*f8,0,4*f8]);a=addmf(a,'output',1,'PS','trimf',[-2*f8,0*f8,6*f8]);a=addmf(a,'output',1,'PM','trimf',[1,4*f8,6*f8]);a=addmf(a,'output',1,'PB','smf',[2*f8,6*f8]);%规则库rulelist=[11111; %编辑模糊规则，后俩个数分别是规则权重和AND OR选项12111;13111;14211;15211;16311;17411;21111;22211;23211;24211;25311;26411;27511;31711;32611;33511;34411;35311;36211;37111;41711;42611;43511;44411;45311;46211;47111;51711;52611;53511;54411;55311;56211;57111;61711;62611;63511;64411;65311;66211;67111;71711;72611;73511;74411;75311;76211;77111;];a=addrule(a,rulelist); %添加模糊规则函数showrule(a) %显⽰模糊规则函数a1=setfis(a,'DefuzzMethod','centroid'); %设置解模糊⽅法writefis(a1,'fuzzf'); %保存模糊系统a2=readfis('fuzzf'); %从磁盘读出保存的模糊系统disp('fuzzy Controller table:e=[-3,+3],ec=[-3,+3]');%显⽰矩阵和数组内容%推理Ulist=zeros(7,7); %全零矩阵for i=1:7for j=1:7e(i)=-4+i;ec(j)=-4+j;Ulist(i,j)=evalfis([e(i),ec(j)],a2); %完成模糊推理计算 endend% Ulist=ceil(Ulist) %朝正⽆穷⽅向取整 Ulist %朝正⽆穷⽅向取整%画出模糊系统figure(1); plotfis(a2);figure(2);plotmf(a,'input',1);figure(3);plotmf(a,'input',2);figure(4);plotmf(a,'output',1);。

引用如何在MATLAB下把模糊推理系统转化为查询表(原创)Matlab 2009-12-26 22:05:01 阅读161 评论0 字号：大中小订阅引用foundy的如何在MATLAB下把模糊推理系统转化为查询表(原创)李会先摘要：该文论述了将MATLAB下调试成功的模糊逻辑转换为查询表的一种技巧，这种技巧不直接使用MATLAB的矩阵计算方法，操作者多数情况下只需点击鼠标就可完成任务，效率比较高，该方法使用MATLAB下的系统测试工具，收集构造查询表所需的数据资料，文中以MATLAB中的水位模糊控制演示模型为例，把该系统的模糊控制推理模块用在其基础上生成的查询表代替后再进行水位控制仿真，控制效果与模糊推理模块在线推理控制是一致的。

关键词：模糊控制;查询表;MATLAB;Simulink; 系统测试Abstract：This article discuss a skill that make a translation from fuzzy logic system to Lookup Table in Matlab,It doesn't use matrix computing, user need only to drag and draw the mouse completing this task,It's a efficiency method which to collect data for Lookup Table construction from a fuzzy controller by SystemTest Toolbox in Matlab,in the article,I will discuss the skill by a demo which is the Water Level Control in Tank in the Fuzzy logic Toolbox,at last,I simulate the Water Control in Tank instead of the Fuzzy Controller with the Lookup Table which I have constructed,the test results is verywell.Keywords: Fuzzy Logic, Matlab,Simulink,Lookup Table,SystemTest1. 引言在MATLAB/Simulink下，构建模糊逻辑系统模型和调试其推理规则都是很方便的[3][4]，我们当然不希望在MATLAB下的仿真工作仅仅用于仿真目的，如果实际产品设计能继承仿真的工作成果，将事半功倍。

查询表式模糊逻辑控制器设计实验报告
一、 实验目的
利用Matlab 软件实现模糊控制系统仿真实验，了解模糊控制的查询表方法的基本原理及实现过程，并找出参数Ke ，Kec ，和Ku 对模糊控制器性能影响的规律。

二、 实验要求 设计一个二维模糊控制器分别控制一一个一阶被控对象1
1)(11+=s T s G 。

先用模糊控制器进行控制，然后改变控制对象参数的大小，观察模糊控制的鲁棒性，找出参数Ke ，Kec ，和Ku 对模糊控制器性能影响的规律。

三、 实验步骤
叙述查询表式模糊控制系统仿真主要步骤。

四、实验内容
（一）查询表式模糊控制系统仿真实验
1、一阶对象1
1)(11+=s T s G 采用查询表式方法进行仿真实验，自己选定Ke ，Ku ，Kec 的值，按下表中给出的数值调整被控对象参数并观察输出响应曲线，观察模糊控制器对被控对象参数变化的适应性。

（其中T1称为被控对象参数，Ke ，Ku ，Kec 称为控制器参数）
2变其中的一个控制参数通过仿真实验观察它们各自对控制性能的影响。

将实验结果填入下表。

（1）Ke ＝ Ku ＝
（二）实验讨论
1、通过对模糊控制器参数的设置及调整所获得的控制性能，得出关于控制
器参数对其性能影响的基本规律。

]
1、改变被控对象的参数，考察模糊控制器对被控对象参数变化的适应性，
并得出结论。