展开与折叠(正方体的展开图)

正方体、长方体的展开图与折叠学习目标：1、知识与技能目标：通过展开与折叠活动，认识了长方体、正方体的不同的展开图，加深对长方体、正方体的认识，感受立体图形与平面图形的关系，建立长方体或正方体中的面与展开图中的面的对应关系。

2、过程与方法目标：在想象、操作等活动中，经历和体验立体图形与平面图形的相互转化过程，渗透转化和对应的数学思想，发展空间观念，培养学生多角度探究问题的能力和空间思维能力，积累数学活动经验。

3、情感态度价值观目标：激发学生对探索知识的强烈愿望和对数学学习的兴趣，并不断体验数学活动中探索过程和创造过程带来的乐趣，建立正确的数学学习观。

教学过程：第一课时活动一：复习长方体和正方体的特征。

引导学生根据提问回答问题。

1、出示长方体盒子，师问：长方体有几个顶点？几个面？几条棱？它的面和棱各有什么特点？2、再出示一个正方体盒子，师问：正方体又有几个顶点？几个面？几条棱？它的面和棱各有什么特点？3、师：如果确定了长方体或正方体的其中一个面为底面（下面），你能很快说出其余的五个面各是什么面吗？请同桌的同学互相说一说。

活动二：认识长方体、正方体的展开图：1、师指着长方体盒子问：谁有办法把这个立体图形变成平面图形？怎样剪最好？2、学生动手剪，师指导有困难的学生，并把一个剪得好的长方体展开图展示在黑板上。

3、师指着正方体盒子问：这个正方体的盒子能否剪成这样的平面图形？请同学们试一试。

4、学生继续剪，把一个剪得好的正方体展开图展示在黑板上。

5、师指着黑板上的展开图：像这样沿着长方体或正方体的棱剪开，使这个长方体或正方体完全的展开，得到一个六个面互相连接的平面图形，我们叫做长方体或正方体的平面展开图。

活动三：剪出来的平面展开图和黑板上的展开图不一样，而且周围同学剪出来的展开图也不太一样，这是为什么呢？第二课时：正方体的展开探究一：相同的长方体或正方体，剪出来的展开图为什么会不一样呢？谁来帮忙解决这个问题？小组内讨论交流，自主探索：探究二：回忆一下刚才你是怎么剪的？为什么会不一样呢？把你的剪法和想法与小组内的其他成员交流。

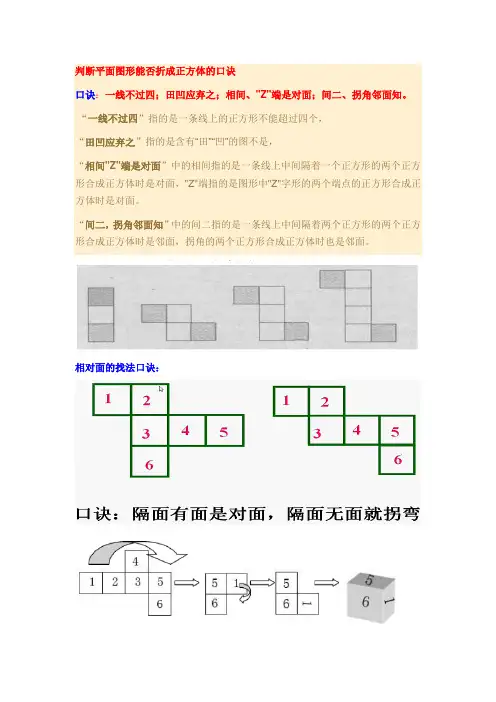
判断平面图形能否折成正方体的口诀口诀：一线不过四；田凹应弃之；相间、"Z"端是对面；间二、拐角邻面知。

“一线不过四”指的是一条线上的正方形不能超过四个，“田凹应弃之”指的是含有“田”“凹”的图不是，“相间"Z"端是对面”中的相间指的是一条线上中间隔着一个正方形的两个正方形合成正方体时是对面，"Z"端指的是图形中"Z"字形的两个端点的正方形合成正方体时是对面。

“间二，拐角邻面知”中的间二指的是一条线上中间隔着两个正方形的两个正方形合成正方体时是邻面，拐角的两个正方形合成正方体时也是邻面。

相对面的找法口诀：第18讲 图形推理-空间重构类-描点法（图形）（流畅）.f4v答案：B 答案：D。

答案：A。

答案：B 答案：C答案：B。

答案：C。

【例题1】（2012年国家）左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成（）一本通解答：由以上性质可以可以看出，一点面和四点面为对立面，B项错误；C项中一点面与六点面构成如图相邻关系时，五点面应位于左面而右顶面（可以六点面为上面折叠），排除；二点面、三点面、四点面三面相邻，且公共顶点不变，三点面方向不对，D项错误。

注：平面图形的公共顶点和公共边折叠成多面体后仍为这三个面的公共顶点和公共边。

（通过上图D项可验证）【例题2】（2010年国家）左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成（）一本通解答：横线面和空白面为对立面，C、D项错误；B项中右面及上面的两条线错误，排除。

【例题3】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？一本通解答：A项三条斜线不可能交于一点，排除。

C项两条水平线不会交于一点，排除。

D项正面应为竖直线，排除。

【例题4】（2008年江苏B类）一本通解答：B。

解法一：三个空白面都不相互对立，是相邻的，B项正确。

解法二：三条对角线不会交于一点，也不会首尾相连，排除C、D两项；前表面和右表面的线段交点应该是在下方，排除A项，所以B项正确。

正方体展开图
图形的展开与折叠对于同学来讲，是一个立体几何向平面几何的转化过程。

对于圆柱、圆锥、棱柱、棱锥而言，其展开图比较单一.而正方体的展开图因其样式多，是同学们在学习的难点。

实际上只要我们认真研究，不难将正方体的展开图归类为以下四类，共11个基本图形，离开了这11个基本图形,其都不会是正方体的展开图（这里应注意的是有的时候是这11个基本图形的翻折、旋转，也属于正方体的展开图）。

具体分类如下：
1．“141型”，中间一行4个作侧面，上下两个各作为上下底面,•共有6种基本图形.
2．“231型"，中间3个作侧面，共3种基本图形.
3．“222"型，两行只能有1个正方形相连。

4．“33”型，两行只能有1个正方形相连.
同学们，你能记住吗，只要记住口诀就成了.。

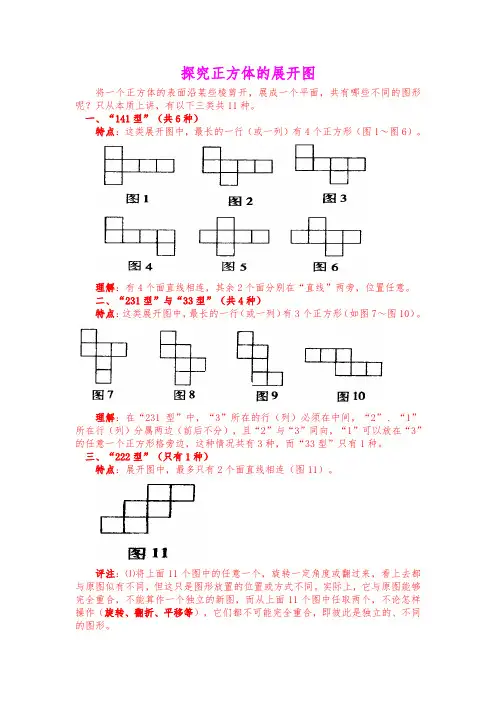
探究正方体的展开图
将一个正方体的表面沿某些棱剪开，展成一个平面，共有哪些不同的图形呢？只从本质上讲，有以下三类共11种。

一、“141型”（共6种）
特点：这类展开图中，最长的一行（或一列）有4个正方形（图1～图6）。

理解：有4个面直线相连，其余2个面分别在“直线”两旁，位置任意。

二、“231型”与“33型”（共4种）
特点：这类展开图中，最长的一行（或一列）有3个正方形（如图7～图10）。

理解：在“231型”中，“3”所在的行（列）必须在中间，“2”、“1”所在行（列）分属两边（前后不分），且“2”与“3”同向，“1”可以放在“3”的任意一个正方形格旁边，这种情况共有3种，而“33型”只有1种。

三、“222型”（只有1种）
特点：展开图中，最多只有2个面直线相连（图11）。

评注：⑴将上面11个图中的任意一个，旋转一定角度或翻过来，看上去都与原图似有不同，但这只是图形放置的位置或方式不同。

实际上，它与原图能够完全重合，不能算作一个独立的新图，而从上面11个图中任取两个，不论怎样操作（旋转、翻折、平移等），它们都不可能完全重合，即彼此是独立的、不同的图形。

⑵对于由大小一样的六个正方形通过边对齐相连组成的平面图，如果图中含有“一”字型、“7”字型、“田”字型、“凹”字型，就一定不能折成正方体。

概括地说，只要不符合上述“141”、“231”和“33”、“222”的特点，就不能折成正方体。

如图12，如果将其看作“231”型，那么，无论怎么看，“2”和“3”都不是同向，故不能折成正方体。

其实，它属于“123”（或“321”）型。

《展开与折叠》
一、正方体的表面展开图共11种，分为4类
A.1-4-1型中间四连方，上下两侧各有一个，共6种。

B.1-2-3型中间三连方，上下两侧分别有2个，1个，共3种。

C.2-2-2型中间二连方，两侧各有两个，只有1种。

D.3-3 型两排各有三个，只有1种。

二、找展开图相对面的方法。

“间一Z端”。

“间一”是指：排在同一条线上的，隔一个正方形对应必是相对的面。

如图(1)的2和4,3和5；图(2)的C和E。

“Z端”是指：Z字两端对应的正方形必是相对的面。

如图(1)的1和6；图(2)的A和D，B和F。

图(1) 图(2)
三、关于展开与折叠我还想告诉你：
(1)有“凹”字或“田”字形的肯定不是正方体展开图。

(2)长方体的展开图只有“141”型，而且图中临边必须相等！
重要提醒：
(1)棱长总和是指12条棱的长度总和；
长方体棱长总＝(长＋宽＋高)×4
正方体棱长总＝棱长×12
(2)表面积是指6个面的面积总和。

长方体表面积＝(长×宽＋长×高＋宽×高)×2
(注意：长、宽、高每两个都要乘一次)正方体表面积＝棱长×棱长×6
(注意：棱长×棱长是一个面的面积)。