带电粒子在磁场中受力的作用

磁场对带电粒子的作用磁场是指存在磁力的区域，而磁力是一种物理力量，能够对带电粒子产生影响。

本文将探讨磁场对带电粒子的作用及其相关原理。

一、洛伦兹力磁场对带电粒子的主要作用是产生洛伦兹力。

洛伦兹力是由磁场和粒子运动速度的向量积所引起的，其大小和方向都与带电粒子的电荷、速度以及磁场的强度和方向有关。

当带电粒子以一定速度穿过磁场时，洛伦兹力垂直于速度方向和磁场方向，并遵循右手定则。

若带电粒子的电荷正负性与速度方向一致，则洛伦兹力垂直于速度和磁场方向向内；若电荷正负性与速度方向相反，则洛伦兹力垂直于速度和磁场方向向外。

洛伦兹力的大小与磁场强度成正比，与带电粒子的电荷量和速度的乘积成正比。

这意味着，在相同的磁场中，电荷量越大或速度越快的粒子所受到的洛伦兹力越大。

二、磁场对运动轨迹的影响由于洛伦兹力的存在，磁场可以改变带电粒子的运动轨迹。

当带电粒子运动速度与磁场相垂直时，洛伦兹力的作用会使粒子偏离原来的直线运动轨迹，进而形成一个圆形轨迹。

这种轨迹称为磁场中的回旋轨道。

回旋轨道的半径与粒子的电荷量、速度以及磁场的强度成正比。

当磁场强度增加时，回旋轨道的半径也会增加；当速度增加时，回旋轨道的半径亦会增加。

需要注意的是，磁场只能改变粒子的运动轨迹，而不能改变粒子的速度。

当粒子进入磁场后，其速度大小保持不变，仅改变方向。

三、粒子在磁场中的稳定性带电粒子在磁场中的稳定性主要取决于洛伦兹力和离心力之间的平衡情况。

洛伦兹力试图将粒子推向轨迹的中心，而离心力试图将粒子推离轨迹的中心。

当洛伦兹力和离心力相等时，粒子将保持在磁场中心的回旋轨道上，保持稳定。

若洛伦兹力大于离心力，粒子将向轨迹中心靠拢；若洛伦兹力小于离心力，粒子将离开回旋轨道。

四、应用与实际意义磁场对带电粒子的作用在物理学研究、电子技术和医学等领域具有广泛的应用和实际意义。

在物理学研究领域，磁场的作用有助于科学家们对带电粒子的运动进行研究，揭示微观世界的奥秘。

在电子技术中，磁场可用于电子设备的控制和操纵。

磁场中的电流与电荷的运动规律在磁场中，电流和电荷的运动规律是一项重要的物理学研究课题。

磁场对电流和电荷具有一定的影响，它们的运动状态与磁场的强弱、方向等因素息息相关。

下面将从电流和电荷的角度分别阐述它们在磁场中的运动规律。

一、电流在磁场中的运动规律电流是由带电粒子的有序运动形成的，而带电粒子在磁场中的运动受到磁力的作用。

具体来说，当电流通过一根导线时，导线中的电子将受到磁场力的作用而受到偏转。

根据右手定则，当右手拇指指向电流的流向方向时，四指的弯曲方向则表示电子在磁场中受到的偏转方向。

这意味着电流方向与磁场方向之间存在一定的关系。

根据洛伦兹力的原理，电流在磁场中受到的力可以表示为 F = BIL，其中F为电流受到的磁场力，B为磁场的磁感应强度，I为电流的大小，L为电流段的长度。

由此可见，电流在磁场中的受力与电流的大小和磁场的强弱相关。

根据上述运动规律，电流在强磁场中会受到较大的偏转力，而在弱磁场中则受到较小的偏转力。

此外，当电流方向与磁场方向垂直时，电流将不受到磁场力的作用，而当电流方向与磁场方向平行时，电流将受到最大的磁场力。

二、电荷在磁场中的运动规律除了电流，单个带电粒子即电荷在磁场中的运动规律也备受关注。

电荷运动受到的磁场力与电流类似，但存在一些细微的差异。

根据洛伦兹力的原理，电荷在磁场中受到的力可以表示为 F = qvB，其中F为电荷受到的磁场力，q为电荷的大小，v为电荷的速度，B为磁场的磁感应强度。

电荷是否受到磁力的作用与电荷的速度方向以及磁场方向之间的夹角有关。

当电荷的速度方向与磁场方向垂直时，电荷将受到最大的磁场力，此时磁力将导致电荷绕磁场弯曲运动；而当电荷的速度方向与磁场方向平行时，电荷将不受到磁场力的作用，继续直线运动。

根据上述运动规律，可以得出结论：电荷在强磁场中受到的磁力更大，导致其运动轨迹更弯曲；而在弱磁场中，电荷的磁场力较小，运动轨迹相对较直。

此外，电荷的运动速度越快，受到的磁场力越大，轨迹越弯曲。

磁场中带电粒子的能量与速度关系分析在物理学中，磁场是一种广泛存在于自然界中的力场。

当带电粒子穿过磁场时，会受到磁力的作用，导致其能量和速度发生变化。

本文将探讨磁场中带电粒子的能量和速度之间的关系。

一、洛伦兹力和带电粒子的运动当带电粒子在磁场中运动时，它会受到洛伦兹力的作用，该力与磁场的强度、电荷的大小以及带电粒子的速度有关。

洛伦兹力的数学表达式如下：F = q(v × B)其中，F为洛伦兹力，q为电荷量，v为带电粒子的速度，B为磁场的磁感应强度。

根据洛伦兹力的方向，带电粒子将偏离原本的运动轨迹，并绕着磁力线进行螺旋运动。

这种螺旋运动又称为洛伦兹运动。

二、磁场对带电粒子的能量影响磁场对带电粒子能量的影响主要体现在两个方面：速度的变化和动能的改变。

1. 速度的变化由于洛伦兹力的作用，带电粒子在磁场中的速度会发生变化。

当带电粒子垂直于磁场运动时，洛伦兹力的方向垂直于速度方向，会改变带电粒子的运动方向，但速度大小保持不变。

当带电粒子与磁场的夹角不为90°时，洛伦兹力会同时改变速度方向和大小。

根据洛伦兹力的数学表达式可知，当速度和磁场方向平行时，洛伦兹力为零，带电粒子不受力作用，速度保持恒定。

2. 动能的改变由于洛伦兹力的作用，带电粒子在磁场中运动时会不断改变其动能。

在垂直于磁场方向的运动中，由于速度方向发生改变，带电粒子将会受到周期性的加速和减速作用，动能也会相应地发生周期性变化。

而在速度和磁场方向平行的运动中，洛伦兹力为零，动能将保持不变。

三、轨道半径与速度之间的关系在磁场中，带电粒子的轨道是一条半径不断变化的圆弧，其半径与速度之间存在一定的关系。

根据运动学的知识，带电粒子在磁场中做匀速圆周运动时，其离心力和洛伦兹力平衡，从而有：F = q(v² / r) = q(v × B)其中，r为带电粒子在磁场中运动的轨道半径，v为其速度，B为磁感应强度。

由此可得：v = rB这个关系表明，带电粒子的轨道半径与速度呈正比，即轨道半径越大，速度也随之增加；反之，轨道半径越小，速度减小。

运动电荷在磁场中的受力分析在物理学中，我们学习了电荷和磁场的相互作用。

其中，最为经典的案例就是运动电荷在磁场中受力的问题。

本文将对运动电荷在磁场中的受力进行分析。

一、洛伦兹力的定义和计算公式当一个带电粒子以速度v在磁场B中运动时，它将受到洛伦兹力的作用。

洛伦兹力的定义是：当一个电荷e的粒子以速度v进入磁感应强度为B的均匀磁场中运动时，它所受的力F与物理量e、v、B之间的关系是：F = e * (v x B)其中，矢量符号x表示向量叉积。

此公式表明，洛伦兹力的大小等于电荷e和速度v的乘积，并且与速度v和磁感应强度B的夹角有关。

二、洛伦兹力的方向根据洛伦兹力公式可以看出，洛伦兹力是一个矢量，其方向与速度v和磁感应强度B的夹角有关。

具体来说，将速度向量v按照右手法则旋转到磁感应强度B的方向上，右手握住v，大拇指指向v，四指弯曲的方向则为洛伦兹力的方向。

三、运动电荷在磁场中的轨迹根据洛伦兹力的方向和大小，我们可以推断出运动电荷在磁场中的轨迹。

当洛伦兹力与电荷的速度方向垂直时，电荷将绕着磁场线圈形成一个圆周运动。

当洛伦兹力与电荷的速度方向平行时，电荷将继续沿着直线运动。

而当洛伦兹力与电荷的速度方向呈45度夹角时，电荷将绕着一条螺旋线运动。

四、洛伦兹力的应用洛伦兹力在物理学中有着广泛的应用，其中最为重要的应用之一就是电磁感应。

当一个导线中的电流通过时，导线中的电子将以一定的速度运动。

根据洛伦兹力的作用，电流中的电子将受到一个向导线的方向垂直的磁场力。

利用这一原理，我们可以实现电磁感应，例如发电机的原理。

此外，洛伦兹力还可以应用于粒子加速器和核物理实验中。

在粒子加速器中，带电粒子在加速过程中会产生磁场，从而受到洛伦兹力的作用，加速到较高的速度。

而在核物理实验中，利用洛伦兹力可以将带电粒子进行加速、定位和探测。

五、运动电荷在非均匀磁场中的受力分析虽然本文主要讨论了运动电荷在均匀磁场中的受力分析，但实际应用中我们也经常会遇到非均匀磁场的情况。

磁场的作用探究磁场对带电粒子的力和磁铁的吸引排斥作用磁场的作用探究——磁场对带电粒子的力和磁铁的吸引排斥作用磁场作为物理学中重要的概念之一，对于带电粒子和磁铁都有着重要的作用。

本文将对磁场对带电粒子的力和磁铁的吸引排斥作用进行探究，并深入理解其原理与机制。

一、磁场对带电粒子的力磁场对带电粒子的力的作用是通过洛伦兹力来实现的。

洛伦兹力是指带电粒子在磁场中受到的力，其方向与速度和磁场方向垂直。

具体表达式为F = qvBsinθ，其中F表示洛伦兹力，q为粒子的电荷量，v为粒子的速度，B为磁场的磁感应强度，θ为速度与磁场方向的夹角。

洛伦兹力的方向可通过右手定则确定。

首先，将右手伸直，将食指指向粒子的速度方向，中指指向磁场方向，那么拇指所指方向即为洛伦兹力的方向。

如果粒子是正电荷，则洛伦兹力指向磁场方向；如果粒子是负电荷，则洛伦兹力与磁场方向相反。

二、磁场对带电粒子的轨迹由于洛伦兹力的作用，带电粒子在磁场中的轨迹将发生偏转。

具体来说，当带电粒子的速度与磁场方向垂直时，粒子将绕着磁场线做匀速圆周运动；当速度与磁场方向不垂直时，粒子将在磁场中遵循螺旋线运动。

带电粒子在磁场中的偏转轨迹受力大小和方向的影响。

当速度越大、电荷量越大、磁感应强度越大时，带电粒子偏转的角度越大。

同时，洛伦兹力的方向始终垂直于速度和磁场方向，这使得粒子的轨迹呈现出相对稳定的形态。

三、磁场对磁铁的吸引排斥作用除了对带电粒子的影响外，磁场还对磁铁产生吸引排斥的作用。

在磁场中，两个磁铁之间会产生磁力，表现为吸引或排斥的效应。

根据磁极的性质，有两种情况：1. 同性相斥：当两个磁铁的南极或北极相朝时，它们之间会产生相互排斥的力。

这是由于同性磁极之间产生的磁场方向相同，从而使得两者之间的洛伦兹力方向相反，产生排斥力。

2. 异性相吸：当两个磁铁的南极和北极相朝时，它们之间会产生相互吸引的力。

这是因为异性磁极之间产生的磁场方向相反，从而使得两者之间的洛伦兹力方向相同，产生吸引力。

磁场中的力和磁矩的计算磁场是物理学中一项重要的概念，它描述了物体周围的磁力场。

在磁场中，物体可能会受到一定的力的作用，同时物体也可能具有磁矩。

本文将详细介绍在磁场中计算力和磁矩的方法。

一、磁场中的力计算1. 线电流在磁场中的力：当一段导线通电时，会形成一个绕线圈的磁场。

在磁场中，线电流会受到力的作用。

根据安培力定律，线电流在磁场中受到的力与导线所在平面垂直，与磁感应强度、电流和线段长度相关。

力的大小可以使用以下公式计算：F = B * I * l * sinθ其中，F表示力的大小，B表示磁感应强度，I表示电流的大小，l表示线段的长度，θ表示线段与磁场方向之间的夹角。

2. 带电粒子在磁场中的力：当带电粒子在磁场中运动时，由于带电粒子的速度与磁场之间存在相互作用，带电粒子会受到力的作用。

根据洛伦兹力定律，带电粒子在磁场中受到的力与电荷、速度和磁场相关。

力的大小可以使用以下公式计算：F = q * v * B * sinθ其中，F表示力的大小，q表示电荷的大小，v表示带电粒子的速度，B表示磁感应强度，θ表示速度矢量与磁场方向之间的夹角。

二、磁场中的磁矩计算1. 线圈的磁矩：当一段导线绕成一个圈形时，称为线圈。

线圈具有磁矩，在磁场中会受到力的作用。

线圈的磁矩可以使用以下公式计算：μ = N * I * A其中，μ表示磁矩的大小，N表示线圈中的匝数，I表示电流的大小，A表示线圈的面积。

2. 磁矩与力矩之间的关系：当磁矩在磁场中受到力的作用时，会产生力矩。

力矩可以使用以下公式计算：τ = μ * B * sinθ其中，τ表示力矩的大小，μ表示磁矩的大小，B表示磁感应强度，θ表示磁矩与磁场方向之间的夹角。

总结：磁场中的力和磁矩计算可以通过安培力定律和洛伦兹力定律来求解。

线电流和带电粒子在磁场中受到的力与磁感应强度、电流、速度以及与磁场的夹角有关。

线圈的磁矩与线圈中的匝数、电流以及线圈的面积相关。

磁矩在磁场中受到的力会产生力矩，力矩的大小与磁矩、磁感应强度以及磁矩与磁场方向的夹角相关。

磁场中带电粒子的动能与动量变化分析磁场是物理学中重要的研究对象之一，它对带电粒子的运动轨迹和能量变化产生显著影响。

本文将分析磁场中带电粒子的动能与动量变化，探讨其物理原理和数学表达。

一、动能与动量的基础知识在理解磁场中带电粒子的动力学变化之前，我们首先需要了解动能和动量的基本概念。

动能是物体由于运动而具有的能量，通常用K表示，其表达式为K=1/2mv²，其中m为物体的质量，v为物体的速度。

动量则是物体运动时所具有的性质，用p表示，其表达式为p=mv。

二、带电粒子在磁场中的受力当带电粒子进入磁场时，由于其带电性质，将受到磁场力的作用。

根据洛伦兹力定律，带电粒子在磁场中所受的力的大小和方向为F=qvBsinθ，其中q为粒子的电量，v为粒子的速度，B为磁感应强度，θ为速度方向与磁感应方向之间的夹角。

三、动能变化的分析由于带电粒子在磁场中受到磁场力的作用，其速度和速度方向都会发生变化，从而导致动能的变化。

当带电粒子与磁场垂直时，磁场力垂直于速度方向，不对动能产生影响，动能保持恒定。

当带电粒子与磁场平行时，磁场力与速度方向平行，从而不做功，动能同样保持恒定。

然而，当带电粒子的速度与磁场方向存在一定角度时，磁场力会对动能产生改变。

根据洛伦兹力定律中的正弦函数，当速度方向与磁场方向夹角为90度时，磁场力最大，达到最大做功。

在这种情况下，带电粒子的动能将会增加。

四、动量变化的分析带电粒子在磁场中受到磁场力的作用，从而导致了动量的变化。

根据牛顿第二定律和洛伦兹力定律，我们可以得到磁场力对动量的改变率的表达式为dp/dt=q(v×B)，其中dp/dt代表动量的变化率。

从上述表达式可以看出，在磁场中，带电粒子的动量并不是守恒的，将受到磁场力的作用而发生变化。

磁场力所引起的动量的变化将随着时间而发生变化。

五、动能与动量变化的定量关系根据牛顿第二定律和动能的定义，我们可以将动能的变化率和动量的变化率联系起来。

磁场对带电粒子的作用力分析磁场是我们日常生活中常见的物理现象之一。

它对带电粒子的作用力也是一项重要的研究课题。

在这篇文章中，我们将深入探讨磁场对带电粒子的作用力，并从不同角度进行分析。

首先，我们需要了解磁场对带电粒子的作用力是如何产生的。

根据洛伦兹力的原理，当带电粒子在磁场中运动时，会受到一个与其速度和磁场强度相关的力。

这个力的方向垂直于带电粒子的速度和磁场的方向，并且大小与带电粒子的电荷量、速度和磁场强度有关。

接下来，我们可以从不同的角度来分析磁场对带电粒子的作用力。

首先，我们可以从力的方向来讨论。

根据洛伦兹力的原理，带电粒子在磁场中的运动轨迹会受到力的作用，使其偏离原来的直线运动轨迹。

这个力的方向垂直于带电粒子的速度和磁场的方向，可以使带电粒子绕磁场线旋转或者沿着磁场线做曲线运动。

其次，我们可以从力的大小来讨论。

根据洛伦兹力的原理，力的大小与带电粒子的电荷量、速度和磁场强度有关。

当带电粒子的电荷量增大时，力的大小也会增大。

当带电粒子的速度增大时，力的大小也会增大。

当磁场强度增大时，力的大小也会增大。

这些因素的变化都会影响到磁场对带电粒子的作用力的大小。

此外，我们还可以从带电粒子的运动状态来讨论磁场对其的作用力。

当带电粒子的速度与磁场的方向垂直时，力的大小最大。

当带电粒子的速度与磁场的方向平行时，力的大小为零。

这是因为当带电粒子的速度与磁场的方向垂直时，力的方向与速度的方向垂直，使带电粒子绕磁场线旋转。

而当带电粒子的速度与磁场的方向平行时，力的方向与速度的方向平行，使带电粒子沿着磁场线做直线运动。

最后，我们可以从实际应用的角度来讨论磁场对带电粒子的作用力。

磁场对带电粒子的作用力在许多领域都有重要的应用。

例如，在电动机中，磁场对带电粒子的作用力可以使电动机转动，并将电能转化为机械能。

在粒子加速器中，磁场对带电粒子的作用力可以使带电粒子加速，并达到高速。

在磁共振成像中，磁场对带电粒子的作用力可以使带电粒子在磁场中产生共振，从而得到图像信息。

磁场对带电粒子轨迹的偏转效应在物理学领域中，我们经常会接触到磁场与带电粒子的相互作用。

这种相互作用产生了一种被称为磁场对带电粒子轨迹的偏转效应。

在这篇文章中，我将介绍磁场对带电粒子的影响机制以及相关的实际应用。

首先，我们需要了解磁场与带电粒子之间的相互作用原理。

根据安培定律，当带电粒子在磁场中运动时，会受到一个垂直于其速度方向和磁场方向的洛伦兹力的作用。

这个力的方向垂直于速度方向和磁场方向，并且大小随着粒子带电量和速度的增加而增加。

洛伦兹力的方向使带电粒子的运动轨迹发生弯曲，即带电粒子受到磁场力的作用而偏转。

实际上，这种偏转效应在很多领域中都有重要的应用。

其中一个典型的例子是粒子加速器。

当带电粒子被加速到高速时，它们在磁场中的偏转效应会使其运动轨迹变得弯曲。

利用这个原理，粒子加速器可以通过调节磁场的大小和方向，来控制带电粒子的运动轨迹，从而将其加速到更高的能量水平。

此外，在医学上也存在磁场对带电粒子轨迹的偏转效应的应用。

例如，在核磁共振成像（MRI）中，通过使用强磁场来对带电粒子（如氢离子）施加一个恒定的力，可以使其运动呈螺旋状，从而产生信号用于成像。

这种技术已经广泛应用于医学诊断领域，成为了一种非侵入性的影像检查方法。

此外，磁场对带电粒子轨迹的偏转效应还在科学研究中扮演着重要的角色。

在高能物理实验中，磁场被用于对带电粒子进行精确的测量和分析。

通过测量带电粒子在磁场中的偏转角度以及轨迹曲线的形状，科学家们能够研究粒子的性质、相互作用以及宇宙中的基本物理规律。

最后，让我们简要探讨一下磁场对带电粒子轨迹的偏转效应的基本过程。

当带电粒子进入磁场区域时，它会受到洛伦兹力的作用，使其运动方向发生变化。

这个偏转角度取决于粒子的电荷量、速度以及磁场的大小。

当粒子的速度越大、电荷量越大或者磁场的强度越大时，其偏转角度也会增大。

除了上述讨论的内容之外，磁场对带电粒子轨迹的偏转效应在许多其他领域也有广泛的应用。

例如，磁共振成像技术在材料科学和地质学中也被使用，用于研究物质的结构和性质。

磁偏转原理
磁偏转原理是指在磁场的作用下，带电粒子受到力的作用而发生偏转的现象。

磁场是由磁场源所产生的，而磁场源可以是磁体或电流产生的。

根据磁场的性质，磁偏转可以分为两种情况：一是在恒定磁场中，带电粒子受到洛伦兹力的作用而发生偏转；二是在变化磁场中，带电粒子受到法拉第电磁感应定律的作用而发生偏转。

在恒定磁场中，根据洛伦兹力的表达式F=qvB sinθ，其中q为带电粒子的电荷量，v为粒子的速度，B为磁感应强度，θ为
速度和磁感应强度之间的夹角。

当带电粒子的速度与磁感应强度存在夹角时，就会受到力的作用而偏转。

带电粒子的偏转方向与速度、磁感应强度和电荷量的关系有关。

在变化磁场中，根据法拉第电磁感应定律，当磁场的变化率相对于时间发生变化时，会在空间中产生感应电场，进而产生感应电流。

而根据奥姆定律，感应电流与电阻之间存在电压关系。

带电粒子在感应电场的作用下，会受到电场力的作用而发生偏转。

磁偏转原理在实际应用中有着广泛的应用。

例如，在粒子加速器中，通过调节磁场的强度和方向，可以控制带电粒子的运动轨迹，从而实现粒子加速的目的。

此外，在医学影像学中，磁共振成像（MRI）技术利用磁偏转原理，通过对人体组织内的氢原子核的磁偏转进行检测和分析，获得人体器官的详细影像。

总之，磁偏转原理是研究磁场与带电粒子相互作用的重要理论基础，具有广泛的应用价值。

磁场对带电粒子的作用力引言：磁场是物质和带电粒子相互作用的重要力量之一。

从电磁学的角度来看，任何带电粒子都会在磁场中受到力的作用。

这种作用力被称为洛伦兹力，是电磁学中的基本概念之一。

在本文中，我们将探讨磁场对带电粒子的作用力的原理、性质以及应用。

一、洛伦兹力的原理洛伦兹力是由荷质比和磁场强度决定的，用公式F = q(v × B)来表示，其中F是作用力，q是带电粒子的电荷量，v是带电粒子的速度，B是磁场强度。

这个公式告诉我们，只有在带电粒子的速度与磁场垂直时，磁场才会对带电粒子产生作用力。

当速度与磁场平行时，带电粒子不会受到任何磁场的作用力。

二、洛伦兹力的性质1. 洛伦兹力的方向：根据右手定则，当带电粒子的速度v垂直于磁场B时，用右手握住带电粒子，让手的四指指向v方向，伸直的拇指指向B方向，作用力的方向就是手指弯曲的方向。

根据这个定则，我们可以判断带电粒子受到的洛伦兹力的方向。

2. 洛伦兹力大小的决定因素：根据洛伦兹力公式F = q(v × B)，我们可以发现洛伦兹力与电荷量、速度和磁场强度都有关。

当电荷量和速度增大时，洛伦兹力也相应增大；而当磁场强度增大时，洛伦兹力也会增大。

这说明洛伦兹力的大小与电荷量、速度和磁场强度之间存在一定的关系。

三、磁场对带电粒子的应用1. 磁场对电子的轨迹控制：在粒子加速器和磁体中，磁场被用来控制带电粒子的轨迹。

通过调节磁场的强度和方向，可以使带电粒子沿着特定的轨迹运动，从而实现对粒子的加速和定位。

2. 电磁铁的工作原理：电磁铁是一种利用磁场对带电粒子产生力的设备。

当通过电磁铁的线圈中通电时，线圈产生的磁场会对带电粒子施加作用力，使其偏离原来的轨迹。

在自动贴标机、电铁车、电磁悬浮列车等设备中，都广泛应用了电磁铁的工作原理。

3. 高能物理实验中的磁场应用：在高能物理实验中，强磁场常常被用来研究带电粒子的性质和相互作用。

例如，通过在磁场中将带电粒子进行偏转，可以研究它们的质量、电荷、自旋等特性。

磁场中的带电粒子运动磁场是指存在磁性物质或通过电流产生的区域。

而带电粒子是指具有电荷的微小粒子，如电子、质子等。

当带电粒子运动于磁场中时，会受到磁力的作用，从而产生特殊的轨迹和运动规律。

1. 磁场的基本概念及磁力的作用磁场是由电荷在运动中产生的特殊磁效应而形成的。

当带电粒子运动于磁场中时，会受到磁力的作用。

磁力的大小与粒子的电荷量、速度以及磁场的强度和方向有关。

2. 带电粒子在匀强磁场中的运动规律带电粒子在匀强磁场中运动的轨迹为圆周轨迹。

根据洛伦兹力的方向，带电粒子受力方向与速度方向垂直，由于受力方向改变，粒子将继续在垂直于速度方向的平面上旋转运动，形成一个圆周。

3. 磁场的影响：磁场的强度和方向对带电粒子运动的影响磁场的强度和方向决定了带电粒子在磁场中的受力情况和运动轨迹。

当磁场越强时，带电粒子所受的磁力越大。

而磁场的方向也会影响磁力的方向，进而改变粒子在磁场中的运动轨迹。

4. 带电粒子在非匀强磁场中的运动规律在非匀强磁场中，带电粒子的运动规律变得更加复杂。

由于磁场的强度和方向会随着位置的不同而变化，带电粒子的运动轨迹则是一条弯曲的线路。

5. 带电粒子的磁场感应现象带电粒子在运动中也会产生磁场感应现象。

根据安培定律，电流在产生磁场的同时，带电粒子受到的磁力也会产生反作用力，导致粒子的运动产生一些特殊现象，如霍尔效应等。

总结：磁场中的带电粒子运动是一个复杂而有趣的物理现象。

通过磁力的作用，带电粒子在磁场中形成特定的轨迹和运动规律。

磁场的强度和方向决定了带电粒子的受力情况和轨迹变化。

带电粒子的磁场感应现象也是研究中的重要内容。

对于这一领域的深入了解，不仅有助于物理学的发展，也具有广泛的应用前景。

磁场中的带电粒子和磁场力的作用磁场在自然界中随处可见，在物理学中有着重要的作用。

当一物体处于磁场中并拥有电荷时，磁场力将发挥作用。

本文将探讨磁场中带电粒子的行为以及磁场力对其的作用。

一、磁场中的带电粒子行为磁场中的带电粒子会受到磁场力的作用，这种力称为洛伦兹力。

根据洛伦兹力的方向决定磁场中带电粒子的运动轨迹。

1.1 带电粒子在磁场中的运动轨迹当带电粒子以一定速度进入磁场时，洛伦兹力会垂直于带电粒子速度的方向，使得带电粒子的运动轨迹发生弯曲。

此弯曲轨迹被称为洛伦兹轨道，它呈螺旋线状。

1.2 粒子在磁场中的速度变化洛伦兹力对带电粒子速度的作用并不改变其速度大小，只改变其速度方向。

这使得带电粒子继续保持匀速直线运动，但方向发生变化。

因此，磁场中的带电粒子呈螺旋线运动，速度大小保持不变。

二、磁场力对带电粒子的作用磁场力是带电粒子在磁场中受到的力，它直接影响带电粒子的运动。

2.1 磁场力的方向磁场力与带电粒子速度和磁场方向相关。

根据右手定则可知，当带电粒子运动方向与磁场方向垂直时，磁场力的方向垂直于带电粒子速度和磁场方向的平面。

2.2 带电粒子在磁场中的受力情况根据洛伦兹力的方向，当带电粒子沿着磁场线方向运动，洛伦兹力垂直于带电粒子速度，使其受到向轴线方向的力，被束缚在磁场线上。

而若带电粒子与磁场线方向呈一定夹角时，洛伦兹力与速度方向之间会存在一个分量，使带电粒子受到径向的力，导致其轨迹发生弯曲。

2.3 对运动带电粒子的影响磁场力对带电粒子的影响是使带电粒子的轨迹发生改变，而不改变其速度大小。

这种影响使带电粒子能够被限制在磁场中的特定区域内运动。

三、应用和实际案例磁场中带电粒子的行为和磁场力的作用对科学技术和实际应用有着重要影响。

3.1 粒子加速器粒子加速器是用来加速带电粒子的大型装置，其中磁场力通过磁铁和磁场线来进行粒子束的控制和加速。

磁场力使粒子按既定轨道进行高速运动，以便用于粒子物理学的研究。

3.2 磁共振成像（MRI）磁共振成像利用磁场力来观察和记录人体内部的结构和器官，是现代医学影像学中常用的技术。

带电粒子在磁场中的运动知识点总结带电粒子在磁场中的运动知识点总结磁场是由具有磁性的物质产生的一种特殊的物理现象。

带电粒子在磁场中的运动是一种经典力学问题，也是研究电磁力学的重要内容之一。

本文将从洛伦兹力和运动方程的角度，总结带电粒子在磁场中的运动知识点。

一、洛伦兹力的定义和表达式当带电粒子运动时，其受到磁场的作用力称为洛伦兹力。

洛伦兹力的大小和方向与带电粒子的电荷量、速度以及磁场的强度和方向有关。

洛伦兹力的表达式为：F = q(v × B)，其中F表示洛伦兹力，q表示带电粒子的电荷量，v表示带电粒子的速度，B表示磁场的磁感应强度。

从表达式可以看出，当带电粒子的速度与磁场的方向相垂直时，洛伦兹力最大，其大小为F = qvB。

当带电粒子的速度与磁场的方向平行时，洛伦兹力为零。

二、带电粒子在均匀磁场中的运动1. 带电粒子在均匀磁场中做圆周运动。

当带电粒子的速度与磁场的方向垂直时，洛伦兹力的方向垂直于速度和磁场，使得带电粒子呈圆周运动。

带电粒子沿着圆周运动的半径越小，则速度越大。

2. 带电粒子在均匀磁场中做螺旋线运动。

当带电粒子的速度既有向心分量又有切向分量时，带电粒子在均匀磁场中做螺旋线运动。

螺旋线的轴线平行于磁场方向，而螺旋线的半径和螺旋线的间距则与带电粒子的质荷比有关。

三、带电粒子在非均匀磁场中的运动在非均匀磁场中，带电粒子的运动受到洛伦兹力和离心力的共同作用。

1. 带电粒子在平行磁场中的运动。

当带电粒子的速度与非均匀磁场的方向平行时，洛伦兹力和离心力共同作用，使得带电粒子的运动轨迹偏离直线，呈现偏转或弯曲的状态。

2. 带电粒子在非均匀磁场中的稳定运动。

在某些特殊的非均匀磁场中，带电粒子可以实现稳定的运动。

例如，带电粒子在磁偶极场中做稳定的进动运动。

四、在磁场中运动的带电粒子与其他力的作用在实际情况中，带电粒子在磁场中的运动常常受到其他力的作用，如重力和电场的作用。

1. 在重力作用下的带电粒子运动。

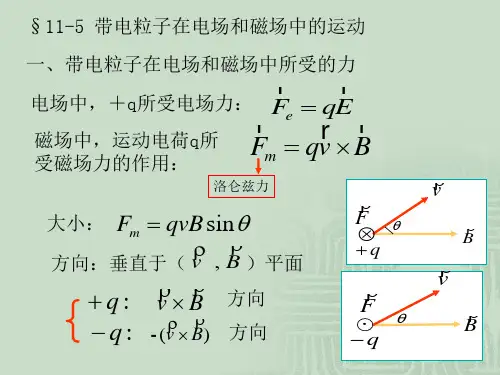
一、带电粒子在电场和磁场中所受的力电场力Eq F =e 磁场力（洛仑兹力）Bq F ×=v m Bq E q F ×+=v 运动电荷在电场和磁场中受的力方向：即以右手四指由经小于的角弯向，拇指的指向就是正电荷所受洛仑兹力的方向.Bv180§11-6 带电粒子在电场和磁场中所受作用及运动141967.4100.151.610 3.110F B T T qv −−×===×××例: 一质子沿着与磁场垂直的方向运动, 在某点它的速率为. 由实验测得这时质子所受的洛仑兹力为.求该点的磁感强度的大小.16s m 101.3−⋅×N 104.714−×解由于与垂直，可得vB 问1）洛仑兹力作不作功？2）负电荷所受的洛仑兹力方向？例：宇宙射线中的一个质子以速率v= 1.0×107m/s 竖直进入地球磁场内，估算作用在这个质子上的磁力有多大？197417sin 1.610 1.0100.310sin904.810F qvB N Nθ−−−==××××××=× 解:在地球赤道附近的地磁场沿水平方向，靠近地面处的磁感应强度约为B= 0.3×10-4T ，已知质子所带电荷量为q =1.6×10-19 C ，按洛仑兹力公式，可算出场强对质子的作用力为这个力约是质子重量(mg=1.6×10-26N）的109倍，因此当讨论微观带电粒子在磁场中的运动时，一般可以忽略重力的影响。

设有一均匀磁场，磁感应强度为，一电荷量为、质量为的粒子，以初速进入磁场中运动。

Bq m 0v（1）如果与相互平行B 0v=F 粒子作匀速直线运动。

（2）如果与垂直B 0vBqv F 0=粒子作匀速圆周运动。

Bv二、带电粒子在磁场中运动BRvmB qv 20=qB mv R 0=qBm v R T ππ220==Bqv F 0=（3）如果与斜交成θ角B 0vq n v 0 Bθcos 00v v x=θsin 00v v n=qBmv R n 0=qBmv T v h xx π200==qBm T π2=粒子作螺旋运动。

磁场对带电粒子的作用力磁场是物质中存在的一种物理场，它对带电粒子产生作用力的现象被称为磁场对带电粒子的作用力。

这一现象在我们的日常生活和科学研究中均具有重要的应用和意义。

本文将介绍磁场对带电粒子的作用力的原理、公式以及相关领域中的应用。

一、磁场对带电粒子的作用力的原理磁场的存在能够对带电粒子产生作用力，这是基于洛伦兹力的作用原理。

洛伦兹力是描述电荷在电磁场中运动时所受到的力的理论，它由电场力和磁场力两部分组成。

当带电粒子穿过一个磁场时，由于磁场对电荷的作用，将产生力的作用使得带电粒子发生偏转。

二、磁场对带电粒子的作用力的公式磁场对带电粒子的作用力由洛伦兹力公式描述，其表达式为：F = q (v × B)其中，F为磁场对带电粒子作用力的大小，q为带电粒子的电量，v 为带电粒子的运动速度，B为磁场的磁感应强度。

作用力的方向由右手定则确定，即将右手的食指指向带电粒子的速度方向，中指指向磁感应强度方向，那么拇指的方向即为磁场对带电粒子作用力的方向。

三、磁场对带电粒子的作用力在实际中的应用1. 磁力传感器磁力传感器是一种能够通过检测磁场对带电粒子的作用力来测量磁场强度的工具。

它广泛应用于导航设备、工业控制以及科学研究中。

通过测量作用在磁场中的带电粒子上的力，磁力传感器可以准确测量磁场的强度和方向。

2. 粒子加速器粒子加速器是一种能够通过不断增加带电粒子的动能来研究粒子的性质和相互作用的科学工具。

它利用磁场对带电粒子的作用力将带电粒子加速到非常高能量，进而进行各种实验和研究。

粒子加速器被广泛应用于核物理、高能物理等领域中。

3. 电动机电动机是利用磁场对带电粒子的作用力产生机械运动的装置。

在电动机中，通过施加电流使得磁场产生，磁场对电流中的导线中的带电粒子产生作用力，从而引起转动。

电动机被广泛应用于交通工具、工业生产和家用电器等领域。

四、总结磁场对带电粒子的作用力是一种重要的物理现象，它基于洛伦兹力原理描述了磁场对电荷的作用。

磁场中的力讲解磁场中的洛伦兹力和磁力定律磁场中的力：洛伦兹力和磁力定律磁场是物理学中重要的一个概念，它是由电流或者磁体产生的。

磁场不仅对物质有吸引或排斥的作用，还能够产生力，其中最常见的力是洛伦兹力和磁力。

本文将对磁场中的洛伦兹力和磁力定律进行讲解。

一、洛伦兹力的定义和公式洛伦兹力是指磁场中带电粒子所受到的力。

当带电粒子在磁场中运动时，它会受到磁场的作用，产生一个垂直于粒子运动方向和磁场方向的力，这就是洛伦兹力。

洛伦兹力的公式如下：F = q(v × B)其中，F表示洛伦兹力的大小，q是带电粒子的电荷量，v是粒子的速度矢量，B是磁场的磁感应强度矢量。

二、磁力定律的介绍和公式磁力定律是磁场中力的基本定律，它表明磁力的大小与所受力物体、磁感应强度和两者之间的夹角有关。

磁力定律的公式如下：F = qvBsinθ其中，F表示磁力的大小，q是带电粒子的电荷量，v是粒子的速度大小，B是磁场的磁感应强度大小，θ是速度和磁感应强度之间的夹角。

三、洛伦兹力和磁力的区别与联系洛伦兹力是磁场中带电粒子所受到的力，而磁力是任何物体在磁场中受到的力。

洛伦兹力和磁力都与带电粒子的电荷量和运动状态有关，但磁力还受到物体质量的影响。

洛伦兹力和磁力的共同点是它们的方向都垂直于磁场方向和粒子运动方向，并且都能对物体产生做功。

四、磁场中的力的应用磁场中的力有着广泛的应用。

其中最典型的应用是在电动机和发电机中，通过磁场中的力实现电能与机械能的转换。

此外，在粒子加速器中，磁场中的洛伦兹力被用来加速带电粒子，使其获得高速。

在医学中，磁场中的力被应用于磁共振成像（MRI），通过对带有磁性荧光剂的物质进行影像检测，来观察人体结构和病变情况。

磁场中的力还被应用于磁悬浮列车、磁浮飞行器等现代交通工具中，提供了更高效、更环保的交通方式。

总结：磁场中的力包括洛伦兹力和磁力。

洛伦兹力是指带电粒子在磁场中所受到的力，而磁力是物体在磁场中受到的力。

磁场中电荷的受力在物理学中，电荷在磁场中会受到一定的力的作用。

这种力被称作洛伦兹力，它是由电荷带电粒子运动产生的磁场和外部磁场相互作用而引起的。

本文将详细探讨磁场中电荷受力的原理和特点。

一、磁场对电荷的影响当一个带电粒子在磁场中运动时，磁场会对电荷施加作用力。

这个作用力的方向与电荷的运动速度和磁场方向有关。

根据左手定则，我们可以确定洛伦兹力的方向。

左手握拳，将拇指指向电荷的运动方向，四指指向磁场方向，那么拇指的方向就是洛伦兹力的方向。

二、电荷在磁场中的运动轨迹根据洛伦兹力的方向，我们可以得到电荷在磁场中运动的轨迹。

对于正电荷，它将被偏转成顺时针方向；而对于负电荷，它将被偏转成逆时针方向。

这是因为正负电荷在磁场中运动产生的磁场方向相反，从而引起力的反向。

因此，电荷在磁场中的运动轨迹将呈现螺旋状。

三、洛伦兹力的大小洛伦兹力的大小与电荷的运动速度、磁场的强度以及电荷的电荷量之间有关。

根据洛伦兹力的表达式可以得知，洛伦兹力随着电荷量和磁场强度的增加而增大，但与运动速度无关。

四、磁场中电荷受力的数学描述我们可以用数学公式来描述磁场中电荷受力的情况。

洛伦兹力的大小可以通过以下公式计算：F = qvBsinθ其中，F表示洛伦兹力的大小，q表示电荷的电荷量，v表示电荷的运动速度，B表示磁场的磁感应强度，θ表示电荷运动方向与磁场方向之间的夹角。

五、实际应用和意义磁场中电荷受力的原理在许多实际应用中起着重要作用。

例如，在电子枪中，电子在磁场中受到的力使其沿着特定的轨道加速运动，从而产生高速电子束；在磁共振成像中，磁场对人体中的原子核施加力，产生共振信号，实现图像的形成。

此外，研究磁场中电荷的受力现象也有助于我们更深入地理解电磁现象和粒子物理学的基本原理。

六、总结在磁场中，电荷会受到洛伦兹力的作用，力的方向与电荷的运动速度和磁场方向有关。

电荷在磁场中的运动轨迹呈螺旋状，洛伦兹力的大小与电荷量和磁场强度有关。

我们可以用数学公式描述磁场中电荷受力的情况。