网格计算技术在大规模CFD计算上的应用

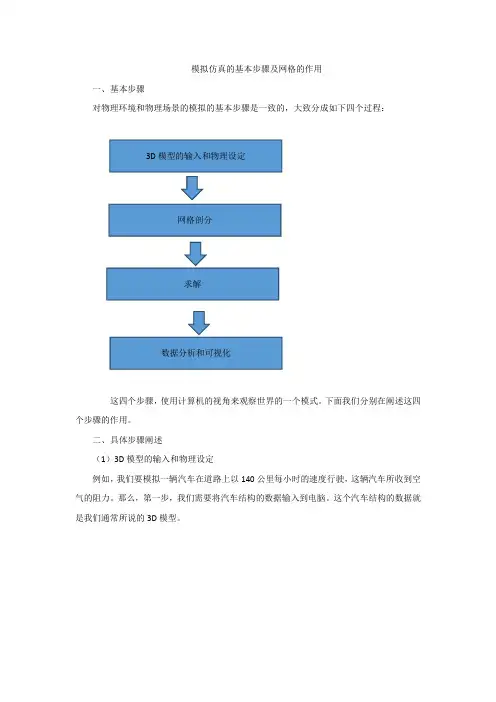
模拟仿真的基本步骤及网格的作用一、基本步骤对物理环境和物理场景的模拟的基本步骤是一致的，大致分成如下四个过程：3D模型的输入和物理设定网格剖分求解数据分析和可视化这四个步骤，使用计算机的视角来观察世界的一个模式。

下面我们分别在阐述这四个步骤的作用。

二、具体步骤阐述（1）3D模型的输入和物理设定例如，我们要模拟一辆汽车在道路上以140公里每小时的速度行驶，这辆汽车所收到空气的阻力。

那么，第一步，我们需要将汽车结构的数据输入到电脑。

这个汽车结构的数据就是我们通常所说的3D模型。

同时，我们还需要给这个汽车一个形式的空间。

通常，由于模拟数据是和风洞试验对比的，我们仍然称这个空间为风洞，只是为了区分，我们称之为数值风洞。

因为它是虚拟的。

风洞的形状通常会是一个方形的。

这样就准备好了我们需要的在结构上的数据。

但是如何和实际的汽车行驶对应起来呢？我们还需要告诉计算机哪个模型是汽车，哪个模型是风洞，他们对应现实中的什么物理特性？例如汽车的轮子是旋转的，汽车的表面会阻碍风的流动等等。

这个步骤称为物理设定。

（2）网格剖分刚才我们已经在计算机里输入了3D模型，并且做了物理属性的设定。

实际上在风洞内包含了风洞的墙，汽车的表面，还有空气。

这些物质的运动是我们需要模拟的。

为了模拟出这些物质的运动，我们需要把这个空间拆分成数千万的小多面体。

每个多面体对应这些物质的一部分，然后进行计算。

将这个空间拆分成数千万小多面体并与物质对应起来的过程，称为网格剖分。

而剖分出来的表征空间和物质的千万个小多面体整体称为网格。

（3）求解有了3D模型，有了物理特性，有了网格剖分，我们就可以建立数学模型实际上是一个方程，进行求解。

这个过程，我们也称为求解。

求解之后，我们就可以获得这个方程的一个解。

这个解，我们可以理解成一个通俗的说法，就是答案。

因为我们希望通过计算的计算来得到汽车在公路上行驶的时候，它的气流分布的答案。

（4）数据分析与可视化经过求解之后，我们获得的答案是一堆数据。

基于网格划分的计算流体力学模拟研究在工程领域，计算流体力学（Computational Fluid Dynamics，简称CFD）已成为一种常见的分析工具，主要用于模拟流体的运动和相应变化，对工程设计和制造等过程进行优化和改进。

在CFD模拟中，网格划分是非常关键的一个环节，它决定了模拟结果的准确性和计算效率。

本文将重点探讨基于网格划分的CFD模拟，并对其研究意义和应用前景进行深入阐述。

1、CFD模拟的基本原理CFD模拟是一种基于数值方法的分析技术，它通过数值模拟来解决流体力学问题。

CFD模拟的基本原理是将流体运动的方程通过数值离散化的方法，转化为一个求解差分方程组的计算问题。

通常采用有限元、有限体积或有限差分等数值方法，将物理问题转化为离散的数值问题。

CFD模拟的基本步骤包括：建立模型、离散化、求解数值方法、结果后处理等。

2、网格划分在CFD模拟中的重要性CFD模拟的计算精度和计算效率都与网格划分有关。

网格划分影响着模拟结果的精度和计算速度，目前工程领域中常用的网格划分方法主要包括结构化网格和非结构化网格两种。

结构化网格是一种规则网格划分方法，具有较高的计算效率和精度，适用于处理简单的几何形状。

非结构化网格则是一种给定形状的无规则网格划分方法，适用于复杂的几何形状。

非结构化网格的精度较高，但计算效率被约束。

根据不同的工程需求和实际问题，选择合适的网格划分方法是为了获得最优的计算精度和计算效率。

3、基于网格划分的CFD模拟研究应用场景在工程领域，CFD模拟广泛应用于飞行器、汽车、船舶、建筑等领域中的气体和流体流动分析。

其中，航空航天领域是CFD模拟的重要应用领域之一，飞行器的气动力学分析、热力学分析和马赫数相关分析等都需要CFD模拟的支持。

另外，在汽车、船舶领域中，CFD模拟也发挥着重要作用，例如汽车外形优化、飞跃撞波的分析等。

4、CFD模拟研究的发展趋势和前景展望随着科技的发展，CFD模拟技术得到了广泛的研究和应用。

CFD 计算对计算网格有特殊的要求，一是考虑到近壁粘性效应采用较密的贴体网格，二是网格的疏密程度与流场参数的变化梯度大体一致。

对于面网格，可以设置平行于给定边的边界层网格，可以指定第二层与第一层的间距比，及总的层数。

对于体网格，也可以设置垂直于壁面方向的边界层，从而可以划分出高质量的贴体网格。

而其它通用的CAE 前处理器主要是根据结构强度分析的需要而设计的，在结构分析中不存在边界层问题，因而采用这种工具生成的网格难以满足CFD 计算要求，而Gambit 软件解决了这个特殊要求。

如果先在一条边上画密网格再在之上画边界层，边界层与网格能很好的对应起来如果直接在一条边上画边界层，则边界层横向之间的距离很宽怎么设置边界层横向之间的距离，即不用先画网格也能画出横向距离很密的边界层来？在划分边界层网格之前，用粘性网格间距计算器，计算出想要的y+值对应的第一层网格高度；第一层高度出来之后，关于网格的纵横向网格间距之比，也就是边界层第一层网格高度与横向间距之比，大概在1/sqrt(Re)，最为适宜；先在你要划边界层网格的边上划分线网格，然后再划分边界层。

gambit本人也用了一段时间，六面体网格四面体网格我都画过，但是最头疼的还是三维边界层网格的生成。

用gambit自带的边界层网格生成功能画出来的边界层网格经常达不到好的效果，或者对于复杂的外形根本就无法生成边界层网格。

为此我就采用手动设置边界层，但是比较费时间，效果还一般。

不知道大家是不是也遇到相似的问题，或者有更好的方法，请指点一下，先谢谢了！22 什么叫松弛因子？松弛因子对计算结果有什么样的影响？它对计算的收敛情况又有什么样的影响？1、亚松驰（Under Relaxation）：所谓亚松驰就是将本层次计算结果与上一层次结果的差值作适当缩减，以避免由于差值过大而引起非线性迭代过程的发散。

用通用变量来写出时，为松驰因子（Relaxati on Factors）。

结构网格CFD应用程序在天河超级计算机上的高效并行与优化IntroductionComputational Fluid Dynamics (CFD) has become an essential tool in modern engineering applications. It involves the numerical simulation of fluid flow and heat transfer through complex geometries based on the Navier-Stokes equations. In recent years, the computing power of High-Performance Computing (HPC) systems has significantly increased, enabling the simulation of complex problems with finer resolutions and greater accuracy. This paper describes the efficient parallelization of a structured grid CFD application on the Tianhe-2 supercomputer, along with optimization techniques to achieve the best performance.Structured Grid CFD ApplicationStructured grid methods are widely used in CFD applications, where the computational domain is divided into a set of regular grid cells. The structured grid provides a uniform resolution throughout the domain, allowing for accurate modeling of the flow and minimizing the numerical error. The CFD application used in this study is a structured grid solver for incompressible Navier-Stokes equations. The numerical method used is a second-order accurate finite volume method on a collocated grid. The equations are solved using an iterative method, such as the SIMPLE algorithm, which involves solving a set of algebraic equations for eachgrid cell.High-Performance Computing on Tianhe-2Tianhe-2 is a supercomputer located in Guangzhou, China, with a peak performance of 54.9 Petaflops. It consists of 16,000 nodes, each with two Intel Xeon Ivy Bridge processors and three Xeon Phi coprocessors. The nodes are interconnected by a high-speed network, allowing for efficient communication between nodes. The Tianhe-2 supercomputer is an ideal platform for large-scale CFD simulations due to its vast computational power.ParallelizationEfficient parallelization is essential for achieving high performance on a supercomputer. The structured grid CFD application has been parallelized using Message Passing Interface (MPI) to exploit parallelism across multiple nodes. Each node is responsible for a subset of the grid cells, and the computation is divided evenly between them. The communication between nodes is handled using the MPI Alltoall collective communication function for exchanging boundary values. Load balancing is critical for efficient parallelization, and an efficient load balancing algorithm is required to achieve optimal performance.Load BalancingThe load balancing algorithm used in this study is the Recursive Coordinate Bisection (RCB) algorithm. It divides the computational domain recursively into two using a set of planes perpendicular to the coordinate axes. The planes are chosen to ensure that the number of grid cells on either side of the plane is roughly equal. This process is repeated until each node is assigned a reasonably balanced subset of thegrid cells. The RCB algorithm is simple to implement and hasbeen shown to provide efficient load balancing for a wide range of applications.Optimization TechniquesSeveral optimization techniques have been used toimprove the performance of the structured grid CFDapplication on Tianhe-2. These optimizations involveminimizing the communication overhead, reducing the computational time, and improving memory utilization.Communication OverheadMinimizing the communication overhead is critical for efficient parallelization. The MPI Alltoall function used for exchanging boundary values involves communication between all nodes and can become a bottleneck for large-scale simulations. To minimize this overhead, a two-level communication strategy has been implemented. The first level involves communication between neighboring nodes using the MPI Send and Receive functions, while the second level involves the MPI Alltoall function for exchanging boundary values between non-neighboring nodes. This two-level communication strategy has been shown to reduce the total communication timesignificantly.Computational TimeReducing the computational time required for eachiteration is crucial to achieving high performance. One optimization technique used in this study is loop unrolling. Loop unrolling involves manually increasing the number of iterations executed in each loop, reducing the number of loop instructions and improving cache utilization. Another optimization technique is temporary Array Elimination. This technique involves eliminating unnecessary temporary arrays used for intermediate calculations, reducing the memoryaccessed during computation and improving cache utilization.Memory UtilizationThe efficient utilization of memory is essential for optimal performance. One optimization technique used in this study is memory alignment. Memory alignment involves aligning data structures to the size of the cache line, allowing for efficient memory access and reducing cache misses. Other techniques include loop blocking and loop tiling, which involve partitioning large loops into smaller ones, reducing the amount of memory accessed during computation and improving cache utilization.ConclusionIn conclusion, the efficient parallelization and optimization of a structured grid CFD application on the Tianhe-2 supercomputer have been described. The software has been parallelized using MPI, and the RCB algorithm has been used for load balancing. Optimization techniques such as loop unrolling, temporary Array Elimination, memory alignment, loop blocking, and loop tiling have been used to achieve the best performance. The optimized software has been tested on various problem sizes and shown to scale well up to 8000 nodes, achieving a parallel efficiency of 83%. The optimizations described in this paper can be applied to other similar CFD applications, allowing for efficient use of supercomputers for large-scale simulations.。

网格计算法在实际测量中的应用1. 引言1.1 介绍网格计算法网格计算法是一种数值分析方法，广泛应用于各种科学领域中。

它通过将研究区域划分为规则的网格单元，然后对每个单元进行计算和求解，从而得到整个区域的数值结果。

这种方法的特点是能够有效地处理复杂的数学模型，同时具有较高的精度和稳定性。

在实际测量领域中，网格计算法可以帮助研究人员快速准确地进行数据处理和分析。

通过将实际测量数据输入到网格计算模型中，可以进行各种复杂的数值运算，从而得到更加准确和可靠的结果。

这种方法不仅可以帮助科研人员快速解决实际测量中遇到的难题，还可以为实际测量领域的发展提供新的思路和方法。

网格计算法在实际测量领域中具有重要的应用价值和广泛的发展前景。

通过不断地改进和完善这种方法，我们可以更好地应对复杂的实际测量问题，促进实际测量技术的进步和发展。

1.2 引入实际测量领域实际测量是现实生活中非常重要的一项工作，它涉及到地质勘探、气象预测、医学影像处理、工程测量等众多领域。

在实际测量中，准确的数据和信息是至关重要的，而网格计算法的应用为实际测量提供了一种高效、精确的计算方法。

通过网格计算法，我们可以更加准确地对实际测量中的复杂数据进行处理和分析，从而得到更加可靠的结果。

在地质勘探中，网格计算法可以帮助我们模拟地下结构，找出潜在的矿藏资源；在气象预测中，可以通过网格计算法对大气环流进行模拟，提高气象预测的准确性；在医学影像处理中，可以利用网格计算法对医学影像进行分析和处理，帮助医生更好地诊断病情；在工程测量中，可以通过网格计算法对建筑物结构进行模拟和分析，确保工程质量。

网格计算法在实际测量中的应用是非常广泛的，它为实际测量提供了一种高效、精确的计算方法，为实际测量工作的开展提供了重要的支持和保障。

展望未来，随着技术的不断进步和发展，网格计算法在测量领域的应用将会越来越广泛，为实际测量工作带来更多的技术创新和发展机遇。

2. 正文2.1 网格计算法原理及特点网格计算法（Grid Computing）是一种基于计算资源共享的计算模式，通过将多个计算资源（包括计算机、存储和网络等）整合在一个虚拟的分布式系统中，实现对大规模数据和复杂计算任务的高效处理。

超大规模结构网格CFD数值模拟的初步研究在科技的海洋中，计算流体动力学（CFD）如同一艘精密的航船，它承载着科学家们对流体世界未知领域的探索梦想。

随着计算机技术的飞速发展，超大规模结构网格CFD数值模拟成为了这一领域中的新星，其光芒逐渐照亮了流体力学的未来。

首先，让我们来探讨一下超大规模结构网格CFD数值模拟的重要性。

在传统的CFD模拟中，由于计算资源的限制，我们往往只能对有限的区域进行模拟，这就像是在茫茫大海中只观察一滴水一样，虽然可以得出一些结论，但总是缺乏全局的视角。

而超大规模结构网格的出现，就像是给我们配备了一副望远镜，使得我们可以从更广阔的角度去观察和理解流体的行为。

然而，超大规模结构网格CFD数值模拟并非没有挑战。

它的计算量巨大，对计算机的性能要求极高，这就像是驾驶一艘巨轮穿越汹涌的海浪，需要有足够的动力和稳定性才能确保航行的安全。

此外，随着网格数量的增加，数值误差也会累积，这就需要我们像精密的钟表匠一样，对每一个细节都进行精确的调整和控制。

在实际应用中，超大规模结构网格CFD数值模拟已经展现出了其强大的能力。

在航空航天领域，它可以帮助我们更准确地预测飞行器周围的气流分布；在气候变化研究中，它可以模拟全球范围内的气候系统；在能源开发中，它可以优化风力发电机的设计。

这些应用就像是一颗颗璀璨的明珠，镶嵌在科技发展的皇冠上。

但是，我们也必须看到，超大规模结构网格CFD数值模拟还处于初级阶段，它的潜力还远远没有被完全挖掘出来。

我们需要更多的研究来提高其精度和效率，需要更多的创新来解决目前存在的问题。

这就像是一场马拉松比赛，我们现在只是刚刚起步，前方的道路还很长。

在未来的发展中，超大规模结构网格CFD数值模拟将会与人工智能、大数据等技术紧密结合，形成更为强大的工具。

它将会在更多的领域发挥作用，比如在环境保护、生物医学、材料科学等方面，都将有其独特的贡献。

这就像是一场科技的革命，将会改变我们对世界的认知和利用方式。

大规模多区结构网格CFD应用的高效并行模拟技术王勇献1*, 张理论1, 刘巍1, 车永刚1, 徐传福1, 王正华1(1 国防科学技术大学计算机学院, 湖南长沙410073)摘要本文就多区结构网格上的大规模CFD流场模拟的高效并行方法进行了研究，并讨论了在天河超级计算机上与运行时相关的性能提升措施，测试结果表明该并行实现可获得了较大的性能提升。

关键词计算流体力学; 多区结构网格; 并行计算; MPI+OpenMP; CPU核绑定1 引言近年来，随着计算流体力学（CFD）方法的不断突破和计算机技术的快速发展，基于CFD 的数值模拟方法开始越来越多地被应用到航空航天飞行器的研究和设计当中，成为航空航天飞行器研制的有力工具。

为了提高CFD数值模拟的计算规模、计算效率，更好地满足工程设计、科学研究等目标，CFD数值模拟代码通常需要并行计算，以便充分利用高性能计算机的强大并行处理能力。

CFD数值模拟代码的计算核心是求解器，其中包括CFD的模型离散、计算格式等。

CFD程序读入由前处理产生的网格数据后，根据给定的流场初始条件进行初始化，最终通过求解器对流动方程获得流场变量的数值模拟结果。

CFD求解器通常是整个程序中计算量最大最为耗时的部分，其并行实现直接影响了CFD程序的整体性能，是CFD并行研究的主要对象。

传统的并行CFD程序采用区域分解方式，根据高性能计算机特点，可以实现为共享存储或消息传递并行程序，不同区域在不同进程或线程上运行求解器，获得每个时间步的流场结果后需要对区域之间的边界进行信息交换。

在利用CFD进行大规模流场的并行数值计算过程中，需要综合考虑CFD应用特点和高性能计算机体系结构，以获得最佳的模拟性能。

除了传统并行数值模拟应用中的负载平衡、任务分配等因素外，本文试图从优化配置并行应用的运行时环境这一视角出发，探索CFD应用软件与高性能计算平台的最优适配策略，同时考虑超大问题规模并行数值计算中的容错等新问题，研究相应解决方案，最终实现大规模多区结构网格CFD应用的高效并行数值模拟。

近地湍流风场的CFD模拟研究一、概述近地湍流风场作为大气边界层的重要特征之一，对飞行器的安全起降、风电场的能量捕获效率以及建筑结构的风荷载分析等方面都具有至关重要的影响。

对近地湍流风场的准确模拟和深入研究，不仅有助于提升相关工程领域的设计水平，也是气象学和流体力学等学科领域的重要研究课题。

随着计算机技术的快速发展，计算流体动力学（CFD）作为一种强大的数值模拟工具，已广泛应用于湍流风场的模拟研究中。

通过构建复杂的数学模型和算法，CFD能够模拟出湍流风场的精细结构和动态演变过程，从而为风工程领域的实际应用提供有力的理论支撑。

近地湍流风场的CFD模拟研究仍面临诸多挑战。

湍流本身具有高度的复杂性和不确定性，其生成、发展和传播过程受到多种因素的影响，如地形、地表粗糙度、大气稳定度等。

如何准确地描述和模拟这些影响因素对湍流风场的影响，是CFD模拟研究的关键问题之一。

近地湍流风场的模拟通常需要处理大规模的网格和复杂的边界条件，这对计算资源和算法效率提出了更高的要求。

如何在保证模拟精度的降低计算成本和提高计算效率，也是CFD模拟研究需要解决的重要问题。

随着风工程领域的不断发展，对近地湍流风场模拟的精度和可靠性要求也在不断提高。

不断探索和创新CFD模拟方法和技术，以适应不同应用场景的需求，也是当前和未来研究的重要方向。

近地湍流风场的CFD模拟研究具有重要的理论价值和实际应用意义。

通过深入研究湍流风场的生成机制和演变规律，不断优化和完善模拟方法和技术，将为风工程领域的发展提供有力的支持。

1. 近地湍流风场的研究背景与意义近地湍流风场的研究在现代气象学、风能利用以及环境科学等领域具有举足轻重的地位。

近地面风速受到地表摩擦、地形起伏、建筑物以及其他障碍物等多种因素的影响，呈现出显著的非均匀性和复杂性。

这种复杂性使得近地湍流风场的准确预测和模拟变得尤为困难，但同时也为相关领域的研究和应用提供了广阔的探索空间。

在风能利用方面，近地湍流风场的研究对于提高风能转换效率和风机设计优化具有至关重要的作用。

一些需要了解的关于CFD的常识关于网格：1. 网格是CFD 的几何表达形式，也是模拟和分析的载体。

2. 网格质量对CFD 计算的精度和效率影响很大。

3. 单连域：求解区域边界线内不包含有非求解区域。

多连域：求解区域含有非求解区域。

4. 绕流问题的网格一般为O 型和C 型网格。

考虑使用结构还是非结构网格的时候，主要考虑以下几个因素：1. 主要考虑网格的多少，这才是真正影响计算消耗最大的因素。

主要从以下的观点进行考虑。

当几何外形太复杂或者流动的长度尺度太大时，三角形网格和四面体网格所生成的单元会比等量的包含四边形网格和六面体网格的单元少得多。

这是因为三角形网格和四面体网格允许单元聚集在流域的所选区域，而四边形网格和六面体网格会在不需要加密的地方产生单元。

非结构的四边形网格和六面体网格为对于一般复杂外形提供了许多三角形和四面体网格的优点。

（复杂外形建议用非结构网格）2. 网格的比率。

四边形和六边形单元的一个特点就是它们在某些情况下可以允许比三角形/四面体单元更大的比率。

三角形/四面体单元的大比率总会影响单元的歪斜。

因此，如果你有相对简单的几何外形，而且流动和几何外形很符合，比如长管，你就可以使用大比率的四边形和六边形单元。

这种网格可能会比三角形/四面体网格少很多单元。

（流动和外形比较符合且外形简单时，建议使用结构网格）关于数值耗散问题，有如下几点：● 当真实耗散很小时，即对流占主导地位时，数值耗散是显而易见的。

● 所有的解决流体问题的数值格式都会有数值耗散，这是因为数值耗散来源于截断误差，截断误差是描述流体流动的离散方程导致的。

●FLUENT 中所用的二阶离散格式可以帮助减少解的数值耗散的影响。

● 数值耗散量的大小与网格的分辨率成反比。

因此解决数值耗散问题的一个方法就是精化网格。

● 当流动和网格成一条直线时数值耗散最小（所以我们才要使用结构网格来计算啊）最后一点和网格选择最有关系。

很明显，使用三角形/四面体网格流动永远不会和网格成一条直线，而如果几何外形不是很复杂时，四边形网格和六面体网格可能就会实现流动和网格成一条线。

自适应网格技术在计算流体力学中的应用计算流体力学（Computational Fluid Dynamics，简称CFD）是一门研究流体力学问题的科学和工程技术方法。

它通过数值方法对流体力学方程进行离散化，并利用计算机模拟流体力学问题的运动和相互作用。

而自适应网格技术作为计算流体力学的重要工具之一，可以对流体流动区域进行细分和调整，以获得更精确的仿真结果。

自适应网格技术通过根据流体流动的特性和计算需要，动态地调整计算网格的分辨率，以达到更好的数值计算精度和效率。

在计算流体力学的应用中，自适应网格技术主要有以下几个方面的应用。

首先，自适应网格技术可以提高计算的精度。

在流体力学仿真中，流场往往存在着复杂的流动结构和梯度变化，传统的均匀网格很难完全捕捉到这些细节。

通过自适应网格技术，可以根据流场中的梯度变化情况，对流动的关键区域进行细化，并加密网格，以提高数值计算的精度。

其次，自适应网格技术可以提高计算的效率。

在仿真大规模流动问题时，计算网格的密度会影响计算的时间和空间复杂度。

通过自适应网格技术，可以根据流场的特性，灵活调整网格的密度，从而减小计算量，提高仿真的效率。

另外，自适应网格技术可以处理流动问题中的局部异常区域。

在某些情况下，流动的关键区域可能会有局部的异常，例如激波或涡旋。

针对这些异常区域，通过自适应网格技术可以对其进行网格细化，以获得更精确的流场分布和数值计算结果。

自适应网格技术的应用不仅仅局限于二维流场，在三维流体力学仿真中同样发挥着重要的作用。

对于三维流场，自适应网格技术可以在不同方向上进行细化，以更好地捕捉流动的细节和变化。

总体而言，自适应网格技术在计算流体力学中的应用对于提高数值计算的精度和效率，以及处理流动问题中的异常区域具有重要的意义。

它能够根据流体流动的特性，在计算中动态地调整网格的分辨率，以达到最佳的数值计算结果。

随着计算能力的不断提升和自适应网格技术的发展，相信它在计算流体力学领域的应用会得到更多的发展和推广。

文章编号: (2009)-22气动院航空并行CFD计算平台及应用王志川 董军 张铁军 王娜(中国航空工业空气动力研究院 沈阳 110034)摘要中航工业空气动力研究院航空高精度并行CFD平台，目的是开发并验证能满足工业设计所要求的高可靠和高有效性的数值计算工具，用于大型客机（运输机）全机粘性流场空气动力模拟和气动设计。

航空并行CFD平台软件系统包括分区多块结构网格（嵌套网格）并行CFD计算子系统和非结构混合网格并行CFD计算子系统。

本文简要介绍了航空并行CFD计算平台，并通过采用AIAA阻力评估组给出的标准机翼和民机DLR-F6标模的验证计算，获得了比较满意的计算结果和收敛效果。

航空并行CFD平台为大型客机设计提供了计算工具，将在大型客机及运输机的气动设计方面发挥重要作用。

关键词计算流体动力学空气动力并行计算民机1 引言计算机软硬件技术和计算流体力学(CFD) 的高速发展使得CFD技术在航空飞行器设计工作中越来越占据了重要的位置，飞机型号的布局选型、初步和详细设计阶段往往需要通过大量的CFD计算来完成，而风洞试验也需要CFD计算来指引试验方向和对试验结果进行有效修正，在雷诺数修正、布局优化设计、详细流场刻画等方面,CFD较风洞试验更具有优势。

因此，依靠航空CFD数值模拟技术，既便于分析各种流动参数对流动规律的影响，又能快速对设计方案进行评估和优化，还可以指导后继的风洞试验验证工作，避免盲目性造成的设计过程反复，从而达到提高设计质量、缩短研制周期和降低研制成本。

在大型客机气动设计过程中，世界各个客机设计与制造商均在综合利用先进的CFD工具、风洞实验技术以及飞行试验技术，节约研制成本、缩短研制周期，同时提高飞机升阻比和巡航效率，以期获得良好的经济效益。

波音公司在高性能计算报告中指出，1980年波音在风洞中测试了77种模型，最终得出了767的机翼设计方案。

仅仅25年后，通过使用CFD工具，波音制作并测试了11种787机翼，降低了超过80%的试验。

网格计算法在实际测量中的应用导言网格计算法是一种常用的数据处理和计算方法，它可以帮助我们对复杂的实际测量数据进行分析和处理，得到准确的结果。

在实际测量中，网格计算法被广泛应用于地理信息系统、气象学、环境科学、地质勘探等领域，为科研和实践工作提供了重要支持。

本文将介绍网格计算法的基本原理和特点，以及其在实际测量中的应用案例，希望能够帮助读者更好地理解和运用这一方法。

一、网格计算法的基本原理和特点1. 基本原理网格计算法是一种将空间数据离散化的方法，它将给定的空间区域分割成有序的网格单元，然后在每个网格单元内进行数据处理和计算。

通常情况下，网格计算法会将空间区域按照一定的间隔进行分割，形成一个由网格单元组成的网格系统。

在实际测量中，我们可以利用网格计算法对地表的高程、温度、湿度、污染物浓度等进行插值和预测，从而得到空间分布规律和趋势。

2. 特点网格计算法具有以下几个特点：（1）空间离散化：网格计算法将空间区域进行离散化处理，使得原始数据可以被有效地表示和处理。

（2）数据插值：网格计算法可以将离散化的空间数据进行插值，并在网格单元中进行计算，得到相对准确的预测结果。

（3）高效性：由于网格计算法采用离散化的处理方式，可以极大地提高数据处理和计算的效率，特别是对于大规模的空间数据。

（4）适用性广泛：网格计算法适用于各种类型的空间数据，并且在地理信息系统、气象预测、环境监测等领域有着广泛的应用。

1. 地表高程插值地表高程是地理信息系统中的重要数据之一，它对于土地利用规划、道路建设、水资源管理等方面有着重要的作用。

在实际测量中，我们可以利用网格计算法对地表高程进行插值，从而得到高程的空间分布规律和趋势。

在一些山地地区，由于地形复杂和观测点的限制，我们很难获得准确的高程数据。

利用网格计算法，我们可以将观测点数据进行插值，得到整个山地地区的高程分布情况，为相关规划和管理提供重要参考。

2. 气象数据预测气象学是一个典型的空间数据处理和预测领域，而网格计算法在气象数据处理中有着广泛的应用。

基于网格计算的高性能计算应用研究高性能计算是现代科学和工程领域中不可或缺的一部分，随着计算机硬件技术和软件技术的不断发展，高性能计算的应用场景与方式也在逐步扩展与升级。

而针对大规模数据处理和计算需求，基于网格计算的高性能计算应用也逐渐崭露头角。

本文将从基本概念、应用场景、实现方式和发展趋势等方面进行分析探讨。

一、基本概念网格计算(Grid Computing)是指将具有独立管理的计算机、网络、存储和数据资源，通过 Internet 建立虚拟的供应链条或组织结构，进行数据共享和协同处理的技术体系。

它是一种新的分布式计算模式。

在网格计算模式下，用户可以在任意地点通过计算网格来获取到其需要的计算能力、数据和文档等资源。

相较于更传统的集中式计算模式，网格计算具有更高效、更灵活、更可靠、更安全的特点。

二、应用场景网格计算是一种高端、复杂的分布式计算和数据共享形式，主要适用于以下数据处理和计算场景：1. 大规模计算和数据密集型应用：如传统的科学计算、气象预测、大数据分析等。

2. 分散的、异构的数据源和处理资源利用：如跨互联网合作、跨组织、跨界科学计算等。

3. 海量数据存储和管理：如超级数据中心、大型数据仓库等。

三、实现方式网格计算的实现需要依靠一系列的技术支持和基础设施。

下面是网格计算的主要实现方式：1. 网格中间件：底层的网格基础设施，用于构建具有高度可靠性、强大能力、易用性和扩展性的分布式计算环境。

常见的网格中间件包括：Globus Toolkit、Sun Grid Engine、IBM Tivoli等。

2. 资源管理器：用于管理分布式的硬件、软件和数据资源，并进行调度和协同。

3. 安全机制：授权和管理对资源的访问和使用，保证数据隐私和安全。

4. 应用程序接口(API)：提供易用和标准的接口和软件开发工具，便于应用程序的设计和开发。

四、发展趋势网格计算技术是目前分布式处理技术领域的重要研究领域之一，未来的网格计算趋势具有以下几个方向：1. 更加安全和隐私的分布式处理：更多的安全控制和规则，以确保数据的隐私性。

1009 CFD基础和网格计算I0、计算流体力学（CFD）基础计算流体动力学（Computational Fluid Dynamics, CFD）是近代流体力学、数值数学和计算机科学相结合的产物，是一门具有强大生命力的边缘科学。

CFD方法是对流场的控制方程用计算数学的方法将其离散到一系列网格节点上求其离散的数值解的一种方法。

控制所有流体流动的基本定律是：质量守恒定律、动量守恒定律和能量守恒定律。

由它们分别导出连续性方程、动量方程（N-S方程）和能量方程。

应用CFD方法进行平台内部空气流场模拟计算时，首先需要选择或者建立过程的基本方程和理论模型，依据的基本原理是流体力学、热力学、传热传质等平衡或守恒定律。

由基本原理出发可以建立质量、动量、能量、湍流特性等守恒方程组，如连续性方程、扩散方程等。

这些方程构成非线性偏微分方程组，不能用经典的解析法，只能用数值方法求解。

求解上述方程必须首先给定模型的几何形状和尺寸，确定计算区域并给出恰当的进出口、壁面以及自由面的边界条件。

而且还需要适宜的数学模型及包括相应的初值在内的过程方程的完整数学描述。

求解的数值方法主要有有限差分法（FDM）、有限元法（FEM）以及有限分析法（FAM），应用这些方法可以将计算域离散为一系列的网格并建立离散方程组，离散方程的求解是由一组给定的猜测值出发迭代推进，直至满足收敛标准。

常用的迭代方法有Gauss-Seidel迭代法、TDMA方法、SIP法及LSORC法等。

利用上述差分方程及求解方法即可以编写计算程序或选用现有的软件实施过程的CFD模拟。

1、CFD求解力学问题的过程2、网格计算网格，即在计算区域内一些列离散的点。

计算流体力学通过将控制方程离散，使用数值方法得到网格节点上的数据（如速度、温度、压力等），即数值解。

控制方程的离散方法主要由有限控制体积法、有限差分方法和有限元方法。

网格主要分为结构化网格和非结构化网格。

结构化网格，可以用一个固定的法则予以命名，非结构化网格的节点位置不能用一个固定的法则予以有序的命名。

第27卷　第6期空气动力学学报Vol.27,No.6 2009年12月ACTA AER ODYNAMICA SINICA Dec.,2009　文章编号:025821825(2009)0620696205网格计算技术在大规模CFD计算上的应用蔡巧言1,杜　涛2(1.西北工业大学航空学院,西安　710072;2.中国运载火箭技术研究院研究发展中心,北京　100076)摘　要:针对大规模数值计算规模化管理的难题,采用网格计算技术将网络环境下分散的计算资源组建了CFD网格计算环境。

采用主动接入方式,以中心服务器为核心的网格计算管理和服务模式,构建CFD网格计算环境,实现了CFD计算在网格环境内的自动化计算管理,提高了计算资源的利用效率,降低了设计人员的劳动强度。

关键词:网格计算;CFD;大规模计算中图分类号:V211.3 文献标识码:A0　引　言 随着CFD技术的日益成熟,计算能力的高速增长,计算资源的成本快速降低,CFD计算技术在现代飞行器的气动设计中能够发挥越来越大和越来越深刻的作用[1]。

目前,所面临的最大问题不再是计算资源的不足,而是如何利用好、管理好庞大的计算资源,发挥出高性能计算资源应有的作用。

两个突出的瓶颈问题是网格生成技术和计算过程的管理和调度仍然处于手工状态,已经不适应CFD大规模化的需求,阻碍了CFD技术在工程设计上的应用[2]。

如果不重视和解决这些问题,计算资源的高速增长并不会必然带来CFD计算质量和计算效率的双重提高。

美国是世界上信息资源最发达的国家,NASA 很早就面临大规模计算引入工业设计系统的障碍。

为此,NASA在2001年开展了CICT计划,其目的就是确保NASA在融合数字技术方面继续保持领先地位。

其中的CN IS(Comp uting,Networking and In2 formation Systems)子计划的核心就是试图将地面、空中和太空中的各种分布式信息资源整合在一起, CFD计算人员能够方便地进入和利用这些信息资源,同时资源对工程科研人员又是透明的。

我所知道的计算流体力学大牛们计算流体力学（CFD）是一门涉及数学、物理学和计算机科学的交叉学科，广泛应用于工程和科学领域。

下面是一些在CFD领域做出重要贡献的大牛们。

1. Jameson, Antony：Jameson教授是CFD领域的先驱之一，他提出了著名的领先-追赶格式方法，用于解决非稳态问题。

他还开发了自适应网格技术，用于提高CFD计算的精度和效率。

2. Anderson, John D. Jr.：Anderson教授是航空航天工程和计算流体力学领域的一位重要学者。

他在CFD中的突出贡献包括开发了NASA 的三维多块结构网格生成软件。

他还合著了《计算流体力学和有限元法》等经典著作。

3. Roache, Patrick J.：Roache教授被誉为CFD方法验证和验证的权威。

他提出了CFD验证的概念，并开发了一系列方法和标准，以确保CFD计算的准确性和可信度。

他的贡献促进了CFD方法的发展和应用。

4. Chorin, Alexandre Joel：Chorin教授提出了著名的分数阶步进方法（Fractional Step Method），用于解决不可压缩流动的Navier-Stokes方程。

这种方法极大地简化了CFD计算的过程，并被广泛应用于工程实践中。

5. Melnik, Roderick V. N.：Melnik教授在CFD领域做出了重要贡献，特别是在多孔介质流动和多孔介质材料的数值模拟方面。

他开发了多孔介质流动的理论模型和数值方法，并应用于地球物理、生物医学和工程等领域。

6. Ferziger, Joel H.：Ferziger教授是CFD领域的重要学者之一，他合著了《计算流体力学》这本广泛使用的教材。

他的研究涵盖了流体力学的各个方面，包括湍流模拟、边界条件处理和数值方法的改进等。

7. Peric, Milovan：Peric教授在CFD的边界条件处理和有限体积方法方面做出了重要贡献。