高二数学天天练(59)

高二数学天天练（101） 姓 名 得 分1、若i xyi y x 152)(+-=-+，则y x ,分别为2、若i m m m m z )242()43(22--+-+=是纯虚数，则m =3、=+++)3)(2)(1(i i i4、若1)43(=-+i z ，则=z5、若,1i z +=且2)2(2z a z b az +=+，则b a ,分别为月 日高二数学天天练（101） 姓 名 得 分1、若i xyi y x 152)(+-=-+，则y x ,分别为2、若i m m m m z )242()43(22--+-+=是纯虚数，则m =3、=+++)3)(2)(1(i i i4、若1)43(=-+i z ，则=z5、若,1i z +=且2)2(2z a z b az +=+，则b a ,分别为月 日高二数学天天练（102） 姓 名 得 分1、=+10)1(i2、ii i i 34)2(43)21(22-++++=3、若yi x ii +=++-32111，则y x ,分别为 4、若i z 2472--=，则=z 5、若,11i z +=且113z z z z +=⋅，则=z月 日高二数学天天练（102） 姓 名 得 分1、=+10)1(i2、ii i i 34)2(43)21(22-++++=3、若yi x ii +=++-32111，则y x ,分别为 4、若i z 2472--=，则=z 5、若,11i z +=且113z z z z +=⋅，则=z月 日高二数学天天练（103） 姓 名 得 分1、=-|1|ii2、若i z -=1，则=||3z3、若复数)2)(1(i bi ++是纯虚数，则=b4、若i m z i z -=+=21,32且21z z 是实数，则=m 5、若,5)1|(|i z z +-=则=z月 日高二数学天天练（103） 姓 名 得 分1、=-|1|ii2、若i z -=1，则=||3z3、若复数)2)(1(i bi ++是纯虚数，则=b4、若i m z i z -=+=21,32且21z z 是实数，则=m 5、若,5)1|(|i z z +-=则=z月 日高二数学天天练（104） 姓 名 得 分1、三点)2,4(),1,5(),2,(m m -共线，则m =2、0=a 是)()(2R x ax x x f ∈+=为偶函数的 条件3、15,1==c b 焦点在y 轴上的椭圆标准方程为4、x ⊥-=-=),,2,4(),3,1,2(，则=x5、已知抛物线y ＝ax 2＋bx －5在点(2,1)处的切线为y ＝－3x ＋7，则a ＝ ，b ＝ .月 日高二数学天天练（104） 姓 名 得 分1、三点)2,4(),1,5(),2,(m m -共线，则m =2、0=a 是)()(2R x ax x x f ∈+=为偶函数的 条件3、15,1==c b 焦点在y 轴上的椭圆标准方程为4、x ⊥-=-=),,2,4(),3,1,2(，则=x5、已知抛物线y ＝ax 2＋bx －5在点(2,1)处的切线为y ＝－3x ＋7，则a ＝ ，b ＝ .月 日高二数学天天练（105） 姓 名 得 分1、直线02)32()2(2=---++m y m m x m 在x 轴上截距为3，则m 为2、N M >是N M 22log log >的 条件3、椭圆11271622=+y x 的焦点坐标为4、若4),2,2,1(),10,5,0(2=⋅--=-=+c a c b a ，则=⋅5、已知直线y ＝kx ＋1与曲线y ＝x 3＋ax ＋b 切于点(1,3)，则b 的值为月 日高二数学天天练（105） 姓 名 得 分1、直线02)32()2(2=---++m y m m x m 在x 轴上截距为3，则m 为2、N M >是N M 22log log >的 条件3、椭圆11271622=+y x 的焦点坐标为4、若4),2,2,1(),10,5,0(2=⋅--=-=+c a c b a ，则=⋅5、已知直线y ＝kx ＋1与曲线y ＝x 3＋ax ＋b 切于点(1,3)，则b 的值为月 日高二数学天天练（106） 姓 名 得 分1、过点)3,4(-在x ，y 轴上截距相等的直线方程的一般式为2、1,->∈∀+x x R x 的否定为3、椭圆13610022=+y x 上点P 到左焦点距离为7，则到右焦点距离为 4、若︒>=<==60,,1||||，则=+|3| 5、函数y ＝12x 2－ln x 的单调减区间为月 日高二数学天天练（106） 姓 名 得 分1、过点)3,4(-在x ，y 轴上截距相等的直线方程的一般式为2、1,->∈∀+x x R x 的否定为3、椭圆13610022=+y x 上点P 到左焦点距离为7，则到右焦点距离为 4、若︒>=<==60,,1||||b a b a ，则=+|3|b a5、函数y ＝12x 2－ln x 的单调减区间为月 日高二数学天天练（107） 姓 名 得 分1、两直线012,01)13(=-+=---my x my x m 垂直，则m 为2、1,->∈∀+x x R x 的否定为3、与椭圆1222=+y x 有相同焦点且过点)23,1(的椭圆标准方程为4、点),3,3(),2,4,1(),1,5,2(n m C B A -+-----共线，则=+n m5、已知f (x )＝(x 2＋x )(x －1)，则=)2('f月 日高二数学天天练（107） 姓 名 得 分1、两直线012,01)13(=-+=---my x my x m 垂直，则m 为2、1,->∈∀+x x R x 的否定为3、与椭圆1222=+y x 有相同焦点且过点)23,1(的椭圆标准方程为4、点),3,3(),2,4,1(),1,5,2(n m C B A -+-----共线，则=+n m5、已知f (x )＝(x 2＋x )(x －1)，则=)2('f月 日高二数学天天练（108） 姓 名 得 分1、过点)2,3(与直线024=-+y x 平行的直线方程为2、“菱形的对角线相互垂直”的否定为3、方程12122=-+-my m x 表示焦点在y 轴上的椭圆，则m 的范围为 4、设n m n m //),23,12,4(),2,32,2(-+=+-=，则n m ,分别为 5、若函数y ＝－x 3＋6x 2＋m 的极大值等于13，则实数m 等于月 日高二数学天天练（108） 姓 名 得 分1、过点)2,3(与直线024=-+y x 平行的直线方程为2、“菱形的对角线相互垂直”的否定为3、方程12122=-+-my m x 表示焦点在y 轴上的椭圆，则m 的范围为4、设n m n m //),23,12,4(),2,32,2(-+=+-=，则n m ,分别为5、若函数y ＝－x 3＋6x 2＋m 的极大值等于13，则实数m 等于月 日高二数学天天练（109） 姓 名 得 分1．给出命题：“若x 2＋y 2＝0，则x ＝y ＝0”，在它的逆命题、否命题、逆否命题中，真命题的个数是______________________________________________________． 2．命题p ：有的三角形是等边三角形．命题非p ：______________________________.3．“x >2”是“1x <12”的____________条件．4．设集合A ＝{x ∈R |x －2>0}，B ＝{x ∈R |x <0}，C ＝{x ∈R |x (x －2)>0}，则“x ∈A ∪B ”是“x ∈C ”的________条件．5．已知α，β的终边在第一象限，则“α>β”是“sin α>sin β”的________________条件.月 日高二数学天天练（109） 姓 名 得 分1．给出命题：“若x 2＋y 2＝0，则x ＝y ＝0”，在它的逆命题、否命题、逆否命题中，真命题的个数是______________________________________________________． 2．命题p ：有的三角形是等边三角形．命题非p ：______________________________.3．“x >2”是“1x <12”的____________条件．4．设集合A ＝{x ∈R |x －2>0}，B ＝{x ∈R |x <0}，C ＝{x ∈R |x (x －2)>0}，则“x ∈A ∪B ”是“x ∈C ”的________条件．5．已知α，β的终边在第一象限，则“α>β”是“sin α>sin β”的________________条件.月 日高二数学天天练（110） 姓 名 得 分1．若命题“∃x ∈R ，有x 2－mx －m <0”是假命题，则实数m 的取值范围是________．2．“a >0且b >0”是“b a ＋ab ≥2”成立的____________条件．3．命题“若m >0，则方程x 2＋x －m ＝0有实根”的逆否命题为____________________． 4．已知命题p ：∃n ∈N,2n >1 000，则非p 为________________．5．函数f (x )＝e x －x 在区间(－∞，0)内是单调__________(填“增函数”或“减函数”)月 日高二数学天天练（110） 姓 名 得 分1．若命题“∃x ∈R ，有x 2－mx －m <0”是假命题，则实数m 的取值范围是________．2．“a >0且b >0”是“b a ＋ab≥2”成立的____________条件．3．命题“若m >0，则方程x 2＋x －m ＝0有实根”的逆否命题为____________________． 4．已知命题p ：∃n ∈N,2n >1 000，则非p 为________________．5．函数f (x )＝e x －x 在区间(－∞，0)内是单调__________(填“增函数”或“减函数”)月 日高二数学天天练（111） 姓 名 得 分1． f ′(x )是函数f (x )＝13x 3＋2x ＋1的导函数，则f ′(－1)的值为________．2．函数f (x )＝x 3＋ax －2在(1，＋∞)上是增函数，则实数a 的取值范围是________． 3．已知f (x )＝x 2＋3xf ′(2)，则f ′(2)＝________.4．已知点P 在曲线f (x )＝x 4－x 上，曲线在点P 处的切线平行于3x －y ＝0，则点P 的坐标为________．5．已知曲线y ＝14x 2－3ln x 的一条切线的斜率为－12，则切点的横坐标为________.月 日高二数学天天练（111） 姓 名 得 分1． f ′(x )是函数f (x )＝13x 3＋2x ＋1的导函数，则f ′(－1)的值为________．2．函数f (x )＝x 3＋ax －2在(1，＋∞)上是增函数，则实数a 的取值范围是________．3．已知f (x )＝x 2＋3xf ′(2)，则f ′(2)＝________.4．已知点P 在曲线f (x )＝x 4－x 上，曲线在点P 处的切线平行于3x －y ＝0，则点P 的坐标为________．5．已知曲线y ＝14x 2－3ln x 的一条切线的斜率为－12，则切点的横坐标为________.月 日高二数学天天练（112） 姓 名 得 分1． f (x )＝3x －x 3的单调减区间为__________．2．设a ∈R ，若函数y ＝e x ＋ax ，x ∈R 有大于零的极值点，则a 的取值范围是__________. 3．函数f (x )＝ax 3＋x 恰有三个单调区间，则a 的取值范围是__________． 4．若函数f (x )＝x ＋a sin x 在R 上递增，则实数a 的取值范围为________．5．已知某生产厂家的年利润y (单位：万元)与年产量x (单位：万件)的函数关系式为y ＝－13x 3＋81x －234，则使该生产厂家获取最大年利润的年产量为________万件．月 日高二数学天天练（112） 姓 名 得 分1． f (x )＝3x －x 3的单调减区间为__________．2．设a ∈R ，若函数y ＝e x ＋ax ，x ∈R 有大于零的极值点，则a 的取值范围是__________.3．函数f (x )＝ax 3＋x 恰有三个单调区间，则a 的取值范围是__________． 4．若函数f (x )＝x ＋a sin x 在R 上递增，则实数a 的取值范围为________．5．已知某生产厂家的年利润y (单位：万元)与年产量x (单位：万件)的函数关系式为y ＝－13x 3＋81x －234，则使该生产厂家获取最大年利润的年产量为________万件．月 日高二数学天天练（113） 姓 名 得 分1.如果圆锥的侧面展开图是半圆，那么这个圆锥的顶角(轴截面中两母线的夹角)是______.2.所有棱长为1的正三棱锥的全面积为________.3.给出三个命题，其中不正确命题的序号是________.①若两条直线和第三条直线所成的角相等，则这两条直线平行； ②若两条直线与第三条直线垂直，则这两条直线互相平行； ③若两条直线与第三条直线平行，这两条直线互相平行； ④若两条直线均与一个平面平行，则这两条直线互相平行.4.表面积为3π的圆锥，它的侧面展开图是一个半圆，则该圆锥的底面直径为________.5.圆台上、下底面面积分别是π、4π，侧面积是6π，这个圆台的体积是______月 日高二数学天天练（113） 姓 名 得 分1.如果圆锥的侧面展开图是半圆，那么这个圆锥的顶角(轴截面中两母线的夹角)是______.2.所有棱长为1的正三棱锥的全面积为________.3.给出三个命题，其中不正确命题的序号是________.①若两条直线和第三条直线所成的角相等，则这两条直线平行；②若两条直线与第三条直线垂直，则这两条直线互相平行；③若两条直线与第三条直线平行，这两条直线互相平行；④若两条直线均与一个平面平行，则这两条直线互相平行.4.表面积为3π的圆锥，它的侧面展开图是一个半圆，则该圆锥的底面直径为________.5.圆台上、下底面面积分别是π、4π，侧面积是6π，这个圆台的体积是______月日高二数学天天练（114）姓名得分1.正方体各面所在平面将空间分成________部分.2.平行六面体ABCD—A1B1C1D1中，既与AB共面也与CC1共面的棱的条数为___.3.已知不重合的直线a，b和平面α，下面命题中正确的是________(填序号).①若a∥α，b⊂α，则a∥b；②若a∥α，b∥α，则a∥b；③若a∥b，b⊂α，则a∥α；④若a∥b，a∥α，则b∥α或b⊂α.4.已知平面α∥平面β，直线a⊂α，有下列说法，其中真命题的序号是________.①a与β内的所有直线平行；②a与β内无数条直线平行；③a与β内的任意一条直线都不垂直.5.已知l、m是空间两条不同直线，α、β是空间两个不同平面，给出下列四个条件：①平面α、β都垂直于平面γ；②平面α内存在不共线的三点到平面β的距离相等；③l、m是平面α内两条直线，且l∥β，m∥β；④l、m是两条异面直线，且l∥α，m∥α，l∥β，m∥β.其中可判断平面α与平面β平行的条件是________.(写出所有正确条件的序号）月日高二数学天天练（114）姓名得分1.正方体各面所在平面将空间分成________部分.2.平行六面体ABCD—A1B1C1D1中，既与AB共面也与CC1共面的棱的条数为___.3.已知不重合的直线a，b和平面α，下面命题中正确的是________(填序号).①若a∥α，b⊂α，则a∥b；②若a∥α，b∥α，则a∥b；③若a∥b，b⊂α，则a∥α；④若a∥b，a∥α，则b∥α或b⊂α.4.已知平面α∥平面β，直线a⊂α，有下列说法，其中真命题的序号是________.①a与β内的所有直线平行；②a与β内无数条直线平行；③a与β内的任意一条直线都不垂直.5.已知l 、m 是空间两条不同直线，α、β是空间两个不同平面，给出下列四个条件： ①平面α、β都垂直于平面γ；②平面α内存在不共线的三点到平面β的距离相等； ③l 、m 是平面α内两条直线，且l ∥β，m ∥β；④l 、m 是两条异面直线，且l ∥α，m ∥α，l ∥β，m ∥β.其中可判断平面α与平面β平行的条件是________.(写出所有正确条件的序号）月 日高二数学天天练（115） 姓 名 得 分1.若直线a 与平面α不垂直，那么在平面α内与直线a 垂直的直线有________条.2.m 、n 是空间中两条不同直线，α、β是两个不同平面，下面有四个命题： ①m ⊥α，n ∥β，α∥β⇒m ⊥n ；②m ⊥n ，α∥β，m ⊥α⇒n ∥β； ③m ⊥n ，α∥β，m ∥α⇒n ⊥β；④m ⊥α，m ∥n ，α∥β⇒n ⊥β. 其中，所有真命题的编号是________.3.已知平面α⊥β，α∩β＝l ，P 是空间一点，且P 到平面α、β的距离分别是1、2， 则点P 到l 的距离为________.4.设m ，n 是两条不同的直线，α，β是两个不同的平面，则下列四个命题，真命题的是________ ①若α∥β，m ⊂α，则m ∥β；②若m ∥α，n ⊂α，则m ∥n ； ③若α⊥β，m ∥α，则m ⊥β；④若m ⊥α，m ∥β，则α⊥β.5．在四面体O —ABC 中，OA →＝a ，OB →＝b ，OC →＝c ，D 为BC 的中点，E 为AD 的中点， 则OE →＝______________.(用a ，b ，c 表示)月 日高二数学天天练（115） 姓 名 得 分1.若直线a 与平面α不垂直，那么在平面α内与直线a 垂直的直线有________条.2.m 、n 是空间中两条不同直线，α、β是两个不同平面，下面有四个命题： ①m ⊥α，n ∥β，α∥β⇒m ⊥n ；②m ⊥n ，α∥β，m ⊥α⇒n ∥β； ③m ⊥n ，α∥β，m ∥α⇒n ⊥β；④m ⊥α，m ∥n ，α∥β⇒n ⊥β. 其中，所有真命题的编号是________.3.已知平面α⊥β，α∩β＝l ，P 是空间一点，且P 到平面α、β的距离分别是1、2， 则点P 到l 的距离为________.4.设m ，n 是两条不同的直线，α，β是两个不同的平面，则下列四个命题，真命题的是________ ①若α∥β，m ⊂α，则m ∥β；②若m ∥α，n ⊂α，则m ∥n ； ③若α⊥β，m ∥α，则m ⊥β；④若m ⊥α，m ∥β，则α⊥β.5．在四面体O —ABC 中，OA →＝a ，OB →＝b ，OC →＝c ，D 为BC 的中点，E 为AD 的中点， 则OE →＝______________.(用a ，b ，c 表示)月 日高二数学天天练（116） 姓 名 得 分1.已知a ＝(－3,2,5)，b ＝(1,5，－1)，则a ＋b ＝____________.2.若向量a ＝(1,1，x )，b ＝(1,2,1)，c ＝(1,1,1)，满足条件(c －a )·(2b )＝－2，则x ＝________.3.两不重合直线l 1和l 2的方向向量分别为v 1＝(1,0，－1)，v 2＝(－2，0,2)，则l 1与l 2的 位置关系是__________．4.设l 1的方向向量为a ＝(1,2，－2)，l 2的方向向量为b ＝(－2，3，m )，若l 1⊥l 2，则m ＝__.5.已知AB →＝(2,2,1)，AC →＝(4,5,3)，则平面ABC 的单位法向量为____________．月 日高二数学天天练（116） 姓 名 得 分1.已知a ＝(－3,2,5)，b ＝(1,5，－1)，则a ＋b ＝____________.2.若向量a ＝(1,1，x )，b ＝(1,2,1)，c ＝(1,1,1)，满足条件(c －a )·(2b )＝－2，则x ＝________.3.两不重合直线l 1和l 2的方向向量分别为v 1＝(1,0，－1)，v 2＝(－2，0,2)，则l 1与l 2的 位置关系是__________．4.设l 1的方向向量为a ＝(1,2，－2)，l 2的方向向量为b ＝(－2，3，m )，若l 1⊥l 2，则m ＝__.5.已知AB →＝(2,2,1)，AC →＝(4,5,3)，则平面ABC 的单位法向量为____________．月 日高二数学天天练（117） 姓 名 得 分1.若平面α、β的法向量分别为n 1＝(2，－3,5)，n 2＝(－3,1，－4)，则α、β的位置关系___.2.如果平面的一条斜线与它在这个平面上的射影的方向向量分别是a ＝(1,0,1)，b ＝(0,1,1)，那么，这条斜线与平面所成的角是________.3.若平面α的一个法向量为n ＝(4,1,1)，直线l 的一个方向向量为a ＝(－2，－3,3)，则l 与α所成角的正弦值为________.4.在长方体ABCD —A 1B 1C 1D 1中，AA 1＝5，AB ＝12，那么直线B 1C 1和平面A 1BCD 1的距离是________.5.正四棱锥S —ABCD 中，O 为顶点在底面上的射影，P 为侧棱SD 的中点，且SO ＝OD ，则直线BC 与平面P AC 的夹角的大小为________.月 日高二数学天天练（117） 姓 名 得 分1.若平面α、β的法向量分别为n 1＝(2，－3,5)，n 2＝(－3,1，－4)，则α、β的位置关系___.2.如果平面的一条斜线与它在这个平面上的射影的方向向量分别是a ＝(1,0,1)，b ＝(0,1,1)，那么，这条斜线与平面所成的角是________.3.若平面α的一个法向量为n＝(4,1,1)，直线l的一个方向向量为a＝(－2，－3,3)，则l与α所成角的正弦值为________.4.在长方体ABCD—A1B1C1D1中，AA1＝5，AB＝12，那么直线B1C1和平面A1BCD1的距离是________.5.正四棱锥S—ABCD中，O为顶点在底面上的射影，P为侧棱SD的中点，且SO＝OD，则直线BC与平面P AC的夹角的大小为________.月日高二数学天天练（118）姓名得分1.若直线斜率的绝对值等于1，则直线的倾斜角为____________.2.过点M(－2，m)，N(m,4)的直线的斜率等于1，则m的值为________.3.若点A(4,3)，B(5，a)，C(6,5)三点共线，则a的值为______.4.过点M(3，－4)，且在两坐标轴上的截距相等的直线的方程为__________________.5.已知直线l：ax＋y－2－a＝0在x轴和y轴上的截距相等，则a的值是____.月日高二数学天天练（118）姓名得分1.若直线斜率的绝对值等于1，则直线的倾斜角为____________.2.过点M(－2，m)，N(m,4)的直线的斜率等于1，则m的值为________.3.若点A(4,3)，B(5，a)，C(6,5)三点共线，则a的值为______.4.过点M(3，－4)，且在两坐标轴上的截距相等的直线的方程为__________________.5.已知直线l：ax＋y－2－a＝0在x轴和y轴上的截距相等，则a的值是____.月日高二数学天天练（119）姓名得分1.圆心在C(8，－3)，且经过点M(5,1)的圆的方程为______________.2.若方程x2＋y2＋ax＋2ay＋2a2＋a－1＝0表示圆，则a的取值范围是______________.3.已知圆C经过A(5,1)，B(1,3)两点，圆心在x轴上，则C的方程为______________.4.圆x2－2x＋y2－3＝0的圆心到直线x＋3y－3＝0的距离为________.5.过点A(1，－1)，B(－1,1)，且圆心在直线x＋y－2＝0上的圆的方程是__________________.月日高二数学天天练（119）姓名得分1.圆心在C(8，－3)，且经过点M(5,1)的圆的方程为______________.2.若方程x2＋y2＋ax＋2ay＋2a2＋a－1＝0表示圆，则a的取值范围是______________.3.已知圆C经过A(5,1)，B(1,3)两点，圆心在x轴上，则C的方程为______________.4.圆x2－2x＋y2－3＝0的圆心到直线x＋3y－3＝0的距离为________.5.过点A(1，－1)，B(－1,1)，且圆心在直线x＋y－2＝0上的圆的方程是__________________.月日高二数学天天练（120）姓名得分1.已知圆C经过M(2，－1)和直线x＋y＝1相切，且圆心在直线y＝－2x上，则圆C的方程为__________________________2.直线y＝ax＋1与圆x2＋y2－2x－3＝0的位置关系是________.3.若直线3x＋4y＋m＝0与圆x2＋y2－2x＋4y＋4＝0没有公共点，则实数m的取值范围是________.4.设直线ax－y＋3＝0与圆(x－1)2＋(y－2)2＝4相交于A、B两点，且弦AB的长为23，则a＝________.5.圆C1：x2＋y2＋2x＋2y－2＝0与圆C2：x2＋y2－4x－2y＋1＝0的公切线有且仅有___条.月日高二数学天天练（120）姓名得分1.已知圆C经过M(2，－1)和直线x＋y＝1相切，且圆心在直线y＝－2x上，则圆C的方程为__________________________2.直线y＝ax＋1与圆x2＋y2－2x－3＝0的位置关系是________.3.若直线3x＋4y＋m＝0与圆x2＋y2－2x＋4y＋4＝0没有公共点，则实数m的取值范围是________.4.设直线ax－y＋3＝0与圆(x－1)2＋(y－2)2＝4相交于A、B两点，且弦AB的长为23，则a＝________.5.圆C1：x2＋y2＋2x＋2y－2＝0与圆C2：x2＋y2－4x－2y＋1＝0的公切线有且仅有___条.月日高二数学天天练（121）姓名得分1.已知实数x，y满足x2＋y2＝1，则x－y的取值范围是____________.2.若圆(x－3)2＋(y＋5)2＝r2上有且只有两个点到直线4x－3y－2＝0的距离等于1，则半径r的取值范围为________.3.若圆(x－a)2＋(y－b)2＝b2＋1始终平分圆(x＋1)2＋(y＋1)2＝4的周长，则a，b满足关系式______________.4.已知曲线C：(x－1)2＋y2＝1，点A(－2,0)及点B(3，a)，从点A观察点B，要使视线不被曲线C挡住，则a的取值范围是______________.5.如果椭圆x2100＋y236＝1上一点P到焦点F1的距离等于6，那么点P到另一个焦点F2的距离是________.月日高二数学天天练（121）姓名得分1.已知实数x，y满足x2＋y2＝1，则x－y的取值范围是____________.2.若圆(x－3)2＋(y＋5)2＝r2上有且只有两个点到直线4x－3y－2＝0的距离等于1，则半径r的取值范围为________.3.若圆(x－a)2＋(y－b)2＝b2＋1始终平分圆(x＋1)2＋(y＋1)2＝4的周长，则a，b满足关系式______________.4.已知曲线C：(x－1)2＋y2＝1，点A(－2,0)及点B(3，a)，从点A观察点B，要使视线不被曲线C挡住，则a的取值范围是______________.5.如果椭圆x2100＋y236＝1上一点P到焦点F1的距离等于6，那么点P到另一个焦点F2的距离是________.月日高二数学天天练（122）姓名得分1.已知点F1(－4,0)和F2(4,0)，一曲线上的动点P到F1，F2距离之差为6，该曲线方程是____ _2.若中心在坐标原点，对称轴为坐标轴的椭圆经过两点(4,0)和(0,2)，则该椭圆的离心率等于________.3.已知F1、F2是椭圆C的左、右焦点，点P在椭圆上，且满足PF1＝2PF2，∠PF1F2＝30°，则椭圆的离心率为__________.4.已知F1，F2是椭圆x216＋y29＝1的两焦点，过点F2的直线交椭圆于A，B两点.在△AF1B中，若有两边之和是10，则第三边的长度为________.5.“－3<m<5”是“方程x25－m＋y2m＋3＝1表示椭圆”的____________条件.月日高二数学天天练（122）姓名得分2.已知点F1(－4,0)和F2(4,0)，一曲线上的动点P到F1，F2距离之差为6，该曲线方程是____ _2.若中心在坐标原点，对称轴为坐标轴的椭圆经过两点(4,0)和(0,2)，则该椭圆的离心率等于________.3.已知F1、F2是椭圆C的左、右焦点，点P在椭圆上，且满足PF1＝2PF2，∠PF1F2＝30°，则椭圆的离心率为__________.4.已知F1，F2是椭圆x216＋y29＝1的两焦点，过点F2的直线交椭圆于A，B两点.在△AF1B中，若有两边之和是10，则第三边的长度为________.5.“－3<m<5”是“方程x25－m＋y2m＋3＝1表示椭圆”的____________条件.月日高二数学天天练（123）姓名得分1.抛物线y2＝8x上到焦点的距离等于6的点的坐标是______________.2.双曲线mx2＋y2＝1的虚轴长是实轴长的2倍，则m＝_____________________.3.已知以双曲线C的两个焦点及虚轴的两个端点为顶点的四边形中，有一个内角为60°，则双曲线C的离心率为________.4.已知双曲线x2a2－y2b2＝1 (a>0，b>0)和椭圆x216＋y29＝1有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为______________.5.若双曲线x2a2－y2b2＝1 (a>0，b>0)的焦点到其渐近线的距离等于实轴长，则该双曲线的离心率为________.月日高二数学天天练（123）姓名得分1.抛物线y2＝8x上到焦点的距离等于6的点的坐标是______________.2.双曲线mx2＋y2＝1的虚轴长是实轴长的2倍，则m＝_____________________.3.已知以双曲线C 的两个焦点及虚轴的两个端点为顶点的四边形中，有一个内角为60°， 则双曲线C 的离心率为________.4.已知双曲线x 2a 2－y 2b 2＝1 (a >0，b >0)和椭圆x 216＋y 29＝1有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为______________.5.若双曲线x 2a 2－y 2b2＝1 (a >0，b >0)的焦点到其渐近线的距离等于实轴长，则该双曲线的离心率为________.月 日高二数学天天练（124） 姓 名 得 分1.已知椭圆的中心在原点，离心率e ＝12，且它的一个焦点与抛物线y 2＝－4x 的焦点重合，则此椭圆方程为__________.2.若双曲线x 2＋ky 2＝1的离心率是2，则实数k 的值是________________.3.椭圆9x 2＋25y 2＝225上一点M 到左焦点F 1的距离为2，N 是MF 1的中点，O 是坐标原 点，则ON ＝________.4.已知椭圆x 2a 2＋y 2b 2＝1 (a >b >0)的左焦点为F ，右顶点为A ，点B 在椭圆上，且BF ⊥x 轴，直线AB 交y 轴于点P .若AP →＝2PB →，则椭圆的离心率是________.5.设双曲线x 2a 2－y 2b 2＝1 (a >0，b >0)的渐近线与抛物线y ＝x 2＋1相切，则该双曲线的离心率为________.月 日高二数学天天练（124） 姓 名 得 分1.已知椭圆的中心在原点，离心率e ＝12，且它的一个焦点与抛物线y 2＝－4x 的焦点重合，则此椭圆方程为__________.2.若双曲线x 2＋ky 2＝1的离心率是2，则实数k 的值是________________.3.椭圆9x 2＋25y 2＝225上一点M 到左焦点F 1的距离为2，N 是MF 1的中点，O 是坐标原 点，则ON ＝________.4.已知椭圆x 2a 2＋y 2b 2＝1 (a >b >0)的左焦点为F ，右顶点为A ，点B 在椭圆上，且BF ⊥x 轴，直线AB 交y 轴于点P .若AP →＝2PB →，则椭圆的离心率是________.5.设双曲线x 2a 2－y 2b 2＝1 (a >0，b >0)的渐近线与抛物线y ＝x 2＋1相切，则该双曲线的离心率为________.月 日高二数学天天练（125） 姓 名 得 分1.与两条坐标轴的距离的积是常数k (k >0)的点的轨迹方程是______________.2.若抛物线y 2＝2px 的焦点与椭圆x 26＋y 22＝1的右焦点重合，则p 的值为________.3.动圆过点(1,0)，且与直线x ＝－1相切，则动圆的圆心的轨迹方程为__________.4.设抛物线y 2＝8x 上一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是________.5.已知点A (－2,0)、B (3,0)，动点P (x ，y )满足PA →·PB →＝x 2－6，则点P 的轨迹方程_______.月 日高二数学天天练（125） 姓 名 得 分1.与两条坐标轴的距离的积是常数k (k >0)的点的轨迹方程是______________.2.若抛物线y 2＝2px 的焦点与椭圆x 26＋y 22＝1的右焦点重合，则p 的值为________.3.动圆过点(1,0)，且与直线x ＝－1相切，则动圆的圆心的轨迹方程为__________.4.设抛物线y 2＝8x 上一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是________.5.已知点A (－2,0)、B (3,0)，动点P (x ，y )满足PA →·PB →＝x 2－6，则点P 的轨迹方程_______.月 日高二数学天天练（126） 姓 名 得 分1.已知l 1的倾斜角为45°，l 2经过点P (－2，－1)，Q (3，m )，若l 1⊥l 2，则实数m ＝________.2.若三条直线y ＝2x ，x ＋y ＝3，mx ＋2y ＋5＝0相交于同一点，则m 的值为________.3.已知直线l 1与l 2：x ＋y －1＝0平行，且l 1与l 2的距离是2，则直线l 1的方程为_____.4.(2010·安徽)过点(1,0)且与直线x －2y －2＝0平行的直线方程是______________.5.若经过点(3，a )、(－2,0)的直线与经过点(3，－4)且斜率为12的直线垂直，则a 的值为___.月 日高二数学天天练（126） 姓 名 得 分1.已知l 1的倾斜角为45°，l 2经过点P (－2，－1)，Q (3，m )，若l 1⊥l 2，则实数m ＝________.2.若三条直线y ＝2x ，x ＋y ＝3，mx ＋2y ＋5＝0相交于同一点，则m 的值为________.3.已知直线l 1与l 2：x ＋y －1＝0平行，且l 1与l 2的距离是2，则直线l 1的方程为_____.4.(2010·安徽)过点(1,0)且与直线x －2y －2＝0平行的直线方程是______________.5.若经过点(3，a )、(－2,0)的直线与经过点(3，－4)且斜率为12的直线垂直，则a 的值为___.月 日高二数学天天练（127） 姓 名 得 分1.从3名女同学和2名男同学中选1人主持本班的某次主题班会，则不同的选法种数为___.2.5位同学报名参加两个课外活动小组，每位同学限报其中的一个小组，则不同的报名方 法共有________种.3.有不同颜色的四件上衣与不同颜色的三件长裤，如果一条长裤与一件上衣配成一套，则不同的配法种数是________.4.8名世界网球顶级选手在上海大师赛上分成两组，每组各4人，分别进行单循环赛， 每组决出前两名，再由每组的第一名与另一组的第二名进行淘汰赛，获胜者角逐冠、亚军，败者角逐第3、4名，则大师赛共有________场比赛.5.有A 、B 两种类型的车床各一台，现有甲、乙、丙三名工人，其中甲、乙都会操作两种车床，丙只会操作A 种车床，现在要从三名工人中选2名分别去操作以上车床，则不同的选派方法有________种.月 日高二数学天天练（127） 姓 名 得 分1.从3名女同学和2名男同学中选1人主持本班的某次主题班会，则不同的选法种数为___.2.5位同学报名参加两个课外活动小组，每位同学限报其中的一个小组，则不同的报名方 法共有________种.3.有不同颜色的四件上衣与不同颜色的三件长裤，如果一条长裤与一件上衣配成一套，则不同的配法种数是________.4.8名世界网球顶级选手在上海大师赛上分成两组，每组各4人，分别进行单循环赛，每组决出前两名，再由每组的第一名与另一组的第二名进行淘汰赛，获胜者角逐冠、亚军，败者角逐第3、4名，则大师赛共有________场比赛.5.有A、B两种类型的车床各一台，现有甲、乙、丙三名工人，其中甲、乙都会操作两种车床，丙只会操作A种车床，现在要从三名工人中选2名分别去操作以上车床，则不同的选派方法有________种.月日高二数学天天练（128）姓名得分1.有4种不同的蔬菜，从中选出3种，分别种植在不同土质的3块土地上进行试验，有_____种不同的种植方法.2.从5人中选派3人去参加某个会议，不同的方法共有________种.3.某班级要从4名男生、2名女生中选派4人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案有________种.4. 5个人站成一排，其中甲、乙两人不相邻的排法有________种.5.某电视台连续播放5个广告，其中有3个不同的商业广告和2个不同的奥运宣传广告，要求最后播放的必须是奥运宣传广告，且2个奥运宣传广告不能连续播放，则不同的播放方式有________种.月日高二数学天天练（128）姓名得分2.有4种不同的蔬菜，从中选出3种，分别种植在不同土质的3块土地上进行试验，有_____种不同的种植方法.2.从5人中选派3人去参加某个会议，不同的方法共有________种.3.某班级要从4名男生、2名女生中选派4人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案有________种.4. 5个人站成一排，其中甲、乙两人不相邻的排法有________种.5.某电视台连续播放5个广告，其中有3个不同的商业广告和2个不同的奥运宣传广告，要求最后播放的必须是奥运宣传广告，且2个奥运宣传广告不能连续播放，则不同的播放方式有________种.月 日高二数学天天练（129） 姓 名 得 分1. (x －2y )7的展开式中第3项的二项式系数是________.2. x ⎝⎛⎭⎫x －2x 7的展开式中，x 4的系数是______.(用数字作答) 3.若(x －1)4＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4，则a 0＋a 2＋a 4的值为________.4.(若(x －ax 2)6展开式的常数项为60，则常数a 的值为________.5.若⎝ ⎛⎭⎪⎫3x －1x n 展开式中各项系数之和为32，则该展开式中含x 3的项的系数为_______.月 日高二数学天天练（129） 姓 名 得 分1. (x －2y )7的展开式中第3项的二项式系数是________.2. x ⎝⎛⎭⎫x －2x 7的展开式中，x 4的系数是______.(用数字作答) 3.若(x －1)4＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4，则a 0＋a 2＋a 4的值为________.4.(若(x －ax 2)6展开式的常数项为60，则常数a 的值为________.5.若⎝ ⎛⎭⎪⎫3x －1x n 展开式中各项系数之和为32，则该展开式中含x 3的项的系数为_______.月 日高二数学天天练（130） 姓 名 得 分1.用反证法证明命题：“a ，b ∈N ，ab 可被5整除，那么a ，b 中至少有一个能被5整除”时，假设的内容应为__________________.2.已知a 1＝3，a 2＝6，且a n ＋2＝a n ＋1－a n ，则a 33＝________.3.在平面上，若两个正三角形的边长比为1∶2，则它们的面积比为1∶4.类似地，在空间中，若两个正四面体的棱长比为1∶2，则它们的体积比为__________.4.要证明“3＋7<25”可选择的方法有以下几种，其中最合理的是________.(填序号) ①反证法，②分析法，③综合法.5.观察下列等式1＝1，2＋3＋4＝9，3＋4＋5＋6＋7＝25，4＋5＋6＋7＋8＋9＋10＝49 照此规律，第五个等式应为_______________________.月 日高二数学天天练（130） 姓 名 得 分1.用反证法证明命题：“a ，b ∈N ，ab 可被5整除，那么a ，b 中至少有一个能被5整除”时，假设的内容应为__________________.2.已知a 1＝3，a 2＝6，且a n ＋2＝a n ＋1－a n ，则a 33＝________.3.在平面上，若两个正三角形的边长比为1∶2，则它们的面积比为1∶4.类似地，在空间中，若两个正四面体的棱长比为1∶2，则它们的体积比为__________.4.要证明“3＋7<25”可选择的方法有以下几种，其中最合理的是________.(填序号) ①反证法，②分析法，③综合法.5.观察下列等式1＝1，2＋3＋4＝9，3＋4＋5＋6＋7＝25，4＋5＋6＋7＋8＋9＋10＝49 照此规律，第五个等式应为_______________________.月 日高二数学天天练（131） 姓 名 得 分1.在应用数学归纳法证明凸n 边形的对角线为12n (n －3)条时，第一步检验第一个值n 0＝___.2.用数学归纳法证明：“1＋a ＋a 2＋…＋a n ＋1＝1－a n ＋21－a (a ≠1)”，在验证n ＝1时，左端计算所得的项为________.3.用数学归纳法证明：“1＋12＋13＋…＋12n －1<n (n >1)”，由n ＝k (k >1)不等式成立，推证n ＝k ＋1时，左边应增加的项的项数是________.4.记凸k 边形的内角和为f (k )，则凸k ＋1边形的内角和f (k ＋1)＝f (k )＋________.5.设a 、b ∈R ，若a －|b |>0，则下列不等式中正确的是________.(填序号) ①b －a >0; ②a 3＋b 3<0； ③a 2－b 2<0; ④b ＋a >0.月 日高二数学天天练（131） 姓 名 得 分。

高二数学天天练（02） 姓名一、选择题：1.若6＜x≤10 ，3≤y＜20，则x+y的范围是（）A.（9 30）B.[ 9 30）C.（9 30]D.[9 30]2.若a>b>c,则下列不等式成立的是（）A . B. ac>bcC .D .ac<bc3、若角满足的范围是（）A、（）B、C、（）D、（0）4、已知a>b,c>d则下列不等式成立的是( )A.4a+8c>4b+8dB.4a+8d>4b+8cC.4a-8c>4b-8dD.4a+4c>8b+8d5、已知,那么a,b,c三者之间的大小关系为（）A、a<b<cB、a<c<bC、c<a<bD、c<b<a6、已知>1，则下列各式中不成立的是（）A. a>bB.C. 0< D .b>0时a>b;b<0时a<b7、若a,b是任意实数,且a>b则( )A. a2>b2B.C. lg(a-b)>0D.(1/2)a<(1/2)b8、下列命题正确的是（）A、ac<bc =>a<bB、ac2<bc2 =>a<bC、a<b =>a2<b2D、a>b,c>d =>ac>bd二、填空题9、若a>b,c>d且a<0,d<0则ac bd10、若a>0>b>c>-1则a-bc b-ac11、已知a>0,b<0,a+b>0则a,b,-a,-b的大小关系12、若a>b,1<c<10则algc blgc三、解答题13、已知求a+b,a-b和ab的取值范围14、当c>a>b>0时，比较的大小15、已知a,b均为正实数b,cR且a>b,b>c+d.求证:ab>ac+bd。

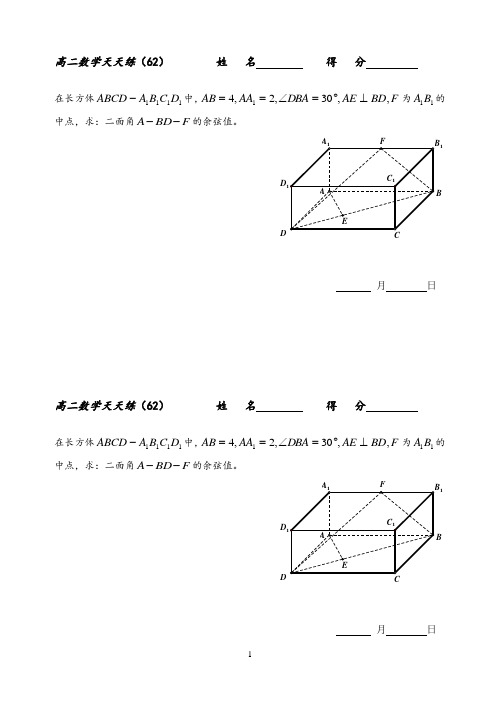
在长方体1111D C B A ABCD -中，F BD AE DBA AA AB ,,30,2,41⊥︒=∠==为11B A 的中点，求：二面角F BD A --的余弦值。

B1DD月 日高二数学天天练（62） 姓 名 得 分在长方体1111D C B A ABCD -中，F BD AE DBA AA AB ,,30,2,41⊥︒=∠==为11B A 的中点，求：二面角F BD A --的余弦值。

B1DD月 日1、已知抛物线y＝ax2＋bx－5在点(2,1)处的切线为y＝－3x＋7，则a＝______，b＝______.2、已知直线y＝kx＋1与曲线y＝x3＋ax＋b切于点(1,3)，则b的值为______3、函数y＝12x2－ln x的单调减区间为4、已知f(x)＝(x2＋x)(x－1)，则f′(2)等于________5、若函数f(x)＝x3＋bx2＋cx＋d的单调减区间为[－1,2]，则b＝__ _，c＝___月日高二数学天天练（63）姓名得分1、已知抛物线y＝ax2＋bx－5在点(2,1)处的切线为y＝－3x＋7，则a＝______，b＝______.2、已知直线y＝kx＋1与曲线y＝x3＋ax＋b切于点(1,3)，则b的值为______3、函数y＝12x2－ln x的单调减区间为4、已知f(x)＝(x2＋x)(x－1)，则f′(2)等于________5、若函数f(x)＝x3＋bx2＋cx＋d的单调减区间为[－1,2]，则b＝__ _，c＝___月日1、若函数y ＝－x 3＋6x 2＋m 的极大值等于13，则实数m 等于________2、若函数f (x )＝x 2＋ax ＋1在x ＝1处取极值，则a ＝______3、函数f (x )＝x 3－3x ＋1在闭区间[－3,0]上的最大值是________，最小值是_______4、函数f (x )＝x (1－x 2)在[0,1]上的最大值为______5、已知某矩形广场面积为4万平方米，则其周长至少为________米月 日高二数学天天练（64） 姓 名 得 分1、若函数y ＝－x 3＋6x 2＋m 的极大值等于13，则实数m 等于________2、若函数f (x )＝x 2＋ax ＋1在x ＝1处取极值，则a ＝______3、函数f (x )＝x 3－3x ＋1在闭区间[－3,0]上的最大值是________，最小值是_______4、函数f (x )＝x (1－x 2)在[0,1]上的最大值为______5、已知某矩形广场面积为4万平方米，则其周长至少为________米月 日高二数学天天练（65） 姓 名 得 分 设1=x 与2=x 是函数x bx x a x f ++=2ln )(的两个极值点． （1）试确定常数a 和b 的值；（2）试判断2,1==x x 是函数)(x f 的极大值还是极小值，并说明理由．月 日高二数学天天练（65） 姓 名 得 分 设1=x 与2=x 是函数x bx x a x f ++=2ln )(的两个极值点． （1）试确定常数a 和b 的值；（2）试判断2,1==x x 是函数)(x f 的极大值还是极小值，并说明理由．月 日高二数学天天练（66） 姓 名 得 分 已知函数a x x x x f +++-=93)(23。

高二数学天天练（45） 姓名课题:椭圆的简单几何性质（1） 一、选择题：1.椭圆6x 2+y 2=6的长轴的端点坐标是 [ ]A.（-1，0），（1，0）B.（-6，0），（6，0）C.（-6，0），（6，0）D.（0，-6），（0，6） 2.已知点（3，2）在椭圆b 2x 2+a 2y 2=a 2b 2上，则 [ ] A.点（-3，-2）不在椭圆上 B.点（3，-2）不在椭圆上 C.点（-3，2）在椭圆上D.无法判断点（-3，-2），（3，-2），（-3，2）是否在椭圆上 3.椭圆3x 2+2y 2=1的焦点坐标是[ ] A.（0，-66），（0，66） B.（0，-1），（0，1） C.（-1，0），（1，0） D.（-66，0），（66，0）4.椭圆的短轴的一个端点到一个焦点的距离是5，焦点到椭圆中心的距离为3，则椭圆的标准方程是[ ]A.191622=+y x 或116922=+y x B. 192522=+y x C.1162522=+y x 或1251622=+y x D.椭圆的方程无法确定 5.椭圆的一焦点与两顶点为等边三角形的三个顶点，则长轴是短轴长的 [ ] A.3倍 B.2倍 C.2倍 D.32倍 6.椭圆的一个焦点与短轴两顶点组成一个等边三角形，则椭圆的离心率为 [ ] A.23 B.43 C. 22D. 217.椭圆12222=+by a x 和λ=+2222b y a x （λ>0)具有 [ ]A.相同的焦点B.相同的顶点C.相同的离心率D.相同的长、短轴8.已知椭圆1522=+m y x 的离心率 =510，则m 的值为 [ ] A.3 B.3或35 C.15 D. 15或3155 二填空题：9.对于椭圆x 2+ky 2=2（0<k<1)，k 越接近 椭圆越扁，k 越接近 椭圆越接近圆.10.由椭圆短轴的一个端点看长轴的端点的视角为1200，则离心率为 . 11.若椭圆b 2x 2+a 2y 2=a 2b 2（a>b>0)的左焦点为F 1，右顶点A ，左顶点为B ，且离心率为215-，则∠ABF 1= . 12.中心在原点，焦点在x 轴，若长轴为18，且两个焦点恰好将长轴三等分，则此椭圆的方程是 .三、解答题： 13.求符合下列条件的椭圆标准方程： ①焦距为8，离心率为0.8②焦点与长轴较接近的端点的距离为510-，焦点与短轴两端点的连线互 相垂直.14.已知椭圆的对称轴是坐标轴，O 为坐标原点，F 是一个焦点，A 是一个顶点，若椭圆的长轴是6，且cos ∠OFA=32,求椭圆方程.。

高二数学天天练（77） 姓名课题：不等式性质一、选择题：1.不等式a>b 和b a 11>同时成立的充要条件是 [ ] A.a>b>0 B.a>0>b C.011<<a b D. b a 11>>02.若x<1，则下列关系式正确的是 [ ] A.x 1>1 B.x 3<1 C.x 2<1 D.|x|<13.a>b>c 且a+b+c=0则 [ ]A.ab>bcB.ac>bcC.ab>acD.a|b|>c|b|4.与a>b 等价的不等式是 [ ]A.|a|>|b|B.a 2>b 2C.a b>1 D.b a 22>5.a<c 是a 2<c 2成立的 [ ]A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.a>b>0,x>0则x a xb ++的范围是 [ ] A. x a x b ++<1 B. x a x b ++>1 C.a b < x a x b ++<1 D. x a xb ++<a b7.设a ，b ，c ∈R ，下面各不等式正确的是 [ ]A.a 2+b 2≥2|ab|B.a+b ≥2abC.a 3+b 3+c 3≥3abcD.33abc cb a ≥++8.若x 、y ∈R ，且x+y=5，则3x +3y 的最小值是 [ ] A.10 B.63 C.46 D.1839.已知a ＞1，那么a+11-a 的最小值是 [ ] A.12-a a B.5+1 C.3 D.210.若x ＞y ＞1，a=21（lgx+lgy ），b=y x lg lg ，c=lg 2yx +，则 [ ]A.c ＜b ＜aB.b ＜a ＜cC.b ＜c ＜aD.a ＜b ＜c二、填空题： 11.已知x ＞y ＞0，且xy=1，则y x y x -+22的最小值是 . 12.实数x 、y 满足x 2+y 2=3，那么2+x y 的最大值是 . 三、解答题： 13.某小区要建一座中心对称的八边形的休闲小区，它的立体造型的平面图是由 两个相同的矩形ABCD 和EFGH 构成的面积为200平方米的十字型地域，计划在 正方形MNPQ 上建一座花坛，造价为每平方米4200元，在四个相同的矩形上 （图中阴影部分）铺花岗岩地平，造价为每平方米210元，再在四个角上铺草 坪造价为每平方米80元： （1） 设总造价为S 元，AD 长为x 米，试建立S 关于x 的关系式； （2） 当x 为何值时，S 最小，并求出这个最小值. B。

高二数学天天练（62） 姓名课题：§9.2空间直线(1) 一、选择题：1.空间四边形ABCD 的线段AB ，BC ，CD ，DA ，AC ，BD 中，互相成异面直线共有[ ] A.3对 B.2对 C.1对 D.0对2.正方体ABCD —A 1B 1C 1D 1中，与BA 1异面的棱共有[ ]A.12条B.8条C.6条D.4条3.在空间，如果一个角的两边与另一个角的两边分别平行，则这两个角 [ ]A.相等B.互补C.相等或互补D.既不相等也不互补4.不重合的两条直线a ，b 与直线l 都成异面直线，则a 与b 的位置关系是 [ ] A.平行或相交或异面 B.相交或平行 C.平行 D.异面5.异面直线a ，b 分别在平面α和β内，若α β=L ，则直线L 必定[ ] A.分别与a ，b 相交 B.与a ，b 都不相交 C.至多与a ，b 中的一条相交 D.至少与a ，b 中的一条相交 6.两条异面直线指的是[ ]A.在空间内不相交的两条直线B.分别位于两个不同平面内的两条直线C.某一个平面内的一条直线和这个平面外的一条直线D.不同在任何一个平面内的两条直线 二、填空题：7.不平行的两条直线的位置关系是 8.无公共点的两条直线的位置关系是9.直线a 和b 是异面直线，直线c//a 那么b 与c 的位置关系是 . 10.已知E 、F 分别平行四边形ABCD 的AD 、BC 中点，将平行四边形沿EF 折叠时， AB 、CD 关系是 . 三、解答题：11.已知E 、F 、G 、H 分别为空间四边形的边AB 、BC 、CD 、DA 的中点，对角线AC=6，BD=8，求EF 2+EH 2的值.12.已知E 和F 分别是正方体ABCD-A 1B 1C 1D 1的棱AA 1和棱CC 1上的点，且AE=C 1F ， 求证：四边形EBFD 是平行四边形.D 1BCDA1B1C 1E F GA BCD E FH。

数学练习题及答案高二第一节：选择题1. 若函数 f(x) = ax^2 + bx + c 的图象开口向上，且在点 P(-1, 3) 有极值，那么 a, b, c 的关系是（）(A) a ≠ 0, b = 0, c ≠ 0;(B) a ≠ 0, b ≠ 0, c ≠ 0;(C) a ≠ 0, b ≠ 0, c = 0;(D) a ≠ 0, b = 0, c = 0;答案：(A)解析：由题可知，函数图象开口向上，所以a ≠ 0。

又因为在点 P(-1, 3) 有极值，极值对应的 x 坐标为 -1，代入函数可得 f(-1) = -a + b - c。

由于函数开口向上，所以该极值为极小值，即 f(-1) = -a + b - c > 0。

再结合a ≠ 0，可以得出 b = 0，因为如果b ≠ 0，则在 x = -1 附近 f(-1)不可能为正值。

所以，a ≠ 0，b = 0，c ≠ 0。

2. 已知函数 y = 2x^2 + 3x - 2 的图象与 x 轴交于点 A、B两个地方，那么点 A、B 的纵坐标分别是（）(A) 0，-3;(B) -2，0;(C) 0，-2;(D) -3，0;答案：(C)解析：当函数与 x 轴交于点 A、B 时，函数值 y = 2x^2 + 3x - 2 = 0。

可以通过因式分解或二次方程求根公式来解。

将方程 2x^2 + 3x - 2 = 0 因式分解为 (2x + 1)(x - 2) = 0，得到两个解：x = -1/2，x = 2。

所以，点 A 的纵坐标为 y(A) = 2(-1/2)^2 + 3(-1/2) - 2 = -2，点 B 的纵坐标为 y(B) = 2(2)^2 + 3(2) - 2 = -2。

因此，点 A、B 的纵坐标分别是 0、-2。

第二节：填空题1. 给定矩阵 A = [1 2 3; -1 0 1]，则 A 的转置矩阵为 ______。

答案：[1 -1; 2 0; 3 1]解析：矩阵的转置就是将原矩阵的行变为列，列变为行。

高二数学天天练（59） 姓名 课题：抛物线的几何性质（2）一、选择题：1.已知抛物线x 2=8y ，过焦点F ，倾斜角为43π的直线交抛物线于A 、B 两点，则线段AB 的长为A.8 B.82 C.16 D.162 [ ] 2.抛物线顶点在坐标原点，以x 轴为对称轴，过焦点且与y 轴垂直的弦长为16，则抛物线方程为 [ ]A.x 2=±8yB.x 2=16yC.x 2=±16yD.y 2=±16x3.抛物线y=ax 2（a>0)与直线y=kx+b （k ≠0）有两个公共点，其横坐标分别是x 1，x 2，而直线y=kx+b 与x 轴交点的横坐标是x 3，则x 1，x 2，x 3之间的关系是 [ ]A. x 3=x 1+x 2B. x 3=21x 1x 1+ C.x 1x 3=x 1x 2+x 2x 3 D.x 1x 2=x 1x 3+x 2x 3 4.直线2x-2y+3=0被曲线y=2x 2截得的线段中点到原点的距离为 [ ] A.429 B.229 C.29 D.29 5.若直线y=kx+1与抛物线y 2=x 仅有一个公共点，则k 的值为 [ ] A.41 B.0或41 C.0或-43 D. 41或-43 6.抛物线y 2=12x 截直线y=2x+1所得弦长等于[ ] A.15 B.215 C.215 D.15 7.过抛物线y 2=2px （p>0)的焦点作一条直线交抛物线于A （x 1，y 1）、B （x 2，y 2），则 2121x x y y 为 [ ] A.4 B.-4 C.p 2 D.-p 28.抛物线y 2=-8x 中以（-1，1）为中点的弦的方程是 [ ]A.x-4y-3=0B.x+4y+3=0C.4x+y-3=0D.4x+y+3=0二.填空题：9.直线y=x+b 与抛物线y 2=-3x 交于A 、B 两点，且线段中点的横坐标为-2， 则b= .10.已知抛物线y 2=x ，直线L 过点（0，-1）且与抛物线只有一个公共点，则直线 的方程是 . 11.过抛物线y 2=4x 焦点弦的中点轨迹方程是 . 12.正方形ABCD 顶点A 、B 在抛物线y=x 2上，C 、D 在直线y=x-4上，则正方形ABCD 面积是 . 三、解答题： 13.已知△ABC 的三个顶点都在抛物线y 2=32x 上，顶点A （2，8），三角形重心恰好是抛物线焦点，求BC 所在直线方程.。

高二数学天天练（49） 姓名课题：双曲线及其标准方程(1) 一、选择题：1.在双曲线的标准方程中，已知a=6,b=8.则其方程是[ ]A.1643622=-y x B.1366422=-y x C.1643622=-x y D.1643622=-y x 或1643622=-x y 2.已知F 1,F 2为定点，||PF 1|-|PF 2||=2a ，则动点A 的轨迹是 [ ] A.焦点为F 1，F 2的双曲线 B.不存在 C.以F 1，F 2为端点且方向相反且无公共点的两条直线 D.以上都不对3.方程6)4()4(2222=++-+-y x y x ，化简结果是[ ] A.17922=-y x B.17922=-y x (x ≥3) C.17922=-y x (x ≤-3) D.192522=-y x 4.已知方程11122=--+ky k x 表示双曲线，则k 的取值范围是 [ ] A.-1<k<1 B.k>0 C.k ≥0 D.k>1或k<-1 5.双曲线14122222=--+m y m x 的焦距是 [ ]A.4B.22C.8D.与m 无关6.在方程mx 2-my 2=n 中，若mn<0，则方程的曲线是 [ ]A.焦点在x 轴上的椭圆B.焦点在x 轴上的双曲线C.焦点在y 轴上的椭圆D.焦点在y 轴上的双曲线7.焦点分别是(0,-2),(0,2),且经过点P(-3,2)的双曲线的标准方程是[ ]A.1322=-y x B.1322=-x y C.1322=-x y D.12222=-y x 8.若P 是以F 1，F 2为焦点的双曲线192522=-y x 上的一点，且|PF 1|=12， 则|PF 2|= [ ]A.2或22B.3C.4D.5 二、填空题：9.双曲线2kx 2-ky 2=1的一个焦点是F(0,4)，则k 的值为10.双曲线1422=-y k x 的焦点坐标为 11.已知△ABC 的顶点A(0,-4),B(0,4),且4(sinB-sinA)=3sinC,则顶点C 的轨迹方程是12.若方程14922=---ky k x 表示双曲线，则实数k 的取值范围是 13.若椭圆14222=+m y x 与双曲线1222=-y m x 有相同的焦点，则实数m 的值为 14.设双曲线1162522=-y x 的焦点是F 1，F 2，直线L 过F 1且与双曲线的同一支交于A,B 两点，已知|AB|=8，则△ABF 2的周长为 三、解答题：13.求符合下列条件的双曲线的标准方程：①a=25,经过点A(-5,2)，且焦点在x 轴上； ②过两定点(3,415),(316,5)。

高二数学天天练（45） 姓名课题:椭圆的简单几何性质（1） 一、选择题：1.椭圆6x 2+y 2=6的长轴的端点坐标是 [ ]A.（-1，0），（1，0）B.（-6，0），（6，0）C.（-6，0），（6，0）D.（0，-6），（0，6） 2.已知点（3，2）在椭圆b 2x 2+a 2y 2=a 2b 2上，则 [ ] A.点（-3，-2）不在椭圆上 B.点（3，-2）不在椭圆上 C.点（-3，2）在椭圆上D.无法判断点（-3，-2），（3，-2），（-3，2）是否在椭圆上 3.椭圆3x 2+2y 2=1的焦点坐标是[ ] A.（0，-66），（0，66） B.（0，-1），（0，1） C.（-1，0），（1，0） D.（-66，0），（66，0）4.椭圆的短轴的一个端点到一个焦点的距离是5，焦点到椭圆中心的距离为3，则椭圆的标准方程是[ ]A.191622=+y x 或116922=+y xB. 192522=+y x C.1162522=+y x 或1251622=+y x D.椭圆的方程无法确定 5.椭圆的一焦点与两顶点为等边三角形的三个顶点，则长轴是短轴长的 [ ] A.3倍 B.2倍 C.2倍 D.32倍 6.椭圆的一个焦点与短轴两顶点组成一个等边三角形，则椭圆的离心率为 [ ] A.23 B.43 C. 22 D. 217.椭圆12222=+by a x 和λ=+2222b y a x （λ>0)具有 [ ]A.相同的焦点B.相同的顶点C.相同的离心率D.相同的长、短轴8.已知椭圆1522=+my x 的离心率 =510，则m 的值为 [ ]A.3B.3或35C.15D. 15或3155二填空题：9.对于椭圆x 2+ky 2=2（0<k<1)，k 越接近 椭圆越扁，k 越接近 椭圆越接近圆.10.由椭圆短轴的一个端点看长轴的端点的视角为1200，则离心率为 . 11.若椭圆b 2x 2+a 2y 2=a 2b 2（a>b>0)的左焦点为F 1，右顶点A ，左顶点为B ，且离心率为215-，则∠ABF 1= . 12.中心在原点，焦点在x 轴，若长轴为18，且两个焦点恰好将长轴三等分，则此椭圆的方程是 .三、解答题： 13.求符合下列条件的椭圆标准方程： ①焦距为8，离心率为0.8②焦点与长轴较接近的端点的距离为510-，焦点与短轴两端点的连线互 相垂直.14.已知椭圆的对称轴是坐标轴，O 为坐标原点，F 是一个焦点，A 是一个顶点，若椭圆的长轴是6，且cos ∠OFA=32,求椭圆方程.。