2017-2018年新观察元调模拟三附答案

2018届武汉市部分高中高三年级元调考试模拟训练化学试卷2018届武汉市部分高中高三年级元调考试模拟训练化学试卷本试卷共300分，考试用时150分钟。

本卷分第Ⅰ卷（选择题）和第Ⅱ卷（必考题和选考题）两部分。

第Ⅰ卷1 至5 页，第Ⅱ卷6至16页。

本卷共16页。

第Ⅰ卷（选择题共126分）本卷共21小题，每小题6分，共126分。

可能用到的相对原子质量：H 1Li 7 C 12O 16 Na 23 Fe 56Se 79一、选择题：本大题共13小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

7．化学与生活、社会发展息息相关。

下列说法不正确．．．的是A．用SO2漂白过的草帽日久会变色B．用天燃气代替煤作燃料可减少大气污染C．“84消毒液”杀死病菌是因为蛋白质变性D．乙醇用作医用消毒剂时，无水乙醇消毒效果最好8．设N A为阿伏加德罗常数的值。

下列有关叙述正确的是A．107 g Fe(OH)3胶体中胶体粒子的数目为N AB ．2 mol SO 2 与1 mol O 2反应生成的SO 3分子数为2N AC ．14 g 分子式为C n H 2n 的链烃中含有的碳碳双键的数目为n N AD ．7.8 g Na 2O 2与足量水反应转移的电子数为 0.2N A9．已知甲苯的结构简式为，其二氯代物的同分异构体有A ．7种B ．8种C ．9种D ．10种 10．下列选用的仪器和药品能达到实验目的的是AB C D尾气吸收Cl 2 吸收CO 2中的HCl 杂质 蒸馏时的接收装置 乙酸乙酯的收集装置 11．碱性硼化钒—空气电池工作时反应为：4VB 2＋11O 2===4B 2O 3＋2V 2O 5，室温下用该电池为电源，用惰性电极电解饱和氯化钠溶液，装置如图。

当外电路中通过0.04 mol 电子时，乙装置中溶液的体积为400 mL 。

则下列说法正确的是A ．外电路中电子由a 电极流向b 电极B ．c 电极上生成气体的体积为4.48 L —CH 3 NaOH 溶液 饱和NaHCO 3饱和碳酸钠溶液 VB 2电极 a KOH 溶液空气 甲 b cNaCl 溶液乙W、X原子的最外层电子数之比为5∶2，Z原子比X原子的核外电子数多5。

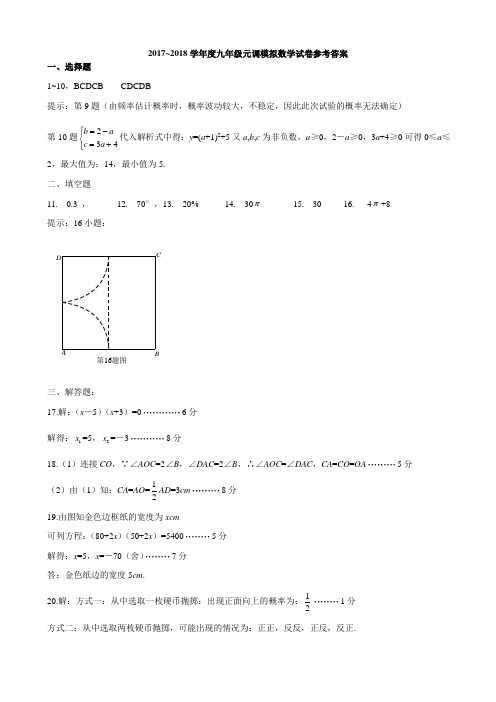
2017~2018学年度九年级元调模拟数学试卷参考答案一、选择题1~10，BCDCB CDCDB提示：第9题（由频率估计概率时，概率波动较大，不稳定，因此此次试验的概率无法确定）第10题234b ac a =-⎧⎨=+⎩代入解析式中得：y =(a +1)2+5又a ,b ,c 为非负数，a ≥0，2－a ≥0，3a +4≥0可得0≤a ≤2，最大值为：14，最小值为5. 二、填空题11. 0.3 ， 12. 70°，13. 20% 14. 30π 15. 30 16. 4π+8 提示：16小题：第16题图三、解答题：17.解：（x －5）（x +3）=0············6分 解得：1x =5，2x =－3···········8分18.（1）连接CO ，∵∠AOC =2∠B ，∠DAC =2∠B ，∴∠AOC =∠DAC ，CA =CO =OA ·········5分 （2）由（1）知：CA =AO =12AD =3cm ·········8分 19.由图知金色边框纸的宽度为xcm可列方程：（80+2x ）（50+2x ）=5400········5分 解得：x =5，x =－70（舍）········7分 答：金色纸边的宽度5cm .20.解：方式一：从中选取一枚硬币抛掷：出现正面向上的概率为：12········1分方式二：从中选取两枚硬币抛掷，可能出现的情况为：正正，反反，正反，反正.出现一正一反的概率为：12········3分方式三：从中选取三枚硬币抛掷，出现两个反面以上的概率为：12········6分故方式一：出现正面向上的概率与方式二：出现一正一反的概率 和方式三：出现两个反面以上的概率相等········8分正反反正正反正反反正正反反正21.（1）连OA ，∵OC =CB ，CA =12OB ，∴CA =CO －CB ，∠CAO =∠COA ，∠CAB =∠CBA ， 2（∠CAO +∠CAB ）=180°，∠OAB =90°，·······3分 （2）由（1）知：OA =OC =CA , ∠AOC =60°，∠CDA =12∠AOC =30°，过A 作AE ⊥CD ，则CE =AE ，DE. ∵∠ACD =45°，∴∠AOD =90°，ADAE －CEDE，CD =CE+DE······8分22.（1）y =－2x +200（30≤x ≤60）·······2分 （2）y =－2x 2+260x －6000（30≤x ≤60）·······4分 （3）y =－2（x －65）2+2450对称轴为x =65，a =－2＜0，开口向下，当30≤x ≤60时，y 随x 的增大而增大； 当x =60时，函数存在最大值为y =2400·······7分答：当单价为60元时，该公司日获利最大，最大利润为2400元 ······8分23.（1）ACBC =1，BF =3，连EB =5 ·····2分 （2）此题方法较多，酌情给分延长FM 至点P ，使得FM =MP ，连接AP ，DP ，先证△MEF ≌△MAP （SAS ） 得：AP =EF =CF 且AP //EF ，延长P A 交CF 于点K ，知P A ⊥CF ，则∠DAK +∠DCK =180°，则∠P AD =∠FCD ，△P AD ≌△FCD （SAS ） DP =DF ，∠DP A =∠DFC ，∴∠PDF =∠PKF =90°，则MD =MF ，MD ⊥MF ·····7分K P图2CDBAF EM（3）连接AC ，取中点为O OM =12CEO 为定点，OM 为定长，所以M 点的运动轨迹为O 为圆心当△ABC 旋转一周时，M 的轨迹为整个圆，因此路径长为：π ·····10分 24.解：（1）y =m （x 2+12x ）+x 2－2x －3，x 2+12x =0，即x =0或x =12时，y 的值与m 无关，当x =0时，y =－3；当x =－12时，y =－74，∴该定点为（－12，－74）·····3分 （2）m =0时，y =x 2－2x －3，∵P （2，a ），∴22－2×2－3=a ，∴P （2，－3），设1l 的解析式为y =kx +b ，∴2k +b =－3，∴b =－2k －3，∴1l ：y =kx －2k －3，联立22323y kx k y x x =--⎧⎨=--⎩得x 2－（2+k ）x +2k =0，∵△=0，∴[－2（2+k ）]2 －4×1×2k =0，∴k =2，1l ：y =2x －7 ·····7分（3）过点Q 作直线l //x 轴，过M 作ME ⊥l 于点E ，过N 作NF ⊥l 于点F ，∵MQ =NQ ，∴△MQE ≌△NQF ，∴QE =QF ，∴E x －Q x =Q x －F x ，即M x －P x =P x －N x ，∴M x +N x =2P x =2×2=4，联立223y kx b y x x =+⎧⎨=--⎩得x 2－（k +2）x －3－b =0，∴M x +N x =k +2，∴k +2=4，∴k =2·····12分。

2017—2018学年度高三第三次调研测试理科数学本试卷共23小题，共150分，共6页，考试时间120分钟，考试结束后，将答题卡和试题卷一并交回。

注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条 形码、姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。

2．选择题答案使用2B 铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案 的标号；非选择题答案必须使用0.5毫米黑色字迹的签字笔书写，字体工整、 笔迹清楚。

3．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案 无效。

4. 作图可先用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5. 保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮 纸刀。

一、选择题：本大题共12题，每小题5分，共60分，在每小题给出的四个选项中，只有一个是符合题目要求。

1. 若集合{|0}B x x =≥，且A B A =，则集合A 可以是A ．{1,2}B ．{|1}x x ≤C ．{1,0,1}-D ．R2． 已知复数1z i =+（i 为虚数单位）给出下列命题：①||z =；②1z i =-；③z 的虚部为i . 其中正确命题的个数是A. 0B. 1C. 2D. 33． 若1sin ,3α=且2παπ<<，则sin 2α=A ．B ．C ．D ． 4. 已知等差数列{}n a 的公差不为0，11a =，且248,,a a a 成等比数列，设{}n a 的前n 项和为n S ，则n S =A. (1)2n n +B. 2(1)2n +C. 212n + D. (3)4n n +5． 若1()n x x-的展开式中只有第7项的二项式系数最大，则展开式中含2x 项的系数是A ． 462-B ． 462C ． 792D ． 792-6． 执行如图所示的程序框图，输出的S 值为 A.12018B. 12019C. 20172018D. 201820197． 10|1|x dx -=⎰A ．12B ． 1C ． 2D ． 38． 一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是 (0,0,0),(1,0,1),(0,1,1)1,(,1,0)2,绘制该四面体三视图时,按照如图所示的方向画正视图,则得到左视图可以为 A.B.C.D.9． 设曲线()cos (*)f x m xm R =∈上任一点(,)x y 处切线斜率为()g x ，则函数2()y x g x =的部分图象可以为10．平行四边形ABCD 中，2,1,1,AB AD AB AD ===-点M 在边CD 上，则MA MB 的 最大值为A. 2B. 1C. 5D.111． 等比数列{}n a 的首项为32，公比为12-，前n 项和为n S ，则当*n N ∈时，1n nS S -的最 大值与最小值的比值为A. 125-B. 107- C. 109D.12512．已知函数13,1()22ln ,1x x f x x x ⎧+≤⎪=⎨⎪>⎩（ln x 是以e 为底的自然对数， 2.71828e =），若存在实数,()m n m n <，满足()()f m f n =，则n m -的取值范围为 A. 2(0,3)e +B. 2(4,1]e -C. 2[52ln2,1]e --D. [52ln2,4)-二、填空题：本大题共4个小题,每小题5分。

吉林市普通中学2017—2018学年度高中毕业班第三次调研测试二、选择题：本题共8题，每小题6分。

在每小题给出的四个选项中，第14—18题只有一项符合题目要求，第19—21题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分。

14. 下列说法正确的是A ．光电效应是原子核吸收光子向外释放电子的现象B ．天然放射性现象说明原子核具有复杂的结构C ．一个氘核的质量等于一个质子和一个中子的质量和D ．已知钴60的半衰期为5.27年,则任一个钴60原子核都将在5.27年内发生衰变15．如图所示，竖直平面内放一直角杆MON ，杆的水平部分粗糙，动摩擦因数μ＝0.2，杆的竖直部分光滑。

杆的两部分各套有质量均为1 kg的小球A 和B ，A 、B 球间用细绳相连。

初始A 、B 均处于静止状态，已知OA ＝3 m ，OB ＝4 m ，若A 球在水平拉力的作用下向右缓慢地移动1 m(取g ＝10 m/s 2)，那么该过程中拉力F 做功为A ．4 JB ．6 JC ．10 JD ．14 J16．如图甲所示，以斜面底端为重力势能零势能面，一物体在平行于斜面的拉力作用下，由静止开始沿光滑斜面向下运动．运动过程中物体的机械能与物体位移关系的图象（E ﹣x 图象）如图乙所示，其中0～x 1过程的图线为曲线，x 1～x 2过程的图线为直线。

根据该图象，下列判断正确的是A. 0～x 1过程中物体所受拉力可能沿斜面向下B. 0～x 2过程中物体的动能先增大后减小C. x 1～x 2过程中物体做匀加速直线运动D. x 1～x 2过程中物体可能在做匀减速直线运动17．甲乙两球在水平光滑轨道上向同方向运动，已知它们的动量分别是p 1=5 kg·m/s ，p 2=7 kg·m/s ，甲从后面追上乙并发生碰撞，碰后乙球的动量变为10 kg·m/s ，则两球质量与 间的关系可能是下面的哪种A ．B ．C ．D ．18．我国发射的“悟空”探测卫星，三年来对暗物质的观测研究已处于世界领先地位。

**2017—2018学年度高三年级第三次模拟考试**理科数学试卷 第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.已知集合{}{}13,0M x x N x x =-≤<=<，则集合{}03xx ≤<=（ ）A ．MN⋂ B ．MN⋃ C.()R MC N⋂ D ．()R C M N⋂2.复数z 满足()234i z i --=+（i 为虚数单位），则z=（ ）A ．2i -+B ．2i - C. 2i -- D ．2i + 3.已知ta n 16πα⎛⎫+= ⎪⎝⎭，则ta n 6πα⎛⎫-= ⎪⎝⎭（ ）A ．2-．2+C. 2--．2-+4.已知命题:p 在A B C ∆中，若sin sin A B=，则A B=；命题():0,q x π∀∈，1sin 2sin x x+>.则下列命题为真命题的是（ ） A ．pq∧ B ．()pq ∨⌝ C.()()p q ⌝∧⌝ D ．()p q⌝∨5.已知双曲线()2222:10,0x y Ea b ab-=>>的两条渐近线分别为12,l l ，若E 的一个焦点F 关于1l 的对称点F '在2l 上，则E 的离心率为（ ）A B ．326.某几何体的三视图如图所示，则该几何体的体积为（ ）A ．6B ．7 C. 152D ．2337.已知函数()()s in 203f x x πωωω⎛⎫=+-> ⎪⎝⎭的图象与x 轴相切，则()f π=（ ）A ．32-B ．12-12- D ．12--8.已知P 是抛物线24y x=上任意一点，Q 是圆()2241xy-+=上任意一点，则P Q 的最小值为（ ）A ．52B ．1D．19.利用随机模拟的方法可以估计圆周率π的值，为此设计如图所示的程序框图，其中()ra n d 表示产生区间[]0,1上的均匀随机数（实数)，若输出的结果为786，则由此可估计π的近似值为（ ）A ．3.134B ．3.141 C.3.144 D ．3.147 10.在A BC ∆中，点G 满足0G A G BG C ++=.若存在点O ，使得16O GB C=，且O Am O B n O C=+，则m n -=（ ）A ．2B ．2- C. 1 D ．1- 11.若异面直线,m n 所成的角是60︒，则以下三个命题: ①存在直线l ，满足l 与,m n 的夹角都是60︒； ②存在平面α，满足mα⊂，n 与α所成角为60︒；③存在平面,αβ，满足,mn αβ⊂⊂，α与β所成锐二面角为60︒.其中正确命题的个数为（ ）A ．0B ．1 C. 2 D ．3 12.已知()0,xxxea fx e a>=+，若()f x 的最小值为1-，则a=（ ）A ．21eB ．1eC. e D ．2e第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 设变量,x y 满足约束条件10,1,250,x y y x y -+≥⎧⎪≥⎨⎪+-≤⎩则zx y=+的最大值为 ．14.某种袋装大米的质量X （单位：k g ）服从正态分布()50,0.01N ，任意选一袋这种大米，质量在49.850.1kg的概率为 ． 15.设函数()2,0,0,x x f x x ⎧<⎪=≥则使得()()f x fx >-成立的x 得取值范围是 ．16.A B C ∆的内角,,A B C 的对边分别为,,a b c ，角A 的内角平分线交B C 于点D ，若111,2a bc=+=，则A D 的取值范围是 ．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17. 已知数列{}n a 是等差数列，{}n b 是等比数列，111,2a b ==，22337,13a b a b +=+=.（1）求{}n a 和{}n b 的通项公式； （2）若,,n nn a n c b n ⎧⎪=⎨⎪⎩为奇数为偶数，求数列{}n c 的前2n 项和2n S .18. 某球迷为了解,A B 两支球队的攻击能力，从本赛季常规赛中随机调查了20场与这两支球队有关的比赛.两队所得分数分别如下：A球队：122 110 105 105 109 101 107 129 115 100114 118 118 104 93 120 96 102 105 83B球队：114 114 110 108 103 117 93 124 75 10691 81 107 112 107 101 106 120 107 79（1）根据两组数据完成两队所得分数的茎叶图，并通过茎叶图比较两支球队所得分数的平均值及分散程度（不要求计算出具体值，得出结论即可）；（2）根据球队所得分数，将球队的攻击能力从低到高分为三个等级：记事件:C “A 球队的攻击能力等级高于B 球队的攻击能力等级”.假设两支球队的攻击能力相互独立. 根据所给数据，以事件发生的频率作为相应事件发生的概率，求C 的概率. 19.如图，四棱锥PA B C D-的底面A B C D 是平行四边形，90B A CP A D P C D ∠=∠=∠=︒.（1）求证：平面P A B ⊥平面A B C D ；（2）若3AB AC PA ===，E 为B C 的中点，F 为棱P B 上的点，//P D平面A E F ，求二面角A D F E--的余弦值.20.已知点()2,0A -，点()1,0B -，点()1,0C ，动圆O '与x 轴相切于点A ，过点B 的直线1l 与圆O '相切于点D ，过点C 的直线2l 与圆O '相切于点E （,D E 均不同于点A ），且1l 与2l 交于点P ，设点P 的轨迹为曲线Γ. （1）证明：P B P C+为定值，并求Γ的方程；（2）设直线1l 与Γ的另一个交点为Q ，直线C D 与Γ交于,M N两点，当,,O D C '三点共线时，求四边形M P N Q 的面积. 21.已知0a>，函数()24ln 2a f x x x a=+-+.（1）记()()2g a fa =，求()g a 的最小值；（2）若()yfx =有三个不同的零点，求a 的取值范围.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程 已知点A 在椭圆22:24Cx y+=上，将射线O A 绕原点O 逆时针旋转2π，所得射线O B 交直线:2l y =于点B .以O 为极点，x 轴正半轴为极轴建立极坐标系. （1）求椭圆C 和直线l 的极坐标方程；（2）证明：:R t O A B ∆中，斜边A B 上的高h 为定值，并求该定值. 23.选修4-5：不等式选讲 已知函数()123f x x x =---.（1）求不等式()0f x ≥的解集； （2）设()()()g x fx fx =+-，求()g x 的最大值.试卷答案一、选择题1-5: CADBB 6-10: BBDCD 11、12：DA 二、填空题13. 4 14.0.8185 15.()(),10,1?∞-⋃- 16.2⎫⎪⎪⎣⎭三、解答题 17.解：（1）设数列{a n }的公差为d ，数列{b n }的公比为q ， 依题意有，⎩⎨⎧1＋d ＋2q ＝7，1＋2d ＋2q 2＝13，解得d ＝2，q ＝2， 故a n ＝2n －1，b n ＝2n，（2）由已知c 2n －1＝a 2n －1＝4n －3，c 2n ＝b 2n ＝4n， 所以数列{c n }的前2n 项和为S 2n ＝(a 1＋a 3＋…a 2n －1)＋(b 2＋b 4＋…b 2n )＝n(1＋4n －3)2＋4(1－4n)1－4＝2n 2－n ＋ 4 3(4n －1)．18．解：（1）两队所得分数的茎叶图如下3 6 9 3 15 2 4 0 7 1 9 5 5 10 8 367 7 1 6 78 8 4 5 0 11 4 4 0 7 20 9 2 12 4 0通过茎叶图可以看出，A 球队所得分数的平均值高于B 球队所得分数的平均值； A 球队所得分数比较集中，B 球队所得分数比较分散．（2）记C A1表示事件：“A 球队攻击能力等级为较强”， C A2表示事件：“A 球队攻击能力等级为很强”； C B1表示事件：“B 球队攻击能力等级为较弱”， C B2表示事件：“B 球队攻击能力等级为较弱或较强”，则C A1与C B1独立，C A2与C B2独立，C A1与C A2互斥，C ＝(C A1C B1)∪(C A2C B2)． P (C)＝P (C A1C B1)+ P (C A2C B2)＝P (C A1)P (C B1)＋P (C A2)P (C B2)．由所给数据得C A1，C A2，C B1，C B2发生的频率分别为1420，320，520，1820，故P (C A1)＝1420，P (C A2)＝320，P (C B1)＝520，P (C B2)＝1820，P (C)＝1420×520＋320×1820＝0.31．19．解：（1）∵AB ∥CD ，PC ⊥CD ，∴AB ⊥PC ， ∵AB ⊥AC ，AC ∩PC ＝C ，∴AB ⊥平面PAC ， ∴AB ⊥PA ，又∵PA ⊥AD ，AB ∩AD ＝A ， ∴PA ⊥平面ABCD ，PA 平面PAB ， ∴平面PAB ⊥平面ABCD ． （2）连接BD 交AE 于点O ，连接OF ， ∵E 为BC 的中点，BC ∥AD ， ∴ BO OD ＝ BE AD ＝ 1 2， ∵PD ∥平面AEF ，PD 平面PBD ， 平面AEF ∩平面PBD ＝OF ， ∴PD ∥OF ，∴ BF FP ＝ BO OD ＝ 1 2，以AB ，AC ，AP 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系A －xyz ，则A(0，0，0)，B(3，0，0)，C(0，3，0)，D(－3，3，0)， P(0，0，3)，E ( 3 2， 32，0)，F(2，0，1)，设平面ADF 的法向量m ＝(x 1，y 1，z 1)， ∵AF →＝(2，0，1)，AD →＝(－3，3，0)，由AF →·m ＝0，AD →·m ＝0得⎩⎨⎧2x 1＋z 1＝0，－3x 1＋3y 1＝0，取m ＝(1，1，－2)．设平面DEF 的法向量n ＝(x 2，y 2，z 2)，∵DE →＝( 9 2，－ 3 2，0)，EF →＝( 1 2，－ 32，1)，由DE →·n ＝0，EF →·n ＝0得⎩⎨⎧ 9 2x 2－ 32y 2＝0， 1 2x 2－ 32y 2＋z 2＝0，取n ＝(1，3，4)． cos m ，n＝m ·n |m ||n |＝－23939， ∵二面角A-DF-E 为钝二面角，∴二面角A-DF-E 的余弦值为－23939．20．解：（1）由已知可得|PD|＝|PE|，|BA|＝|BD|，|CE|＝|CA|， 所以|PB|＋|PC|＝|PD|＋|DB|＋|PC| ＝|PE|＋|PC|＋|AB| ＝|CE|＋|AB|＝|AC|＋|AB|＝4＞|BC| 所以点P 的轨迹是以B ，C 为焦点的椭圆（去掉与x 轴的交点），可求的方程为x 24＋y23＝1(y ≠0)．（2）由O ，D ，C 三点共线及圆的几何性质，可知PB ⊥CD ， 又由直线CE ，CA 为圆O 的切线，可知CE ＝CA ，O A ＝O E ， 所以△OAC ≌△O EC ，进而有∠ACO ＝∠ECO ，所以|PC|＝|BC|＝2，又由椭圆的定义，|PB|＋|PC|＝4，得|PB|＝2， 所以△PBC 为等边三角形，即点P 在y 轴上，点P 的坐标为(0，±3)(i)当点P 的坐标为(0，3)时，∠PBC ＝60，∠BCD ＝30， 此时直线l 1的方程为y ＝3(x ＋1)，直线CD 的方程为y ＝－33(x －1)， 由⎩⎪⎨⎪⎧x 24＋y 23＝1，y ＝3(x ＋1)整理得5x 2＋8x ＝0，得Q (－ 8 5，－335)，所以|PQ|＝165，由⎩⎪⎨⎪⎧x 24＋y23＝1，y ＝－33(x －1)整理得13x 2－8x －32＝0，设M(x 1，y 1)，N(x 2，y 2)，x 1＋x 2＝813，x 1x 2＝－3213，|MN|＝1＋ 1 3|x 1－x 2|＝4813，所以四边形MPNQ 的面积S ＝1 2|PQ|·|MN|＝38465．(ii)当点P 的坐标为(0，－3)时，由椭圆的对称性，四边形MPNQ 的面积为38465．综上，四边形MPNQ 的面积为38465．21．解：（1）g (a)＝ln a 2＋4a a 2＋a 2－2＝2(ln a ＋ 1 a －1)，g(a)＝2(1a － 1 a )＝2(a －1)a，所以0＜a ＜1时，g (a)＜0，g (a)单调递减；a ＞1时，g(a)＞0，g (a)单调递增，所以g (a)的最小值为g (1)＝0．（2）f(x)＝ 1x －4a (x ＋a 2)2＝x 2＋(2a 2－4a)x ＋a 4x(x ＋a 2)2，x ＞0． 因为y ＝f (x)有三个不同的零点，所以f (x)至少有三个单调区间， 而方程x 2＋(2a 2－4a)x ＋a 4＝0至多有两个不同正根，所以，有⎩⎨⎧2a 2－4a ＜0，Δ＝16a 2(1－a)＞0，解得，0＜a ＜1．由（1）得，当x ≠1时，g (x)＞0，即ln x ＋1x－1＞0， 所以ln x ＞－ 1x，则x ＞e －1x (x ＞0)，令x ＝a 22，得a 22＞e － 2 a 2．因为f (e － 2a 2)＜－ 2 a 2＋ 4 a －2＝－2(a －1)2a2＜0，f (a 2)＞0，f (1)＝4a 1＋a 2－2＝－2(a －1)21＋a 2＜0，f (e 2)＝4a e 2＋a2＞0，所以y ＝f (x)在(e － 2a 2，a 2)，(a 2，1)，(1，e 2)内各有一个零点，故所求a 的范围是0＜a ＜1．22．解：（1）由x ＝ρcos θ，y ＝ρsin θ得椭圆C 极坐标方程为ρ2(cos 2θ＋2sin 2θ)＝4，即ρ2＝41＋sin 2θ； 直线l 的极坐标方程为ρsin θ＝2，即ρ＝ 2sin θ．（2）证明：设A(ρA ，θ)，B (ρB ，θ＋2)，－2＜θ＜ 2．由（1）得|OA|2＝ρ2A ＝41＋sin 2θ，|OB|2＝ρ2B ＝ 4sin 2(θ＋2)＝4cos 2θ， 由S △OAB ＝ 1 2×|OA|×|OB|＝ 12×|AB|×h 可得，h 2＝|OA|2×|OB|2|AB|2＝|OA|2×|OB|2|OA|2＋|OB|2＝2．故h 为定值，且h ＝2．23．解：（1）由题意得|x －1|≥|2x －3|, 所以|x －1|2≥|2x －3|2整理可得3x 2－10x ＋8≤0，解得 4 3≤x ≤2，故原不等式的解集为{x | 43≤x ≤2}．（2）显然g (x)＝f (x)＋f (－x)为偶函数， 所以只研究x≥0时g (x)的最大值．g (x)＝f (x)＋f (－x)＝|x －1|－|2x －3|＋|x ＋1|－|2x ＋3|， 所以x≥0时，g (x)＝|x －1|－|2x －3|－x －2 ＝⎩⎪⎨⎪⎧－4， 0≤x ≤1，2x －6，1＜x ＜ 3 2，－2x ， x ≥ 32，所以当x ＝ 32时，g (x)取得最大值－3，故x ＝± 32时，g (x)取得最大值－3．。

2017 — 2018学年度高三第三次调研测试文科数学本试卷共23小题，共150分，共6页，考试时间120分钟，考试结束后，将答题卡和试 题卷一并交回。

注意事项：1 •答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条 形码、姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。

2.选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案 的标号；非选择题答案必须使用 0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3•请按照题号在各题的答题区域 （黑色线框）内作答，超出答题区域书写的答案无效。

4. 作图可先用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5. 保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮 纸刀。

本大题共 12题，每小题5分，共60分，在每小题给出的四个选项中，只有个是符合题目要求。

设全集 U =Z , A ={-1,1,3,5,7,9}, B ={-1,5,7}，贝V AplG u B)二B. {-1,5,7}D. {-1,1,3,5,9}__nA . -P ： X 。

R,X o 2 乞3X oB . -p: x R,x 22< 3x2C . — p: 一x R,x ■ 2 3xnD . _p: x 0 R,x 0 2 _ 3x 。

2. 已知复数 i z =1—i（i 为虚数单位），则z 的虚部为3.1 .A. i2已知命题P ：X o1 .B.i 2R,x ； 2 3x 0，则命题 1 C.2p 的否命题为D.4. F 列各组向量中，可以作为基底的是A. q =(0,0), e ? =(1,2)B.eiC.e 1 = (3,5), e 2 = (6,10)D.6 = (-1,2),0 = (5,7)、选择题: 1.A. {1,3,9}C.{-1,1,3x - y 3 _ 0设x, y 满足约束条件*x + yZ0，则z = 3x + y 的最小值是x 兰2S n ,则 S n =，定点的坐标是是某几何体的三视图，则该几何体的体积为C. D.5.6. A. -5 B. 4 C. -3D. 11已知等差数列｛务｝的公差不为0,可=1，且32,34,38成等比数列，设｛a n ｝的前n 项和A.n( n 1) 2B.2C. n 2 12 D.n(n 3) 47.以抛物线y 2=8x 上的任意一点为圆心作圆与直线X 二-2相切，这些圆必过一定点，则8. 9. A. (0,2)B. (2, 0)执行如图所示的程序框图，当输出则输入n 的值可以为A.B. C. D.如图，网格纸上小正方形的边长为 C.S =210 时,1,粗实线画出的 (4, 0) D. (0, 4)——n = n - 1否甲S = n ・S(■结束2)A.14二B.310二3 5-J IS = 1C 开始3*/ 输入n // 输岀S /n < 5 ?是俯视图正视图F I +•B 8；侧视图-10.已知锐角：•满足cos( ) =cos2＞，则sin〉cos 等于414 411.朱世杰是历史上最伟大的数学家之一， 他所著的《四元玉鉴》卷中如像招数”五问有如下问题：今有官司差夫一千八百六十四人筑堤•只云初日差六十四人，次日转多七人，每 人日支米三升，共支米四百三石九斗二升， 问筑堤几日”.其大意为：官府陆续派遣1864人前往修筑堤坝，第一天派出 64人，从第二天开始，每天派出的人数比前一天多7人，修筑堤坝的每人每天分发大米3升，共发出大米40392升，问修筑堤坝多少天”.这个问题中， 前5天应发大米12•对于定义域为 R 的函数f(x)，若同时满足下列三个条件：①且 X = 0 时，都有 xf (x)0 ；③当 x 1 ::: 0 x 2，且 I 片 |=| x 2 |时，都有 f (xj ::： f (x 2),则称f(x)为偏对称函数”.现给出下列三个函数：3 3 2 x ] ln(1—x), x 兰 0 f i (x)-X x ； f 2(x) = e - x-1； f 3(x)二212x, x > 0则其中是偏对称函数”的函数个数为 A. 0B. 1C. 2D. 3二、填空题：本大题共 4个小题，每小题5分。

2017~2018 学年度武汉市部分学校九年级调研测试九年级物理试题考试时间为2018 年 1 月26 日一、选择题(只选择一项符合题意的答案字母序号，每小题 3 分，共计36 分)9．扩散现象与人们的生活密切相关。

下列实解中能说明扩散现象对人们有用的是（）A．利用盐水腌制咸鸭蛋B．人造木板粘结剂中的甲醛扩散在空气中C．有人吸烟后房屋中的其他人也能闻到烟味D．将两个底面干净的铅柱压紧后能够吊起重物10．如图所示。

在一个配有活塞的厚玻璃瓶里放一小团硝化棉。

把活塞迅速压下去，硝化棉会燃烧起来。

关于该实验过程，下列说法正确的是（）A．活塞压缩气体做功，筒内气体内能减小B．圧缩过程中气体的内能转化为活塞的机械能C．筒内气体的内能增加主要是因为活塞与筒壁的摩擦造成的D．硝化棉燃烧是因为筒内气体温度升高，达到硝化棉的燃点11．下图是四冲程内燃机某个冲程的示意图。

根出图中活塞和曲轴的位置、进气门和排气门的开闭情况，可以判断该冲程是（）A．吸气冲程B．压缩冲程C．做功冲程D．排气冲程12．下列有关内能的说法正确的是（）A．物体内能增加，温度一定升高B．物体温度升高，内能可能会减少C．物体温度升高，一定是吸收热量D．在热传递过程中，热量可从内能小的物体转移到内能大的物体13．金属锡的原子核带有50 个大小与电子电荷相等的正电荷，关于金属锡的下列说法正确的是（）A．金属锡不能带电B．金属锡导电靠的是原子核内的正电荷C．锡原子核外的电子总共带8×10-18 的电荷D．由于锡原子内既有正电荷，又有负电荷，所以金属锡对外总是显电性14．下列电路图中，与实物电路对应的是（）15．如图所示的电路中，闭合开关后，L1和L2正常发光。

若将手中的两个导线夹接在灯泡L1两端，则出现的现象及其描述正确的是（）A．L1被短接，只有L2发光B．电源被短路，两灯泡都不发光C．电压表能测量出L2两端的电压U2D．L1和L 2两端的电压之和等于3V16．如图所示，a、b 是粗细不同的铜导线，c 是两根连接起来的导线，把它们接入家庭电路中使用时，下列说法正确的是（）A．连接大功率的用电器通常用a 导线B．长度相同时，a、b 两根导线的电阻相等C．c 导线中导线连接处比别处更容易发热D．c 导线中导线连接处电流大于别处电流17．某同学利用如图所示电路进行实验，闭合开关后，L1和L2正常发光，两个电表都有示数。

2019年普通高等学校招生全国统一考试高考模拟调研卷理科数学（三）参考答案一、选择题7～12 DDCDBC6 BCCADA1～f(9?x)?f(7?x)f(6?x)?f(10?x)f(x)?f(6x?)，又得，）题提示：由，第（1210)xf())?f(10?xxf(为周期的周期函数，，即是以?x?3x??13]x)?f(x)f(6?x)f(f(x)[?2，，在上有唯一零点又关于说明对称，而x??1x?78]，?f(x)[2，?在这一个周期内恰有两个零点,?1,9,19,,20092017]?2011,?2001,[?2017，的所有零点为在?10,2007,20173,7,17,,??2013,?2003,的等差数列，，这两列数都是公差为和2009?(?2011)2017?(?2013)?1?403?1?404，且项数分别为和1010(?2011?2009)?403(?2013?2017)?404??405故所有零点之和为22二、填空题56i9（14））（（13）16 ）②③（15?????1?a?01)sin?f()??(a?0?)sin(0,?，?，， 第（16）题提示：由题4????0(0)??cos?f，又，2三、解答题（17）（本小题满分12分）222224S?1?a?2a4a?a?2a?a?2a2a?2a?a?a2)≥(n，（Ⅰ）由题解：，?，1?nnnnn?1nn?1?n?11n??n1n1n2(a?a)?(a?a)(a?a){a}为正项数列，，又数列1nn?n11nn?n?n a?a?2{a}2)(n≥2的等差数列…………………………（，?为公差为3?分）1nn?n21?n1?d?2n1a?a?(n?1)a?1??aa?2a4S?4分），令，解得?6，……………（11n11111111]?b??[分）9（Ⅱ）…………………………（n112n?1)(2n?1)22n?(2n?111111111??))]?(1???[(1?)?(?)?(T分）12?………………（n212n?1n3235?12n?22分））（本小题满分12（18AD??PDPMADMPA?， 解：（Ⅰ）设，中点为CB??PCPNCBNPB 分），?设中点为………………（， 2PMPMNCB?CB/MNMN?CB?CB?ABAB/分），,?……………平面（又,?4,ABCDABCD?PADPM?，平面……………（6?平面分）平面MP,BC,BABz,y,x.为为原点，轴的正方向建立空间直角坐标系（Ⅱ）以点2)P(3,1,(3,1,0)C(0,2,0)D(2,2,0)MA(4,0,0)分），，?……………（，，8),z?(x,ynPAB的法向量为设平面?0x?4?0BA?n???2?z?2)2,n?(0,?分）由，令10，得……………（??0?y?2z?3x?0??BPn????PAB2)??3,1,PC?(PC所成角为与平面，直线，|PC?n|42???sin?分）……………（?123||nPC|?|63?2（19）（本小题满分12分）212203322?)()?C(P?C()分）解：（Ⅰ）该同学至少答对两道基础知识题的概率，……（231327333132?)1?(?P至少答对一道技能题的概率4，……………（分）2425??PP?P分）设同学能够晋级的概率……………（621920555??X(PX?1)?P(?2)?(1?)1,2,3X，可能的取值为，由（（Ⅱ）由题1）得：，8199916?2)(?(?XP(?3)1?PX1)?PX?分）……………（9 8132X116520P8181913352016?EX??2?3???1分）12期望……………（8181819．（20）（本小题满分12分）32222yxxy22?2221?c?c1C:??1C:??1??cba??，，，椭圆（Ⅰ）设椭圆解：，由题，21222222??aabb ba22yx22:C??13b?a?4，，椭圆……………（3分）联立解得134CC的短轴长等于椭圆的长半轴长，椭圆 122x2???1b?2ba??2?2a C1?y:? 5分）?，，，椭圆……………（22xx)y(x,(x,y)PQ11??yl:y分）7 （Ⅱ）设，由替换法则得………（……①，10011AB2 yyyxxxxy)y(x,x,y),BA(BBAA1???1ll::?、设，则BBAAQBQA3443yxxyxxyy)x,yQ(00BA0A0B l,l11????、又在上，?00QBQA3344yxyx001l:???9分）……②………（AB34yxx11001yy?x??x,,?y，即由①②得，010*******22yx21122222??2?2y?x2y?2?x?Q的轨迹为，?12分）又，点………（11009494（21）（本小题满分12分）1?xx)(fxf(x)?1??a?21)?xln(e??e?1?t?0解：（Ⅰ）得时，由，令x1e?11111?0??)??2g?(t1)?g(t)?lnt?ln(t???lnt?ln(t?1)2，即，设2t1tt?tt)tg(所以2单调递增，………（分）111310100?2e??1)?4?0g(eln()?10??g()?lnln?又，，10e222?)(x)?fxf(0)?g(t分）所以有唯一实根………（有唯一解，即方程4xx?a)ee(1?a?(x)??a?f))(0,??f(x………（（Ⅱ）定义域为 5分），xx?11ee?x?1≤≤a00a?)?ae?(1(x)?0f(fx)(0,??)上单调递增；………（，时，，在6当分）a x1?a lnx??0)e??a?0(1?a，时，令当1a?aa)(ln,??)(0,ln)xf(上单调递减；………（?7在上单调递增，在分）1a??1aaa a?0(0,ln)(ln,??))xf(上单调递增；时，同理在………（8在分）当上单调递减，a?1a?111x a?f(x)?lnx?ln(e?1)?x?lnx?0，（Ⅲ）当时，22xxx?e2xe?11xe2?1?x(x)?h???xx?ln?h(x)?ln(e1)?，令xx?1)x2x2(ee?12xxxx?0???2u(x)xe?e1?2xxe)(ux???e0)(uxu()x?(0)u?单调递增，，令，??(x)?0h(hx)单调递增………（10分）?，xxx?e1?e1?11e?x?1ln?0h(x)?ln x?00(x)?h时，，，，，?当x2xx原不等式得证………（12分）（22）（本小题满分10分）2222y?C:x?x?l:y……………（，曲线解：（Ⅰ）直线4分）?2t?x?x?0?2l)y(x,P(t)P…………（，过6平行于的直线的参数方程为为参数分）（Ⅱ）设点?002?y?y?t?02?3222222yC:x??2?2?0x?2?2x22yy)tt??(得：联立曲线0000222|?2?2y|x400?|?|PA|?|PB 9所以分）…………（3322222222y??2|x?2|0xx??2?y2y?4即或，即，00000022l0y?x2?P为原点在直线但上不合题意舍去，时，点00224?2xy?P分）.…………（所以点10轨迹为分）（23）（本小题满分10af(x)≥a≥(x)f…………（2分）解：（Ⅰ） 不等式有解，?max1?≥1,x?2?11??x4x?1,≤?24?)(xf 分） 4，…………（?111??,≤x2x???424?1??≤?1,x4?1≤a1?f(x)，即分）…………（5所以max|m|x)?1≤x?f(（Ⅱ）由题恒成立，1(x)?fy?分）的图象，如下…………（1由（）可得712),(|?mx?y|myx??经过点当函数的一段时，2．3??m满足要求，此时23]?(???,m分）……（结合图象可知，当时满足条件.102．。

2017-2018学年度高三第三次模拟考试(理科)数学试题本试卷共4页，20小题，满分150分．考试用时120分钟 注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上．2．必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．一．选择题(本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．) 1. 已知i z +=1，则2)(z =（ ）A ．2B ．2-C ．i 2D ．i 2- 2. 设全集U=Z ，集合M=}{2,1，P=}{2,1,0,1,2--，则P CuM ⋂=（ ） A ．}{0 B ．}{1 C ．}{0,2,1-- D ．Φ 3. 一枚硬币连掷2次，只有一次出现正面的概率为（ ）A ．32B ．41C ．31D ．214． 已知直线a 、b 、c 和平面M ，则a//b 的一个充分条件是（ ）．A ．a//M ，b//MB ． a ⊥c ，b ⊥cC ．a 、b 与平面M 成等角D ．a ⊥M ，b ⊥M ．5． 已知实数x y 、满足约束条件⎪⎩⎪⎨⎧≤+≥≥622y x y x ，则24z x y =+的最大值为（ ）．A ．24B ．20C ．16D ．12 6．已知向量12||,10||==,且60-=⋅，则向量与的夹角为（ ）A ．060B ．0120C ．0135D ．0150 7．下列命题错误的是（ ）A ．命题“若0m >，则方程20x x m +-=有实根”的逆否命题为：“若方程20x x m +-=无实根，则0m ≤”。

B ．“1x =”是“2320x x -+=”的充分不必要条件。

13题C ．命题“若0xy =，则,x y 中至少有一个为零”的否定是：“若0xy ≠，则,x y 都不为零”。