宁夏银川一中2013届高三上学期第一次月考数学(理)试题

绝密★启用前2013年普通高等学校招生全国统一考试理 科 数 学(银川一中第三次模拟考试)本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第22～24题为选考题，其它题为必考题。

考生作答时，将答案答在答题卡上，在本试卷上答题无效。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。

2．选择题答案使用2B 铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案的标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。

3．请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。

4．保持卡面清洁，不折叠，不破损。

5．做选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。

参考公式：样本数据n x x x ,,21的标准差：222121[()()()]n s x x x x x x n=-+-++-其中x 为样本平均数第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知全集U=R ，设函数y=lg(x-1)的定义域为集合A ，函数y=522++x x 的值域为集合B ，则A∩(C U B)= （ ）A ．[1,2]B ．[1,2)C ．(1,2]D ．(1,2) 2．已知sinθ=54，且sinθ-cosθ>1，则sin2θ= （ ） A ． -2524 B ．-2512 C ．-54 D ．25243．已知等差数列}{n a 满足,0101321=++++a a a a 则有（ ）A ．01011>+a aB ．01002<+a aC ．0993=+a aD ．5151=a4．已知011<<ba ，则下列结论不正确的是（ ）A ．a 2<b 2B ．ab<b 2C ．2>+abb a D ．|a|+|b|>|a+b|5. 下图给出了下一个算法流程图，该算法 流程图的功能是( )A ．求a,b,c 三数的最大数B ．求a,b,c 三数的最小数C ．将a,b,c 按从小到大排列D ．将a,b,c 按从大到小排列6. 已知函数)5(,)0)(3()0(2)(f x x f x x f x则⎪⎩⎪⎨⎧>-≤==（ ） A ．32 B ．16 C ．21 D ．3217. 下列四个命题正确的是（ ） ①正态曲线222)(21)(σμσπ--=x ex f 关于直线x=μ对称；②正态分布N （μ，σ2）在区间（-∞，μ）内取值的概率小于0.5;③服从于正态分布N （μ，σ2）的随机变量在（μ-3σ，μ+3σ）以外取值几乎不可能发生； ④当μ一定时，σ越小，曲线“矮胖” A ．①③B ．②④C ．①④D ．②③？？8．在正方体ABCD--A 1B 1C 1D 1中,M,N 分别为棱AA 1和B 1B 的中点,若θ为直线CM 与D 1N 所成的角,则sin θ= ( ) A ．91 B. 32C. 952D. 9549．函数y=sinxcosx+3cos 32-x 的图象的一个对称中心是（ ） A )23,32(-π B )23,65(-π C )23,32(π- D )3,3(-π10．甲、乙两棉农，统计连续五年的面积产量(千克∕亩)如下表：棉农甲 68 72 70 69 71 棉农乙6971686869则平均产量较高与产量较稳定的分别是（ ） A ．棉农甲，棉农甲B ．棉农甲，棉农乙C ．棉农乙，棉农甲D ．棉农乙，棉农乙11. 已知函数34)(2+-=x x x f ，集合(){}0)()(,≤+=y f x f y x M ， 集合(){}0)()(,≥-=y f x f y x N ，则集合N M 的面积是（ ）A ．4πB ．2πC ．πD ．π212．设f (x )，g (x )分别是定义在R 上的奇函数和偶函数，当x <0时，0)(')()()('>+x g x f x g x f ，且0)3(=-f ，则不等式0)()(<x g x f 的解集是( ）A ．(－3，0)∪(3，+∞)B ．(－3，0)∪(0，3)C ．(－∞，－3)∪(3，+∞)D ．(－∞，－3)∪(0，3)第Ⅱ卷本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第24题为选考题，考生根据要求做答． 二、填空题：本大题共4小题，每小题5分．13. 椭圆19822=++y k x 的离心率为21，则k 的值为________.14. 已知函数),(1222)(R x a a x f x x ∈+-+⋅=是奇函数，则实数a 的值________. 15. 已知边长分别为a 、b 、c 的三角形ABC 面积为S ，内切圆O 半径为r ，连接OA 、OB 、OC ，则三角形OAB 、OBC 、OAC 的面积分别为21cr 、21ar 、21br ，由S=21cr+21ar+21br 得r=cb a S++2，类比得若四面体的体积为V,四个面的面积分别为A 、B 、C 、D ，则内切球的半径R=_____________.16.若数列}{n a 满足}*1112()1nn n na a a n N a ++==∈-数列满足，，则该数列的前2013项的乘积______.三、解答题:本大题共5小题，共计70分。

宁夏银川一中2013届高三上学期第三次月考数学（文）试卷第Ⅰ卷一、选择题（本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.） 1．集合，,则下列结论正确的是( )A. B.C.D.2．已知n S 为等差数列{}n a 的前n 项的和，254a a +=，721S =，则7a 的值为( )A ．6B ．7C ．8D ． 93．已知向量(cos ,2),(sin ,1),//a b a b αα=-=则tan()4πα-等于( )A ．3 B.3- C. 13 D. 13- 4．已知平面向量,m n 的夹角为,6π23==，在ABC ∆中，22AB m n =+，26AC m n =-，D 为BC 中点，则AD =( )A.2B.4C.6D.85．已知向量(1,2),(1,),a b a b b λ==-+若与垂直，则实数λ的值为( ) A ．-2或0 B ．-2或12 C ．-2 D ．126．如图，设A 、B 两点在河的两岸， 一测量者在A 的同侧所在的 河岸边选定一点C ，测出AC 的距离为50m ，∠ACB =45o, ∠CAB =105o后，就可以计算出A 、B 两点的距离为( )A.B.B.D.2m 7. 已知各项均为正数的等比数列{}n a 中，13213a ,a ,2a 2成等差数列，则1113810a a a a +=+( ) A. 1-或3 B. 3 C. 27D. 1或278．如果22)4sin(2cos -=-παx ，则ααsin cos +的值为( ) A ．27-B ．21-C ．21D ．279. 如右图,在△ABC 中,13AN NC −−→−−→=,P 是BN 上的一点,若29AP m AB AC −−→−−→−−→=+,则实数m 的值为( )A.19 B 31C. 1D. 3 10．给出下列各函数值：①sin(-10000) ②cos(-22000) ③tan(-10) ④917tancos 107sinπππ其中符号为负的有( ) A ．①B ．②C ．③D ． ④11．已知直线212(),0,3()11,02x x y mx y f x x x ⎧-≤⎪⎪===⎨⎪+>⎪⎩与函数的图象恰好有3个不同的公共点，则实数m 的取值范围是( )A．4)B．)+∞C．D．11．已知定义在R 上的奇函数)(x f 和偶函数)(x g 满足,0(2)()(>+-=+-a a a x g x f x x 且)1≠a ，若a g =)2(，则)2(f = ( ) A. 2 B.417 C. 415D. 2a 第Ⅱ卷本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第24题为选考题，考生根据要求做答．二、填空题（本大题共4小题，每小题5分，共20分，将答案填在答题卡相应的位置上．） 13. 在△ABC 中，若1=b ,3=c , 32π=∠C ,则______=∆ABC S . 14．向量(3,4)a =在向量(1,0)b =方向上的投影为__________.15. 已知向量=(3，-4),=(6，-3),=(5-M ，－３－ｍ)若∠ＡＢＣ为锐角，则实数ｍ的取值范围是__________.16．设函数c bx x x x f ++=)(,给出以下四个命题：①当c =0时，有成立；)()(x f x f -=-②当b =0,c>0时，方程只有一个实数根；,0)(=x f ③函数)(x f y =的图象关于点（0，c ）对称 ④当x>0时；函数c bx x x x f ++=)(，2)(2b c x f -有最小值是。

九年上元堂Unit 3 Period 5 （Integrated skills） 一、词组翻译 1． _________________________2． _______________ 3．____________________4． _________________________ 5． ______________________ 6． _____________________________ 7． ______________________________8． _______________________________ 二、词汇运用 1. Please read the letter ____________ (大声) so that everybody can hear you. 2.Kate is so clever. She always answers questions ____________ (correct) . 3. As a new Grade 9 student, he is interested in _________________(化学）. 4. Can you pay more a___________ to your spelling? 5. He often comes here to check on my _____________(进步). 6. I don’t know how to______________(发音) this word. That is to say I don’t know the____________(发音) of this word. 7. Thanks for s___________ your experiences with me. 8. All his s are valuable to our study. It’s better for us to take his advice. 三、单项选择。

宁夏银川一中2013届高三上学期第五次月考数学（文）试题2012.12第Ⅰ卷一、选择题（本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．设集合M ＝{－1,0,1}，N ＝{x |x 2≤x }，则M ∩N ＝( ) A ．{0} B ．{0,1} C ．{－1,1} D ．{－1,0,1} 2．命题p ：0∀>x ，都有sinx ≥-1，则( )A ．p ⌝：0∃>x ，使得sin 1x <- B. p ⌝：0∀>x ，都有sinx<-1 C. p ⌝：0∃>x ，使得sin 1x >- D. p ⌝：0x ∀>，都有sinx ≥-1 3．已知向量)0,3(),1,2(-=-=b a ，则a 在b 方向上的投影为( )A ．5-B ．5C ．-2D ．24．在等差数列{a n }中，已知a 4＋a 8＝16，则a 2＋a 10＝（ ） A.12 B.16 C.20 D.245. 设a ∈R ，则“a ＝1”是“直线l 1：ax ＋2y －1＝0与直线l 2：x ＋(a ＋1)y ＋4＝0平行”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 6．同时具有性质：①最小正周期是π；②图像关于直线3π=x 对称；③在]3,6[ππ-上是增函数的一个函数是（ ） A ．)62sin(π+=x y B ．)32cos(π+=x yC ．)62sin(π-=x yD ．cos()26x y π=-7．双曲线)0(122≠=-mn nymx的离心率为2，有一个焦点与抛物线x y42=的焦点重合，则mn 的值为（ ） A ．38 B ．83 C ．316 D ．1638．已知函数32()22f x x x =-+有唯一零点，则下列区间必存在零点的是( ) A ．3(2,)2--B ．3(,1)2-- C ．1(1,)2--D ．1(,0)2-9. 与直线04=--y x 和圆02222=-++y x y x 都相切的半径最小的圆的方程是( ) A. 22(1)(1)2x y +++= B. 22(1)(1)4x y +++= C. 2)1()1(22=++-y x D. 4)1()1(22=++-y x 10. 已知)(x f ，)(x g 都是定义在R 上的函数，且满足以下条件：①)(x f =x a 〃)(x g （1,0≠>a a ）；②)(x g 0≠； ③)()()()(x g x f x g x f ⋅'>'⋅； 若25)1()1()1()1(=--+g f g f ，则a 等于( )A ．21 B ．2 C ．45D ．2或2111．已知()2sin(+)f x x ωϕ= , (ω>0 , 22πϕπ<<-) ， A 、B 为图象上两点，B 是图象的最高点，C 为B 在x 轴上射影，且点C 的坐标为),0,12(π则AB 〃BC =( ).A.4π4+ B.4π4-C. 4D. 4-12.已知定义在R 上的奇函数()f x 满足()()4f x f x -=-，且[]0,2x ∈时，()()2log 1f x x =+，甲，乙，丙，丁四位同学有下列结论：甲：()31f =；乙：函数()f x 在[]6,2--上是增函数；丙：函数()f x 关于直线4x =对称；丁：若()0,1m ∈，则关于x 的方程()0f x m -=在[]8,8-上所有根之和为-8，其中正确的是（ ）A.甲，乙,丁B.乙,丙C.甲,乙,丙D.甲,丁第Ⅱ卷本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第24题为选考题，考生根据要求做答．二、填空题（本大题共4小题，每小题5分，共20分，将答案填在答题卡相应的位置上．） 13．已知圆x 2＋y 2－6x －7＝0与抛物线y 2＝2px （p >0）的准线相切，则此抛物线的焦点坐标是___________。

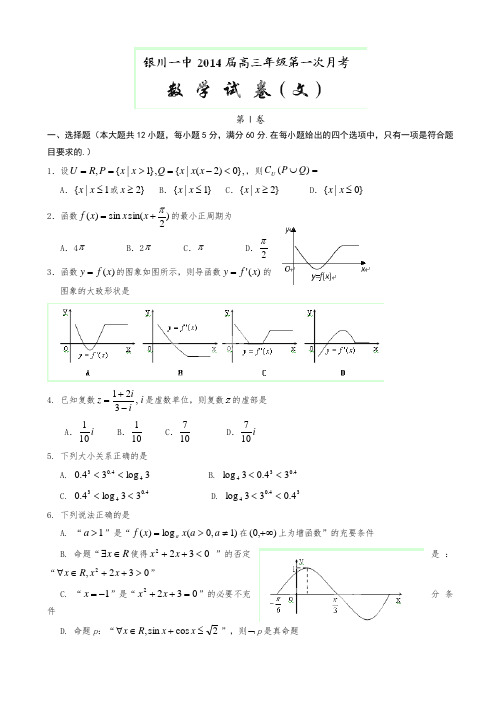
第Ⅰ卷一、选择题（本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．设},0)2(|{},1|{,<-=>==x x x Q x x P R U ，则=⋃)(Q P C UA ．1|{≤x x 或}2≥xB ．}1|{≤x xC ．}2|{≥x xD ．}0|{≤x x 2．函数)2sin(sin )(π+=x x x f 的最小正周期为A ．4πB ．2πC ．πD ．2π 3．函数)(x f y =的图象如图所示，则导函数)('x f y =的 图象的大致形状是4. 已知复数,321iiz -+=i 是虚数单位，则复数的虚部是 A ．i 101 B ．101 C ．107D ．i 1075. 下列大小关系正确的是 A. 3log 34.044.03<< B. 4.03434.03log <<C. 4.04333log 4.0<< D. 34.044.033log <<6. 下列说法正确的是 A. “1>a ”是“)1,0(log )(≠>=a a x x f a 在),0(+∞上为增函数”的充要条件 B. 命题“R x ∈∃使得0322<++x x ”的否定是：“032,2>++∈∀x x R x ”C. “1-=x ”是“0322=++x x ”的必要不充分条件D. 命题p ：“2cos sin ,≤+∈∀x x R x ”，则⌝p 是真命题7. 函数)2||,0)(sin()(πϕωϕω<>+=x x f 的部分图像如图所示，如果)3,6(,21ππ-∈x x ，且)()(21x f x f =， 则=+)(21x x f A ．21B ．22C ．23D ．18. 已知),0(πα∈，且,21cos sin =+αα则α2cos 的值为A ．47±B ．47C ．47-D ．43- 9. 函数ax x x f +=ln )(存在与直线02=-y x 平行的切线，则实数a 的取值范围是A. ]2,(-∞B. )2,(-∞C. ),2(+∞D. ),0(+∞ 10. 已知函数)2cos()(ϕ+=x x f 满足)1()(f x f ≤对R x ∈恒成立，则A. 函数)1(+x f 一定是偶函数B.函数)1(-x f 一定是偶函数C. 函数)1(+x f 一定是奇函数D.函数)1(-x f 一定是奇函数11. 已知函数),1,0(,,ln )(21ex x x x f ∈=且21x x <则下列结论正确的是 A ．0)]()()[(2121<--x f x f x x B ．2)()()2(2121x f x f x x f +<+C ．)()(1221x f x x f x >D ．)()(1122x f x x f x >12. 已知函数)(x f 满足)()1(x f x f -=+，且)(x f 是偶函数，当]1,0[∈x 时， 2)(x x f =，若在区间[-1,3]内，函数k kx x f x g --=)()(有4个零点，则实数的取值范围是 A ．)31,41[B ．)21,0(C ．]41,0(D ．)21,31(第Ⅱ卷本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第24题为选考题，考生根据要求做答． 二、填空题：本大题共4小题，每小题5分．13. 已知函数x a x f 2log )(-=的图象经过点A (1,1)，则不等式1)(>x f 的解集为______.14. 已知α为钝角，且53)2cos(-=+απ，则 。

2015-2016学年宁夏银川一中高三（上）第一次月考数学试卷（理科）一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A={x|x＞1}，B={0，1，2，4}，则（C R A）∩B=（）A．{0，1} B．{0} C．{2，4} D．∅2．下列命题中是假命题的是（）A．∀x∈R，2x﹣1＞0 B．∀x∈N﹡，（x﹣1）2＞0 C．∃x∈R，lgx＜1 D．∃x∈R，tanx=2 3．，则m等于（）A．﹣1 B．0 C．1 D．24．下列函数中，既是偶函数，又在区间（1，2）内是增函数的为（）A．y=cos2x B．y=log2|x| C．D．y=x3+15．若tanθ+=4，则sin2θ=（）A．B．C．D．6．若x∈（0，1），则下列结论正确的是（）A．B．C．D．7．已知P、Q是圆心在坐标原点O的单位圆上的两点，分别位于第一象限和第四象限，且P点的纵坐标为，Q点的横坐标为．则cos∠POQ=（）A．B．C．﹣D．﹣8．现有四个函数：①y=x•sinx；②y=x•cosx；③y=x•|cosx|；④y=x•2x的图象（部分）如下：则按照从左到右图象对应的函数序号安排正确的一组是（）A．①④③② B．③④②① C．④①②③ D．①④②③9．设函数，其中，则导数f′（﹣1）的取值范围（）A．[3，6] B．C．D．10．函数的图象与x轴的交点的横坐标构成一个公差为的等差数列，要得到函数g（x）=Acosωx的图象，只需将f（x）的图象（）A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位11．若函数f（x）满足，当x∈[0，1]时，f（x）=x，若在区间（﹣1，1]上，g（x）=f（x）﹣mx﹣m有两个零点，则实数m的取值范围是（）A．B．C．（0，1）D．12．设函数，且αsinα﹣βsinβ＞0，则下列不等式必定成立的是（）A．α＞βB．α＜βC．α+β＞0 D．α2＞β2二、填空题：本大题共4小题，每小题5分，共20分.13．如图，某港口一天6时到18时的水渠变化曲线近似满足函数y=3sin（x+φ）+k．据此函数可知，这段时间水深（单位：m）的最大值为．14．已知，，则= ．15．已知点P在曲线y=上，a为曲线在点P处的切线的倾斜角，则a的取值范围是．16．给出下列四个命题：①半径为2，圆心角的弧度数为的扇形面积为②若α，β为锐角，，则③是函数y=sin（2x+φ）为偶函数的一个充分不必要条件④函数的一条对称轴是其中正确的命题是．三、解答题：解答应写出文字说明，证明过程或演算步骤.17．（12分）（2015秋•乌拉特前旗校级月考）某同学用五点法画函数f（x）=Asin（ωx+ϕ），（ω＞0，|ϕ|＜）在某一个周期内的图象时，列表并填入了部分数据，如下表：ωx+ϕ0 π2πxAsin（ωx+ϕ）0 5 ﹣5 0（1）请将上表数据补充完整，并直接写出函数f（x）的解析式；（2）若函数f（x）的图象向左平移个单位后对应的函数为g（x），求g（x）的图象离原点最近的对称中心．18．（12分）（2014•江西）已知函数f（x）=（a+2cos2x）cos（2x+θ）为奇函数，且f（）=0，其中a∈R，θ∈（0，π）．（1）求a，θ的值；（2）若f（）=﹣，α∈（，π），求sin（α+）的值．19．（12分）（2012•佛山二模）某种产品每件成本为6元，每件售价为x元（x＞6），年销量为u万件，若已知与成正比，且售价为10元时，年销量为28万件．（1）求年销售利润y关于x的函数关系式．（2）求售价为多少时，年利润最大，并求出最大年利润．20．（12分）（2014•天津模拟）已知函数f（x）=x3﹣3ax2+b（x∈R），其中a≠0，b∈R．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）设a∈[，]，函数f（x）在区间[1，2]上的最大值为M，最小值为m，求M﹣m的取值范围．21．（12分）（2015•大观区校级四模）已知函数f（x）=ax+xlnx（a∈R）（1）若函数f（x）在区间[e，+∞）上为增函数，求a的取值范围；（2）当a=1且k∈z时，不等式k（x﹣1）＜f（x）在x∈（1，+∞）上恒成立，求k的最大值．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.答时用2B 铅笔在答题卡上把所选题目的题号涂黑.选修4-1：几何证明选讲22．（10分）（2015•金昌校级模拟）如图，AB是⊙O的一条切线，切点为B，ADE、CFD都是⊙O 的割线，AC=AB，CE交⊙O于点G．（Ⅰ）证明：AC2=AD•AE；（Ⅱ）证明：FG∥AC．选修4-4：坐标系与参数方程23．（2015•鹰潭一模）选修4﹣4：坐标系与参数方程．极坐标系与直角坐标系xoy有相同的长度单位，以原点为极点，以x轴正半轴为极轴，已知曲线C1的极坐标方程为ρ=4cosθ，曲线C2的参数方程为（t为参数，0≤α＜π），射线θ=φ，θ=φ+，θ=φ﹣与曲线C1交于（不包括极点O）三点A、B、C．（I）求证：|OB|+|OC|=|OA|；（Ⅱ）当φ=时，B，C两点在曲线C2上，求m与α的值．选修4-5：不等式选讲24．（2015•鹰潭一模）已知函数f（x）=|x+2|﹣2|x﹣1|（1）解不等式f（x）≥﹣2；（2）对任意x∈[a，+∞），都有f（x）≤x﹣a成立，求实数a的取值范围．2015-2016学年宁夏银川一中高三（上）第一次月考数学试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A={x|x＞1}，B={0，1，2，4}，则（C R A）∩B=（）A．{0，1} B．{0} C．{2，4} D．∅考点：交、并、补集的混合运算．专题：计算题．分析：由集合A={x|x＞1}，B={0，1，2，4}，知C R A={x≤1}，由此能求出（C R A）∩B．解答：解：∵集合A={x|x＞1}，B={0，1，2，4}，∴C R A={x≤1}，∴（C R A）∩B={0，1}．故选A．点评：本题考查集合的交、并、补集的混合运算，是基础题．解题时要认真审题，仔细解答．2．下列命题中是假命题的是（）A．∀x∈R，2x﹣1＞0 B．∀x∈N﹡，（x﹣1）2＞0 C．∃x∈R，lgx＜1 D．∃x∈R，tanx=2 考点：四种命题的真假关系．专题：简易逻辑．分析：本题考查全称命题和特称命题真假的判断，逐一判断即可．解答：解：B中，x=1时不成立，故选B．答案：B．点评：本题考查逻辑语言与指数函数、二次函数、对数函数、正切函数的值域，属容易题．3．，则m等于（）A．﹣1 B．0 C．1 D．2考点：定积分．专题：导数的概念及应用．分析：利用定积分的几何意义计算定积分．解答：解：y=，即（x+1）2+y2=1，表示以（﹣1，0）为圆心，以1为半径的圆，圆的面积为π，∵，∴表示为圆的面积的二分之一，∴m=0，故选：B点评：本题主要考查定积分、定积分的几何意义、圆的面积等基础知识，考查考查数形结合思想．属于基础题．4．下列函数中，既是偶函数，又在区间（1，2）内是增函数的为（）A．y=cos2x B．y=log2|x| C．D．y=x3+1考点：奇偶性与单调性的综合．专题：函数的性质及应用．分析：利用函数奇偶性的定义及基本函数的单调性可作出判断．解答：解：函数y=log2|x|的定义域为（﹣∞，0）∪（0，+∞），关于原点对称，且log2|﹣x|=log2|x|，∴函数y=log2|x|为偶函数，当x＞0时，函数y=log2|x|=log2x为R上的增函数，所以在（1，2）上也为增函数，故选B．点评：本题考查函数的奇偶性、单调性，属基础题，定义是解决该类题目的基本方法．5．若tanθ+=4，则sin2θ=（）A．B．C．D．考点：二倍角的正弦；同角三角函数间的基本关系．专题：三角函数的求值．分析：先利用正弦的二倍角公式变形，然后除以1，将1用同角三角函数关系代换，利用齐次式的方法化简，可求出所求．解答：解：sin2θ=2sinθcosθ=====故选D．点评：本题主要考查了二倍角公式，以及齐次式的应用，同时考查了计算能力，属于基础题．6．若x∈（0，1），则下列结论正确的是（）A．B．C．D．考点：不等式比较大小．专题：不等式．分析：根据指数函数幂函数对数函数的图象与性质，得到不等式与0，1的关系，即可比较大小．解答：解：x∈（0，1），∴lgx＜0，2x＞1，0＜＜1，∴2x＞＞lgx，故选：C．点评：本题考查了不等式的大小比较，以及指数函数幂函数对数函数的图象与性质，属于基础题．7．已知P、Q是圆心在坐标原点O的单位圆上的两点，分别位于第一象限和第四象限，且P点的纵坐标为，Q点的横坐标为．则cos∠POQ=（）A．B．C．﹣D．﹣考点：两角和与差的余弦函数；任意角的三角函数的定义．专题：三角函数的求值．分析：由条件利用直角三角形中的边角关系求得sin∠xOP和cos∠xOQ的值，利用同角三角函数的基本关系求得cos∠xOP 和sin∠xOQ，再利用两角和的余弦公式求得cos∠POQ=cos（∠xOP+∠xOQ ）的值．解答：解：由题意可得，sin∠xOP=，∴cos∠xOP=；再根据cos∠xOQ=，可得sin∠xOQ=．∴cos∠POQ=cos（∠xOP+∠xOQ ）=cos∠xOP•cos∠xOQ﹣sin∠xOP•sin∠xOQ=﹣=﹣，故选：D．点评：本题主要考查直角三角形中的边角关系，同角三角函数的基本关系，两角和的余弦公式的应用，属于基础题．8．现有四个函数：①y=x•sinx；②y=x•cosx；③y=x•|cosx|；④y=x•2x的图象（部分）如下：则按照从左到右图象对应的函数序号安排正确的一组是（）A．①④③② B．③④②① C．④①②③ D．①④②③考点：函数的图象．专题：函数的性质及应用．分析：从左到右依次分析四个图象可知，第一个图象关于Y轴对称，是一个偶函数，第二个图象不关于原点对称，也不关于Y轴对称，是一个非奇非偶函数；第三、四个图象关于原点对称，是奇函数，但第四个图象在Y轴左侧，图象都在x轴的下方，再结合函数的解析式，进而得到答案．解答：解：分析函数的解析式，可得：①y=x•sinx为偶函数；②y=x•cosx为奇函数；③y=x•|cosx|为奇函数，④y=x•2x为非奇非偶函数且当x＜0时，③y=x•|cosx|≤0恒成立；则从左到右图象对应的函数序号应为：①④②③故选：D．点评：本题考点是考查了函数图象及函数图象变化的特点，解决此类问题有借助两个方面的知识进行研究，一是函数的性质，二是函数图象要过的特殊点．9．设函数，其中，则导数f′（﹣1）的取值范围（）A．[3，6] B．C．D．考点：三角函数中的恒等变换应用；函数的值域．分析：先对原函数进行求导可得到f′（x）的解析式，将x=﹣1代入可求取值范围．解答：解：∵∴∴=2sin（）+4∵∴∴s in∴f′（﹣1）∈[3，6]故选A．点评：本题主要考查函数求导和三角函数求值域的问题．这两个方面都是高考中必考内容，难度不大．10．函数的图象与x轴的交点的横坐标构成一个公差为的等差数列，要得到函数g（x）=Acosωx的图象，只需将f（x）的图象（）A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：由题意可得，函数的周期为π，由此求得ω=2，由g（x）=Acosωx=sin[2（x+）+]，根据y=Asin（ωx+∅）的图象变换规律得出结论．解答：解：由题意可得，函数的周期为π，故=π，∴ω=2．要得到函数g（x）=Acosωx=sin[2（x+）+]的图象，只需将f（x）=的图象向左平移个单位即可，故选A．点评：本题主要考查y=Asin（ωx+∅）的图象变换规律，y=Asin（ωx+∅）的周期性，属于中档题．11．若函数f（x）满足，当x∈[0，1]时，f（x）=x，若在区间（﹣1，1]上，g（x）=f（x）﹣mx﹣m有两个零点，则实数m的取值范围是（）A．B．C．（0，1）D．考点：函数零点的判定定理．专题：函数的性质及应用．分析：根据函数f（x）满足，当x∈[0，1]时，f（x）=x，求出x∈（﹣1，0）时，f（x）的解析式，由在区间（﹣1，1]上，g（x）=f（x）﹣mx﹣m有两个零点，转化为两函数图象的交点，利用图象直接的结论．解答：解：函数f（x）满足，当x∈[0，1]时，f（x）=x，∴x∈（﹣1，0）时，f（x）+1==，f（x）=．因为g（x）=f（x）﹣mx﹣m有两个零点，所以y=f（x）与y=mx+m的图象有两个交点，函数图象如图所示，由图象可得，当0＜m≤时，两函数有两个交点，故选 D．点评：此题是个中档题．本题考查了利用函数零点的存在性求变量的取值范围和代入法求函数解析式，体现了转化的思想，以及利用函数图象解决问题的能力，体现了数形结合的思想．也考查了学生创造性分析解决问题的能力，属于中档题．12．设函数，且αsinα﹣βsinβ＞0，则下列不等式必定成立的是（）A．α＞βB．α＜βC．α+β＞0 D．α2＞β2考点：正弦函数的单调性．专题：综合题．分析：构造函数f（x）=xsinx，x∈，利用奇偶函数的定义可判断其奇偶性，利用f′（x）=sinx+xcosx可判断f（x）=xsinx，x∈[0，]与x∈[﹣，0]上的单调性，从而可选出正确答案．解答：解：令f（x）=xsinx，x∈，∵f（﹣x）=﹣x•sin（﹣x）=x•sinx=f（x），∴f（x）=xsinx，x∈为偶函数．又f′（x）=sinx+xcosx，∴当x∈[0，]，f′（x）＞0，即f（x）=xsinx在x∈[0，]单调递增；同理可证偶函数f（x）=xsinx在x∈[﹣，0]单调递减；∴当0≤|β|＜|α|≤时，f（α）＞f（β），即αsinα﹣βsinβ＞0，反之也成立；故选D．点评：本题考查正弦函数的单调性，难点在于构造函数f（x）=xsinx，x∈，通过研究函数f（x）=xsinx，的奇偶性与单调性解决问题，属于难题．二、填空题：本大题共4小题，每小题5分，共20分.13．如图，某港口一天6时到18时的水渠变化曲线近似满足函数y=3sin（x+φ）+k．据此函数可知，这段时间水深（单位：m）的最大值为8 ．考点：由y=Asin（ωx+φ）的部分图象确定其解析式．专题：三角函数的图像与性质．分析：由图象观察可得：y min=﹣3+k=2，从而可求k的值，从而可求y max=3+k=3+5=8．解答：解：∵由题意可得：y min=﹣3+k=2，∴可解得：k=5，∴y max=3+k=3+5=8，故答案为：8．点评：本题主要考查了正弦函数的图象和性质，属于基本知识的考查．14．已知，，则= ．考点：两角和与差的正切函数．专题：计算题；三角函数的求值．分析：利用辅助角公式sinα+cosα=sin（α+），可求得sin（α+），结合α的范围，可α+∈（，），利用同角的三角函数关系可求cos（α+），tan（α+）的值．解答：解：∵sinα+cosα=sin（α+）=﹣，∴sin（α+）=﹣，∵α∈（，π），∴α+∈（，），∴cos（α+）=﹣=﹣．∴tan（α+）==．故答案为：．点评：本题考查同角三角函数间的基本关系，考查了计算能力，属于基础题．15．已知点P在曲线y=上，a为曲线在点P处的切线的倾斜角，则a的取值范围是．考点：导数的几何意义．专题：计算题；数形结合．分析：由导函数的几何意义可知函数图象在切点处的切线的斜率值即为其点的导函数值，结合函数的值域的求法利用基本不等式求出k的范围，再根据k=tanα，结合正切函数的图象求出角α的范围．解答：解：根据题意得f′（x）=﹣，∵，且k＜0则曲线y=f（x）上切点处的切线的斜率k≥﹣1，又∵k=tanα，结合正切函数的图象由图可得α∈，故答案为：．点评：本题考查了导数的几何意义，以及利用正切函数的图象求倾斜角等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．16．给出下列四个命题：①半径为2，圆心角的弧度数为的扇形面积为②若α，β为锐角，，则③是函数y=sin（2x+φ）为偶函数的一个充分不必要条件④函数的一条对称轴是其中正确的命题是②③④．考点：命题的真假判断与应用；两角和与差的正切函数．专题：三角函数的图像与性质．分析：①利用弧度制的定义可得公式：s扇形=Lr，L=αr，求解即可；②tan（α+2β）=tan（α+β+β）==1，再判断α+2β＜180°，得出答案；③考查了周期函数，+2kπ都能使函数y=sin（2x+φ）为偶函数，④考查三角函数对称轴的特征：过余弦函数的最值点都是对称轴，把代入得：y=cosπ=﹣1，是对称轴，解答：解：①s扇形=Lr，L=αr∴s=1，故错误；②tan（α+2β）=tan（α+β+β）==1∵α，β为锐角，，∴α+2β＜180°∴，故②正确；③+2kπ都能使函数y=sin（2x+φ）为偶函数，故③正确；④把代入得：y=cosπ=﹣1，是对称轴，故正确；故答案为：②③④．点评：考查了弧度制的定义和三角函数的周期性，对称轴和和角公式，属于基础题型，应熟练掌握．三、解答题：解答应写出文字说明，证明过程或演算步骤.17．（12分）（2015秋•乌拉特前旗校级月考）某同学用五点法画函数f（x）=Asin（ωx+ϕ），（ω＞0，|ϕ|＜）在某一个周期内的图象时，列表并填入了部分数据，如下表：ωx+ϕ0 π2πxAsin（ωx+ϕ）0 5 ﹣5 0（1）请将上表数据补充完整，并直接写出函数f（x）的解析式；（2）若函数f（x）的图象向左平移个单位后对应的函数为g（x），求g（x）的图象离原点最近的对称中心．考点：由y=Asin（ωx+φ）的部分图象确定其解析式；函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：（1）由表中已知数据易得，可得表格和解析式；（2）由函数图象变换可得g （x ）的解析式，可得对称中心． 解答： 解：（1）根据表中已知数据，解得数据补全如下表：ωx+ϕ 0 π2πxAsin （ωx+ϕ） 0 5 0 ﹣5 0 ∴函数的解析式为；（2）函数f （x ）图象向左平移个单位后对应的函数是g （x ）=5sin[2（x+）﹣]=5sin （2x+）， 其对称中心的横坐标满足2x+=k π，即x=﹣，k ∈Z ，∴离原点最近的对称中心是点评： 本题考查三角函数解析式的确定和函数图象变换，涉及三角函数的对称性，属基础题．18．（12分）（2014•江西）已知函数f （x ）=（a+2cos 2x ）cos （2x+θ）为奇函数，且f （）=0，其中a ∈R ，θ∈（0，π）． （1）求a ，θ的值； （2）若f （）=﹣，α∈（，π），求sin （α+）的值．考点： 三角函数中的恒等变换应用；函数奇偶性的性质． 专题： 三角函数的求值． 分析： （1）把x=代入函数解析式可求得a 的值，进而根据函数为奇函数推断出f （0）=0，进而求得cos θ，则θ的值可得． （2）利用f （）=﹣和函数的解析式可求得sin，进而求得cos，进而利用二倍角公式分别求得sin α，cos α，最后利用两角和与差的正弦公式求得答案． 解答： 解：（1）f （）=﹣（a+1）sin θ=0，∵θ∈（0，π）． ∴sin θ≠0，∴a+1=0，即a=﹣1 ∵f（x ）为奇函数，∴f（0）=（a+2）cos θ=0，∴cosθ=0，θ=．（2）由（1）知f（x）=（﹣1+2cos2x）cos（2x+）=cos2x•（﹣sin2x）=﹣，∴f（）=﹣sinα=﹣，∴sinα=，∵α∈（，π），∴cosα==﹣，∴sin（α+）=sinαcos+cosαsin=．点评：本题主要考查了同角三角函数关系，三角函数恒等变换的应用，函数奇偶性问题．综合运用了所学知识解决问题的能力．19．（12分）（2012•佛山二模）某种产品每件成本为6元，每件售价为x元（x＞6），年销量为u万件，若已知与成正比，且售价为10元时，年销量为28万件．（1）求年销售利润y关于x的函数关系式．（2）求售价为多少时，年利润最大，并求出最大年利润．考点：函数模型的选择与应用．专题：应用题．分析：（1）根据题中条件：“若已知与成正比”可设，再依据售价为10元时，年销量为28万件求得k值，从而得出年销售利润y关于x的函数关系式．（2）利用导数研究函数的最值，先求出y的导数，根据y′＞0求得的区间是单调增区间，y′＜0求得的区间是单调减区间，从而求出极值进而得出最值即可．解答：解：（1）设，∵售价为10元时，年销量为28万件；∴，解得k=2．∴=﹣2x2+21x+18．∴y=（﹣2x2+21x+18）（x﹣6）=﹣2x3+33x2﹣108x﹣108．（2）y'=﹣6x2+66x﹣108=﹣6（x2﹣11x+18）=﹣6（x﹣2）（x﹣9）令y'=0得x=2（∵x＞6，舍去）或x=9显然，当x∈（6，9）时，y'＞0当x∈（9，+∞）时，y'＜0∴函数y=﹣2x3+33x2﹣108x﹣108在（6，9）上是关于x的增函数；在（9，+∞）上是关于x的减函数．∴当x=9时，y取最大值，且y max=135．∴售价为9元时，年利润最大，最大年利润为135万元．点评：本小题主要考查根据实际问题建立数学模型，以及运用函数、导数的知识解决实际问题的能力．属于基础题．20．（12分）（2014•天津模拟）已知函数f（x）=x3﹣3ax2+b（x∈R），其中a≠0，b∈R．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）设a∈[，]，函数f（x）在区间[1，2]上的最大值为M，最小值为m，求M﹣m的取值范围．考点：利用导数研究函数的单调性；利用导数求闭区间上函数的最值．专题：导数的综合应用．分析：（Ⅰ）对于含参数的函数f（x）的单调区间的求法，需要进行分类讨论，然后利用导数求出函数的单调性；（Ⅱ）求出f（x）在[1，2a]内是减函数，在[2a，2]内是增函数，设 g（a）=4a3﹣12a+8，求出g（a）在[]内是减函数，问题得以解决．解答：解：（Ⅰ）f'（x）=3x2﹣6ax=3x（x﹣2a），令f'（x）=0，则x1=0，x2=2a，（1）当a＞0时，0＜2a，当x变化时，f'（x），f（x）的变化情况如下表：x （﹣∞，0）0 （0，2a）2a （2a，+∞）f'（x）+ 0 ﹣0 +f（x）↗极大值↘极小值↗∴函数f（x）在区间（﹣∞，0）和（2a，+∞）内是增函数，在区间（0，2a）内是减函数．（2）当a＜0时，2a＜0，当x变化时，f'（x），f（x）的变化情况如下表：x （﹣∞，2a） 2a （2a，0）0 （0，+∞）f'（x）+ 0 ﹣0 +f（x）↗极大值↘极小值↗∴函数f（x）在区间（﹣∞，2a）和（0，+∞）内是增函数，在区间（2a，0）内是减函数．（Ⅱ）由及（Ⅰ），f（x）在[1，2a]内是减函数，在[2a，2]内是增函数，又f（2）﹣f（1）=（8﹣12a+b）﹣（1﹣3a+b）=7﹣9a＞0，∴M=f（2），m=f（2a）=8a3﹣12a3+b=b﹣4a3，∴M﹣m=（8﹣12a+b）﹣（b﹣4a3）=4a3﹣12a+8，设 g（a）=4a3﹣12a+8，∴g'（a）=12a2﹣12=12（a+1）（a﹣1）＜0（a∈[]），∴g（a）在[]内是减函数，故 g（a）max=g（）=2+=，g（a）min=g（）=﹣1+4×=．∴≤M﹣m≤．点评：本题考查利用导数研究函数的极值和单调性，涉及构造函数的方法，属中档题．21．（12分）（2015•大观区校级四模）已知函数f（x）=ax+xlnx（a∈R）（1）若函数f（x）在区间[e，+∞）上为增函数，求a的取值范围；（2）当a=1且k∈z时，不等式k（x﹣1）＜f（x）在x∈（1，+∞）上恒成立，求k的最大值．考点：利用导数研究函数的单调性；利用导数求闭区间上函数的最值．专题：综合题；导数的概念及应用．分析：（1）易求f′（x）=a+1+lnx，依题意知，当x≥e时，a+1+lnx≥0恒成立，即x≥e 时，a≥（﹣1﹣lnx）max，从而可得a的取值范围；（2）依题意，对任意x＞1恒成立，令则，再令h（x）=x﹣lnx﹣2（x＞1），易知h（x）在（1，+∞）上单增，从而可求得g（x）min=x0∈（3，4），而k∈z，从而可得k的最大值．解答：解：（1）∵f（x）=ax+xlnx，∴f′（x）=a+1+lnx，又函数f（x）在区间[e，+∞）上为增函数，∴当x≥e时，a+1+lnx≥0恒成立，∴a≥（﹣1﹣lnx）max=﹣1﹣lne=﹣2，即a的取值范围为[﹣2，+∞）；（2）当x＞1时，x﹣1＞0，故不等式k（x﹣1）＜f（x）⇔k＜，即对任意x＞1恒成立．令则，令h（x）=x﹣lnx﹣2（x＞1），则在（1，+∞）上单增．∵h（3）=1﹣ln3＜0，h（4）=2﹣ln4＞0，∴存在x0∈（3，4）使h（x0）=0，即当1＜x＜x0时，h（x）＜0，即g′（x）＜0，当x＞x0时，h（x）＞0，即g′（x）＞0，∴g（x）在（1，x0）上单减，在（x0，+∞）上单增．令h（x0）=x0﹣lnx0﹣2=0，即lnx0=x0﹣2，=x0∈（3，4），∴k＜g（x）min=x0且k∈Z，即k max=3．点评：本题考查利用导数研究函数的单调性及利用导数求闭区间上函数的最值，着重考查等价转化思想与函数恒成立问题，属于难题．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.答时用2B 铅笔在答题卡上把所选题目的题号涂黑.选修4-1：几何证明选讲22．（10分）（2015•金昌校级模拟）如图，AB是⊙O的一条切线，切点为B，ADE、CFD都是⊙O 的割线，AC=AB，CE交⊙O于点G．（Ⅰ）证明：AC2=AD•AE；（Ⅱ）证明：FG∥AC．考点：与圆有关的比例线段；圆內接多边形的性质与判定．专题：选作题；立体几何．分析：（Ⅰ）利用切线长与割线长的关系及AB=AC进行证明．（Ⅱ）利用成比例的线段证明角相等、三角形相似，得到同位角角相等，从而两直线平行．解答：证明：（Ⅱ）∵AB是⊙O的一条切线，切点为B，ADE，CFD，CGE都是⊙O的割线，∴AB2=AD•AE，∵AB=AC，∴AD•AE=AC2．（Ⅱ）由（Ⅱ）有，∵∠EAC=∠DAC，∴△ADC∽△ACE，∴∠ADC=∠ACE，∵圆的内接四边形对角互补，∴∠ADC=∠EGF，∴∠EGF=∠ACE，∴FG∥AC．点评：本题考查圆的切线、割线长的关系，平面的基本性质．解决这类问题的常用方法是利用成比例的线段证明角相等、三角形相似等知识．选修4-4：坐标系与参数方程23．（2015•鹰潭一模）选修4﹣4：坐标系与参数方程．极坐标系与直角坐标系xoy有相同的长度单位，以原点为极点，以x轴正半轴为极轴，已知曲线C1的极坐标方程为ρ=4cosθ，曲线C2的参数方程为（t为参数，0≤α＜π），射线θ=φ，θ=φ+，θ=φ﹣与曲线C1交于（不包括极点O）三点A、B、C．（I）求证：|OB|+|OC|=|OA|；（Ⅱ）当φ=时，B，C两点在曲线C2上，求m与α的值．考点：简单曲线的极坐标方程；圆的参数方程．专题：直线与圆．分析：（Ⅰ）依题意，|OA|=4cosφ，|OB|=4cos（φ+），|OC|=4cos（φ﹣），利用三角恒等变换化简|OB|+|OC|为4cosφ，=|OA|，命题得证．（Ⅱ）当φ=时，B，C两点的极坐标分别为（2，），（2，﹣）．再把它们化为直角坐标，根据C2是经过点（m，0），倾斜角为α的直线，又经过点B，C的直线方程为y=﹣（x ﹣2），由此可得m及直线的斜率，从而求得α的值．解答：解：（Ⅰ）依题意，|OA|=4cosφ，|OB|=4cos（φ+），|OC|=4cos（φ﹣），…（2分）则|OB|+|OC|=4cos（φ+）+4cos（φ﹣）=2（cosφ﹣sinφ）+2（cosφ+sinφ）=4cosφ，=|OA|．…（5分）（Ⅱ）当φ=时，B，C两点的极坐标分别为（2，），（2，﹣）．化为直角坐标为B（1，），C（3，﹣）．…（7分）C2是经过点（m，0），倾斜角为α的直线，又经过点B，C的直线方程为y=﹣（x﹣2），故直线的斜率为﹣，…（9分）所以m=2，α=．…（10分）点评：本题主要考查把参数方程化为直角坐标方程，把点的极坐标化为直角坐标，直线的倾斜角和斜率，属于基础题．选修4-5：不等式选讲24．（2015•鹰潭一模）已知函数f（x）=|x+2|﹣2|x﹣1|（1）解不等式f（x）≥﹣2；（2）对任意x∈[a，+∞），都有f（x）≤x﹣a成立，求实数a的取值范围．考点：函数恒成立问题；绝对值不等式的解法．专题：函数的性质及应用；不等式的解法及应用；直线与圆．分析：（1）通过对x≤﹣2，﹣2＜x＜1与x≥1三类讨论，去掉绝对值符号，解相应的一次不等式，最后取其并集即可；（2）在坐标系中，作出的图象，对任意x∈[a，+∞），都有f（x）≤x﹣a成立，分﹣a≥2与﹣a＜2讨论，即可求得实数a的取值范围．解答：解：（1）f（x）=|x+2|﹣2|x﹣1|≥﹣2，当x≤﹣2时，x﹣4≥﹣2，即x≥2，∴x∈∅；当﹣2＜x＜1时，3x≥﹣2，即x≥﹣，∴﹣≤x≤1；当x≥1时，﹣x+4≥﹣2，即x≤6，∴1≤x≤6；综上，不等式f（x）≥﹣2的解集为：{x|﹣≤x≤6} …（5分）（2），函数f（x）的图象如图所示：令y=x﹣a，﹣a表示直线的纵截距，当直线过（1，3）点时，﹣a=2；∴当﹣a≥2，即a≤﹣2时成立；…（8分）当﹣a＜2，即a＞﹣2时，令﹣x+4=x﹣a，得x=2+，∴a≥2+，即a≥4时成立，综上a≤﹣2或a≥4．…（10分）点评：本题考查绝对值不等式的解法，考查分段函数的性质及应用，考查等价转化思想与作图分析能力，突出恒成立问题的考查，属于难题．。

宁夏银川一中2015届高三上学期第一次月考数学（理）试题一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知全集,{|2},{|1}U R A x x B x x ==≤-=≥，则集合（ ） A ． B ． C ． D ．2．下列函数中，在处的导数不等于零的是（ ） A. B. C. D. 3．已知，，则（ ）A ．B ．C ．D ．4．曲线在点P 处的切线的斜率为4，则P 点的坐标为（ ） A. B.或 C. D.或5．一元二次方程有一个正根和一个负根的充分不必要条件是（ ） A. B. C. D.6．已知函数是奇函数，当时，)10()(≠>=a a a x f x且 , 且，则的值为（ ） A. B. 3 C. 9 D.8. 已知奇函数在上单调递增，且，则不等式的解集是（ ） A. B. C. D. 9．函数的图象大致是（ ）10．若方程有实数根，则所有实数根的和可能是（ ）A. B. C. D.11．当时，，则的取值范围是（ ）A. (0，22)B. (22，1) C. (1，2) D.(2，2)12．当时，不等式恒成立，则实数的取值范围是（ ）A ．B ．C ．D ．第Ⅱ卷本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第24题为选考题，考生根据要求做答． 二、填空题：本大题共4小题，每小题5分，共20分. 13. 已知函数，当取最小值时， = . 14．计算由直线曲线所围成图形的面积 .15. 要制作一个容器为4，高为的无盖长方形容器，已知该容器的底面造价是每平方米20元，侧面造价是每平方米10元，则该容器的最低总造价是 （单位：元） 16. 给出下列四个命题： ①命题的否定是；②函数)10(11)(≠>+-=a a a a x f xx 且在上单调递减； ③设是上的任意函数， 则|| 是奇函数， +是偶函数； ④定义在上的函数对于任意的都有,则为周期函数；⑤命题p:，;命题q ：，。

宁夏银川一中2013届高三第一次模拟数学（理）试题2．已知i 为虚数单位，复数z=ii--221，则复数z 的虚部是A ．i 53-B ．53-C ．i 54D ．54 3．函数y=3x 与y=2)21(-x 图形的交点为（a ，b ），则a 所在区间是A ．（0，1） B ．（1，2 ）C ．（2，3 ） D ．（3，4） 4. 已知F 1、F 2是双曲线x 2a 2－y2b 2＝1(a>0， b>0)的两个焦点，以线段F 1F 2为边作正△MF 1F 2，若边MF 1的中点在双曲线上，则双曲线的离心率为A ．4＋2 3 B.3－1 C. 3＋12 D.3＋1 5. 阅读右边的程序框图，若输出S 的值为－14，则判断框内可填写A ．i<6? B ．i<8? C ．i<5? D.i<7? 6. 函数A ．在[0,),(,]22πππ上递增，在33[,),(,2]22ππππ上递减 B ．在3[0,),[,)22πππ上递增，在3(,],(,2]22ππππ上递减C ．在3(,],(,2]22ππππ上递增，在3[0,),[,)22πππ上递减D ．在33[,),(,2]22ππππ上递增，在[0,),(,]22πππ上递减7. 若某空间几何体的三视图如图所示，则该几何体的体积是A ． 13 B ．23C. 1D. 28. 已知点O 是边长为1的等边ABC △的中心，则()()OC OA OB OA +⋅+等于A ．19B ．19-C ．63-D ．16-9． 从6名同学中选4人分别到A 、B 、C 、D 四个城市游览，要求每个城市有一人游览，每人只游览一个城市，且这6人中甲、乙两人不去D 城市游览，则不同的选择方案共有A ．96种B ．144种 C ．240种D ．300种10．在直角坐标系xOy 中，已知△AOB 三边所在直线的方程分别为x=0,y=0,2x+3y=30，则△AOB 内部和边上整点（即横、纵坐标均为整数的点）的总数是 A ．95 B ．91 C ．88 D ．75 11. 已知抛物线23y x =-+上存在关于直线0x y +=对称的相异两点A、B，则AB 等于 A.3 B.4C.12. 设函数f(x)=x-1x,对任意0)()(),,1[<++∞∈x mf mx f x 恒成立，则实数m 的取值范围是A ．(-1 , 1) B. 0,≠∈m R m C. ∞（-，-1）D. ∞（-，-1）或（),1+∞ 二、填空题 13. 已知函数f (x )＝ax ＋1x ＋2在区间(－2，＋∞)上为增函数，则实数a 的取值范围是________________. 14. 已知向量25(cos ,sin ),(cos ,sin ),||.ab a b ααββ==-=则cos()αβ-的值为.15. 在三次独立重复试验中，事件A 在每次试验中发生的概率相同，若事件A 至少发生一次的概率为6364，则事件A 恰好发生一次的概率为 。

宁夏回族自治区银川一中2024-2025学年高三上学期第一次月考数学试卷一、单选题1．命题p ：x R ∀∈，2210x mx -+>的否定是 A ．x R ∀∈，2210x mx -+≤ B ．x R ∃∈，2210x mx -+< C ．x R ∃∈，2210x mx -+> D ．x R ∃∈，2210x mx -+≤2．已知函数21(1),()2(1).x x f x x x x -+<⎧=⎨-≥⎩，则()()1f f -的值为（ ）A ．2-B ．1-C ．3D ．03．“3a > ”是“函数2()(2)2f x a x x =-- 在(1,+)∞上单调递增”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件4．已知2081.5.12,,log 42a b c -⎛⎫⎝⎭=⎪==，则,,a b c 的大小关系为（ ）A ．c a b <<B ．c b a <<C ．b a c <<D ．b c a <<5．在同一个坐标系中，函数()log a f x x =，()x g x a -=，()ah x x =的图象可能是（ ）A ．B ．C ．D ．6．函数()f x ax x =的图象经过点(1,1)-，则关于x 的不等式29()(40)f x f x +-<解集为（ ） A ．(,1)(4,)-∞-+∞U B ．(1,4)- C ．(,4)(1,)∞∞--⋃+D ．(4,1)-7．中国宋代数学家秦九韶曾提出“三斜求积术”，即假设在平面内有一个边长分别为a ,b ,c 的三角形，其面积S 可由公式S =1=)2p a b c ++（，这个公式也被称为海伦-秦九韶公式，现有一个三角形的三边长满足14,6a b c +==，则此三角形面积的最大值为（ ）A ．6B ．C ．12D ．8．定义在R 上的偶函数()f x 满足()()1f x f x +=-，当[]0,1x ∈时，()21f x x =-+，设函数()()11132x g x x -⎛⎫=-<< ⎪⎝⎭，则函数()f x 与()g x 的图象所有交点的横坐标之和为A ．2B ．4C ．6D ．8二、多选题9．下列运算正确的是（ ）AB ．()326a a =C ．42log 32log 3=D ．2lg5lg2log 5÷=10．已知函数()y f x =是定义域为R 上的奇函数，满足(2)()f x f x +=-，下列说法正确的有（ ）A ．函数()y f x =的周期为4B ．(0)0f =C ．(2024)1f =D ．(1)(1)f x f x -=+11．已知函数()24,0,31,0,x x x x f x x -⎧-≥=⎨-<⎩其中()()()f a f b f c λ===，且a b c <<，则（ ）A ．()232f f -=-⎡⎤⎣⎦B ．函数()()()g x f x f λ=-有2个零点C ．314log ,45a b c ⎛⎫++∈+ ⎪⎝⎭D ．()34log 5,0abc ∈-三、填空题12．已知集合A ＝{}01x x ≤≤，B ＝{}13x a x -≤≤，若A ⋂B 中有且只有一个元素，则实数a 的值为．13．已知函数()()231m f x m m x +=+-是幂函数，且该函数是偶函数，则f的值是．14．已知函数()34x f x x =--在区间[1,2]上存在一个零点，用二分法求该零点的近似值，其参考数据如下：(1.6000)0.200f ≈，(1.5875)0.133f ≈，(1.5750)0.067f ≈，(1.5625)0.003f ≈，(1.5562)0.029f ≈-，(1.5500)0.060f ≈-，据此可得该零点的近似值为．（精确到0.01）四、解答题15．已知x ，y ，z 均为正数，且246x y z ==. (1)证明：111x y z+>；(2)若6log 4z =，求x ，y 的值，并比较2x ，3y ，4z 的大小. 16．已知函数()121(0),,R 4x f x m x x m=>∈+，当121x x =+时，()()1212f x f x +=. (1)求m 的值；(2)已知()120n n a f f f f n n n ⎫⎫⎫⎛⎛⎛=++++ ⎪ ⎪ ⎪⎝⎝⎝⎭⎭⎭L ，求n a 的解析式. 17．已知函数2ln(),0,()23,0,a x x f x x x x +-<⎧=⎨-++≥⎩且(e)3f -=． (1)求实数a 的值；(2)若函数()()=-g x f x k 在R 上恰有两个零点，求实数k 的取值范围．18．已知函数()e xf x =与函数()lng x x =，函数()()()11x g x g x ϕ=++-的定义域为D .(1)求()x ϕ的定义域和值域；(2)若存在x D ∈，使得(2)1()mf x f x ≥-成立，求m 的取值范围；(3)已知函数()y h x =的图象关于点(),P a b 中心对称的充要条件是函数()y h x a b =+-为奇函数.利用上述结论，求函数()1ey f x =+的对称中心.19．银行按规定每经过一定的时间结算存（贷）款的利息一次，结算后将利息并入本金，这种计算利息的方法叫做复利．现在某企业进行技术改造，有两种方案：甲方案：一次性向银行贷款10万元，技术改造后第一年可获得利润1万元，以后每年比上年增加30%的利润；乙方案：每年向银行贷款1万元，技术改造后第一年可获得利润1万元，以后每年比前一年多获利5000元．(1)设技术改造后，甲方案第n 年的利润．．为n a （万元），乙方案第n 年的利润．．为n b （万元），请写出n a 、n b 的表达式；(2)假设两种方案的贷款期限都是10年，到期一次性归还本息．若银行贷款利息均以年息10%的复利计算，试问该企业采用哪种方案获得的扣除本息后的净获利更多？（精确到0.1）（净获利=总利润-本息和）（参考数据101.1 2.594≈，101.313.79)≈。

银川一中 高三年级第一次月考数 学 试 题（理）第Ⅰ卷一、选择题（本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1．已知全集U=R ，集合A={x|-2≤x<0},B={x|2x-1<41},则C R （A ∩B ）= （ ）A ．（-∞，-2）∪[-1,+∞]B ． （-∞，-2]∪（-1,+∞）C ．（-∞,+∞）D ．（-2,+∞） 2．以下有关命题的说法错误的是（ ）A ．命题“若0232=+-x x 则x=1”的逆否命题为“若023,12≠+-≠x x x 则”B ．“1=x ”是“”0232=+-x x 的充分不必要条件C ．若q p ∧为假命题，则p 、q 均为假命题D ．对于命题01,:,01:22≥++∈∀⌝<++∈∃x x R x p x x R x p 均有则使得3．下列函数中,在),0(+∞上为减函数的是（ ）A ．xx f 3)(= B ．xx f 1)(-=C ．x x f =)(D ．x x f 21log )(=4．若函数)(x f y =的定义域是[0,2]，则函数1)2()(-=x x f x g 的定义域是 （ ）A ．[0,1]B ．[0,1]∪（1,4）C ．[0,1]D ．（0,1） 5．函数xx x f 2)1ln()(-+=的零点所在的大致区间是（ ）A ．（3，4）B ．（2，e ）C ．（1，2）D ．（0，1）6． 已知函数f （221)1xx xx +=-则f （3）= （ ） A ．8B ．9C ．10D ．11 7．函数[)⎪⎩⎪⎨⎧+∞∈-∞∈=,1,log )1,(,32x x x y x 的值域为（ ）A ．（0，3）B ．[0，3]C ．(]3,∞-D ．[)+∞,08．设a R ∈，函数()xxf x e a e -=+⋅的导函数是'()f x ，且'()f x 是奇函数。