化学反应器轴向扩散模型的应用分析

第一章绪论习题1.1 解题思路:（1）可直接由式（1.7）求得其反应的选择性（2）设进入反应器的原料量为100 ，并利用进入原料气比例，求出反应器的进料组成(甲醇、空气、水)，如下表：组分摩尔分率摩尔数根据式（1.3）和式（1.5）可得反应器出口甲醇、甲醛和二氧化碳的摩尔数、和。

并根据反应的化学计量式求出水、氧及氮的摩尔数，即可计算出反应器出口气体的组成。

习题答案:(1) 反应选择性(2) 反应器出口气体组成：第二章反应动力学基础习题2.1 解题思路:利用反应时间与组分的浓度变化数据，先作出的关系曲线，用镜面法求得反应时间下的切线，即为水解速率，切线的斜率α。

再由求得水解速率。

习题答案:水解速率习题2.3 解题思路利用式（2.10）及式（2.27）可求得问题的解。

注意题中所给比表面的单位应换算成。

利用下列各式即可求得反应速率常数值。

习题答案:(1)反应体积为基准(2)反应相界面积为基准(3)分压表示物系组成(4)摩尔浓度表示物系组成习题2.9 解题思路:是个平行反应，反应物A的消耗速率为两反应速率之和，即利用式（2.6）积分就可求出反应时间。

习题答案:反应时间习题2.11 解题思路:（1）恒容过程，将反应式简化为：用下式描述其反应速率方程：设为理想气体，首先求出反应物A的初始浓度，然后再计算反应物A的消耗速率亚硝酸乙酯的分解速率即是反应物A的消耗速率，利用化学计量式即可求得乙醇的生成速率。

（2）恒压过程，由于反应前后摩尔数有变化，是个变容过程，由式（2.49）可求得总摩尔数的变化。

这里反应物是纯A，故有：由式（2.52）可求得反应物A的瞬时浓度，进一步可求得反应物的消耗速率由化学计量关系求出乙醇的生成速率。

习题答案:（1）亚硝酸乙酯的分解速率乙醇的生成速率（2）乙醇的生成速率第三章釜式反应器习题3.1 解题思路:(1)首先要确定1级反应的速率方程式，然后利用式（3.8）即可求得反应时间。

(2)理解间歇反应器的反应时间取决于反应状态，即反应物初始浓度、反应温度和转化率，与反应器的体积大小无关习题答案:(1)反应时间t=169.6min.(2)因间歇反应器的反应时间与反应器的体积无关,故反应时间仍为169.6min.习题3.5 解题思路:（1）因为B过量，与速率常数k 合并成，故速率式变为对于恒容过程，反应物A和产物C的速率式可用式（2.6）的形式表示。

在自然界中，许多现象都可以用反应-扩散模型来描述。

反应-扩散模型是一种数学模型，它可以用来描述物质在空间和时间上的分布和变化。

反应-扩散模型广泛应用于各个领域，如化学、生物学、物理学、工程学等。

反应-扩散模型的基本原理是，物质在空间和时间上的分布和变化是由反应和扩散两个过程共同决定的。

反应是指物质之间的相互作用，导致物质的性质发生变化。

扩散是指物质从高浓度区域向低浓度区域移动的过程。

反应-扩散模型的数学形式一般为：其中，是物质的浓度，是时间，是扩散系数，是拉普拉斯算子，是反应函数。

反应-扩散模型可以用来描述许多自然现象，如：化学反应：化学反应是指物质之间的相互作用，导致物质的性质发生变化。

化学反应可以分为均相反应和非均相反应。

均相反应是指反应物和生成物都处于同一相，如气相反应、液相反应等。

非均相反应是指反应物和生成物处于不同相，如气-固反应、液-固反应等。

生物反应：生物反应是指生物体内的化学反应。

生物反应可以分为代谢反应和非代谢反应。

代谢反应是指生物体为了维持生命而进行的化学反应，如呼吸、光合作用等。

非代谢反应是指生物体为了适应环境而进行的化学反应，如排泄、分泌等。

物理反应：物理反应是指物质在物理性质上发生变化的反应。

物理反应可以分为相变反应和非相变反应。

相变反应是指物质从一种相变为另一种相，如熔化、凝固、汽化、液化等。

非相变反应是指物质在物理性质上发生变化，但没有发生相变，如吸附、解吸、溶解、结晶等。

反应-扩散模型是一种非常重要的数学模型，它可以用来描述许多自然现象。

反应-扩散模型在各个领域都有着广泛的应用，如化学、生物学、物理学、工程学等。

轴向扩散模型是一种常用于化学反应工程中的数学模型，用于描述流体在管道中的扩散和混合过程。

在MATLAB中，可以使用以下步骤来实现轴向扩散模型：1. 确定模型参数：轴向扩散模型需要输入一些参数，例如流体的密度、粘度、扩散系数等。

这些参数可以通过实验或其他方法得到。

2. 建立模型方程：轴向扩散模型通常使用Navier-Stokes方程和质量守恒方程来描述流体流动和扩散过程。

可以使用MATLAB中的向量和矩阵运算来建立模型方程。

3. 解模型方程：使用MATLAB中的数值求解器，例如fsolve函数，来求解模型方程。

可以使用不同的数值求解方法，例如中心差分法、有限差分法等。

4. 绘制结果：使用MATLAB中的图形绘制函数，例如plot函数，来绘制流体浓度随时间的变化曲线。

下面是一个简单的MATLAB代码示例，用于求解一个一维轴向扩散模型：定义参数rho = 1000; 流体密度mu = 1e-6; 流体粘度D = 1e-6; 流体扩散系数L = 1; 管道长度T = 1; 时间定义模型函数f = @(x, t) (rho * mu / D) * (1 - x(t+1) / L);求解模型方程x0 = linspace(0, L, T+1);x = fsolve(@(x) sum(x.^2), x0);绘制结果figure;plot(x(2:end), x(2:end));xlabel('时间');ylabel('流体浓度');在这个示例中，我们定义了一个简单的轴向扩散模型，使用MATLAB中的数值求解器求解模型方程，并使用plot函数绘制结果。

扩散模型的原理和应用教学设计1. 引言扩散模型是一种常用的数学模型，通过描述物质、信息或其他现象在空间中的传播和扩散过程，可以用于解决一系列实际问题。

本文将介绍扩散模型的原理和应用，并提出一套教学设计，帮助学生理解和应用扩散模型。

2. 扩散模型原理的概述扩散模型是基于扩散方程的数学模型，扩散方程是一个偏微分方程，描述了物质在时间和空间上的传播行为。

扩散模型的原理可以概括如下： - 扩散作用：物质在浓度梯度的驱动下从高浓度区向低浓度区传播。

- 扩散速率：扩散速率与浓度梯度成正比，与物质本身的性质和环境条件有关。

- 周期性模式：扩散过程在稳态时呈现周期性模式，即浓度分布在空间上呈现规则的波动。

3. 扩散模型的应用领域扩散模型在许多领域有着广泛的应用，以下列举几个典型的应用领域： - 生态学：研究生物种群、营养物质等在空间中的传播和分布。

- 环境科学：研究污染物、臭氧等在空气或水中的扩散和影响。

- 经济学：研究商品价格、信息传播等在市场中的扩散过程。

- 化学工程：研究物质在反应器内的扩散和传热过程。

- 计算机科学：研究网络中信息传播和扩散的规律。

4. 扩散模型应用教学设计为了帮助学生更好地理解和应用扩散模型，可以采用以下教学设计： ### 4.1理论知识讲解 - 向学生简洁明了地介绍扩散模型的原理和扩散方程的基本形式。

-通过具体的示例，说明扩散过程中的关键因素和规律。

- 引导学生思考扩散模型在不同领域中的应用，并探讨其意义和局限性。

4.2 实践应用探究•让学生分成小组，选择一个具体的领域或问题，设计扩散模型的数学表达式。

•鼓励学生使用数学软件或编程工具，模拟和求解问题，观察和分析结果。

•引导学生讨论模型的合理性和可靠性，以及模型在实际问题中的应用效果。

4.3 实例分析和展示•邀请专家或相关领域的从业者到课堂上，分享实际问题中扩散模型的应用案例。

•学生可以选择一个案例，进行深入研究和分析，并撰写报告或展示结果。

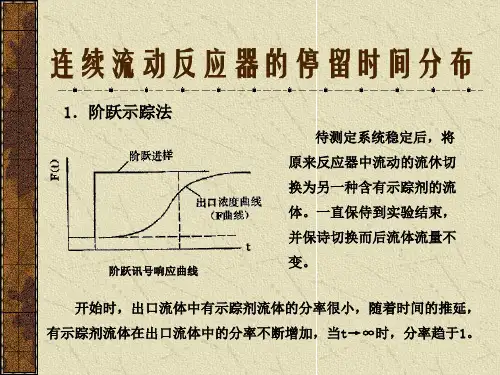
例 1。

1 在350℃等温恒容下纯丁二烯进行二聚反应，测得反应系统总压 p 与反应时间 t 的 关系如下:t/min 0612263860p/kPa66 。

762 。

358 。

953 。

550.446 。

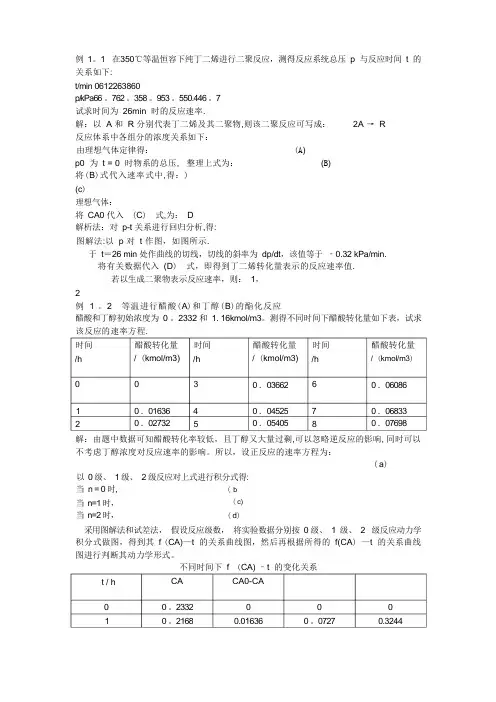
7试求时间为 26min 时的反应速率.解：以 A 和 R 分别代表丁二烯及其二聚物,则该二聚反应可写成： 2A → R 反应体系中各组分的浓度关系如下：由理想气体定律得： (A ) p0 为 t = 0 时物系的总压, 整理上式为： (B ) 将(B )式代入速率式中,得：) (c )理想气体：将 CA0 代入 (C ) 式,为： D解析法：对 p-t 关系进行回归分析,得: 图解法:以 p 对 t 作图，如图所示.于 t ＝26 min 处作曲线的切线，切线的斜率为 dp/dt ，该值等于 ‐0.32 kPa/min. 将有关数据代入 (D ) 式，即得到丁二烯转化量表示的反应速率值.若以生成二聚物表示反应速率，则： 1， 2例 1 。

2 等温进行醋酸(A )和丁醇(B )的酯化反应醋酸和丁醇初始浓度为 0 。

2332 和 1. 16kmol/m3。

测得不同时间下醋酸转化量如下表，试求 该反应的速率方程.解：由题中数据可知醋酸转化率较低，且丁醇又大量过剩,可以忽略逆反应的影响, 同时可以 不考虑丁醇浓度对反应速率的影响。

所以，设正反应的速率方程为：(a )以 0 级、 1 级、 2 级反应对上式进行积分式得:当 n = 0 时,当 n=1 时，当 n=2 时，(b (c)(d )采用图解法和试差法， 假设反应级数， 将实验数据分别按 0 级、 1 级、 2 级反应动力学 积分式做图，得到其 f (CA)—t 的关系曲线图，然后再根据所得的 f(CA ) —t 的关系曲线 图进行判断其动力学形式。

不同时间下 f (CA) –t 的变化关系CA0-CA0 0.01636CA0 。

2332 0 。

扩散模型的原理和应用视频1. 什么是扩散模型？扩散模型是一种数学方法，用于描述和预测物质的扩散过程。

它通过建立一组数学方程来描述扩散物质的传播行为，从而帮助我们理解和控制扩散过程。

扩散模型广泛应用于化学、生物学、环境科学、物流管理等领域。

2. 扩散模型的基本原理扩散模型的基本原理是基于扩散方程（Diffusion Equation）。

扩散方程是一个偏微分方程，描述了扩散物质在空间和时间上的变化。

扩散方程的一般形式如下：$$\\frac{\\partial u}{\\partial t} = D\ abla^2u$$其中，u表示扩散物质的浓度，t表示时间，D表示扩散系数，abla2u表示u的拉普拉斯算子。

扩散方程描述了扩散物质在空间和时间上的变化规律。

它的求解可以通过数值方法、解析方法或概率方法等来进行。

3. 扩散模型的应用领域扩散模型在多个领域都有广泛的应用，以下列举了几个常见的应用领域：3.1 化学反应中的扩散模型化学反应中的扩散模型用于描述反应物质在反应器中的传输过程。

通过建立扩散方程，可以预测反应物质的浓度分布、反应速率等参数，对化学反应的优化和控制起到重要作用。

3.2 生物学中的扩散模型生物学中的扩散模型用于研究细胞、器官和生物体内物质的传输过程。

通过建立扩散方程，可以分析细胞内物质的扩散速率、浓度分布等参数，对生物学研究具有重要意义。

3.3 环境科学中的扩散模型环境科学中的扩散模型用于分析和预测污染物在大气、水体和土壤中的传输和扩散过程。

通过建立扩散方程，可以评估污染物的扩散范围、浓度分布，并为环境污染的治理提供科学依据。

3.4 物流管理中的扩散模型物流管理中的扩散模型用于优化货物的运输和配送过程。

通过建立扩散方程，可以分析货物在仓库、运输车辆等场景中的传递和分布，从而优化物流路线、减少运输成本。

4. 如何进行扩散模型的建模？进行扩散模型的建模可以遵循以下几个步骤：1.定义问题：明确需要研究的问题，确定模型的范围和目标。

扩散模型的原理和应用1. 扩散模型的概述扩散模型是一种数学模型，用于描述物质、信息或疾病等在空间和时间上的扩散过程。

它基于一些假设和规则，通过数学方法推导出扩散的行为和特征。

扩散模型广泛应用于各个领域，包括物理学、化学、生物学、金融学等，用于解释和预测各种扩散现象。

2. 扩散模型的基本原理扩散模型的基本原理是通过描述扩散物质在空间和时间上的变化，并根据一定的规则和条件来推导出物质扩散的行为。

一般来说，扩散模型包括以下几个要素：•扩散方程：用于描述物质扩散的数学方程，通常是一个偏微分方程。

例如，常见的扩散方程包括热传导方程、扩散方程等。

•初始条件：描述物质扩散的起始状态，包括物质分布、浓度等信息。

•边界条件：描述物质扩散的边界情况，包括边界处的浓度、梯度等。

•扩散系数：描述物质扩散的速率和性质，通常与物质的性质、环境条件等相关。

3. 扩散模型的应用领域扩散模型在各个领域均有广泛的应用，以下是一些典型的应用领域：3.1 物理学领域在物理学中，扩散模型被用于研究热传导、电子扩散、光子扩散等现象。

通过建立适当的数学模型，可以预测温度、电子、光子等在物质中的扩散行为，从而进一步研究物质的性质和特性。

3.2 生物学领域在生物学中，扩散模型被用于研究细胞内物质的扩散、化学物质在生物体中的传播等现象。

通过建立适当的数学模型，可以分析物质在细胞内外的传输行为，为解释生物学过程提供理论依据。

3.3 化学领域在化学领域，扩散模型被用于研究化学物质的扩散和反应过程。

通过建立适当的数学模型，可以预测化学物质在不同环境中的扩散速率、反应速率等，从而指导实际化学实验和工业生产。

3.4 金融学领域在金融学中，扩散模型被用于研究金融市场中的信息传播和价格演化等现象。

通过建立适当的数学模型，可以模拟和预测金融资产价格的变化，为投资者决策提供参考和预测。

4. 扩散模型的局限性尽管扩散模型在各个领域有广泛的应用，但也存在一定的局限性。

扩散反应的动力学研究及其应用价值扩散反应，是指在物质分子间自由运动的过程中，分子进入其他物体中并与其发生反应的过程。

其研究已经有了相当深入的了解，并且对社会具有重要的应用价值。

本文将探讨扩散反应的动力学研究及其应用价值。

一、扩散反应的动力学研究扩散反应动力学研究是很多领域的基础工作，如材料科学、化学、生物学等领域均有其应用。

其中很多研究方法都依赖于扩散反应动力学的基本原理，这就要求对扩散反应的动力学进行深入的研究。

扩散反应动力学理论的基础是Fick定律，该定律描述的是扩散的速度。

根据Fick定律，扩散通常会发生在一个浓度梯度的存在下。

此外，扩散速率也与各种因素有关，如温度、压强和空气湿度等。

扩散反应动力学研究不仅依赖于理论模型，还需要结合实验技术进行实验验证。

动力学研究通常需要仔细控制条件，包括反应物浓度、温度等因素。

此外，还需对实验中的扩散动力学过程进行实时监测和分析。

二、扩散反应的应用价值扩散反应的应用价值十分广泛，下面列举一些关键领域：1. 化学扩散反应在化学领域中被广泛应用。

许多化学反应需要扩散动力学下的基本原理，如催化剂和反应动力学的表征等。

2. 材料科学在材料科学方面，扩散反应的动力学研究可以用于引导材料结构和性能，以提高材料强度、硬度和其他机械性质。

3. 生物学扩散反应的研究对生物学领域具有重要意义，特别是在药物输送、外科手术设计、组织工程和食品加工等方面。

4. 环境保护扩散反应在环境保护方面也需要进行研究。

例如，在煤炭锅炉燃烧过程中，需要了解氧气扩散的速度以便维持合理的燃烧。

5. 能源领域在能源领域，向氢气储存的应用依赖于扩散动力学的理论，也就是氢气与材料之间的扩散反应。

6. 质量控制和品质保证扩散可以帮助评估质量控制和品质保证方面的问题。

质量控制主要涉及工业制品的生产过程中的工艺控制、机械过程和相关关键性能的确定。

7. 生物医疗扩散反应在医学方面的应用可追溯到早期诊断和治疗疾病的历史。

反应扩散模型在化学反应中的应用研究化学反应是学习化学的重要内容，其中反应速率是一个重要的参数。

反应速率与反应物浓度之间存在着一定的关系，即浓度越高，反应速率越快。

但是在实际应用中，反应速率不仅与浓度有关，还与温度、催化剂等因素有关。

为了更好地研究这些因素对反应速率的影响，科学家们提出了反应扩散模型，该模型在化学反应研究中具有广泛的应用。

一、什么是反应扩散模型反应扩散模型是一种用来描述反应物在微观尺度下扩散的数学模型。

该模型基于分子动力学理论，考虑了反应物浓度、结构和相互作用等因素，可以用来预测反应速率和反应机理。

在化学反应研究中，反应扩散模型主要应用于液体、气体和固体表面上的化学反应。

例如，在催化剂作用下，气态反应物在固体催化剂表面上发生反应，此时反应扩散模型可以用来预测反应速率和反应机理。

二、反应扩散模型在化学反应中的应用1、反应速率的预测在化学反应中，反应速率是一个重要的参数。

反应速率与反应物浓度之间存在着一定的关系，即浓度越高，反应速率越快。

但是在实际应用中，反应速率不仅与浓度有关，还与温度、催化剂等因素有关。

为了更好地研究这些因素对反应速率的影响，科学家们提出了反应扩散模型。

反应扩散模型可以用来预测反应速率和反应机理。

在反应速率预测方面，反应扩散模型基于分子动力学理论，考虑了反应物浓度、结构和相互作用等因素。

通过计算这些因素的影响，反应扩散模型可以帮助科学家们预测反应速率。

例如，在研究催化反应时，反应扩散模型可以帮助科学家们预测催化剂表面上的反应物浓度，从而确定反应速率。

此外，反应扩散模型还可以用来分析反应物分子在催化剂表面上的反应路径，从而预测反应机理。

2、反应动力学的研究反应扩散模型不仅可以用来预测反应速率和反应机理，还可以用来研究反应动力学。

反应动力学是研究反应速率和反应机理的学科，其研究对象是活性物质在反应物中的相对浓度和反应速率的关系。

在化学反应中，反应动力学研究的是反应物浓度随时间的变化规律。

轴向扩散模型的唯一模型参数轴向扩散模型是一种用于描述物质在空间中传播的模型。

它基于一个简单而有力的假设：物质从高浓度区域向低浓度区域扩散，直到浓度均匀分布。

这个假设可以应用于各种不同的领域，包括化学、物理、生物等。

在化学领域，轴向扩散模型被广泛用于描述溶质在溶液中的扩散过程。

当溶质在溶液中存在浓度梯度时，它会向浓度较低的区域扩散，直到达到均匀分布。

这个过程可以用轴向扩散模型来解释，其中唯一的模型参数就是扩散系数。

扩散系数反映了溶质在溶液中扩散的速度和效率，它与溶质的性质、溶液的温度等因素有关。

在物理领域，轴向扩散模型可以用于描述热量在材料中的传导过程。

当材料的一部分受热时，热量会向周围区域扩散，直到整个材料达到热平衡。

轴向扩散模型可以用来计算热量在材料中的传导速率，其中扩散系数表示材料的导热性能。

不同材料的导热性能不同，因此扩散系数也不同。

在生物领域，轴向扩散模型被应用于描述细胞内物质的运输过程。

细胞内存在着各种物质，如离子、蛋白质等，它们需要在细胞内迅速传递到目标位置。

轴向扩散模型可以用来模拟这个过程，其中扩散系数表示物质在细胞内传输的速率和效率。

细胞内的扩散系数受到细胞结构、分子大小等因素的影响。

除了以上几个领域，轴向扩散模型还可以应用于其他许多领域。

例如，在环境科学中，它可以用来描述污染物在土壤或水体中的传播过程；在金融领域，它可以用来描述资金在市场中的流动过程。

无论在哪个领域，轴向扩散模型都以其简洁而有效的描述方式得到了广泛应用。

然而，轴向扩散模型也有其局限性。

首先，它仅适用于均匀介质中的扩散过程，不能描述非均匀介质中的复杂扩散行为。

其次，轴向扩散模型忽略了其他因素对扩散过程的影响，如流体流动、化学反应等。

因此，在实际应用中，需要结合其他模型和方法来更准确地描述扩散过程。

轴向扩散模型是一种简单而有效的描述物质扩散过程的模型。

通过控制唯一的模型参数-扩散系数，我们可以定量地描述物质在空间中的传播行为。

化学反应器动力学模型的建立与应用化学反应器是化工生产中的重要设备之一，是进行化学反应的装置。

为了控制反应过程，提高反应效率和产品质量，需要对反应过程进行深入的分析和研究。

而化学反应器动力学模型的建立和应用正是实现这个目标的重要手段。

一、化学反应器动力学模型的意义化学反应器动力学模型是通过分析反应物在反应中的消耗变化以及产物的生成规律，建立反应过程数学模型，并利用数学方法来解决反应过程中的一系列问题。

该模型的建立和应用可以使我们更好地掌握反应器的反应过程，预测反应物的消耗和产物的生成情况，为工艺设计和生产控制提供准确的理论依据。

二、化学反应器动力学模型的建立方法化学反应器动力学模型的建立基本分为以下几个步骤：1. 定义反应物、产物和中间物的化学式以及反应的速率方程。

2. 确定反应机理和反应条件。

3. 利用微观或宏观角度分析反应过程，并建立反应数学模型。

4. 确定模型参数，例如反应速率常数、扩散系数、物质传递系数等。

5. 利用计算方法或实验数据验证模型的合理性。

三、化学反应器动力学模型的应用化学反应器动力学模型的应用包括以下几个方面：1. 预测反应物的消耗量和产物的生成量，为反应器的工艺设计提供参考。

2. 优化反应条件，提高反应效率和产品质量。

3. 模拟反应过程，提前预知反应器的性能并进行调整，减少产品损失和资源浪费。

4. 为反应器的控制和监测提供理论依据，优化反应器的操作。

四、化学反应器动力学模型的实例以简单的酯化反应为例，说明化学反应器动力学模型的建立和应用。

在酯化反应中，反应物A和B会共同反应生成产物C和D，反应速率方程可以写作：r=kCACB其中，k为反应速率常数，CA和CB分别为反应物A和B的浓度。

由于该反应是二级反应，因此可以假定反应是由一个中间物E经过一个快速的反应生成物质C和D的。

因此，反应的细节可以写为：A+E→FF+B→C+D其中E和F是中间物，由于反应速率快，可以忽略它们在反应过程中的变化。