分组密码体制-精
- 格式:ppt
- 大小:9.34 MB
- 文档页数:197

分组密码体制简介分组密码体制也具有简捷、快速的特点,并且容易标准化,使其成为软硬件加密的主流算法。
目前主流的分组密码有:DES、IDEA…… .1.分组密码的特点与序列密码不同,分组密码是将明文序列划分成等长的分组(Block),对每一组用同一加密算法和同一密钥进行加密。
分组密码有其自身的优点,首先分组密码容易被标准化,因为在今天的数据网络通信中,信息通常是被成块的处理和传输的。
其次,使用分组赌东道密码容易实现同步,因为一个密码组的传输错误不会影响到其它的分组,丢失一个密文组不会对随后组的解密产生影响。
这就是说,传输错误不会扩散。
而这些方面恰恰是序列密码的最大缺点。
分组密码与序列密码相比的一个缺点就是算法庞大一些,需要更多的计算资源。
分组密码的另一大缺点是其安全性很难被证明。
尽管“可证明安全性”的研究发展很快,但目前的分组密码大多是“看来安全的”,还没有一个分组密码被证明是真正安全的,至多证明了局部安全性。
这其中的原因是:因商业化而要求分组密码算法的细节全部暴露,因此对分组密码的攻击类型很多,安全性概念也就很多,有人为了统一这些安全性概念,甚至引入了伪随机性和超伪随机性,它们是用概率图灵机来描述的,在实际设计和分析中很难应用。
2.分组密码的设计准则一、安全性准则对以下的安全性的描述总是基于以下的假设:加密体制(包括算法的细节)是公开的;安全性完全依赖于密钥;信道是不安全的,即攻击者可以任意的截取密文;攻击者有时也可以截取一些“废弃”的明文。
(1)分组长度和密钥长度:当明文分组长度为n比特时,至多需要2n个明文-密文对就可以彻底破解密钥。
同理当密钥长度为n比特时,对一个截获的密文,至多需要试验2n个密钥就可以破解了密文。
因此从安全性角度来考虑,明文分组长度的密钥长度因尽可能的大。
(2)混淆性:所设计的密码应使得明文、密文、密钥之间的依赖关系相当复杂,以至于这种依赖关系对密码分析者来说是无法利用的。





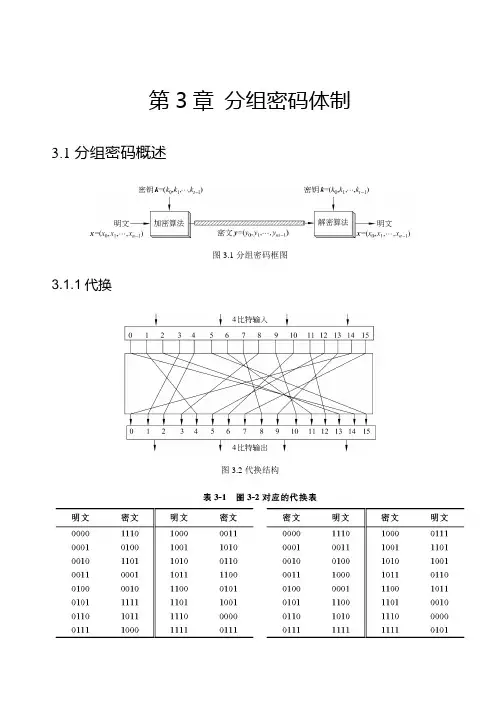
第3章分组密码体制3.1分组密码概述图3.1分组密码框图3.1.1代换图3.2代换结构2现代密码学(第2版)3.1.2扩散和混淆3.1.3 Feistel密码结构1. Feistel加密结构图3.3 Feistel网络2. Feistel解密结构现代密码学(第2版) 3图3.4 Feistel加解密过程4现代密码学(第2版)3.2数据加密标准3.2.1DES描述图3.5 DES加密算法框图1. 初始置换现代密码学(第2版) 52. 轮结构图3.6 DES加密算法的轮结构图3.7函数F(R,K)的计算过程6现代密码学(第2版)3. 密钥的产生现代密码学(第2版)7图3.8二重DES8现代密码学(第2版)3.2.3两个密钥的三重DES图3.9两个密钥的三重DES 3.2.4 3个密钥的三重DES3.3差分密码分析与线性密码分析3.3.1差分密码分析3.3.2线性密码分析3.4分组密码的运行模式现代密码学(第2版)93.4.1电码本(ECB)模式图3.10 ECB模式示意图10现代密码学(第2版)3.4.2密码分组链接(CBC)模式图3.11 CBC模式示意图3.4.3密码反馈(CFB)模式图3.12 CFB模式示意图3.4.4输出反馈(OFB)模式图3.13 OFB模式示意图3.5 IDEA3.5.1设计原理1. 密码强度图3.14 MA 结构2. 实现3.5.2加密过程图3.15 IDEA的加密框图1. 轮结构图3.16 IDEA第1轮的轮结构图3.17 IDEA的输出变换2. 子密钥的产生3. 解密过程图3.18 IDEA加密和解密框图3.6 AES 算法——Rijndael3.6.1 Rijndael的数学基础和设计思想1. 有限域GF(28)2. 系数在GF(28)上的多项式3. 设计思想3.6.2算法说明1. 状态、种子密钥和轮数2. 轮函数图3.19字节代换示意图图3.20行移位示意图图3.21列混合运算示意图图3.22密钥加运算示意图3. 密钥编排图3.23 Nb=6且Nk=4时的密钥扩展与轮密钥选取4. 加密算法5. 加解密的相近程度及解密算法习题。

分组密码模式分组密码模式分组密码与流密码分组密码:每次只能处理特定长度的⼀块数据的⼀类算法,“⼀块”就称为分组(block )。
⼀个分组的⽐特数就称为分组长度(block length)。
流密码: 对数据流进⾏连续的处理的⼀类密码。
只有⼀次性密码本属于流密码,⽽DES 、三重DES 、AES 等⼤多数对称密码算法都属千分组密码。
模式分组密码算法只能加密固定产固定的分组,若加密的铭⽂的长度超过分组密码的长度,需要对分组密码算法进⾏迭代,以便将所有的密码全部加密。
明⽂分组和密⽂分组主动攻击者Mallory窃听者Eve 只能被动地进⾏窃听,⽽主动攻击者则可以主动介⼊发送者和接收者之间的通信过程,进⾏阻碍通信或者是篡改密⽂等活动。
这样的攻击者⼀般称为Mallory 。
ECB模式使⽤ECB 模式加密时,相同的明⽂分组会被转换为相同的密⽂分组,也就是说,我们可以将其理解为是⼀个巨⼤的“明⽂分组⼀密⽂分组”的对应表,因此ECB 模式也称为电⼦密码本模式。
当最后⼀个明⽂分组的内容⼩于分组长度时,需要⽤⼀些特定的数据进⾏填充( padding )。
CBC 模式在CBC 模式中,⾸先将明⽂分组与前⼀个密⽂分组进⾏XOR 运算,然后再进⾏加密。
ECB 和 CBC 的区别初始化向量当加密第⼀个明⽂分组时,由于不存在“前⼀个密⽂分组”,因此需要事先准备⼀个长度为⼀个分组的⽐特序列来代替“前⼀个密⽂分组”,这个⽐特序列称为初始化向量(Initialization Vector) ,通常缩写为IV 。
⼀般来说,每次加密时都会随机产⽣⼀个不同的⽐特序列来作为初始化向量。
CBC模式的特点明⽂分组在加密之前⼀定会与“前⼀个密⽂分组”进⾏XOR 运算,因此即便明⽂分组 1和 2 的值是相等的,密⽂分组1 和 2 的值也不⼀定是相等的。
这样⼀来,ECB 模式的缺陷在CBC模式中就不存在了。
在CBC 模式中,我们⽆法单独对⼀个中间的明⽂分组进⾏加密。

分组密码分组密码概述所谓分组密码,简单地说就是对明⽂进⾏分组,每组的长度都相同,然后对每组明⽂使⽤密钥进⾏加密得密⽂,解密即对每组明⽂使⽤密钥进⾏解密得到明⽂。
通常情况是明⽂、密⽂等长。
(好处是处理速度快,节约了存储,避免了浪费带宽.)1. 定义分组密码包含5个部分{M,C,K,E,D},M=F(2,n)明⽂空间K=F(2,k)密钥空间C=F(2,n)密⽂空间E加密变换;D解密变换明⽂m1m2……mn通过密钥k加密算法得到密⽂c1c2……cn分组密码是⼀种映射:E:M*K->CD:C*K->M注:分组密码实际上是{0,1,2,……,2^n-1}到其⾃⾝的⼀⼀映射,密钥k不同映射不同。
2. 基本要求分组长度⾜够长(防⽌明⽂穷举攻击)密钥长度⾜够长(防⽌密钥穷举攻击)加解密算法要⾜够复杂(能抗击各种已知攻击)3. 分组密码的原则为有效抵抗对密码体质的通知分析,⾹农提出了两个原则:扩展原则和混乱原则。
扩散:指每1bit明⽂的变化尽可能多地影响密⽂序列的bit,以隐蔽明⽂的统计特性,防⽌对密钥进⾏逐段攻击破译;混乱:指加密变换过程中明⽂、密钥以及密⽂之间的关系尽可能的复杂,以防⽌破译者采⽤统计分析⽅法进⾏攻击。
4. 分组密码的结构(SP⽹络)需求分析:⼀个分组密码既要难于分析(复杂),⼜要易于实现(简单),迭代密码可克服这⼀对⽭盾。
其加密变换⼀般采取如下结构:由⼀个简单的函数F(易于实现)迭代若⼲次⽽形成。
其中Yi-1是第i轮迭代的输⼊,Yi是第i轮的输出,Zi由密钥k导出,这类密码即迭代密码。
如DES是16轮迭代密码,多次迭代可实现必要的混乱与扩散。
F函数采⽤代换置换结构,置换由P盒实现,起扩散作⽤,代换可提供混淆作⽤,其中代换被精⼼设计且起关键作⽤,⼈们常称其为“⿊盒⼦”。
SP结构具有雪崩效应,雪崩效应指输⼊(明⽂或密钥)即使只有很⼩的变化,也会导致输出(密⽂)产⽣巨⼤的变化。

