一阶动态响应电路分析
- 格式:docx
- 大小:192.08 KB
- 文档页数:6

RC一阶电路的响应测试实验报告实验报告:RC一阶电路的响应测试一、实验目的:1.掌握RC一阶电路的响应特性;2.了解RC一阶电路的时间常数对电路响应的影响;3.学会使用示波器观察电路的动态响应。
二、实验原理:由于充电或放电需要一定的时间,电路的响应是有延迟的。
根据电容充电时间常数τ的不同,可以将RC电路分为快速响应和慢速响应两种情况。
电容C的充电或放电方程为:i(t) = C * dV(t) / dt根据Ohm's Law,电路中的电流和电压之间的关系为:V(t) = VR(t) + VC(t) = i(t) * R + V0 * exp(-t/τ)其中,VR(t)是电阻R上的电压,VC(t)是电容C上的电压,V0是电路初始电压,τ=C*R是电路的时间常数。
当输入信号为直流电压时,电路将会处于稳态,电容将保持充电或放电状态,直到与电源电压相等。
当输入信号为瞬态电压时,电路将会发生响应,电容充放电的过程导致电压变化。
三、实验器材和仪器:1.RC电路板;2.直流电源;3.示波器;4.电阻和电容。
四、实验步骤:1.将示波器的地线和信号触发线接地。
2.按照实际电路中的元件数值,在RC电路板上连接电阻和电容。
3.将示波器的一个探头连接到电阻两端,另一个探头连接到电容的一端。
4.打开直流电源,设定合适的电压大小,使电路处于稳定状态。
5.调整示波器的触发模式和触发电平,保证波形稳定可观察。
6.增加或减小直流电压,观察电路响应,并记录波形。
7.改变电阻或电容的数值,重复步骤6,观察并记录不同响应特性。
8.关闭直流电源和示波器,取下电路连接。
五、实验数据及结果:实验中,我们首先建立了一个由1000Ω电阻和0.1μF电容串联组成的RC电路。
然后,我们分别给电路输入不同幅值和时间常数的矩形波信号,观察电路的响应。
1.输入直流电压的稳态响应:当输入直流电压时,电路处于稳态,电容已经充电到与电源电压相等的电压值。


一阶电路动态响应实验报告一、实验报告概述一阶电路动态响应这个实验啊,可有意思啦。
这就像是探索电路世界里的一个小秘密一样。
咱这个实验呢,就是要看看电路在不同的初始条件下,它是怎么随着时间变化而做出反应的。
这就好比是观察一个小生物,看它在不同环境里是怎么生存的。
二、实验目标1. 我们要搞清楚一阶电路动态响应的特点。
就像是认识一个新朋友,要知道他的脾气秉性一样。
2. 学会用实验仪器来测量相关的数据。
这就像是厨师要学会用锅碗瓢盆做出美味佳肴一样。
3. 能够根据实验数据画出准确的响应曲线。
这曲线就像是这个电路的一张画像,能让我们一眼看出它的变化情况。
三、实验重点和难点1. 重点准确连接电路。
这就像是搭积木,每一块都要放对位置,不然整个电路就没法正常工作啦。
正确读取实验仪器的数据。
这数据可不能读错呀,读错了就像认错了路,会把我们带偏的。
2. 难点理解动态响应的概念。
这个概念有点抽象呢,就像雾里看花,要费点功夫才能看清楚。
对实验中出现的误差进行分析。
误差就像调皮的小捣蛋鬼,要找出它是从哪里冒出来的可不容易。
四、实验方法1. 我们采用的是实验测量法。
就像探险家拿着地图和工具去探索未知的地方一样,我们拿着仪器去测量电路的各种参数。
2. 还有对比法。
把不同条件下的实验结果进行对比,就像比较两个苹果,看哪个更甜一样。
五、实验过程1. 电路连接首先把电源、电阻、电容这些元件都拿出来。
就像准备食材一样,要把做菜的材料都准备好。
然后按照电路图小心翼翼地连接起来。
这时候要特别小心,就像走钢丝一样,一步都不能错。
我会跟同学们说:“同学们啊,这电路连接就像搭乐高积木,每个零件都有它的位置,可不能乱放哦。
”要是有同学接错了,我会笑着说:“哎呀,这个小零件跑错地方啦,咱们把它送回正确的家吧。
”2. 数据测量打开电源之后呢,我们就用仪器开始测量电压和电流啦。
这时候要眼睛紧紧盯着仪器的显示屏,就像小侦探在寻找线索一样。
我会提醒同学们:“大家的眼睛要像老鹰一样锐利哦,别错过任何一个数据。


一阶动态电路响应的研究实验目的:1.学习函数信号发生器和示波器的使用方法。
2.研究一阶动态电路的方波响应。
实验仪器设备清单:1.示波器 1台2.函数信号发生器 1台3.数字万用表 1块4. 1kΩ电阻X1 ;10kΩ电阻 X1 ;100nf电容X1 ;面包板;导线若干。
实验原理:1.电容和电感的电压与电流的约束关系是通过导数和积分来表达的。
积分电路和微分电路时RC一阶电路中典型的电路。
一个简单的RC串联电路,在方波序列脉冲的重复激励下,由R两端的电压作为输出电压,则此时该电路为微分电路,其输出信号电压与输入电压信号成正比。
若在该电路中,由C两端的电压作为响应输出,则该电路为积分电路。
2.电路中在没有外加激励时,仅有t=0时刻的非零初始状态引起的响应成为零输入响应,其取决于初始状态和电路特性,这种响应随时间按指数规律衰减。
在零初始状态时仅有在t=0时刻施加于电路的激励所引起的响应成为零状态响应,其取决于外加激励和电路特性,这种响应是由零开始随时间按指数规律增长的。
线性动态电路的全响应为零输入响应和零状态响应之和。
实验电路图:实验内容:1.操作步骤、:(1).调节信号源,使信号源输出频率为1KHz,峰峰值为1.2VPP的方波信号。
(2).将示波器通道CH1与信号源的红色输出端相接,黑色端也相接,调示波器显示屏控制单位,使波形清晰,亮度适宜,位置居中。
(3).调CH1垂直控制单元,使其灵敏度为0.2V,即在示波器上显示出的方波的幅值在屏幕垂直方向上占6格。
(4).调CH2水平控制单元,使其水平扫描速率为0.2ms,表示屏幕水平方向每格为0.2ms。
(5).按照实验原理的电路图接线,将1K电阻和10nf电容串联,将信号源输出线的红色夹子,示波器CH1的红色夹子连电阻的一端,电容的另一端与信号源,示波器的黑色夹子连在一起,接着将CH2的输入探极红色夹子接在电容的非接地端,黑色夹子接在电容的接地端。
(6).打开信号源开关,示波器CH1,CH2通道开关,观察示波器并记录其波形。

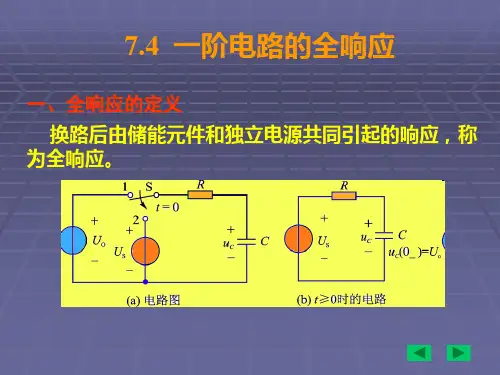
一阶动态电路的全响应好嘞,今天我们来聊聊一阶动态电路的全响应。
说到这,大家可能会觉得有点复杂,不过别担心,我会用轻松的方式给你讲明白的。
想象一下,你在家里喝茶,偶尔抬头看看窗外,看到那微风吹过的树叶,忽然想起了电路。
听起来是不是有点奇怪?但电路其实就像生活中的很多事情,有时候一阵风吹来,你的反应会慢半拍,这就跟一阶动态电路一样。
一阶动态电路是什么呢?简单说,就是那种反应不那么迅速的电路。
就像你在思考一件事情时,脑子里可能会卡壳。
电流流动的速度不是瞬间就能达到,而是有个逐渐适应的过程。
就像你早上醒来,不是一下子就能进入状态,得喝杯咖啡,等一等才行。
电路也是,输入信号来了,输出信号得等一等,慢慢才能反应过来。
这种反应过程就叫全响应。
我们来想象一下,一个简单的电路。
假设有个电阻和电容,电压信号突然加上去。
这时候,电容就像个小水库,水库里的水不能一下子装满,得一点点来,慢慢充水。
这个过程就是电容充电的过程,电流逐渐增大,电压也渐渐上升。
你可以把它想象成一个人慢慢适应新环境,刚到一个派对,开始有点紧张,慢慢就能放开来,跟大家聊得热火朝天。
然后啊,电路的全响应不仅仅是充电,放电也是一回事。
电容充好电了,假如这个电源突然断了,电容里的电就像气球里的空气,开始慢慢漏出去。
这时候,电压又会渐渐下降,直到完全放空。
这种变化其实在生活中也很常见,比如你跟朋友聊天,聊得正嗨,结果突然有人打断了,你可能一时没反应过来,脑子里还在回味刚才的话题。
说到这里,可能会有人问,全响应有什么用呢?嘿,这可大有用处了。
你想啊,很多电子设备都需要控制信号的变化速率。
比如说在音响里,如果信号变化太快,可能会造成声音失真,就像是你跟朋友聊天,他话说得太快,你根本跟不上。
反过来,如果反应太慢,又会造成滞后,影响使用体验。
我们再说说这个电路的时间常数。
这个时间常数就像你给电路加个标签,告诉它“嘿,反应时间差不多是多久”。
时间常数越大,反应越慢;越小,反应越快。

一、实验目的1. 了解动态电路的基本原理和特性;2. 掌握一阶动态电路的响应规律;3. 熟练使用示波器、信号发生器等实验仪器;4. 提高实验操作能力和数据处理能力。
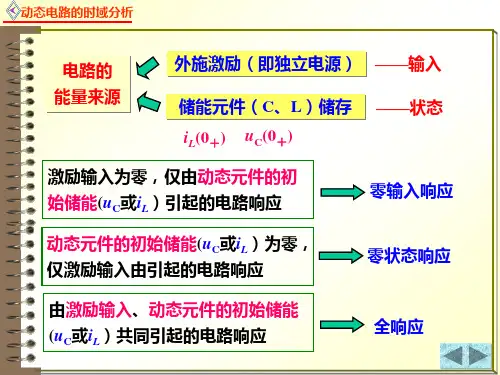
二、实验原理动态电路是指电路中含有电容或电感元件的电路。
在动态电路中,电容和电感元件的电压与电流之间的关系可以用导数和积分来描述。
一阶动态电路的响应规律主要由时间常数决定,时间常数τ = RC或τ = L/R,其中R为电阻,C为电容,L为电感。
一阶动态电路的响应分为三种:零输入响应、零状态响应和完全响应。
零输入响应是指在没有外加激励的情况下,仅由电路的初始状态引起的响应;零状态响应是指在外加激励作用下,电路的初始状态为零时的响应;完全响应是零输入响应和零状态响应的和。
三、实验仪器与设备1. 示波器 1台;2. 信号发生器 1台;3. 函数信号发生器 1台;4. 电阻(R1K、R10K、R100K)各1个;5. 电容(C10uF、C100nF)各1个;6. 面包板 1个;7. 导线若干;8. 5V电源 1个。
四、实验内容与步骤1. 零输入响应实验(1)搭建RC电路,电阻R取100KΩ,电容C取10uF;(2)打开电源,使电容充电至5V;(3)断开电源,观察电容电压随时间的变化,并记录数据;(4)重复实验多次,确保数据的准确性。
2. 零状态响应实验(1)搭建RC电路,电阻R取100KΩ,电容C取10uF;(2)打开电源,使电容放电;(3)观察电容电压随时间的变化,并记录数据;(4)重复实验多次,确保数据的准确性。
3. 完全响应实验(1)搭建RC电路,电阻R取100KΩ,电容C取10uF;(2)打开电源,使电容充电至5V,然后断开电源;(3)观察电容电压随时间的变化,并记录数据;(4)重复实验多次,确保数据的准确性。
4. 方波激励实验(1)搭建RC电路,电阻R取100KΩ,电容C取10uF;(2)使用函数信号发生器输出频率为1kHz,峰峰值为5V的方波信号;(3)观察电容电压随时间的变化,并记录数据;(4)重复实验多次,确保数据的准确性。

实验四一阶电路响应研究1.一. 实验目的通过实验, 掌握用简单的R-C一阶电路观测零输入响应、零状态响应和完全响应的实验方法。
2.学习电路时间常数的测量方法。
3.掌握有关微分电路和积分电路的的概念。
二. 实验仪器设备仿真软件平台(Multisim 10);硬件基础电路实验箱。
双踪示波器、直流稳压电源、万用表、直流电流表、电压表。
三. 实验原理一阶电路的零输入响应零状态响应和完全响应分别按指数规律衰减和增长, 其变化的快慢决定于电路的时间常数τ, 实验电路如图4-1所示。
四. 实验内容1..Multisi.平台上连接电路并进行瞬态分析观.R.低通和高通一阶电路响应,记录.形;根据所绘出的响应曲线求出时间常数.,与理论计算值进行比较.2.以下内容要求先进行仿真实验, 然后在实验室物理平台上按以下步骤完成实验。
3.连接一个能观测零输入响应、零状态响应和完全响应的电路图(参考图4-1)。
分别观测该电路的零输入响应、零状态响应和完全响应的动态曲线。
a.零输入响应先连接K2.K3, 使+5V直流电源对电容C 充电, 当充电完毕后, 断开K3 连接K4, 用示波器观测Uc(t)的变化。
b. 零状态响.先连接K4, 使电容两端的电压放电完毕, 然后断开K4 连接K3.K1, 用示波器观测15V直流电压向电容C的充电过程。
c. 完全响.五.先连接K4, 使电容两端电压通过R-C回路放电, 一直到零为止。
然后连接K3.K2, 使5V电源向电容充电, 待充电完毕后, 将短路帽连接K1, 使15V 电源向电容充电, 用示波器观测Uc(t)的完全响应。
六.3.用示波器观.R.低通一阶电路的响应.用信号发生器输出的方波来模拟阶跃激励信号, 即利用方波输出的上升沿作为零状态响应的正阶跃激励信号;利用方波的下降沿作为零输入响应的负阶跃激励信号。
只要选择方波的.复周期远大于电路的时间常.., 一般要求方波的周.T>10., 那么电路在这样的方.序列脉冲信号的激励下, 它的响应就和直流电接通与断开的过渡过程是基本相同的. 观.R.低通一阶电路的响应;改.R.(R=10.., C=0.01..), 输入方波信号...=3..f=1K..), 在示波器的屏幕上观察到激励与响应的变化规律, 请测算出时间..., 并用方格纸.1:.的比例描绘波形。
一阶动态电路响应实验报告一阶动态电路响应实验报告引言:动态电路是电子学中的基础实验之一,通过对电路中的电流和电压的变化进行观察和分析,可以更好地理解电路的特性和响应。
本实验旨在研究一阶动态电路的响应特性,通过实验数据的分析,探索电路中的电流和电压的变化规律。
实验目的:1. 研究一阶动态电路的响应特性。
2. 掌握实验仪器的使用方法,如示波器、信号发生器等。
3. 学习数据采集和分析的方法。
实验原理:一阶动态电路是由电容和电阻组成的简单电路,其特点是电流和电压的变化具有指数衰减的趋势。
当电路中的电容充电或放电时,电流和电压的变化可以用指数函数来描述。
实验步骤:1. 搭建一阶动态电路实验电路,包括电容、电阻和信号发生器。
2. 将示波器连接到电路中,用于观察电流和电压的变化。
3. 设置信号发生器的频率和振幅,观察电路中电流和电压的响应。
4. 记录实验数据,包括电流和电压的变化情况。
5. 对实验数据进行分析,绘制电流和电压的变化曲线。
实验结果与分析:根据实验数据,我们可以得到一阶动态电路中电流和电压的变化曲线。
通过观察和分析曲线,我们可以得出以下结论:1. 在电容充电时,电流和电压的变化呈指数衰减的趋势,随着时间的增加,电流和电压逐渐趋于稳定。
2. 在电容放电时,电流和电压的变化也呈指数衰减的趋势,但是其衰减速度比充电时要快。
3. 电容的充电和放电时间常数与电阻和电容的数值有关,可以通过实验数据计算得出。
实验结论:通过本次实验,我们研究了一阶动态电路的响应特性,了解了电容充电和放电过程中电流和电压的变化规律。
实验结果表明,一阶动态电路中的电流和电压变化可以用指数函数来描述,而电容的充放电时间常数与电阻和电容的数值有关。
实验总结:本次实验通过实际操作和数据分析,深入理解了一阶动态电路的响应特性。
同时,我们也掌握了实验仪器的使用方法,如示波器和信号发生器。
通过实验的过程,我们不仅加深了对电路特性的理解,还培养了数据采集和分析的能力。
一阶动态电路响应实验报告-回复本个实验通过测试电路中的电压变化来研究一阶动态电路响应的特性。
在试验中,我们使用了一个RC 电路作为模型来研究电路中的电压变化,通过测量过渡过程中的电压变化和时间,进一步确定电路的时间常数和响应特性。
通过实验数据的分析,我们得出了电路的时间常数和阶跃响应曲线。
【关键词】一阶动态电路、响应特性、时间常数、阶跃响应曲线【实验目的】1. 了解一阶动态电路的基本原理和特性。
2. 掌握一阶动态电路的测试方法。
3. 通过实验验证一阶动态电路的时间常数和响应特性。
【实验原理】1. 一阶动态电路的基本原理一阶动态电路是一种简单的电路,它包含一个电阻和一个电容器。
电容器可以存储电能,电阻可让电容器内的电压平稳地释放。
该电路的特性是,当电路上有电压变化时,电容器内储存的电能会在一段时间内逐渐释放,直到电容器内的电荷完全消耗。
2. 一阶动态电路的响应特性一阶动态电路的响应特性可以通过两个参数来描述:时间常数和阶跃响应曲线。
时间常数是指电路中电容器放电至原电压的63.2% 所需的时间。
阶跃响应曲线则是电路输入突变信号时输出电压随时间的变化曲线。
【实验器材】示波器1 台、函数信号发生器1 台、电源1 台、电阻箱1 台、电容器1 台、万用表1 台【实验步骤】1. 按图1 连接RC 电路。
2. 将示波器和函数信号发生器分别接入电路。
3. 在函数信号发生器上设置一个方波信号,其幅度为5V,频率为1kHz。
4. 打开电源并调整函数信号发生器的幅度和频率,使得输入信号的幅度和频率符合实验要求。
5. 用示波器观察电路的输入和输出波形,并记录数据。
6. 分析数据,并绘制阶跃响应曲线。
7. 根据数据计算电路的时间常数,并与实验值进行比较。
【实验数据】时间(ms) 电压(V)0 0.000.2 0.400.4 1.000.6 2.800.8 3.801.0 4.00【数据分析】通过实验测量结果,我们可以得到该电路的阶跃响应曲线(如图2 所示)。
一阶动态响应电路分析 Pleasure Group Office【T985AB-B866SYT-B182C-BS682T-STT18】
一、实验目的
1、研究一阶动态电路的零输入响应、零状态响应及完全响应的特点和规律。
掌握测量一阶电路时间常数的方法。
2、理解积分和微分电路的概念,掌握积分、微分电路的设计和条件。
3、用multisim 仿真软件设计电路参数,并观察输入输出波形。
二、实验原理
1、零输入响应和零状态响应波形的观察及时间常数τ的测量。
当电路无外加激励,仅有动态元件初始储能释放所引起的响应——零输入响应;当电路中动态元件的初始储能为零,仅有外加激励作用所产生的响应——零状态响应;在外加激励和动态元件的初始储能共同作用下,电路产生的响应——完全响应。
以一阶RC 动态电路为例,观察电路的零输入和零状态响应波形,其仿真电路如图1(a )所示。
(a ) (b )
图1 一阶RC 动态电路
方波信号作为电路的激励加在输入端,只要方波信号的周期足够长,在方波作用期间或方波间隙期间,电路的暂态响应过程基本结束(τ52/≥T )。
故方波的正脉宽引起零状态响应,方波的负脉宽引起零输入响应,方波激励下的)(t u i 和)(t u o 的波形如图1(b )所示。
在)2/0(T t ,∈的零状态响应过程中,由于T <<τ,故在2/T t =时,电路已经达到稳定状态,即电容电压S o U t u =)(。
由零状态响应方程
可知,当2/)(S o U t u =时,计算可得τ69.01=t 。
如能读出1t 的值,则能测出该电路的时间常数τ。
2、RC 积分电路
由RC 组成的积分电路如图2(a )所示,激励)(t u i 为方波信号如图2(b )所示,输出电压)(t u o 取自电容两端。
该电路的时间常数2
T RC >>=τ(工程上称10倍以上关系为远远大于或远远小于关系。
),故电容的充放电速度缓慢,在方波的下一个下降沿(或上升沿)到来时,充放电均未达到稳态,输出波形如图2(c )所示,为近似三角波,三角波的峰值E <<'E 。
故R t u R t u t i i R )()()(≈=,因而⎰⎰
≈==dt t u RC dt t i C t u t u i c o )(1)(1)()(,所以输出电压近似地与输入电压的积分成正比。
图1
3、RC 微分电路
由RC 组成的微分电路如图3(a )所示,激励)(t u i 为方波信号如图3(b )所示,输出电压)(t u o 取自电阻两端。
该电路的时间常数2
T RC <<=τ,故电容的充放电速度非常快,在方波的下一个下降沿(或上升沿)到来时,电容电压在很短的时间内已充放电完成,并早已达到稳态,输出波形如图3(c )所示,为周期窄脉冲。
因而dt
t du RC dt t du RC
t Ri t u t u i C R o )()()()()(≈===,所以输出电压近似地与输入电压的微分成正比。
图3
三、仿真实验内容
1、在图1(a )中,已知nF C k R 1010=Ω=、。
在multisim 仿真软件中连接电路,并由函数信号发生器输出Hz f V V p p 10005000.4-==-,的方波信号。
利用双踪示波器同时观察)(t u i 和)(t u o 的波形,并在示波器上测量τ值,并与理论τ值进行比较。
2、根据积分电路形成条件,选择合适的R 、C 参数,组成如图2(a )所示的积分电路,其中)(t u i 为V V p p 0.4=-、kHz f 1=的方波。
在双踪示波器中同时观察)(t u i 和)(t u o 的波形。
3、根据微分电路形成的条件,选择合适的R 、C 参数,组成如图3(a)所示的微分电路,其中)(t u i 为V V p p 0.4=-、kHz f 1=的方波。
在双踪示波器中同时观察)(t u i 和)(t u o 的波形。
四、思考题
1、什么样的电信号可以作为一阶RC 电路零输入响应、零状态响应和完全响应的激励信号
答: 阶跃信号可作为RC 一阶电路零输入响应激励源;脉冲信号可作为RC 一阶电路 零状态响应激励源;正弦信号可作为RC 一阶电路完全响应的激励源,
2、当电容具有初始值时,RC 电路在阶跃激励下是否会出现没有暂态的现象,为什么 答:要看电容电压的初始值大小及极性,只有在电容初始电压的极性、大小完全与突加激励相同的条件下,才不会出现过渡暂态变化。
3、在研究方波激励积分电路的响应时,由于T >>τ,使得响应波形)(t u C 在2/T 时间内无法达到稳态值,故不能通过实验方法测量τ值。
但在积分电路的响应波形中包含了时间常数τ的信息,应用什么方法测量τ值
答:由RC 组成的积分电路如图2(a )所示,激励 )(t u i 为方波信号如图2(b )所示,输出电压 取自电容两端。
该电路的时间常数2T RC >>=τ (工程上称10倍以上关系为远远大于或远远小于关系。
),故电容的充放电速度缓慢,在方波的下一个下降沿(或上升沿)到来时,充放电均未达到稳态,输出波形如图2(c )所示,为近似三角波,三角波的峰值 。
故R t u R t u t i i R )()()(≈= ,因而⎰⎰≈==dt t u RC dt t i C t u t u i c o )(1
)(1)()( ,所以
输出电压近似地与输入电压的积分成正比。
答: R=τ/C;τ=RC
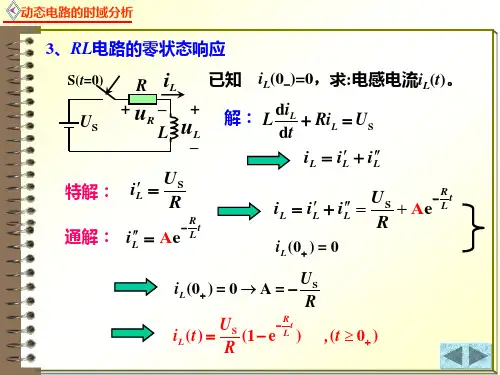
4、若将一阶RC 电路改为一阶RL 电路,对于方波激励,电路的响应波形又会怎样
答:若将一阶R 搜索C 电路改为一阶RL 电路,对于方波激励,电路的响应波形又会怎样由三角波变成尖脉冲。
5、能否用RL 电路设计积分或微分电路,如果能,电路参数设计需满足什么条件 答: 积分电路:τ>>T ,τ很大,则i 充电速度越来越慢)(0t u = )(u t R = )(t Ri ≈⎰dt t u L R
i )( 因此输出信号电压近似于输入信号的电压的积分成正比,输入信号为方波信号时,输出信号电压为三角波信号。
附上电感仿真图。