复数的几何意义(学生版)

复数的几何意义是什么复数的定义复数是形如a+bi的数。

式中a，b为实数，i是一个满足i=-1的数，因为任何实数的平方不等于-1，所以i不是实数，而是实数以外的新的数。

在复数a+bi中，a称为复数的实部，b称为复数的虚部，i称为虚数单位。

当虚部等于零时，这个复数就是实数;当虚部不等于零时，这个复数称为虚数，虚数的实部如果等于零，则称为纯虚数。

由上可知，复数集包含了实数集，因而是实数集的扩张。

复数常用形式z=a+bi叫做代数式。

我们把形如z=a+bi(a、b均为实数)的数称为复数。

其中，a称为实部，b称为虚部，i称为虚数单位。

当z的虚部b=0时，则z为实数;当z的虚部b≠0时，实部a=0时，常称z为纯虚数。

复数域是实数域的代数闭包，即任何复系数多项式在复数域中总有根。

复数是由意大利米兰学者卡当在16世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。

复数的四则运算公式复数运算法则有：加减法、乘除法。

两个复数的和依然是复数，它的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。

复数的加法满足交换律和结合律。

此外，复数作为幂和对数的底数、指数、真数时，其运算规则可由欧拉公式e^iθ=cos θ+i sin θ(弧度制)推导而得。

加法法则：复数的加法按照以下规定的法则进行：设z1=a+bi，z2=c+di是任意两个复数，则它们的和是 (a+bi)+(c+di)=(a+c)+(b+d)i。

两个复数的和依然是复数，它的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。

复数的加法满足交换律和结合律，即对任意复数z1，z2，z3，有： z1+z2=z2+z1;(z1+z2)+z3=z1+(z2+z3)。

减法法则：复数的减法按照以下规定的法则进行：设z1=a+bi，z2=c+di是任意两个复数，则它们的差是 (a+bi)-(c+di)=(a-c)+(b-d)i。

两个复数的差依然是复数，它的实部是原来两个复数实部的差，它的虚部是原来两个虚部的差。

复数及其运算一、课堂目标1．熟练掌握复数的相关概念及其几何意义并能熟练运用在解题中．2．熟练掌握复数代数形式的四则运算并会运用在解题中．3．掌握实系数一元二次方程两根的关系并会应用在解题中．4．理解复数的三角形式并能进行相关运算．二、知识讲解1. 复数的概念知识精讲（1）复数的概念形如的数叫复数.其中叫做虚数单位.（）规定：①复数中，把称为实部，称为虚部.②全体复数所形成的集合叫做复数集.一般用字母表示.即.③复数通常可以用字母表示，记作，这一表示形式称为复数的代数形式.（2）复数的分类已知复数①当时，则，为实数；特别地，当，且时，为实数.②当时，为虚数；特别地，当，且时，为纯虚数.（3）复数的相等规定：如果两个复数的实部和虚部分别相等，那么我们就说这两个复数相等.若..知识点睛（1）复数的分类归纳：（2）且（3）一般地，两个复数只能判断是否相等，不能比较大小（只有两复数均为实数时才比较大小）复数实数虚数纯虚数非纯虚数经典例题1.的实部是，虚部是．A.B.或C.D.2.复数与复数相等，则实数的值为（）巩固练习3.已知，则，．经典例题（1）（2）（3）4.已知复数，当实数为何值时，为实数．为虚数．为纯虚数．A.或B.或C.D.5.若复数，则实数的值是（）巩固练习6.设（），当时，为实数；当时，为纯虚数．2. 复数的几何意义知识精讲（1）几何意义（一）——复平面内容：复数复平面内的点对几何意义（一）的解释，如下图：一方面，根据复数相等的定义，复数被它的实部与虚部唯一确定，即复数被有序实数对唯一确定；另一方面，有序实数对在平面直角坐标系中对应着唯一的点.因此，可以在复数集与平面直角坐标系的点集之间建立一一对应关系，即：复数复平面内的点.这个建立了直角坐标系来表示复数的平面叫做复平面，轴叫做实轴，轴叫做虚轴．（2）共轭复数①概念：一般地，如果两个复数的实部相等，而虚部互为相反数，则称这两个复数互为共轭复数.复数的共轭复数记为，因此，当时，有.②在复平面内，表示两个共轭复数的点关于实轴对称；反之，如果表示两个复数的点在复平面内关于实轴对称，则这两个复数互为共轭复数.知识点睛要注意的地方：（1）“虚轴上的点都表示纯虚数”这种说法是错误的，原点必须除外；（2）复平面内各象限内的点均表示虚数；（3）复平面内点的坐标是，而不是.经典例题A. B.C. D.7.已知复数，则复平面内对应的点的坐标为（）．A. B.C.D.8.已知在复平面内对应的点在第二象限，则实数的取值范围是（）．巩固练习A.第一象限B.第二象限C.第三象限D.第四象限9.复数，则在复平面内对应的点所在象限为（ ）．A. B.C.D.10.在复平面内，复数对应的点的坐标为（ ）．经典例题A.B.C.D.11.若复数的共轭复数是（）．A. B.C.D.12.在复平面内，复数对应的点是，则复数的共轭复数（ ）．巩固练习A.第一象限 B.第二象限C.第三象限D.第四象限13.设，则在复平面内对应的点位于（ ）．经典例题14.满足下列条件的复数对应的点的集合分别是什么图形？．巩固练习15.满足下列条件的复数对应的点的集合分别是什么图形？．知识精讲（2）几何意义（二）——复数的向量表示内容：复数平面向量对几何意义（二）的解释，如下图：因为平面直角坐标系中的点能唯一确定一个以原点为始点、为终点的向量，所以复数也可用向量来表示，这样一来也就能在复数集与平面直角坐标系中，以为始点的向量组成的集合之间建立一一对应关系，即：复数平面向量.知识精讲（3）复数的模一般地，向量的长度称为复数的模（或绝对值），复数的模长用表示，因此.特别地：①当时，②一般地，两个互为共轭复数的模相等，即经典例题A.B. C. D.16.已知为虚数单位，则（）．巩固练习A. B. C. D.17.设为虚数单位，则复数的模（）．经典例题18.若复数满足，则的最大值是．巩固练习19.设复数满足条件，那么的最大值是．3. 复数的运算——加减法知识精讲（1）复数的加法运算法则设，是任意两个复数，则有：．（2）复数的减法运算法则①复数的相反数：一般地复数记作，并规定②设，是任意两个复数，则有：知识点睛（1）加法的运算规律：交换律：结合律：（2）关于复数的模的结论经典例题20.若（，是虚数单位），则的值为．21.设为虚数单位，复数，，则．巩固练习22.复数，其中是虚数单位，则复数的虚部是．23.已知复数，满足：，则的值为．4. 复数的运算——乘除法知识精讲复数的乘法运算法则①乘法运算法则：设，是任意两个复数，则有：②的次方：个相同的复数相乘时，称为的次方（或的次幂），并记作.知识点睛（1）复数的乘法运算律对于任意的，有==（2）复数的乘方运算律即对于任何复数及正整数、，有、、经典例题24.是虚数单位，若复数是纯虚数，则实数的值为．25.若，，其中为虚数单位，且，则．巩固练习26.设复数满足行，且是纯虚数，则．经典例题A. B.C.D.27.复数等于（）．巩固练习28.复数．知识精讲复数的除法运算法则①除法运算法则：设，是任意两个复数②复数的倒数：一般地，给定复数，称为的倒数.除以的商也可以看成与的倒数之积.知识点睛同实数类似，可以定义非零复数的次幂与负整数次幂，即当为非零复数且是正整数时，规定：经典例题A. B.C. D.29.若(其中为虚数单位)，则复数的虚部是（）．30.已知复数（为虚数单位），则．巩固练习31.设复数满足（是虚数单位），则复数的虚部为．5. 实数系一元二次方程在复数范围内的解集知识精讲设一元二次方程为.当时，方程有两个不相等的实数根当时，方程有两个相等的实数根引入复数后，当时，方程有两个不相等的虚数根可以发现这两个虚数根是一对共轭复数.、、且知识点睛一元二次方程的两个共轭虚数根同样满足一元二次方程中根与系数的关系，即引入复数后，在复数集中，实系数的二次三项式总可以分解成两个一次因式的乘积，即经典例题A. B.C. D.32.若关于的实系数一元二次方程的一个根为，则这个一元二次方程可以是（ ）．巩固练习33.若是实系数一元二次方程的一个根，则．6.复数三角形式知识精讲（1）复数的三角形式复数可表示为，称为复数的三角形式．是复数的模．是以轴的非负半轴为始边，向量所在射线为终边的角，称作复数的辐角.显然，任何一个非零复数的辐角都有无穷多个，而且任意两个辐角之间都相差的整数倍，并且在范围内的辐角的值称为复数的辐角主值，记作．经典例题A.B.C.D.34.已知，则复数的三角形式为（）．巩固练习（1）（2）（3）35.将下列复数表示为三角形式：知识精讲（2）复数乘法运算的三角表示及其几何意义①乘法运算的三角表示设，，．即两个复数相乘，积的模等于各复数的模的积，积的辐角等于各复数的辐角的和．②几何意义两个复数相乘时，如下图，先分别画出对应的向量，然后把向量绕点按逆时针方向旋转角，再把它的模变为原来的倍，得到向量，表示的复数就是积，这就是复数乘法的几何意义.知识点睛（1）复数乘法的几何意义可归纳为：模相乘，辐角相加（2）根据上述两个复数三角形式的乘法几何意义，可以推广到有限个复数的三角形式相乘，特别的，如果，则知识精讲（3）复数除法运算的三角表示及其几何意义①除法运算的三角表示设，，．即两个复数相除，商的模等于被除数的模除以除数的模所得的商，商的辐角被除数的辐角减去除数的辐角所得的差．②几何意义与乘法类似，还能得到两个复数相除的几何意义，例如，任意一个复数除以，从向量的角度来说，就相当于把这个复数对应的向量绕原点沿顺时针方向旋转.经典例题36.设，，则．巩固练习37.计算．11三、思维导图你学会了吗？画出思维导图总结本节课所学吧！四、出门测A.B. C. D.38.在复平面内，若所对应的点在第二象限，则实数的取值范围是（ ）．A.的虚部为B.的共轭复数为C.D.在复平面内对应的点在第三象限内39.已知复数，则下列说法正确的是（ ）．40.已知复满足（其中为虚数单位），则 ．。

b
OZ : a bi
a
x
环节二:一一对应，构建复数几何意义
我们知道在实数内：a 表示点 A 到原点的距离，同理，我们来思考一下：
z 表示什么？
y
Z : a bi
b
a
x
环节二:一一对应，构建复数几何意义
任务四：类比实数，猜想 z 表示的涵义
z 也表示的是点 Z 到原点的距离，也就是有向线段（向量） OZ 的长度（我们也称作向量的模）
复数集 C 中的数与复平面内的点按如下方式建立了一一对应关系
复数 z a bi(a,b R)
一一对应
有序实数对 ( a, b) 一一对应点 Z (a, b)
复平面中的点 Z (a, b) 是复数 z 的
几何表示
除原点外，
虚轴上的点
都表示纯虚
数.
虚轴
y
b
O
复平面
Z : a bi
实轴
x
实轴上的点都表示实数.
复数 z a bi(a,b R)
一一对应
点 Z (a, b) 一一对应 向量 OZ
向量 OZ 是复数 z 的另一种
y
b
OZ : a bi
几何表示
a
之后我们也将利用复数与向量之间一一对应
的关系，从几何的角度阐述复数的加法与乘
法。至此，复数理论才比较完整和系统地建
立起来了。
x
环节二:一一对应，构建复数几何意义
z a bi(a,b R) 的模，记作 z 或者 a bi ，且 z
a2＋b2
4.共轭复数
两个复数的实部 相同
，虚部互为
互为相反数
叫做互为共轭复数.复数 z 的共轭复数记做

跟踪训练2 在复平面内，O是原点，向量OA对应的复数为2＋i. (1)如果点A关于实轴的对称点为点B，求向量OB对应的复数； (2)如果(1)中的点B关于虚轴的对称点为点C，求点C对应的复数．
∴ቊx
− y
2==1，3x，解得ቊx
= −1， y = 1.
4．在复平面内，复数1＋i和1＋3i分别对应向量OA和OB，其中O为 坐标原点，则|AB|＝____2____．
解析：因为复数1＋i与1＋3i分别对应向量OA和OB，所以向量OA＝(1，1)，OB ＝(1，3)，
所以AB＝OB − OA＝(0，2)，所以|AB|＝2.
向量OZ的长度叫做复数z＝a＋bi的模，记作__|z_|_或__|_a＋__b_i_| _，且|a
＋bi|＝ a2 + b2.
知识点二 共轭复数 1．定义 如果两个复数的实部___相__等___，而虚部_互__为__相_反__数__，则这两个复数 叫做互为共轭复数． 2．表示 复数z的共轭复数用zത表示，即当z＝a＋bi(a，b∈R)时，则zത＝a－bi.
跟踪训练1 在复平面内，若复数z＝(m2－m－2)＋(m2－3m＋2)i对 应点：(1)在虚轴上；(2)在第二象限；(3)在直线y＝x上，分别求实数m 的值或取值范围．
解析：复数z＝(m2－m－2)＋(m2－3m＋2)i的实部为m2－m－2，虚部为m2－3m
＋2.
(1)由题意得m2－m－2＝0，
解得m＝2或m＝－1.
(3)复数z1>z2的充要条件是|z1|>|z2|.( × )
解析：错误．两个复数不一定能比较大小，但两个复数的模总能比较大小．
2．(多选)复数z＝cos
θ＋isin
θ(i为虚数单位)其中θ∈

复数的概念及复数的几何意义复数是数学中一种特殊的数形式，由实数和虚数组成。

在复数形式中，虚数单位i满足i²=-1、一个典型的复数可以表示为a+bi，其中a是实部，b是虚部。

复数的几何意义可以通过使用复平面来解释。

复平面是由实数轴和虚数轴组成的平面，将复数表示为平面上的点。

实部对应于横坐标，虚部对应于纵坐标。

根据这个表示法可以将复数表示为平面上的点。

实部和虚部可以是任意实数，因此复数在平面上可以表示为平面上的任意点。

平面上的坐标点(a,b)对应于复数a+bi。

平面上的原点(0,0)对应于复数0，纵坐标为0的点(0,b)对应于纯虚数bi，而横坐标为0的点(a,0)对应于纯实数a。

复数的运算可以通过在复平面上进行向量运算来实现。

两个复数的加法就是将两个向量叠加在一起，而减法就是将一个向量从另一个向量中减去。

乘法可以通过将复数旋转和缩放来实现。

复数的模可以用勾股定理推导得出：对于复数a+bi，它的模等于√(a²+b²)，表示为，a+bi。

模是复数的长度或距离原点的距离。

两个复数的模的乘积等于它们的乘积的模，即，a+bi， * ，c+di， = ，(a+bi)(c+di)。

复数的共轭是将虚部取负得到的，即a-bi是复数a+bi的共轭。

共轭复数在复平面上呈镜像关系，共轭对称于实轴。

复数的实部是自身的共轭，虚部取负是自身的共轭。

通过使用复数，可以解决许多实数范围内无法解决的问题。

例如，求根公式中的虚数单位i是由复数域推导而来。

复数也广泛应用于工程学、物理学和信号处理等领域。

实际上，电路和信号可以使用复数进行建模和分析。

总之，复数是数学中重要的概念之一，它由实数和虚数组成，并可以通过复平面表示。

复数的几何意义在于将复数表示为平面上的点，实部对应于横坐标，虚部对应于纵坐标。

复数可以进行向量运算，包括加法、减法、乘法和取共轭。

复数的模是其到原点的距离，模的乘积等于乘积的模。

复数的共轭是虚部取负得到的。

[跟踪训练 2]
1、在复平面内,A,B,三点对应的复数分别为1,2＋i,－1＋2i. （1）求向量 ―A→B ，―A→C ，―B→C 对应的复数； （2）若ABCD为平行四边形,求D对应的复数．
解析（1）设 O 为坐标原点，由复数的几何意义知： ―O→A ＝(1,0)，―O→B ＝(2,1)，―O→C ＝(－1,2)， 所以―A→B ＝―O→B －―O→A ＝(1,1)， ―A→C ＝―O→C －―O→A ＝(－2,2)，―B→C ＝―O→C －―O→B ＝(－3,1)， 所以―A→B ，―A→C ，―B→C 对应的复数分别为 1＋i，－2＋2i，－
[跟踪训练 1]
1、实数 x 取什么值时，复平面内表示复数 z＝x2＋x－6 ＋(x2－2x－15)i 的点 Z： (1)位于第三象限； (2)位于直线 x－y－3＝0 上．
解析 因为 x 是实数，所以 x2＋x－6，x2－2x－15 也是实数．
x2＋x－6<0，
(1)当实数 x 满足
即－3<x<2 时，点 Z 位于第
自主预习,回答问题
阅读课本70-72页,思考并完成以下问题
1、复平面是如何定义的,复数的模如何求出？ 2、复数与复平面内的点及向量的关系如何？复数的模是实 数还是虚数？
要求：学生独立完成,以小组为单位,组内可商量,最终选出代表回答问 题。
知识清单
1．复平面
2．复数的几何意义
(1)复数 z＝a＋bi(a，b∈R) 2复数 z＝a＋bia，b∈R
x2－2x－15<0，
三象限．
(2)当实数 x 满足(x2＋x－6)－(x2－2x－15)－3＝0，即 3x＋6＝0，
x＝－2 时，点 Z 位于直线 x－y－3＝0 上．

复数的几何意义是什么高中数学会学到复数，有关复数的几何意义大家知道吗?下面是由小编小编为大家整理的“复数的几何意义是什么”，仅供参考，欢迎大家阅读。

1、复数z=a+bi 与复平面内的点(a,b)一一对应2、复数z=a+bi 与向量OZ一一对应,其中Z点坐标为(a,b)1、复数的运算：复数的加法法则：设z1=a+bi，z2=c+di是任意两个复数。

两者和的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。

两个复数的和依然是复数。

复数的乘法法则：把两个复数相乘，类似两个多项式相乘，结果中i2=-1，把实部与虚部分别合并。

两个复数的积仍然是一个复数。

复数除法定义：满足的复数叫复数a+bi除以复数c+di的商。

运算方法：将分子和分母同时乘以分母的共轭复数，再用乘法法则运算。

2、我们把形如z=a+bi(a,b均为实数)的数称为复数，其中a称为实部，b称为虚部，i称为虚数单位。

当z的虚部等于零时，常称z为实数;当z的虚部不等于零时，实部等于零时，常称z为纯虚数。

复数域是实数域的代数闭包，即任何复系数多项式在复数域中总有根。

复数是由意大利米兰学者卡当在十六世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。

1、数学上的复数(1)复数的定义数集拓展到实数范围内,仍有些运算无法进行.比如判别式小于0的一元二次方程仍无解,因此将数集再次扩充,达到复数范围.定义：形如z=a+bi的数称为复数(complex number),其中规定i为虚数单位,且i^2=i*i=-1(a,b 是任意实数)我们将复数z=a+bi中的实数a称为虚数z的实部(real part)记作Rez=a实数b称为虚数z的虚部(imaginary part)记作 Imz=b.易知：当b=0时,z=a,这时复数成为实数;当a=0且b≠0时 ,z=bi,我们就将其称为纯虚数.复数的集合用C表示,显然,R是C的真子集复数集是无序集,不能建立大小顺序.(2)复数的四则运算法则：若复数z1=a+bi,z2=c+di,其中a,b,c,d∈R,则z1±z2=(a+bi)±(c+di)=(a±c)+(b±d)i,(a+bi)•(c+di)=(ac-bd)+(bc+ad)i,(a+bi)÷(c+di)=(ac+bd)/(c^2+d^2) +((bc-ad)/(c^2+d^2))i。

此类问题可根据复数的实部与虚部 应满足的条件列出方程(组)，通过 解方程(组)或不等式(组)求解.
跟踪训练1 求实数m分别取何值时，复数z＝(m2－m－2)＋ (m2－3m＋2)i(m∈R)对应的点Z满足下列条件： (1)在复平面内的x轴上方；
解 ∵点Z在x轴上方， ∴m2－3m＋2>0，解得m<1或m>2.
例2 在复平面内的长方形ABCD的四个顶点中，点A，B，C对
应的复数分别是2＋3i,3＋2i，－2－3i，求点D对应的复数.
解 记O为复平面的原点， 由题意得O→A＝(2,3)，O→B＝(3,2)，O→C＝(－2，－3). 设O→D＝(x，y)，则A→D＝(x－2，y－3)，B→C＝(－5，－5). 由题意知，A→D＝B→C，所以xy－－23＝＝－－55，， 即xy＝＝－－32，， 故点D对应的复数为－3－2i.
D.4
解析 ∵z＝(x＋1)＋(x－3)i，x∈R， ∴|z|＝ x＋12＋x－32＝ 2x2－4x＋10 ＝ 2x－12＋8≥ 8＝2 2(当且仅当 x＝1 时取等号). ∴|z|的最小值为 2 2.
(2)已知复数 z1＝x2＋ x2＋1i，z2＝(x2＋a)i，对于任意 x∈R 均有|z1|>|z2| 成立，则实数 a 的取值范围是___－__1_，__12_ __.
知识梳理
1.建立了直角坐标系来表示复数的平面叫做复平面，x轴叫做实轴， y轴叫做 虚轴 ，实轴上的点都表示 实数 ；除了 原点 外，虚轴上的 点都表示 纯虚数 . 2.复数集C中的数和复平面内所有的点组成的集合是 一一对应 的， 即复数z＝a＋bi ←一――一――对――应→ 复平面内的点Z(a，b)，这是复数的一种 几何意义.
2.方法归纳：待定系数法、数形结合. 3.常见误区：虚数不能比较大小，虚 数的模可以比较大小.

复数的几何意义在数学中，我们经常会遇到复数的概念和使用。

虽然复数在代数学中有着重要的作用，但它们在几何学中也具有深远的意义。

本文将探讨复数在几何学中的意义，并展示它们在平面几何中的应用。

1. 复数的定义复数是由一个实数和一个虚数组成的数，通常表示为"a+bi"的形式，其中a是实部，bi是虚部，而i是虚数单位，满足i^2 = -1。

复数可以用平面上的点来表示，实部对应点的x坐标，虚部对应点的y坐标。

2. 复数的模和参数复数的模表示复数到原点的距离，可以使用勾股定理来计算，即模=√(a^2 + b^2)。

复数的参数表示复数与正实轴之间的夹角，可以使用反三角函数来计算，即参数=arctan(b/a)。

3. 复数的几何表示复数可以用向量来表示，向量的起点为原点，终点为该复数对应的点。

因此，复数的几何表示就是平面上的一个向量。

通过调整实部和虚部的数值，可以得到不同的向量。

4. 复数的加法和减法复数的加法可以看作是向量的相加，即将两个复数的向量相加，得到一个新的向量。

减法可以看作是向量的相减，即将两个复数的向量相减，得到一个新的向量。

这两个操作在平面几何中对应着向量的平移。

5. 复数的乘法和除法复数的乘法可以看作是向量的旋转和缩放，即将一个复数的向量旋转一定角度，并将向量的长度乘以一个因子，得到一个新的向量。

除法可以看作是向量的反向旋转和缩放，即将一个复数的向量旋转一定角度，并将向量的长度除以一个因子，得到一个新的向量。

6. 复数的共轭复数的共轭表示将复数的虚部取相反数，保持实部不变。

共轭的几何意义是将复数表示的向量关于实轴反射得到的新向量。

7. 复数在平面几何中的应用复数在平面几何中有广泛的应用。

例如，可以使用复数来表示平移、旋转和缩放等变换。

复数的乘法和除法可以用来进行向量的旋转和缩放操作。

此外，复数还可以表示平面上的点，通过复数的运算可以得到点之间的距离和夹角等信息。

总结：复数在几何学中有着重要的意义，可以用来表示平面上的向量和点。

时，原有的加法与乘法的运算律(包括交换律、 结合律和分配律)仍然成立。
形如a+bi（a,b∈ R）的数叫做复数.
其中i是虚数单位.
全体复数所成的集合叫做复数集，用字母C表示 .
新课探究
1.复数的代数形式：通常用字母 z 表示，即
zab(iaR,bR)
i 实部 虚部 其中 称为虚数单位。
练一
练 说出下列复数的实部和虚部：
若a, b, c, d R,
a c
a bi c di b d
练习 2.
⑴已知 x y x 2y i 2x 5 3x y i
求实数 x, y 的值. x 3, y 2
⑵ 若3 10i y 2 i x 1 9i,
求实数 x, y 的值. x 1, y 1
知识引入
2．“a=0”是“复数a+bi (a , b∈R)所对应的点在
虚轴上”的（ ）C。
(A)必要不充分 (B)充分不必要条件
(C)充要条件
(D)不充分不必要条件
例3 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所 对应的点位于第二象限，求实数m取值范围。
解：由mm22
m m
6 2
0 0
答案：无数个；图形:以原点为圆心, 半径为5的圆
(3)满足3<|z|<5(z∈C)的复数z对应的点在 复平面上将构成怎样的图形？
答案：图形:以原点为圆心, 半径3至5的圆环内
小结
• 练习3、 • 求适合下列条件的复数z在复平面上表示
的图形．
• (1)2≤|z|<3； • (2)z＝x＋yi，x<0，y>0，且x2＋y2<9.
实数可以用数轴上的点来表示。

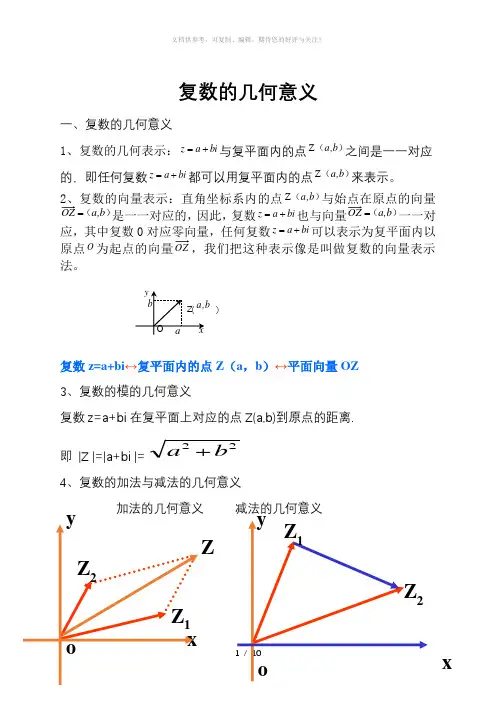
复数的几何意义一、复数的几何意义1、复数的几何表示：bi a z +=与复平面内的点）（b ,a Z 之间是一一对应的，即任何复数bi a z +=都可以用复平面内的点）（b ,a Z 来表示。

2、复数的向量表示：直角坐标系内的点）（b ,a Z 与始点在原点的向量）（b ,a OZ =是一一对应的，因此，复数bi a z +=也与向量）（b ,a OZ =一一对应，其中复数0对应零向量，任何复数bi a z +=可以表示为复平面内以原点O 为起点的向量OZ ，我们把这种表示像是叫做复数的向量表示法。

复数z=a+bi ↔复平面内的点Z （a ，b ）↔平面向量OZ 3、复数的模的几何意义复数z=a+bi 在复平面上对应的点Z(a,b)到原点的距离. 即 |Z |=|a+bi |=22b a +4、复数的加法与减法的几何意义加法的几何意义 减法的几何意义)ZZ 2Z1yz 1z 2≠0时， z 1+z 2对应的向量是以OZ 1、OZ 2、为邻边的平行四边形OZ 1ZZ 2的对角线OZ ， z 2-z 1对应的向量是Z 1Z 2 5、 复数乘法与除法的几何意义z 1=r 1（cos θ1+i sin θ1） z 2=r 2（cos θ2+i sin θ2）①乘法：z=z 1· z 2=r 1·r 2 [cos(θ1+θ2)+i sin(θ1+θ2)]如图：其对应的向量分别为oz oz oz 12→→→显然积对应的辐角是θ1+θ2 < 1 > 若θ2 > 0 则由oz 1→逆时针旋转θ2角模变为oz 1→的r 2倍所得向量便是积z 1·z 2=z 的向量oz →。

< 2 >若θ2< 0 则由向量oz 1→顺时针旋转θ2角模变为r 1·r 2所得向量便是积z 1·z 2=z 的向量oz →。

为此，若已知复数z 1的辐角为α，z 2的辐角为β求α+β时便可求出z 1·z 2=z a z 对应的辐角就是α+β这样便可将求“角”的问题转化为求“复数的积”的运算。

3
4
（3）这个方程可以写成 |z-(-2)|-|z-2|=2，所以表示到 两个定点F1(-2,0)，F2(2,0)距离 差2a等于2的点的轨迹，这个轨 迹是双曲线右半支．
x y 即双曲线： 1（x>0） 1 3
2
2
例4：△ABC的三个顶点对应的 复数分别是z1,z2,z3，若复数z满 足 |z-z1|=|z-z2|=|z-z3| ， 则 z 对应的点为△ABC的（ D ） A. 内心； B．垂心； C．重心； D．外心；
例1：设z∈C，满足下列条件的点Z的集 合是什么图形？ （1）|z|=4；（2）2≤|z|≤4．
解：（1）|z|=4表示到原点距离为4的点．所 以z表示的点Z构成一个半径为4的圆． （2）表示一个圆环．由于|z|的几何意义是点 Z到原点的距离，所以2≤|z|≤4表示到原点距 离大于等于2，小于4的点所构成的图形．
解：（1）方程可以看成 |z-(1+i)|=|z-(-2-i)|， 表示的是到两个定点A(1,1)和 B(-2,-1)距离相等的动点轨迹．所 以是线段AB的的垂直平分线。 即：直线6x+4y+3=0。
（2）方程可以看成 |z-(-i)|+|z-i|=4，表示的是到两个 定点(0,-1)和(0,1)距离和等于4的动点 轨迹．因为点Z到两个定点的距离和 是常数4，并且大于两点(0,-1)，(0,1) 间的距离2，所以满足方程的动点轨 迹是椭圆． 2 2 x y 即椭圆： 1
例 7 ：在复平面上 A 、 B 两点对应的 复数分别是 1 和 i ，复数 z 在直线 AB 上运动，求复数 z2 对应的点的轨迹。
解：设z=a+bi,(a,b∈R) 由题意，直线 AB 的方程是： x+y=1 ， ∵复数z在直线AB上运动，∴a+b=1， 再设z2对应的点为P(x,y) ∴z2=x+yi=(a+bi)2=(a2-b2)+2abi =(a-b)+2abi x a b 由复数相等的条件，得： y 2 ab 2 消去b,得y=(1-x ), 所以，复数z2对应的点的轨迹 是抛物线 y=(1-x2)。

1 / 13.1.3 复数的几何意义一、基础过关1．复数z ＝3＋i 3对应的点在复平面第几象限( ) A ．一 B ．二 C ．三 D ．四2．当0<m<1时，z ＝(m ＋1)＋(m －1)i 对应的点位于( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3．在复平面内，复数6＋5i ，－2＋3i 对应的点分别为A ，B.若C 为线段AB 的中点，则点C 对应的复数是 ( )A ．4＋8iB ．8＋2iC ．2＋4iD ．4＋i4．已知复数z ＝a ＋bi(a 、b ∈R )，当a ＝0时，复平面内的点z 的轨迹是( ) A ．实轴 B ．虚轴 C ．原点 D ．原点和虚轴5．已知复数z ＝a ＋3i 在复平面内对应的点位于第二象限，且|z|＝2，则复数z 等于( )A ．－1＋3iB ．1＋3iC ．－1＋3i 或1＋3iD ．－2＋3i6．若复数(－6＋k 2)－(k 2－4)i(k ∈R )所对应的点在第三象限，则k 的取值范围是________________．二、能力提升7．若θ∈(3π4，5π4)，则复数(cos θ＋sin θ)＋(sin θ－cos θ)i 在复平面内所对应的点在 ( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限8．复数z ＝icos θ，θ∈[0,2π)的几何表示是( ) A ．虚轴 B ．虚轴除去原点C ．线段PQ ，点P ，Q 的坐标分别为(0,1)，(0，－1)D ．C 中线段PQ ，但应除去原点9．复数z ＝log 123＋ilog 3 12对应的点位于复平面内的第______象限． 10．若复数z 1＝1－i ，z 2＝3－5i ，则复平面上与z 1，z 2对应的点Z 1与Z 2的距离为________．11．复数z ＝a 2－1＋(a ＋1)i(a ∈R )是纯虚数，则|z|＝______.12．当实数m 为何值时，复数z ＝(m 2－8m ＋15)＋(m 2＋3m －28)i 在复平面内的对应点：(1)位于第四象限； (2)位于x 轴负半轴上； (3)在上半平面(含实轴)．13．已知复数z 对应的向量为OZ →(O 为坐标原点)，OZ →与实轴正向的夹角为120°且复数z 的模为2，求复数z.三、探究与拓展14．(1)满足条件|z －i|＝|3＋4i|的复数z 在复平面上对应点的轨迹是( )A ．一条直线B ．两条直线C ．圆D ．椭圆 (2)已知复数(x －2)＋yi(x ，y ∈R )的模为3，求y x的最大值．。

2.复平面内向量对应的复数可以通过向量的坐标运算求得.
3.一个向量不管怎么平移，它所对应的复数是不变的，但其起点与终点对应的复
数可能改变.
3.已知复数 2 + − 2 + ( 2 − 3 + 2)( ∈ )是4 − 20的共轭复数，求的值.
2

解：由题意得，4 − 20的共轭复数为，则 2 + − 2 = 4，
或不等式(组)求解.
2.(1)向量1 对应的复数是5 − 4，向量2 对应的复数是−5 + 4，则1 + 2 对
应的复数是（ ）.
A.−10 + 8
B.10 − 8
C.0
D.10 + 8
答案：C.
(1)由复数的几何意义，得1 = (5, −4)，2 = (−5,4)，
数与复平面内的点按如下方式建立了一一对应关系
复数 = +
(, ).
这是复数的一种几何意义.
一一对应
复平面内的点
思考2：在平面直角坐标系中，每一个平面向量都可以用一个有序实数对来表示，
l
而有序实数对与复数是一一对应的.你能用平面向量来表示复数吗？
如图，设复平面内的点表示复数，连接，显然向量由点唯一确定；反过来，点
即|| = | + | = 2 + 2 ，其中， ∈ .
如果 = 0，那么 = + 是一个实数，它的模就等于||(的绝对值).
例2 设复数z1＝4＋3i，z2＝4－3i.
(1) 在复平面内画出复数z1，z2对应的点和向量；
(2) 求复数z1，z2的模，并比较它们的模大小.
答案：D.
(2)由复数的几何意义，得 = (2, −3)， = (−3,2)，

复数专题第4讲 利用复数几何意义求与模有关的最值问题一、复数的几何意义每个复数，有复平面内唯一的一个点和它对应；反过来，复平面内的每一个点，有唯一的一个复数与它对应.复数集C 中的数与复平面内的点建立了一 一对应的关系，复数z =a +bi 在复平面内的对应点Z(a,b)二、复数模的几何意义1、向量OZ⃗⃗⃗⃗⃗ 的模叫做复数z =a +bi 的模或绝对值，记作|z |或|a +bi |， 即|z |=|a +bi |=√a 2+b 2，其中a 、b ∈R ，|z |表示复平面内的点Z (a,b )到原点的距离；2、|z 1−z 2|的几何意义：复平面中点Z 1与点Z 2间的距离，如右图所示。

示例：|z +(1+2i)|表示：点Z 到点(−1,−2)的距离小结：复数的几何意义是复平面内两点之间的距离公式，若z =x +yi ，则|z −(a +bi)|表示复平面内点(x,y)与点(a,b)之间的距离，则|z −(a +bi)|=r 表示以(a,b)为圆心，以r 为半径的圆上的点.三、圆外一点到圆上一点的距离最值问题如图所示，点P 在圆O 上运动，在圆上找一点P 使得PA 最小（大）如图，当P 为OA 连线与圆O 交点时，PA 最小，最小为OA −r ；当P 在AO 延长线与圆O 交点P′时，PA 最大，最大为OA +r题型一 与复数有关的轨迹例z 1＝3＋i ，z 2＝－12＋32i. 设z ∈C ，满足条件|z 2|≤|z |≤|z 1|的点Z 的轨迹是什么图形？例2.已知复数z 满足|z |2－2|z |－3＝0，则复数z 对应点的轨迹为( )A ．一个圆B ．线段C ．两点D ．两个圆1.若复数z 满足|z －i|≤2(i 为虚数单位)，则z 在复平面内所对应的图形的面积为________．2.（多选）|(3+2i )−(1+i)|表示( )A ．点()3,2与点()1,1之间的距离B ．点()3,2与点()1,1--之间的距离C ．点()2,1到原点的距离D ．坐标为()2,1--的向量的模3.满足条件|z －2i|＋|z ＋1|＝5的点的轨迹是( )A ．椭圆B ．直线C ．线段D ．圆4.在复平面内，已知定点M 与复数m =1+2i ，那个点Z 与复数z =x +yi ，问：满足不等式|z −m |≤2的点Z 的集合是什么图形？题型二 模长最值问题例1.已知复数z的模为2，则|z－i|的最大值为（）A．1 B．2 C． 5 D．3例2.已知|z|＝2，求|z＋1＋3i|的最大值和最小值．例3.若复数z满足|z＋3＋i|≤1，求|z|的最大值和最小值．1.已知复数z的模为1，则2z+的最大值为__________.2.已知复数z，且|z|＝1，则|z+3+4i|的最小值是________．3.若z C∈，且4z=，则1z i+-的取值范围是________.4.已知复数z满足等式1i1z--=，则3z-的最大值为______5.若z C∈且342z i++≤，则z的取值范围为__________．6.若cos sinz iθθ=+(R iθ∈，是虚数单位)，则22z i--的最小值是（）A. C.1 D.。

3．3复数的几何意义[对应学生用书P43]复平面的定义问题1：平面向量可以用坐标表示，试想复数能用坐标表示吗？提示：可以．问题2：试说明理由．提示：因复数z＝a＋b i(a，b∈R)与有序实数对(a，b)惟一确定，由(a，b)与平面直角坐标系点一一对应，从而复数集与平面直角坐标系中的点集之间一一对应．建立直角坐标系来表示复数的平面叫做复平面．x轴叫做实轴，y轴叫做虚轴，实轴上的点都表示实数；除原点外，虚轴上的点都表示纯虚数.已知复数z ＝a ＋b i(a ，b ∈R )．问题1：在复平面内作出复数z 所对应的点Z . 提示：如图所示．问题2：向量OZ u u u r和点Z 有何关系？提示：有一一对应关系．问题3：复数z ＝a ＋b i 与OZ u u u r有何关系？提示：也是一一对应．1．复数与点，向量间的对应关系2．复数的模复数z ＝a ＋b i(a ，b ∈R )对应的向量为OZ u u u r ，则OZ u u u r的模叫做复数z 的模(或绝对值)，记作|z |，且|z |＝|a ＋b i|＝a 2＋b 2.复数加减法的几何意义如图1OZ u u u r 、2OZ u u u u r分别与复数a ＋b i ，c ＋d i 对应．问题1：试写出1OZ u u u r 、2OZ u u u u r 及1OZ u u u r ＋2OZ u u u u r 、1OZ u u u r －2OZ u u u u r的坐标． 提示：1OZ u u u r ＝(a ，b )，2OZ u u u u r＝(c ，d )，1OZ u u u r ＋2OZ u u u u r ＝(a ＋c ，b ＋d )，1OZ u u u r －2OZ u u u u r＝(a －c ，b －d )． 问题2：向量1OZ u u u r ＋2OZ u u u u r 及1OZ u u u r －2OZ u u u u r所对应的复数分别是什么？提示：(a ＋c )＋(b ＋d )i 及(a －c )＋(b －d )i.1．复数加法的几何意义设向量1OZ u u u r ，2OZ u u u u r 分别与复数z 1＝a ＋b i ，z 2＝c ＋d i 对应，且1OZ u u u r 和2OZ u u u u r不共线．如图，以1OZ u u u r ，2OZ u u u u r为邻边画平行四边形OZ 1ZZ 2，则其对角线OZ所表示的向量OZ u u u r OZ u u u r就是复数(a ＋c )＋(b ＋d )i 对应的向量．2．复数减法的几何意义复数的减法是加法的逆运算，设1OZ u u u r ，2OZ u u u u r 分别与复数a ＋b i ，c ＋d i 相对应，且1OZ u u u r，2OZ u u u u r不共线，如图．则这两个复数的差z 1－z 2与向量1OZ u u u r －2OZ u u u u r (等于21Z Z u u u u r)对应，这就是复数减法的几何意义．3．设z 1＝a ＋b i ，z 2＝c ＋d i(a ，b ，c ，d ∈R )，则|z 1－z 2|＝(a －c )2＋(b －d )2，即两个复数的差的模就是复平面内与这两个复数对应的两点间的距离．1．复平面上点的横坐标表示复数的实部，点的纵坐标表示复数的虚部．2．表示实数的点都在实轴上，实轴上的点都表示实数，它们是一一对应的；表示纯虚数的点都在虚轴上，但虚轴上的点不都表示纯虚数，如原点表示实数0.3．在平面向量中，向量的加法、减法的几何解释同复数加法、减法的几何解释是相同的．[对应学生用书P44]复数的几何意义[例1] 实数x 分别取什么值时，复数z ＝x 2＋x －6＋(x 2－2x －15)i 对应的点Z 在下列位置？(1)第三象限；(2)第四象限；(3)直线x －y －3＝0上？[思路点拨] 利用复数与复平面内点之间的对应关系求解．若已知复数z ＝a ＋b i(a ，b ∈R )，则当a <0且b <0时，复数z 对应的点在第三象限；当a >0且b <0时，复数z 对应的点在第四象限；当a －b －3＝0时，复数z 对应的点在直线x －y －3＝0上．[精解详析] 因为x 是实数，所以x 2＋x －6，x 2－2x －15也是实数． 若已知复数z ＝a ＋b i ，则当a ＜0，且b ＜0时，复数z 对应的点在第三象限； 当a ＞0，且b ＜0时，复数z 对应的点在第四象限； 当a －b －3＝0时，复数z 对应的点在直线x －y －3＝0上．(1)当实数x 满足⎩⎪⎨⎪⎧x 2＋x －6＜0，x 2－2x －15＜0，即－3＜x ＜2时，点Z 在第三象限．(2)当实数x 满足⎩⎪⎨⎪⎧x 2＋x －6＞0，x 2－2x －15＜0，即2＜x ＜5时，点Z 在第四象限．(3)当实数x 满足(x 2＋x －6)－(x 2－2x －15)－3＝0， 即x ＝－2时，点Z 在直线x －y －3＝0上．[一点通] 按照复数集和复平面内所有的点组成的集合之间的一一对应关系，每一个复数都对应着一个有序实数对，只要在复平面内找出这个有序实数对所表示的点，就可根据点的位置判断复数的实部、虚部的取值．1．(湖北高考改编)在复平面内，复数 z ＝2i1＋i (i 为虚数单位)的共轭复数对应点位于第________象限．解析：z ＝2i1＋i ＝2i (1－i )(1＋i )(1－i )＝2i (1－i )2＝i ＋1的共轭复数为1－i ，对应的点为(1，－1)在第四象限．答案：四2．求当实数m 为何值时，复数z ＝(m 2－8m ＋15)＋(m 2＋3m －28)i 在复平面内的对应点分别满足下列条件：(1)位于第四象限； (2)位于x 轴的负半轴上．解：(1)由题意，知⎩⎪⎨⎪⎧m 2－8m ＋15>0，m 2＋3m －28<0，解得⎩⎪⎨⎪⎧m <3或m >5，－7<m <4.即－7<m <3.故当－7<m <3时，复数z 的对应点位于第四象限．(2)由题意，知⎩⎪⎨⎪⎧m 2－8m ＋15<0 ①m 2＋3m －28＝0 ②由②得m ＝－7或m ＝4. 因m ＝－7不适合不等式①， m ＝4适合不等式①， 所以m ＝4.故当m ＝4时，复数z 的对应点位于x 轴的负半轴上．复数模及其几何意义的应用[例2] 已知复数z 1＝3－i 及z 2＝－12＋32i.(1)求|z 1|及|z 2|的值并比较它们的大小；(2)设z ∈C ，满足|z 2|≤|z |≤|z 1|的点z 的集合是什么图形．[思路点拨] 由复数的模长公式求出|z 1|及|z 2|，然后比较大小；(2)根据点数模的几何意义画出图形．[精解详析] (1)|z 1|＝|3－i|＝(3)2＋(－1)2＝2， |z 2|＝⎪⎪⎪⎪－12＋32i ＝⎝⎛⎭⎫－122＋⎝⎛⎭⎫322＝1，所以|z 1|＞|z 2|.(2)由(1)知1≤|z |≤2，因为不等式|z |≥1的解集是圆|z |＝1上和该圆外部所有点组成的集合，不等式|z |≤2的解集是圆|z |＝2上和该圆内部所有点组成的集合，所以满足条件1≤|z |≤2的点Z 的集合是以原点O 为圆心，以1和2为半径的两圆所夹的圆环，并包括圆环的边界，如图所示．[一点通] (1)计算复数的模时，应先找出复数的实部和虚部，然后再利用模的公式进行计算，两个虚数不能比较大小，但它们的模可以比较大小．(2)复数的模表示该复数在复平面内对应点到原点的距离．3．(辽宁高考改编)复数z ＝1i －1的模为________． 解析：∵z ＝1－1＋i ＝－1－i (－1＋i )(－1－i )＝－1－i2＝－12－12i ，∴|z |＝ ⎝⎛⎭⎫－122＋⎝⎛⎭⎫－122＝22. 答案：224．已知z ＝3＋a i ，且|z －2|＜2，则实数a 的取值范围是________． 解析：∵z ＝3＋a i ，∴z －2＝1＋a i ， ∴|z －2|＝1＋a 2<2，即1＋a 2<4，∴a 2<3，即－3<a < 3. 答案：(－3，3)5．设z ∈C ，则满足条件|z |＝|3＋4i|的复数z 在复平面上对应的点Z 的集合是什么图形？ 解：法一：由|z |＝|3＋4i|得|z |＝5.这表明向量OZ u u u r的长度等于5，即点Z 到原点的距离等于5.因此满足条件的点Z 的集合是以原点O 为圆心，以5为半径的圆． 法二：设z ＝x ＋y i(x ，y ∈R )，则|z |2＝x 2＋y 2. ∵|3＋4i|＝5，∴由|z |＝|3＋4i|得x 2＋y 2＝25，∴点Z 的集合是以原点为圆心，以5为半径的圆．[例3] 已知▱OABC 的三个顶点O ，A ，C 对应的复数分别为0,3＋2i ，－2＋4i ，试求：(1) AO u u u r 表示的复数；(2) CA u u r表示的复数；(3)点B 对应的复数．[思路点拨] 点O ，A ，C 对应的复数――――――→向量的坐标表示AO u u u r ，CA u u r ，OBu u u r的坐标形式――――――→复数在复平面上与向量一一对应AO u u u r ，CA u u r ，OBu u u r 对应的复数[精解详析] (1)AO u u u r ＝－OA u u r ，故AO u u u r表示的复数为－(3＋2i)，即－3－2i. (2)CA u u r ＝OA u u r －OC u u u r ，故CA u u r表示的复数为(3＋2i)－(－2＋4i)＝5－2i. (3)OB u u u r ＝OA u u r ＋AB u u u r ＝OA u u r ＋OC u u ur ，故OB u u u r 表示的复数为(3＋2i)＋(－2＋4i)＝1＋6i ，即点B 对应的复数为1＋6i.[一点通] (1)根据复数的两种几何意义可知：复数的加、减运算可以转化为点的坐标运算或向量运算．(2)复数的加、减运算用向量进行时，同样满足平行四边形法则和三角形法则． (3)复数及其加、减运算的几何意义为数形结合思想在复数中的应用提供了可能．6．已知复数z 1＝2＋i ，z 2＝1＋2i 在复平面内对应的点分别为A 、B ，求AB u u u r对应的复数z ，z 在平面内对应的点在第几象限？解：z ＝z 2－z 1＝(1＋2i)－(2＋i)＝－1＋i ， ∵z 的实部－1<0，虚部1>0，∴复数z 在复平面内对应的点在第二象限内．7．在复平面内，点A 、B 、C 分别对应复数z 1＝1＋i ，z 2＝5＋i ，z 3＝3＋3i.以AB 、AC 为邻边作一个平行四边形ABDC ，求D 点对应的复数z 4及AD 的长．解：如图，由复数加减法的几何意义， AD u u u r ＝AB u u u r ＋AC u u ur ，即z 4－z 1＝(z 2－z 1)＋(z 3－z 1)． 所以z 4＝z 2＋z 3－z 1＝7＋3i.|AD |＝|z 4－z 1|＝|(7＋3i)－(1＋i)|＝|6＋2i|＝210.1．复数模的几何意义复数模的几何意义架起了复数与解析几何之间的桥梁，使得复数问题可以用几何方法解决，而几何问题也可以用复数方法解决(即数形结合法)，增加了解决复数问题的途径． (1)复数z ＝a ＋b i(a ，b ∈R )的对应点的坐标为(a ，b )，而不是(a ，b i)；(2)复数z ＝a ＋b i(a ，b ∈R )的对应向量OZ u u u r是以原点O 为起点的，否则就谈不上一一对应，因为复平面上与OZ u u u r相等的向量有无数个．2．复数的模(1)复数z ＝a ＋b i(a ，b ∈R )的模|z |＝a 2＋b 2；(2)从几何意义上理解，表示点Z 和原点间的距离，类比向量的模可进一步引申：|z 1－z 2|表示点Z 1和点Z 2之间的距离．[对应学生用书P45]一、填空题1．若OA u u r 、OB u u u r 对应的复数分别是7＋i,3－2i ，则|AB u u u r|＝________.解析：∵OA u u r ＝(7,1)，OB u u u r＝(3，－2)， ∴AB u u u r ＝OB u uu r －OA u u r ＝(－4，－3)，∴|AB u u u r|＝5.答案：52．(重庆高考改编)复平面内表示复数i(1－2i)的点位于第________象限． 解析：i(1－2i)＝2＋i 对应的点为(2,1)，位于第一象限． 答案：一3．若z ＋|z |＝2＋8i ，则z ＝________. 解析：法一：设z ＝a ＋b i(a ，b ∈R )， 则|z |＝a 2＋b 2，代入方程得a ＋b i ＋a 2＋b 2＝2＋8i.所以⎩⎪⎨⎪⎧a ＋a 2＋b 2＝2，b ＝8，解得⎩⎪⎨⎪⎧a ＝－15，b ＝8，所以z ＝－15＋8i.法二：原式可化为z ＝2－|z |＋8i ， ∵|z |∈R ，∴2－|z |是z 的实部． 于是|z |＝(2－|z |)2＋82，即|z |2＝68－4|z |＋|z |2，∴|z |＝17.代入z ＝2－|z |＋8i ，得z ＝－15＋8i. 答案：－15＋8i4．已知z 1＝2＋i ，z 2＝3＋a i(a ∈R )，若z 1＋z 2所对应的点在实轴上，则a ＝________. 解析：z 1＋z 2＝2＋i ＋3＋a i ＝5＋(a ＋1)i ，由z 1＋z 2所对应的点在实轴上可知a ＋1＝0，即a ＝－1. 答案：－15．(新课标全国卷Ⅰ改编)设z ＝11＋i ＋i ，则|z |＝________.解析：11＋i ＋i ＝1－i(1＋i )·(1－i )＋i ＝1－i 2＋i ＝12＋12i ，则|z |＝⎝⎛⎭⎫122＋⎝⎛⎭⎫122＝22. 答案：22二、解答题6．若复数z ＝(m 2＋m －2)＋(4m 2－8m ＋3)i(m ∈R )的共轭复数z 对应的点在第一象限，求实数m 的集合．解：由题意得z ＝(m 2＋m －2)－(4m 2－8m ＋3)i ，z 对应的点位于第一象限，所以有⎩⎪⎨⎪⎧ m 2＋m －2>0，－(4m 2－8m ＋3)>0，所以⎩⎪⎨⎪⎧m 2＋m －2>0，4m 2－8m ＋3<0，所以⎩⎪⎨⎪⎧m <－2或m >1，12<m <32，即1<m <32，故所求m 的集合为⎩⎨⎧m ⎪⎪⎭⎬⎫1<m <32. 7．在复平面内A ，B ，C 三点对应的复数分别为1,2＋i ，－1＋2i. (1)求AB u u u r ，BC u u ur ，AC u u u r 对应的复数；(2)判断△ABC 的形状；(3)求△ABC 的面积．解：(1)AB u u u r对应的复数为z B －z A ＝(2＋i)－1＝1＋i. BC u u u r对应的复数为z C －z B ＝(－1＋2i)－(2＋i)＝－3＋i.AC u u u r对应的复数为z C －z A ＝(－1＋2i)－1＝－2＋2i.(2)由(1)知|AB u u u r|＝|1＋i|＝2，|BC u u u r |＝|－3＋i|＝10，|AC u u u r |＝|－2＋2i|＝22， ∴|AB u u u r|2＋|AC u u u r |2＝|BC u u u r |2.故△ABC 为直角三角形．(3)S △ABC ＝12|AB u uu r |·|AC u u u r |＝12×2×22＝2.8．若z ∈C 且|z ＋2－2i|＝1，求|z －2－2i|的最小值．解：已知|z－(－2＋2i)|＝1中，z的对应点轨迹是以(－2,2)为圆心，1为半径的圆，|z－(2＋2i)|表示圆上的点与点(2,2)之间的距离，最小值为圆心与点(2,2)的距离减去半径，易得值为3.。

高中数学 必修第二册 RJ·A
典例剖析
一、 复数与复平面内的点对应
例1 已知复数z＝(a2－4)＋(2a－3)i，其中a∈R.当复数z在复平面内对应的点Z 满足下列条件时，求a的值(或取值范围). (1)Z在实轴上；
解 因为z＝(a2－4)＋(2a－3)i， 所以复数z在复平面内对应的点Z的坐标为(a2－4,2a－3). 若点Z在实轴上，则有2a－3＝0， 解得 a＝32.
∴复数z＝(3m－2)＋(m－1)i在复平面内对应的点位于第四象限.
高中数学 必修第二册 RJ·A
→ 3.在复平面内，O 为原点，向量OA对应的复数为－1＋2i，若点 A 关于直线
→ y＝－x 的对称点为 B，则向量OB对应的复数为
A.－2－i C.1＋2i
B.－2＋i D.－1＋2i
B解析 ∵A(－1,2)关于直线y＝－x的对称点为B(－2,1)， →
高中数学 必修第二册 RJ·A
(2)若复数z＝(m＋1)＋(m－2)i，其中m∈R，则复数z对应的点不可能位于
A.第一象限
B.第二象限
C.第三象限
D.第四象限
B解析 复数z对应的点为(m＋1，m－2).因为m＋1>m－2， 所以点(m＋1，m－2)不可能位于第二象限.
高中数学 必修第二册 RJ·A
0＋2 x0＝32， 若设 D(x0，y0)，则有
－32＋y0＝2，
x0＝3，
解得
故 D(3,7).
y0＝7，
→
→
→
方法二 由已知得OA＝(1,4)，OB＝(0，－3)，OC＝(2,0)，
→
→
所以BA＝(1,7)，BC＝(2,3)，
→→→
→
由平行四边形的性质得BD＝BA＋BC＝(3,10)，而OB＝(0，－3)，于是 D(3,7).