新人教版三角形面积计算公式新选

新人教版五年级上册《第5章多边形的面积》单元测试卷一、填空题1. 长方形面积公式是________，梯形面积公式是________，三角形面积公式是________，平行四边形面积公式是________．2. 一个三角形的底是8分米，高是12分米，它的面积是________平方分米；与它等底等高的平行四边形的面积是________平方分米。

3. 如图，在边长相等的五个正方形中，画了两个三角形。

如果三角形A的面积是45平方厘米，那么三角形B的面积是________平方厘米。

4. 一个平行四边形的底是7厘米，高是8厘米，面积是________平方厘米；与它等底等高的三角形的面积是________平方厘米。

5. 5平方米=________平方分米2000平方厘米=________平方分米。

6. 一个三角形的面积是40平方米，它的高是4米，它的底是________米。

7. 在长10厘米，宽7厘米的长方形纸片中剪去一个最大的三角形，这个三角形的面积是________平方厘米。

8. 如图阴影部分面积是15平方厘米，则平行四边形面积是________平方厘米。

9. 如果一个梯形的上底是a，下底是上底的3倍，高是上底的2倍，这个梯形的面积用字母表示是________．二、判断题．（对的打√，错的打×）边长是4厘米的正方形，它的周长和面积相等。

________．（判断对错）三角形的面积等于平行四边形面积的一半。

________．（判断对错）长方形和正方形的周长相等，它们的面积也一定相等。

________．（判断对错）两个完全一样的梯形可以拼成一个平行四边形。

________．（判断对错）两个三角形面积相等，底和高也一定相等。

________．（判断对错）三、选择题．平行四边形有________条高，三角形有________高。

A.1B.2C.3D．无数。

把平行四边形转化成长方形（如图），转化后的图形与原来的相比，它的（）A.面积和周长都没变B.面积变了，周长没变C.周长变了，面积没变D.无法确定两个完全一样的梯形不可能拼成的图形是（）A.长方形B.三角形C.平行四边形已知一个三角形的面积是60平方厘米，高是15厘米，求底的算式是（）A.60+15B.60÷15C.60÷15÷2D.60×2÷15如图中阴影部分的面积是24cm2，点A是平行四边形底边上的中点，则这个平行四边形的面积是()cm2．A.96B.48C.24D.12四、操作题．先画出如图中指定底边上的高，量出有关数据后再计算它的面积。

面积/周长计算公式1、长方形的周长=（长+宽）×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽 S=ab4、正方形的面积=边长×边长 S=a.a= a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高 S=ah7、梯形的面积=（上底+下底）×高÷2 S=（a＋b）h÷28、直径=半径×2 d=2r 半径=直径÷2 r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr10、圆的面积=圆周率×半径×半径Ѕ=πr11、长方体的表面积=（长×宽+长×高＋宽×高）×212、长方体的体积 =长×宽×高 V =abh13、正方体的表面积=棱长×棱长×6 S =6a14、正方体的体积=棱长×棱长×棱长 V=a.a.a= a15、圆柱的侧面积=底面圆的周长×高 S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr +2πrh=2π(d÷2)+2π(d÷2)h=2π(C÷2÷π) +Ch17、圆柱的体积=底面积×高 V=ShV=πr h=π(d÷2) h=π(C÷2÷π) h18、圆锥的体积=底面积×高÷3V=Sh÷3=πr h÷3=π(d÷2) h÷3=π(C÷2÷π)h÷319、长方体（正方体、圆柱体）的体积=底面积×高 V=Sh 最新文件仅供参考已改成word文本。

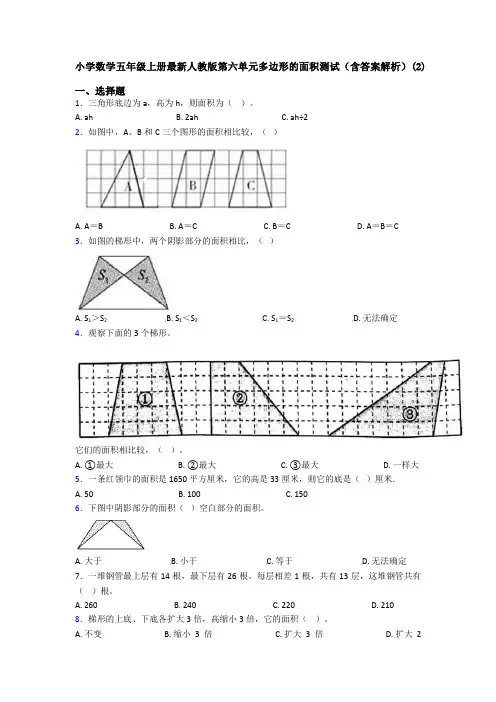
小学数学五年级上册最新人教版第六单元多边形的面积测试（含答案解析）(2)一、选择题1．三角形底边为a，高为h，则面积为（）。

A. ahB. 2ahC. ah÷22．如图中，A、B和C三个图形的面积相比较，（）A. A＝BB. A＝CC. B＝CD. A＝B＝C3．如图的梯形中，两个阴影部分的面积相比，（）A. S1＞S2B. S1＜S2C. S1＝S2D. 无法确定4．观察下面的3个梯形。

它们的面积相比较，（）。

A. ①最大B. ②最大C. ③最大D. 一样大5．一条红领巾的面积是1650平方厘米，它的高是33厘米，则它的底是（）厘米．A. 50B. 100C. 1506．下图中阴影部分的面积（）空白部分的面积。

A. 大于B. 小于C. 等于D. 无法确定7．一堆钢管最上层有14根，最下层有26根。

每层相差1根，共有13层，这堆钢管共有（）根。

A. 260B. 240C. 220D. 2108．梯形的上底、下底各扩大3倍，高缩小3倍，它的面积（）。

A. 不变B. 缩小3倍C. 扩大3倍D. 扩大29．如图，阴影部分的面积与空白部分的面积相比较，它们（）。

A. 相等B. 不相等C. 无法确定10．一个直角三角形，直角所对的边长是10厘米，其余两边分别是8厘米和6厘米，这个三角形的面积是（）平方厘米。

A. 40B. 30C. 2411．底和高分别相等的两个平行四边形（）。

A. 周长相等B. 面积相等C. 周长和面积都相等12．如图，在两个完全相同的长方形中各剪下一个三角形。

这两个三角形的面积相比（）A. A>BB. A<BC. A=BD. 不能确定二、填空题13．一个梯形上、下底之和是24分米，高是4分米，它的面积是________平方分米。

14．一个平行四边形的底是 4.8分米，高是 1.6分米，与它等底等高的三角形面积是________平方分米．15．一块三角形的交通标志牌，面积是35.1dm2，底是9dm．这个底对应的高是________dm．16．如图，两个完全一样的梯形拼成了一个平行四边形．梯形的上底为a，下底为b，高为h，则平行四边形的面积为________．17．如图，平行线中的三个图形，把它们的面积按从大到小的顺序排列是________>________>________。

2024年新课标人教版七年级下全册数学教案一、教学内容本节课选自2024年新课标人教版七年级下册数学教材第五章《三角形的初步认识》，具体内容包括：5.1三角形的定义及性质，5.2三角形的分类，5.3三角形的周长和面积。

二、教学目标1. 知识目标：使学生掌握三角形的定义，理解三角形的性质，掌握三角形的分类，掌握三角形周长和面积的计算方法。

2. 能力目标：培养学生运用三角形知识解决实际问题的能力，提高学生的空间想象力和逻辑思维能力。

3. 情感目标：激发学生对数学学习的兴趣，培养学生的合作意识和探究精神。

三、教学难点与重点重点：三角形的定义及性质，三角形的分类，三角形周长和面积的计算方法。

难点：三角形性质的理解，三角形面积公式的推导。

四、教具与学具准备教具：三角板、直尺、圆规、多媒体设备。

学具：三角板、直尺、圆规、练习本。

五、教学过程1. 导入：通过展示生活中的三角形实物，引导学生发现三角形的特征，从而引出本节课的主题。

2. 新课导入：（2）三角形的性质：引导学生通过画图、观察、思考，发现三角形的性质，如内角和等于180°等。

（3）三角形的分类：根据三角形的边长和角度，将三角形分为不等边三角形、等腰三角形、等边三角形、直角三角形等。

（4）三角形周长和面积的计算：通过实例讲解，引导学生掌握三角形周长和面积的计算方法。

3. 例题讲解：讲解典型例题，巩固所学知识，引导学生运用所学知识解决实际问题。

4. 随堂练习：设计有针对性的练习题，让学生当堂巩固所学知识。

六、板书设计1. 三角形的定义：由三条线段首尾顺次连接所围成的图形。

2. 三角形的性质：内角和等于180°，两边之和大于第三边等。

3. 三角形的分类：不等边三角形、等腰三角形、等边三角形、直角三角形等。

4. 三角形周长和面积的计算方法。

七、作业设计1. 作业题目：（3）应用题：运用三角形的周长和面积知识，解决实际问题。

2. 答案：见附页。

第6单元第2课时《三角形的面积》同步练习一、精挑细选。

1、一个三角形的底是4分米，高是2分米，它的面积是（）.A．2平方分米B．4平方分米C．1平方分米D．4分米2、在如图两条平行线间，三角形ABC、三角形DBC和三角形EBC的面积（）A．相等B．不相等 C．无法确定3、两个同底等高的三角形，它们的（）一定相等．A．形状B．面积C．周长4、一个三角形的高是6分米，面积是30平方分米，底是（）.A．6分米 B．12分米C．10分米D．5分米5、一个直角三角形的三条边分别是3厘米、4厘米、5厘米，这个直角三角形的面积是（）.A．10平方厘米B．7.5平方厘米C．12平方厘米 D．6平方厘米6、如图有甲乙丙三个面积相等的平行四边形，它们阴影部分的面积相比较（）.A．甲大B．乙大C．丙大D．相等7、一个三角形的底不变，如果高扩大4倍，那么它的面积（）.A．扩大4倍 B．扩大2倍 C．无法确定8、一个平行四边形的面积比与它等底等高的三角形面积大28平方厘米，则三角形的面积是（）平方厘米．A．28 B．14 C．42 D．569、三角形斜边上的高是（）厘米．A．20 B．24 C．2810、如图，梯形ABCD中共有8个三角形，其中面积相等的三角形有（）.A．1对 B．2对 C．3对 D．4对二、填一填、我最棒。

1、三角形的底是5分米，高是4分米．和它等底等高的平行四边形的面积是 .2、一个三角形与一个平行四边形的底和面积分别相等，已知三角形的高是6厘米．平行四边形的高是厘米.3、一个三角形，它的面积是24平方厘米，底是8厘米，高是厘米．4、把三角形的底和高都扩大到原来的3倍，则三角形的面积扩大到原来的倍.5、一个等边三角形的周长是12厘米，高是3.46厘米，它的面积是厘米².三、计算下面三角形的面积。

（1）（2）（3）四、解答题。

1、如图平行四边形的面积是36平方米，求阴影部分的面积．（单位：米）2、求阴影部分的面积（单位：cm）五、应用题。

新人教版五年级上册《第5章多边形的面积》单元测试卷（3）一、填空题（共7小题，每空3分，满分36分）1. 1900平方厘米=________平方米；4.31公顷=________平方米；5平方米8平方分米=________平方米=________平方分米。

2. 一个平行四边形的底是14厘米，高是9厘米，它的面积是________；与它等底等高的三角形面积是________．3. 一个梯形的上底是3米，下底2米，高2米，这个梯形的面积是________平方米；与它等上、下底之和等高的平行四边形的面积是________．4. 工地上有一堆钢管，横截面是一个梯形，已知最上面一层有2根，最下面一层有12根，共堆了11层，这堆钢管共有________根。

5. 一个三角形比与它等底等高的平行四边的面积少30平方厘米，则这个三角形的面积是________．6. 一个三角形的面积是45平方分米，底是5分米，高是________分米。

7. 一个等边三角形的周长是18厘米，高是3.6厘米，它的面积是________平方厘米。

二．我会判断是非（正确的在括号内画“√”，错误的画“×”）（每题3分，共15分）平行四边形的面积等于三角形面积的2倍。

________（判断对错）两个完全一样的梯形可以拼成一个平行四边形。

________．（判断对错）把一个长方形的木条框架拉成一个平行四边形，它的面积减少了。

________．（判断对错）两个三角形面积相等，底和高也一定相等。

________．（判断对错）三．“择优录取”，选一选．（每题3分，共9分）两个完全一样的锐角三角形可以拼成一（）A.长方形B.正方形C.平行四边形D.梯形把一个平行四边形任意分割成两个梯形，这两个梯形的（）相等。

A.高B.面积C.上、下底之和在如图中，平行线间的三个图形，它们的面积相比()A.平行四边形的面积大B.一样大C.三角形的面积大D.梯形的面积大四．我会求阴影部分的面积．（每题6分，共12分）我会求阴影部分的面积。

小学数学1--6年级公式大全1、每份数×份数＝总数; 总数÷每份数＝份数；总数÷份数＝每份数2、 1倍数×倍数＝几倍数；几倍数÷1倍数＝倍数；几倍数÷倍数＝1倍数3、速度×时间＝路程；路程÷速度＝时间；路程÷时间＝速度4、单价×数量＝总价；总价÷单价＝数量；总价÷数量＝单价5、工作效率×工作时间＝工作总量；工作总量÷工作效率＝工作时间；工作总量÷工作时间＝工作效率6、加数＋加数＝和；和－一个加数＝另一个加数7、被减数－减数＝差；被减数－差＝减数；差＋减数＝被减数8、因数×因数＝积；积÷一个因数＝另一个因数9、被除数÷除数＝商被除数÷商＝除数商×除数＝被除数小学数学图形计算公式1、正方形: C=周长、S=面积、a=边长周长＝边长×4 C=4a ；面积=边长×边长S=a×a2、正方体: V=体积 a=棱长表面积=棱长×棱长×6 S表=a×a×6 ；体积=棱长×棱长×棱长V=a×a×a3、长方形: C=周长、 S=面积、a=边长周长=(长+宽)×2 ；C=2(a+b)；面积=长×宽；S=ab4、长方体: V=体积、s=面积 a=长、b=宽、 h=高(1)表面积= (长×宽+长×高+宽×高)×2 、S=2(ab+ah+bh)(2)体积=长×宽×高、V=abh5、三角形: s=面积、 a=底、 h=高面积=底×高÷2 s=ah÷2 ；三角形高=面积×2÷底；三角形底=面积×2÷高6、平行四边形: s=面积、 a=底、 h=高面积=底×高 s=ah7、梯形:s=面积、 a=上底、 b=下底、 h=高面积=(上底+下底)×高÷2 s=(a+b)× h÷28、圆形:S=面积、 C=周长、圆周率=π、 d=直径、 r=半径(1)周长=直径×π=2×π×半径C=πd=2πr(2)面积=半径×半径×π9、圆柱体:v=体积、h=高、s=底面积、r=底面半径、c=底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高10、圆锥体:v=体积、 h=高、 s=底面积、 r=底面半径体积=底面积×高÷3和差问题的公式(和＋差)÷2＝大数；(和－差)÷2＝小数和倍问题和÷(倍数－1)＝小数小数×倍数＝大数(或者和－小数＝大数)差÷(倍数－1)＝小数小数×倍数＝大数(或小数＋差＝大数)植树问题1、非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数＝段数＋1＝全长÷株距－1全长＝株距×(株数－1)株距＝全长÷(株数－1)⑵如果在非封闭线路的一端要植树,另一端不要植树,那么: 株数＝段数＝全长÷株距全长＝株距×株数; 株距＝全长÷株数⑶如果在非封闭线路的两端都不要植树,那么:株数＝段数－1＝全长÷株距－1全长＝株距×(株数＋1); 株距＝全长÷(株数＋1) 2、封闭线路上的植树问题的数量关系如下株数＝段数＝全长÷株距全长＝株距×株数; 株距＝全长÷株数盈亏问题(盈＋亏)÷两次分配量之差＝参加分配的份数(大盈－小盈)÷两次分配量之差＝参加分配的份数(大亏－小亏)÷两次分配量之差＝参加分配的份数相遇路程＝速度和×相遇时间相遇时间＝相遇路程÷速度和速度和＝相遇路程÷相遇时间追及问题追及距离＝速度差×追及时间追及时间＝追及距离÷速度差速度差＝追及距离÷追及时间流水问题顺流速度＝静水速度＋水流速度逆流速度＝静水速度－水流速度静水速度＝(顺流速度＋逆流速度)÷2水流速度＝(顺流速度－逆流速度)÷2浓度问题溶质的重量＋溶剂的重量＝溶液的重量溶质的重量÷溶液的重量×100%＝浓度溶液的重量×浓度＝溶质的重量溶质的重量÷浓度＝溶液的重量利润与折扣问题利润＝售出价－成本利润率＝利润÷成本×100%＝(售出价÷成本－1)×100% 涨跌金额＝本金×涨跌百分比折扣＝实际售价÷原售价×100%(折扣＜1)利息＝本金×利率×时间税后利息＝本金×利率×时间×(1－2020长度单位换算1公里＝1千米；1千米=1000米；1米=10分米；1分米=10厘米；1米=100厘米；1厘米=10毫米面积单位换算1平方千米=100公顷；1公顷=10000平方米；1平方米=100平方分米； 1平方分米=100平方厘米； 1平方厘米=100平方毫米1公顷＝10000平方米；1亩＝666.666平方米体(容)积单位换算1立方米=1000立方分米；1立方分米=1000立方厘米；1立方厘米＝1000立方毫米1立方分米=1升；1立方厘米=1毫升；1立方米=1000升重量单位换算1吨=1000 千克；1千克=1000克；1千克=1公斤；1公斤 = 2市斤人民币单位换算1元=10角；1角=10分；1元=100分时间单位换算1世纪=100年；1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时；1时=60分；1分=60秒；1时=3600秒定义定理公式三角形的面积＝底×高÷2、公式S= a×h÷2正方形的面积＝边长×边长、公式S= a×a长方形的面积＝长×宽、公式S= a×b平行四边形的面积＝底×高、公式S= a×h梯形的面积＝(上底+下底)×高÷2、公式S=(a+b)h÷2内角和:三角形的内角和＝180度。

三角形的面积新课标解读与教材分析随着新课标教育改革的实施，数学教材中对于三角形的面积计算方式也有了一些更新和改进。

本文将对新课标下的三角形面积计算方法进行解读，并分析教材中相关内容的优缺点。

一、新课标解读在新课标中，三角形的面积计算方法得到了简化和优化。

过去，我们常使用的面积公式为：S = 1/2 ×底 ×高。

但在新课标中，这一公式被进一步拓展，考虑到了不仅仅是底和高，还涉及到了三角形的边长。

新课标中提出了两种计算三角形面积的方法。

第一种是通过三边长度直接计算，即使用海伦公式。

海伦公式的表达式为：S = √[p(p-a)(p-b)(p-c)]，其中p代表半周长，a、b、c代表边长。

这种方法适用于任意三角形，无需知道高或底边的情况。

第二种方法则是针对特殊情况，即已知底边和高的情况。

这时可以直接使用传统的面积公式：S = 1/2 ×底 ×高。

这种方法适用于已知底和高的等腰、直角三角形等特殊情况。

通过以上的新课标解读，我们可以看到，在教材中提供了不同的面积计算方式，以满足不同的题目需求。

二、教材分析在新课标的数学教材中，对于三角形的面积计算方法给予了较为详细的解释和举例，使学生能够更加深入地理解和掌握。

首先，教材通过引入海伦公式，将三角形面积计算和三边关系相结合，从而让学生了解到面积计算并不仅仅依赖于底和高这一简单的关系。

给出的计算公式和示例题目都能够清晰地展示这种计算方法的应用。

其次，教材中还介绍了特殊情况下的面积计算方法，针对已知底边和高的等腰、直角三角形等特殊情况，使学生能够对应用场景进行灵活运用，提高解题能力。

然而，在教材中对于面积计算的整体结构安排方面，还有一些可以改进的地方。

例如，可以增加一些实际生活中的例子，引导学生将数学知识应用到实际问题中。

这样有助于学生理解面积计算的实际意义，提高他们的学习兴趣。

另外，教材中可以进一步加强对于不同计算方法的比较和选择的讲解。

三角形的面积计算公式
三角形的面积计算公式：
1.已知三角形底a，高h，则 S＝ah/2
2.已知三角形三边a,b,c，则
（海伦公式）（p=(a+b+c)/2）
S=[p(p-a)(p-b)(p-c)]
=（1/4）[(a+b+c)(a+b-c)(a+c-b)(b+c-a)]
3.已知三角形两边a,b,这两边夹角C，则S＝1/2 * absinC
4.设三角形三边分别为a、b、c，内切圆半径为r
则三角形面积=(a+b+c)r/2
5.设三角形三边分别为a、b、c，外接圆半径为R
则三角形面积=abc/4R
6.S△=1/2 *
| a b 1 |
| c d 1 |
| e f 1 |
| a b 1 |
| c d 1 | 为三阶行列式,此三角形ABC在平面直角坐标系内A(a,b),B(c,d), C(e,f),这里ABC
| e f 1 |
选区取最好按逆时针顺序从右上角开始取，因为这样取得出的结果一般都为正值，如果不按这个规则取，可能会得到负
值，但不要紧，只要取绝对值就可以了，不会影响三角形面积的大小！
7.海伦--秦九韶三角形中线面积公式:
S=[(Ma+Mb+Mc)*(Mb+Mc-Ma)*(Mc+Ma-Mb)*(Ma+Mb-Mc)]/3 其中Ma,Mb,Mc为三角形的中线长.
8.根据三角函数求面积：
S= ab sinC=2R sinAsinBsinC= asinBsinC/2sinA
注:其中R为外切圆半径。

9.根据向量求面积：
S)= (|AB|*|AC|)-（AB*AC）。

最全面的三角形面积公式河北邯郸 贾敬堂一提到三角形面积公式，大家都知道。

① 已知三角形的底边长为a , 高为h ，则三角形面积S= 底 ⨯ 高 ÷2 2ah=B实际上，三角形面积公式太多啦，上面得公式是最基本的公式，根据条件不同，三角形面积公式也不同。

②已知三角形的周长为l ，内切圆半径为r ，则三角形面积2lr S =③已知三角形的三边长的乘积为L ，外接圆半径为R ，则三角形面积4L S R=④已知三角形AOB 中，向量OA a =，OB b =，则三角形面积S =。

此公式也适用于空间三角形求面积。

⑤已知在平面直角坐标系中，三角形ABC 的三顶点坐标分别为，11(,)A x y ，22(,)B x y ，33C(,)x y ,则三角形面积11223311121x y S x y x y =的绝对值12233113213212x y x y x y x y x y x y =++---。

特别地，当(0,0)C ，或经过平移后(0,0)C ，此时，三角形面积122112S x y x y =-。

⑥海伦（Heran ）公式，已知△ABC 中，1,,,()2AB c BC a CA b p a b c ====++，则三角形面积S我国宋朝时期也有类似的三角形面积公式，即秦九韶公式，也叫三斜求积公式。

S = ⑦已知三角形两边及夹角，则三角形面积公式为111sin sin sin 222S ab C bc A ca B ===⑧已知三角形两角及夹边，则三角形面积公式为222sin sin sin sin sin sin 2sin()2sin()2sin()c A B b A C a B C S A B A C B C ===+++⑨已知三角形两角A 、B 及其中一边的对边a ，则三角形面积公式为2sin()sin 2sin a A B B S A+=⑩已知空间三角形ABC 的顶点111222333(,,),(,,),(,,)A x y z B x y z C x y z 。