初三二次函数总复习

初中数学中考复习二次函数知识点总结归纳整理二次函数是中学数学中非常重要的一个内容，也是中考数学中的重点。

下面是对初中数学中考复习二次函数知识点的总结和归纳整理。

一、二次函数的定义1. 二次函数的一般形式：y = ax² + bx + c，其中a、b、c为常数，且a ≠ 0。

2.二次函数的图像为抛物线，开口方向与a的正负有关。

-当a>0时，抛物线开口向上。

-当a<0时，抛物线开口向下。

二、二次函数的性质1.对称轴：二次函数的对称轴与抛物线的开口方向垂直，其方程为x=-b/2a。

2.顶点：二次函数的顶点位于对称轴上，其坐标为（-b/2a,f(-b/2a)）。

-当a>0时，顶点是抛物线的最低点。

-当a<0时，顶点是抛物线的最高点。

3. 判别式：对于二次函数y = ax² + bx + c，其判别式Δ = b² -4ac表示方程ax² + bx + c = 0的根的情况。

-当Δ>0时，方程有两个不相等的实根。

-当Δ=0时，方程有两个相等的实根。

-当Δ<0时，方程没有实根。

4.单调性：-当a>0时，二次函数在对称轴左侧单调递增，右侧单调递减。

-当a<0时，二次函数在对称轴左侧单调递减，右侧单调递增。

三、二次函数的图像特征1.a的正负决定了抛物线的开口方向。

2.，a，的大小决定了抛物线的陡峭程度，a，越大抛物线越陡峭。

3.当b=0时，抛物线经过原点。

4.当c=0时，抛物线经过x轴。

5.当a>0时，函数值在顶点处取得最小值。

6.当a<0时，函数值在顶点处取得最大值。

四、二次函数的方程求解1. 解二次方程ax² + bx + c = 0的一般步骤：- 利用判别式Δ = b² - 4ac判断方程的根的情况。

-若Δ>0，方程有两个不相等的实根，可以用求根公式x₁=(-b+√Δ)/2a和x₂=(-b-√Δ)/2a求解。

二次函数知识点总结一、定义与定义表达式一般地，自变量x 和因变量y 之间存在如下关系： y =ax 2+bx +c （a ≠0），则称y 为x 的二次函数。

二、二次函数的三种表达式一般式：y =ax 2+bx +c （a ≠0）顶点式：y =a (x -h ) 2+k （a ≠0），此时抛物线的顶点坐标为P （h ，k ）交点式：y =a (x -x 1)(x -x 2)（a ≠0）仅用于函数图像与x 轴有两个交点时，x 1、x 2为交点的横坐标，所以两交点的坐标分别为A （x 1，0）和 B （x 2，0）），对称轴所在的直线为x=2x 21+ 注：在3种形式的互相转化中，有如下关系： h =-a 2b ，k =a 4b -4ac 2 ； x 1, x 2=a24ac -b b -2± ；x 1+x 2=-a 2b 三、二次函数的图像从图像可以看出，二次函数的图像是一条抛物线，属于轴对称图形。

四、抛物线的性质1．抛物线是轴对称图形，对称轴为直线 x = -a2b ，对称轴与抛物线唯一的交点是抛物线的顶点P 。

特别地，当b =0时，抛物线的对称轴是y 轴（即直线x =0）2．抛物线有一个顶点P ，坐标为P （-a 2b ，a 4b -4ac 2）。

当x =-a 2b 时，y 最值=a4b -4ac 2，当a >0时，函数y 有最小值；当a <0时，函数y 有最大值。

当-a 2b =0时，P 在y 轴上（即交点的横坐标为0）；当Δ= b 2-4ac =0时，P 在x 轴上（即函数与x 轴只有一个交点）。

3．二次项系数a 决定抛物线的开口方向和大小（即形状）。

当a ＞0时，抛物线开口向上；当a ＜0时，抛物线开口向下。

|a |越大，则抛物线的开口越小。

对于两个抛物线，若形状相同，开口方向相同，则a 相等；若形状相同，开口方向相反，则a 互为相反数。

4．二次项系数a 和一次项系数b 共同决定对称轴的位置，四字口诀为“左同右异”，即： 当对称轴在y 轴左边时，a 与b 同号（即ab ＞0）；当对称轴在y 轴右边时，a 与b 异号（即ab ＜0）。

2024年中考数学总复习：二次函数一．选择题（共25小题）1．抛物线y＝（x+1）2﹣1的对称轴是（）A．直线x＝0B．直线x＝1C．直线x＝﹣1D．直线y＝12．将抛物线y＝﹣x2+2向左平移2个单位，再向下平移3个单位，得到抛物线解析式为（）A．y＝﹣（x+2）2﹣1B．y＝﹣（x﹣2）2﹣1C．y＝﹣（x+2）2+5D．y＝﹣（x﹣2）2+53．已知二次函数y＝kx2+2x+1的图象与x轴有交点，则k的取值范围是（）A．k＜1且k≠0B．k≤1C．k≥1D．k≤1且k≠0 4．把抛物线y＝x2+bx+2的图象向右平移3个单位，再向上平移2个单位，所得到的图象的解析式为y＝x2﹣4x+7，则b＝（）A．2B．4C．6D．85．已知点（﹣3，y1），（2，y2），(−12，y3)都在函数y＝x2﹣1的图象上，则（）A．y2＜y1＜y3B．y1＜y3＜y2C．y1＜y2＜y3D．y3＜y2＜y1 6．二次函数y＝ax2+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x＝2，下列结论：①当x＞﹣1时，y的值随x值的增大而增大；②a﹣b+c＞0；③4a+b＝0；④9a+c＞3b；其中正确的结论是（）A．①B．②C．③D．④7．已知二次函数y＝3（x﹣1）2+k的图像上有三点A（√2，y1），B（3，y2），A（0，y3），则y1，y2，y3为的大小关系为（）A．y1＞y2＞y3B．y2＞y1＞y3C．y3＞y1＞y2D．y2＞y3＞y18．A(−12，y1)，B（1，y2），C（4，y3）三点都在二次函数y＝﹣（x﹣1）2+k的图象上，则y1，y2，y3的大小关系为（）A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y1＜y2D．y3＜y2＜y1第1页（共17页）。

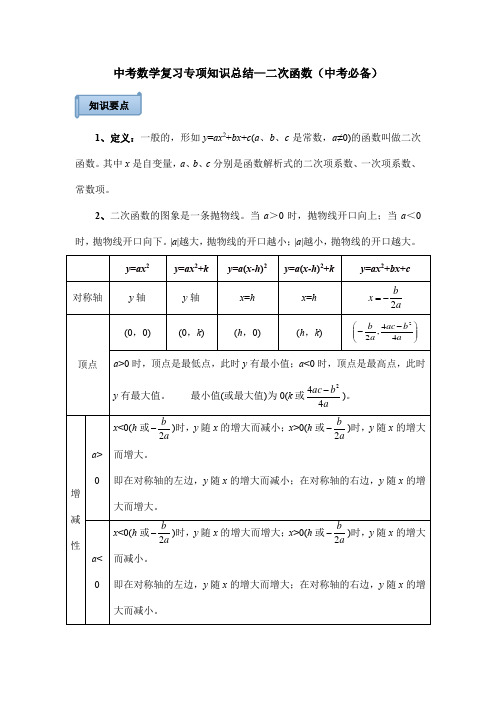
中考数学复习专项知识总结—二次函数（中考必备）1、定义：一般的，形如y=ax2+bx+c(a、b、c是常数，a≠0)的函数叫做二次函数。

其中x是自变量，a、b、c分别是函数解析式的二次项系数、一次项系数、常数项。

2、二次函数的图象是一条抛物线。

当a＞0时，抛物线开口向上；当a＜0时，抛物线开口向下。

|a|越大，抛物线的开口越小；|a|越小，抛物线的开口越大。

3、二次函数y=ax2+bx+c与一元二次方程ax2+bx+c=0的联系：(1)如果抛物线y=ax2+bx+c与x轴有公共点，公共点的横坐标是x0，那么当x=x0时，函数值是0，因此x=x0是方程ax2+bx+c=0的一个根；(2)抛物线与x轴的交点和一元二次方程的根的关系1、通过对实际问题的分析，体会二次函数的意义。

2、会用描点法画出二次函数的图象，通过图象了解二次函数的性质。

3、会用配方法将数字系数的二次函数的表达式化为y=a(x-h)2+k的形式，并能由此得到二次函数图象的顶点坐标，说出图象的开口方向，画出图象的对称轴，并能解决简单实际问题。

4、会利用二次函数的图象求一元二次方程的近似解。

1、二次函数的基本概念。

2、结合已知条件确定二次函数的表达式，利用待定系数法求二次函数的解析式。

3、根据二次函数的图象及性质解决相关问题，如不等式、一元二次方程。

4、二次函数图象的平移。

5、二次函数与实际问题，二次函数与综合问题(与几何、函数、方程等的综合)。

1、下列各点中，在函数y =-x 2图象上的点是（ ）A 、(-2，4)B 、(2，-4)C 、(-4，2)D 、(4，-2)2、二次函数y =(3m -2)x 2+mx +1的图象开口向上，则m 的取值范围是 。

3、抛物线21(3)52y x =---的开口方向 ，对称轴是 ，顶点坐标是 ，与x 轴的交点个数是 个。

4、二次函数21522y x x =+-的图象的顶点坐标是 。

5、二次函数y =2(x -1)2+5图象的对称轴和顶点P 的坐标分别是（ ） A 、直线x =-1，P(-1，5) B 、直线x =-1，P(1，5) C 、直线x =1，P(1，5) D 、直线x =1，P(-1，5) 6、把抛物线y =-4x 2向上平移2个单位，再向左平移3个单位，得到的抛物线是（ ）A 、y =-4(x +3)2+2B 、y =-4(x +3)2-2C 、y =-4(x -3)2+2D 、y =-4(x -3)2-27、在平面直角坐标系中，将二次函数y =-2(x -1)2-2的图象向左平移1个单位，再向上平移1个单位，则其顶点变为（ ）A 、（0,0）B 、（1，-2）C 、（0，-1）D 、（-2,1）8、二次函数y=(x-1)2+2的最小值是（）A、2B、1C、-1D、-29、已知二次函数y=3x2+2x+a与x轴没有交点，则a的取值范围是。

教材：初中数学九年级上册复习目标：1.理解二次函数的概念和特征。

2.掌握二次函数的基本性质和图像的特点。

3.熟练运用二次函数解决实际问题。

4.理解抛物线的性质及其与二次函数的关系。

一、概念复习1.二次函数：通过变量的平方项表达的函数。

2.顶点：二次函数图像的最高点或最低点，表示为（a，b）。

3.对称轴：二次函数图像的对称轴，表示为x=a。

4.开口方向：二次函数图像的开口方向，由二次项的系数决定。

二、性质复习1.零点：二次函数与x轴交点的横坐标。

2.判别式：用来判断二次函数的零点个数的式子。

当Δ=b^2-4ac＞0时，二次函数有两个不相等的零点。

当Δ=b^2-4ac=0时，二次函数有两个相等的零点。

当Δ=b^2-4ac＜0时，二次函数没有实数零点。

3.最大值与最小值：当二次函数开口向上时，最小值是顶点的纵坐标。

当二次函数开口向下时，最大值是顶点的纵坐标。

三、图像特点复习1.开口方向：当a＞0时，二次函数开口向上。

当a＜0时，二次函数开口向下。

2.对称轴：对称轴与顶点的横坐标相等。

3.零点：零点是二次函数与x轴交点的横坐标。

零点的个数由判别式Δ决定。

四、实际问题复习1.利用二次函数解决实际问题的步骤：（1）明确问题中有关条件。

（2）设出二次函数的表达式。

（3）求出二次函数的最值或零点。

（4）用解出的最值或零点回答问题。

2.举例：问题：商场的营业额可以用二次函数y=2x^2+3x+4来表示，其中x表示时间（以小时计），y表示营业额（以万元计）。

求该商场的最大营业额，并在什么时间实现。

解答：（1）根据题目，得到二次函数的表达式为y=2x^2+3x+4（2）通过求导数或将二次函数表示为顶点形式，得到该二次函数的顶点为（-3/4，23/8）。

（3）所以，该商场的最大营业额为23/8万元，实现时间为-3/4小时。

五、抛物线的性质复习1. 加入二次函数的f(x)=ax^2+bx+c。

若a＞0，抛物线开口向上；若a＜0，抛物线开口向下。

中考复习二次函数知识点总结二次函数是中考数学中的重要知识点之一、下面我将从函数的定义、图像特征、解析式以及一些常见题型进行总结，希望对中考复习有所帮助。

一、函数的定义：函数是数学中最基本的概念之一，它是描述两个集合之间对应关系的规则。

在二次函数中，我们通常用y来表示函数的值，用x表示自变量。

二、图像特征：1.开口方向：二次函数的图像在x轴上开口的方向可以通过二次项的系数（即a的正负性）来判断。

当a>0时，二次函数的图像开口向上；当a<0时，二次函数的图像开口向下。

2.对称轴：二次函数的图像总是关于一个垂直于x轴的直线对称。

这条直线称为二次函数的对称轴，它的方程为x=-b/(2a)。

3.顶点坐标：对称轴与二次函数图像的交点称为顶点，它的坐标为：(-b/(2a),f(-b/(2a)))4.单调性：当a>0时，二次函数图像在对称轴左侧递减，在对称轴右侧递增；当a<0时，二次函数图像在对称轴左侧递增，在对称轴右侧递减。

注意：二次函数的图像开口向上时，在对称轴上有一个最小值，反之开口向下时，在对称轴上有一个最大值。

三、解析式：一般情况下，二次函数的解析式可以写成：y=ax^2+bx+c，其中a、b、c为常数，且a≠0。

特殊情况下，二次函数的解析式还有以下两种形式：1.完全平方式：y=a(x-p)^2+q，其中p、q为常数。

此时，二次函数的对称轴的方程为x=p，顶点的坐标为(p,q)。

2.二次项因式可能性：y=a(x-h)(x-k)，其中h、k为常数。

此时，二次函数的对称轴的方程为x=(h+k)/2，顶点的坐标为((h+k)/2,a(h+k)/4)。

四、常见题型：1.求顶点坐标：根据二次函数的解析式，可以直接读出顶点的坐标。

2.求对称轴方程：根据二次函数的解析式，可以直接读出对称轴的方程。

3.求图像开口方向：判断二次项的系数a的正负性即可。

4.求单调性：根据图像特征可以判断。

5. 求零点：令y=0，解方程ax^2+bx+c=0即可。

初三数学期末复习二次函数一、二次函数概念：1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数．2. 二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2．⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项． 二、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质： a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质： 上加下减。

3. ()2y a x h =-的性质：左加右减。

4. ()2y a x h k =-+的性质：三、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”． 概括成八个字“左加右减，上加下减”． 方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a -=-=，．五、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）.画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a-．2. 当0a <时，抛物线开口向下，对称轴为2b x a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2bx a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2bx a =-时，y 有最大值244ac b a-．七、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）.注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大； ⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小． 2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴． ⑴ 在0a >的前提下，当0b >时，02ba-<，即抛物线的对称轴在y 轴左侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴；当0b <时，02ba->，即抛物线对称轴在y 轴的右侧． ⑵ 在0a <的前提下，结论刚好与上述相反，即 当0b >时，02ba->，即抛物线的对称轴在y 轴右侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴； 当0b <时，02ba-<，即抛物线对称轴在y 轴的左侧． 总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．ab 的符号的判定：对称轴abx 2-=在y 轴左边则0>ab ，在y 轴的右侧则0<ab ，概括的说就是“左同右异” 总结：3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正； ⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0； ⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负． 总结起来，c 决定了抛物线与y 轴交点的位置．总之，只要a b c ，，都确定，那么这条抛物线就是唯一确定的．二次函数解析式的确定：根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3. 已知抛物线与x 轴的两个交点的横坐标，一般选用两根式；4. 已知抛物线上纵坐标相同的两点，常选用顶点式．九、二次函数图象的对称二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y a x b x c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---； 2. 关于y 轴对称2y a x b x c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++； 3. 关于原点对称2y a x b x c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-；4. 关于顶点对称（即：抛物线绕顶点旋转180°）2y a x b x c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+． 5. 关于点()m n ，对称()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+- 根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．十、二次函数与一元二次方程：1. 二次函数与一元二次方程的关系（二次函数与x 轴交点情况）：一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数：① 当240b ac ∆=->时，图象与x 轴交于两点()()1200A x B x ，，，12()x x ≠，其中的12x x ，是一元二次方程()200ax bx c a ++=≠的两根．这两点间的距离21AB x x =-.② 当0∆=时，图象与x 轴只有一个交点； ③ 当0∆<时，图象与x 轴没有交点.1' 当0a >时，图象落在x 轴的上方，无论x 为任何实数，都有0y >； 2'当0a <时，图象落在x 轴的下方，无论x 为任何实数，都有0y <． 2. 抛物线2y ax bx c =++的图象与y 轴一定相交，交点坐标为(0，)c ；3. 二次函数常用解题方法总结：⑴ 求二次函数的图象与x 轴的交点坐标，需转化为一元二次方程；⑵ 求二次函数的最大（小）值需要利用配方法将二次函数由一般式转化为顶点式；⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ，b ，c 的符号，或由二次函数中a ，b ，c 的符号判断图象的位置，要数形结合；⑷ 二次函数的图象关于对称轴对称，可利用这一性质，求和已知一点对称的点坐标，或已知与x 轴的一个交点坐标，可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式，二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数；下面以0a >时为例，揭示二次函数、二次三项式和一元二次方程之间的内在联系：二次函数图像参考：十一、函数的应用二次函数应用⎧⎪⎨⎪⎩刹车距离何时获得最大利润最大面积是多少2-32y=-2x 2y=3(x+4)22y=3x 2y=-2(x-3)2二次函数考查重点与常见题型1． 考查二次函数的定义、性质，有关试题常出现在选择题中，如：已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点， 则m 的值是2． 综合考查正比例、反比例、一次函数、二次函数的图像，习题的特点是在同一直角坐标系内考查两个函数的图像，试题类型为选择题，如： 如图，如果函数b kx y +=的图像在第一、二、三象限内，那么函数12-+=bx kx y 的图像大致是（ ）3． 考查用待定系数法求二次函数的解析式，有关习题出现的频率很高，习题类型有中档解答题和选拔性的综合题，如： 已知一条抛物线经过(0,3)，(4,6)两点，对称轴为35=x ，求这条抛物线的解析式。