当前位置：文档之家 › 2017_2018八年级数学上册第13章轴对称13.3等腰三角形第1课时等腰三角形的性质习题课件

2017_2018八年级数学上册第13章轴对称13.3等腰三角形第1课时等腰三角形的性质习题课件

  • 格式：ppt
  • 大小：3.12 MB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

八年级数学上册 第13章 全等三角形 13.3 等腰三角形 13.3.2 等腰三角形的判定教案2 华

八年级数学上册 第13章 全等三角形 13.3 等腰三角形 13.3.2 等腰三角形的判定教案2 华
1.等腰三角形的判定方法？
2.等边三角形的判定方法？
二.导入课题，研究知识：
本节课我们来运用等腰三角形的判定方法来解决几个问题。
面向全体学生提出相关的问题。明确要研究，探索的问题是什么，怎样去研究和讨论。.
留给学生一定的思考和回顾知识的时间。
为学生创设表现才华的平台。
三.归纳知识，培养能力：
1.等腰三角形的判定方法？
2.等边三角形的判定方法？
四.运用知识，分析解题：例4 如图，AB∥CD,∠源自=∠2，求证：AB=AC.
例5 如图，在Rt△ABC和Rt△A′B′C′中，
∠ACB=∠A′B′C′=90°，AB= A′B′,AC=A′C′
求证：Rt△ABC≌Rt△A′B′C′.
五.课堂练习：请见教材
六.课后小结：等腰三角形的判定的应用.
七.课后作业：复印给学生
分析研究问题
将知识和实际问题相结合.
教学反思
等腰三角形的判定
教学目标
知识与技能
通过对问题的解答，学生能够进一步理解和掌握等腰三角形的判定方法.
过程与方法
提出问题，弄清题意，引导分析，运用知识，解决问题，提高能力.
情感态度与价值观
平移学生良好的学习品质.
教学重点
等腰三角形的判定方法.
教学难点
灵活运用解答问题.
教学内容与过程
教法学法设计
一.复习提问，回顾知识，请看下面的问题：

人教版八年级数学上册第13章2等边三角形

人教版八年级数学上册第13章2等边三角形

知2－练
4-1. 如图， 四边形ABCD 中，AB ∥ DC，DB 平分∠ ADC， ∠ A=60 °．求证：△ ABD 是等边三角形.
知2－练
证明：∵AB∥DC，∠A＝60°，∴∠ADC＝120°. ∵DB 平分∠ADC，∴∠ADB＝12∠ADC＝60°. ∴∠ABD＝180°－∠ADB－∠A＝60°. ∴∠A＝∠ADB＝∠ABD.∴△ADB 是等边三角形．
∴∠ CDE= ∠ ACB－∠ E=3 0 °.
∴∠ CDE= ∠ E.∴ CE=CD= 32.
2-1. 如图，△ ABC 为等边三角形， AD⊥BC，AE=AD，则∠ ADE= ___7_5_°__.
2-2. 如图，△ ABC 是等边三角形，BD 平分 ∠ ABC，点E 在BC 的延长线上，且 CE=1，∠ E=30°，则BC=______2__ .
3. 证明等边三角形的思维导图(如图13 .3 -29)
知2－讲
特别解读
知2－讲
1.在等腰三角形中，只要有一个角是60 °，无论
这个角是顶角还是底角，判定定理2 都成立.
2.等边三角形的判定方法：
(1)若已知三边关系，一般选用定义判定；
(2)若已知三角关系，一般选用判定定理1判定；
(3)若已知该三角形是等腰三角形，一般选用判定
∴ BC= 12AB.
知3－讲
2. 作用：应用于证线段的倍分关系和计算角度. 拓展：该性质反过来说也成立. 在直角三角形中，
如果一条直角边等于斜边的一半，那么它所对的角等 于30 °.
特别解读 应用此性质，必须满足两个条件： 1.在直角三角形中； 2.有一个锐角为30°.二者缺一不可.
知3－讲
知3－练
例6 如图13.3-33，在Rt △ ABC 中 ，∠ C=90° ，AB 边的垂 直平分线MN 交AB 于点M，交BC 于点N，且∠B=15° ， AC=4 cm，求BN 的长. 解题秘方：先构造含30 °角的 直角三角形，再利用含30 °角 的直角三角形的性质求线段长.

华东师大版八年级上册数学第13章13.3课题2 等腰三角形的判定

华东师大版八年级上册数学第13章13.3课题2 等腰三角形的判定

变例 已知△ABC中，∠BAC＝90°，AB＝AD＝AC， AD与BC相交于E，∠CAD＝30°. (1)求证：△ABD为等边三角形； (2)求∠DCB的度数． 解：(1)∵∠BAC＝90°，∠CAD＝30°. ∴∠BAD＝60°. 又∵AB＝AD. ∴△ABD为等边三角形(有一个角是60° 的等腰三角形是等边三角形)．
知识模块二 运用等腰三角形的判定进行证明和计算
范例 如图，在△ABC中，∠CBA＝90°，D是AB延长 线上一点，E在BC上，连结DE并延长交AC于点F，且 EF＝FC.求证：AF＝DF. 证明：∵EF＝FC，∴∠FEC＝∠C. ∵∠CBA＝90°. ∴∠A＋∠C＝90°，∠D＋∠BED＝90°. 又∵∠BED＝∠FEC，∴∠BED＝∠C. ∴∠A＝∠D. ∴AF＝DF.
(2)∵AD＝AC，∠CAD＝30°， ∴∠ADC＝∠ACD＝75°. 又△ABC中，∠BAC＝90°，AB＝AC， ∴∠ACB＝45°. ∴∠DCB＝75°－45°＝30°.
第13章 全等三角形 13.3 等腰三角形
课题2 等腰三角形的判定
学习目标
1．掌握等腰三角形的判定定理，会用等腰三角形的判 定进行简单的推理、判断及应用； 2．通过猜想的提出、定理与推论的证明、实际问题的 解决及问题的变式引用； 3．结合等腰三角形性质的探索与证明过程，体会轴对 称在研究几何问题中的作用． 【习重点】 等腰三角形的性质． 【学习难点】 等腰三角形判定与性质的区别．
情景导入
回顾：1.怎样的三角形叫等腰三角形？ 有两条边相等的三角形叫等腰三角形． 2．在△ABC中，AB＝AC，AD是角平分线，且BD＝ 10cm，则BC＝_2_0_cm. 3．在△ABC中，BC＝AC，∠A＝55°，∠C＝_7_0_°．

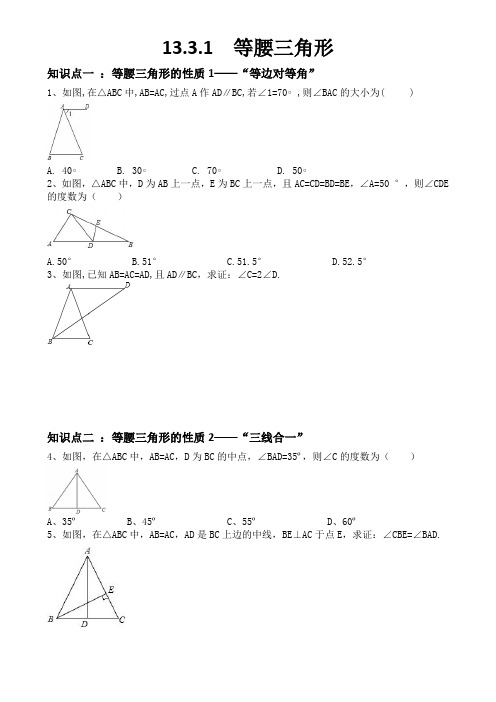
人教版八年级上第13章 13.3 .1等腰三角形

人教版八年级上第13章 13.3 .1等腰三角形

13.3.1 等腰三角形知识点一：等腰三角形的性质1——“等边对等角”1、如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70∘,则∠BAC的大小为( )A. 40∘B. 30∘C. 70∘D. 50∘2、如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50 °，则∠CDE 的度数为（）A.50°B.51°C.51.5°D.52.5°3、如图,已知AB=AC=AD,且AD∥BC，求证：∠C=2∠D.知识点二：等腰三角形的性质2——“三线合一”4、如图，在△ABC中，AB=AC，D为BC的中点，∠BAD=35º，则∠C的度数为（）A、35ºB、45ºC、55ºD、60º5、如图，在△ABC中，AB=AC，AD是BC上边的中线，BE⊥AC于点E，求证：∠CBE=∠BAD.知识点三：等腰三角形的判定6、如图,在△ABC中,∠ABC=60∘,∠C=45∘,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形( )A. 2个B. 3个C. 4个D. 5个7、如图，在△ABC中，AD⊥BC于D，点M、N分别在BC所在的直线上，且AB=AC，BM=CN，试判断△AMN的形状，并说明理由。

综合练习题：一、填空题。

1、如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114∘,则∠DFC为( )A. 114∘B. 123∘C. 132∘D. 147∘2、等腰三角形一腰上的高与底边所夹的角（）A. 等于顶角B. 等于顶角的一半C. 等于顶角的2倍D. 等于底角的一半3、平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )A. 5B. 6C. 7D. 84、如图,在△ABC中,AB=AC,AD⊥BC于点D,则下列结论不一定成立的是( )A. AD=BDB. BD=CDC. ∠1=∠2D. ∠B=∠C5、在△ABC中,下列哪个点与△ABC的任意两个顶点,围成的三角形都是等腰三角形( )A. 三条中线的交点B. 三条高线的交点C. 三条角平分线的交点D. 三条垂直平分线的交点6、等腰三角形有一个角是90º，则另两个角分别是（）A. 30º，60ºB. 45º，45ºC. 45º，90ºD. 20º，70º7、如图,在△ABC中,BD平分∠ABC,ED∥BC,已知AB=3,AD=1,则△AED的周长为 ( )A. 2B. 3C. 4D. 58、如图，在△ABC中，∠A=36º，AB=AC，BD是△ABC的角平分线，若在边AB上截取BE=BC，连接DE，则图中等腰三角形共有（）A. 2个B. 3个C. 4个D. 5个9、已知△ABC中,AB=6,AC=8,BC=11,任作一条直线将△ABC分成两个三角形,若其中有一个三角形是等腰三角形,则这样的直线最多有( )A. 3条B. 5条C. 7条D. 8条二、填空题1、等腰三角形的一个内角为70∘，它一腰上的高与底边所夹的度数为___.2、如图,BD,CE分别是△ABC两个外角的角平分线,DE过点A,且DE∥BC.若DE=14，BC=7，则△ABC的周长为___.3、如图,∠BOC=60∘,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s 的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间，当t=___s时，△POQ是等腰三角形。

等腰三角形的性质

等腰三角形的性质

满足三角形任意两边之和大于第三边，
∴这个等腰三角形另两条边长分别为19 cm，19 cm. B
C
D
➢ 解决这个问题的关键是等腰三角形的腰相等， 那么两个底角也相等吗？
获取新知
剪一张等腰三角形的半透明纸片，每人所剪的等腰三角形的大小和 形状可以不一样，如图，把纸片对折，让两腰AB、AC重叠在一起， 折痕为AD.你能发现什么现象吗？
等腰三角形的两底角相等的定理证明：
已知: 如图 ,在 △ABC中，AB＝AC.
求证： ∠B＝∠C.
证明：画∠ABC的平分线AD.
在 △ABD和 △ACD中，
A
∵ AB＝AC (已知），
12
∠1 =∠2(角平分线的定义），
提示：要证明∠B＝∠C ,可 设法构造两个全等三角 ， 使∠B、∠C分别是这两个 全等三角形的对应角，于是 想到画∠BAC的平分线AD.
②∵AB＝AC，BD＝DC，
∴AD⊥BC(或AD平分∠BAC)；
③∵AB＝AC，AD平分∠BAC，
∴BD＝DC(或AD⊥BC)．
根据等腰三角形性质完成下列填空.
在△ABC中， AB=AC时，
（1）∵AD是底边上的高，
A
∴∠_1__ = ∠_2__，_B_D__= _C_D__.
12
(2) ∵AD是中线，
当底边长为12 cm时，设腰长为ycm， 由题意得： 2y＋12＝50， ∴y＝19.
你能画出这两种结果的三角形吗？
➢当腰长为12 cm时，
∵12＋12＝24＜26，∴不满足三角形任意两边之和大于第三边．
这样的三角形不存在，画不出来。
A
➢ 当底边长为12 cm时，三角形三条边长分别为12 cm，

八年级数学人教版上册第13章轴对称图形13.3.2等边三角形(图文详解)

八年级数学人教版上册第13章轴对称图形13.3.2等边三角形(图文详解)

八年级数学上册第13章轴对称
通过本课时的学习，需要我们掌握： 一.等边三角形的判定 1.三条边都相等的三角形是等边三角形. 2. 三个角都相等的三角形是等边三角形. 3.有一个角是60°的等腰三角形是等边三角形. 二.定理： 如果在直角三角形中，如果一个锐角等于30°， 那么，它所对的直角边等于斜边的一半.
八年级数学上册第13章轴对称
A
想想看，等边三角形 有什么性质？
B
C
⑴三边之间 AB＿＝AC＿＝BC
⑵三角之间∠A＿＝∠B＿＝∠C
八年级数学上册第13章轴对称
等边三角形的性质 A
B ）60°
60（° C
⑴等边三角形的三边都相等；
⑵等边三角形的三个内角都相等,并且每一个角都等于 60°.
八年级数学上册第13章轴对称
八年级数学上册第13章轴对称
1.如图,∠Ｃ＝90°，Ｄ是ＣＡ的延长线上一点,
1
∠ＢＤＣ＝15°，且ＡＤ＝ＡＢ，则ＢＣ=_____2 AD.
Ｂ
Ｃ
Ａ
Ｄ
八年级数学上册第13章轴对称
2.（2010·宿迁中考）数学活动课上，老师在黑板上画直 线l平行于射线AN（如图），让同学们在直线和射线上各找 一点B和C，使得以A、B、C为顶点的三角形是等腰直角三角 形．这样的三角形最多能画______个．
【解析】分别以A 、B、 C为直角顶点,则共有3个等腰直角 三角形. 答案：3
八年级数学上册第13章轴对称
3.（2010·聊城中考）如图，在等边△ABC中，点D是BC边 的中点，以AD为边作等边△ADE，求∠CAE的度数.
A
F E
B
D
C
【解析】点D是等边△ABC中BC边的中点，故∠DAC＝ 30°;在等边△ADE中， ∠CAE=60°-30°=30°. 答：∠CAE=30°.

南华县第一中学八年级数学上册第十三章轴对称13.3等腰三角形1等腰三角形第1课时等腰三角形的性质教学


结束语
同学们，你们要相信梦想是价值的源泉，相信成 功的信念比成功本身更重要，相信人生有挫折没 有失败，相信生命的质量来自决不妥协的信念，
考试加油!奥利给~
第十一章 三角形
章末复习 (一) 三角形
知识点一 三角形的三边关系
1．(2019·台州)以下长度的三条线段 , 能组成三角形的是(B
)
A．3 , 4 , 8
A．∠A＋∠B＝∠C B．∠A－∠B＝∠C C．∠A∶∠B∶∠C＝1∶2∶3 D．∠A＝∠B＝3∠C
12．如果在△ABC中 , ∠A＝60°＋∠B＋∠C , 那么∠A等于( ) C
A．30° B．60° C．120° D．140°
13．一张△ABC纸片 , 点M , N分别是AB , AC上的点 , 假设沿直线MN折叠
第十三章 轴対称
等腰三角形〔1〕
【学习目标] 1、了解等腰三角形的概念 , 掌握等腰
三角形的性质 ; 2、运用等腰三角形的概念及性质解决
相关问题。 【学习重、难点] 重难点 : 等腰三角形的性质及其应用。
【预习导学]
（一）自学指导
1、自学1 : 自学课本P2页 , 〞探究、思考与例1” , 掌握等
等边対等角
总结归纳 : ①等腰三角形的两个
相等
B
A
D
C
〔中简线写成〞
高 ”〕
②等腰三角形的顶角的平対分称线轴 , 底边上
的
、底边上的 互相重合 ;
③等腰三角形是轴対称图形 ,
是
底边上的中线〔顶角平分线、底边上的高〕所在的直线。
【预习导学]
（二）自学检测 : 学生自主完成 , 小组内展示、点评 , 教师巡视。
A．只有①准确

2017-2018学年八年级数学上册 第十三章 轴对称 微专题 构造等腰三角形技巧(三)折半加倍

微专题构造等腰三角形技巧(三)折半加倍法【方法技巧】在已知条件中出现二倍角关系时，可作二倍角的平分线构造等腰三角形，或延长二倍角的一边，使其等于二倍角的另一边，构造两个等腰三角形，将倍角关系转化为等角关系．基本图形：△ABC中，∠ABC＝2∠C，①如图1，作∠ABC的平分线交AC于D，则可构造等腰△DBC.②如图2，延长CB到D，使BD＝AB，则可构造等腰△ABD和等腰△ACD.一、作二倍角的平分线构造等腰三角形1．如图，△ABC中，∠ACB＝2∠B，求证：2AC＞AB.【解题过程】证明：延长BC至D，使CD＝AC，则AB＝AD，∵AC＋CD＞AD，∴2AC＞AB.2．如图，△ABC中，∠ACB＝2∠A，AC＝2BC，求证：∠B＝90°(2种方法)．(导学号：58024183)图1 图2【解题过程】证明：方法一：如图1，作∠ACB的平分线交AB于D，过D作DE⊥AC于E，证CD＝AD，AE＝CE＝BC，△BCD≌△ECD即可；方法二：如图2，作∠ACB的平分线交AB于D，延长CB至E，使CE＝AC，先证△ACD≌△ECD，再证CD＝DE，BC＝BE，∴DB⊥CE.二、延长二倍角的一边构造等腰三角形3．如图，在△ABC中，∠BAC＝2∠B，CD平分∠ACB交AB于点D，求证：AC＋AD＝BC(3种方法)．(导学号：58024184)图1 图2 图3 【解题过程】证明：方法一：如图1，延长CA 至E ，使EA ＝AD ，证△CDE ≌△CDB 即可； 方法二：如图2，延长DA 至E ，使EA ＝AC ，证ED ＝EC ＝BC 即可； 方法三：如图3，在BC 上截取CE ＝AC ，证AD ＝DE ＝BE 即可．【点评】方法一、方法二实质是补短法，方法三实质是截长法．。

2022年秋八年级数学上册 第13章 轴对称 13.3 等腰三角形 13.3.1 等腰三角形 第1课


•
12、人乱于心，不宽余请。2022/3/12022/3/12022/3/1Tuesday, March 01, 2022
•
13、生气是拿别人做错的事来惩罚自 己。2022/3/12022/3/12022/3/12022/3/13/1/2022
•
14、抱最大的希望，作最大的努力。2022年3月1日 星期二2022/3/12022/3/12022/3/1
A．80°
B．80°或 20°
C．80°或 50°
D．20°
1．如图，AB＝AC，△ABC 的外角∠DAC＝100°，则∠B 的度数为( D )
A．80° C．60°
B．70° D．50°
2．如图在等腰△ABC 中，AB＝AC，BD⊥AC，∠ABC＝72°，则∠ABD 等 于( B )
A．36° C．18°
•

15、一个人炫耀什么，说明他内心缺 少什么 。。2022年3月 2022/3/12022/3/12022/3/13/1/2022
•
16、业余生活要有意义，不要越轨。2022/3/12022/3/1Marc h 1, 2022
等腰三角形的三线合一
等腰三角形的顶角平分线 、底边上的中线、 底边上的高线 相互重合(简写
成“三线合一”)．
自我诊断 2. 如图，AB＝AC，D 是 BC 的中点，下列结论不正确的是( D )
A．∠B＝∠C
B．AD⊥BC
C．AD 平分∠BAC
D．AB＝2BD
易错点：在求等腰三角形的角时易漏解．
自我诊断 3. 等腰三角形的一个角是 80°，则它的顶角的度数是( B )
14．如图，已知点 E 为等腰△ABC 的底边 BC 上一动点，过点 E 作 EF⊥ BC 交 AB 于点 D，交 CA 的延长线于点 F，问： (1)∠F 与∠ADF 的关系怎样？说明理由； (2)若 E 在 BC 延长线上，其余条件不变，上题的结论是否成立？若不成立， 说明理由；若成立，画出图形并给予证明．

13.3等腰三角形


D．65 °
【详解】 ∵三角形为等腰三角形，且顶角为50°， ∴底角=（180°-50°）÷2=65°． 故选：D．
课堂测试
5、如果一个等腰三角形的两边长为4、9，则它的周长为( )
A．17
B．22
C．17或22 D．无法计算
【分析】 求等腰三角形的周长，即是确定等腰三角形的腰与底的长求周长；题目给出等腰三角形有两条边长为 4和9，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成 三角形． 【详解】 解：（1）若4为腰长，9为底边长， 由于4+4＜9，则三角形不存在； （2）若9为腰长，则符合三角形的两边之和大于第三边． 所以这个三角形的周长为9+9+4=22． 故选：B．
小结
满足什么条件的三角形是等腰三角形? 方法1:有两边相等的三角形是等腰三角形.(定义)
方法2:有两个角相等的三角形是等腰三角形.(定理)
结合边和角来看,会有什 么新的结论吗?
满足什么条件的三角形是等边三角形
三条边都相等的三角形 是等边三角形(定义)
三个角都相等的三角形 是等边三角形
有一个角是60°的等腰 三角形是等边三角形
2、等腰三角形的性质： ①等腰三角形的两个底角相等,（简写成“ 等边对等角 ”） ②等腰三角形顶角的平分线、底边上的中线和底边上的高互相重 合。（简称“ 三线合一 ”） ③等腰三角形是 轴对称 图形。
思考
我们知道，如果一个三角形有两条边相等，那么他们所对的角相等。反过来，如果一 个三角形有两个角相等，那么它们所对的边有什么关系？
第13章 轴对称
13.3.1-1等腰三角形性质
前言
学习目标
1、经历操作、发现、猜想、证明的过程，探索等腰三角形的性质，感受数学思考过程的条理性， 培养学生的逻辑思维能力. 2、初步学会从数学的角度发现问题和提出问题，综合运用已有的知识解决新的问题.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。