三角函数综合_知识讲解_基础

中考总复习：锐角三角函数综合复习—知识讲解（基础）【考纲要求】1.理解锐角三角函数的定义、性质及应用，特殊角三角函数值的求法，运用锐角三角函数解决与直角三角形有关的实际问题.题型有选择题、填空题、解答题，多以中、低档题出现；2.命题的热点为根据题中给出的信息构建图形，建立数学模型，然后用解直角三角形的知识解决问题. 【知识网络】【考点梳理】考点一、锐角三角函数的概念如图所示，在Rt △ABC 中，∠C ＝90°，∠A 所对的边BC 记为a ，叫做∠A 的对边，也叫做∠B 的邻边，∠B 所对的边AC 记为b ，叫做∠B 的对边，也是∠A 的邻边，直角C 所对的边AB 记为c ，叫做斜边．BCabc锐角A 的对边与斜边的比叫做∠A 的正弦，记作sinA ，即sin A aA c ∠==的对边斜边；锐角A 的邻边与斜边的比叫做∠A 的余弦，记作cosA ，即cos A bA c ∠==的邻边斜边；锐角A 的对边与邻边的比叫做∠A 的正切，记作tanA ，即tan A aA A b∠==∠的对边的邻边.同理sin B b B c ∠==的对边斜边；cos B aB c∠==的邻边斜边；tan B b B B a ∠==∠的对边的邻边．要点诠释：(1)正弦、余弦、正切函数是在直角三角形中定义的，反映了直角三角形边与角的关系，是两条线段的比值．角的度数确定时，其比值不变，角的度数变化时，比值也随之变化．(2)sinA，cosA，tanA分别是一个完整的数学符号，是一个整体，不能写成，，，不能理解成sin与∠A，cos与∠A，tan与∠A的乘积．书写时习惯上省略∠A的角的记号“∠”，但对三个大写字母表示成的角(如∠AEF)，其正切应写成“tan∠AEF”，不能写成“tanAEF”；另外，、、常写成、、．(3)任何一个锐角都有相应的锐角三角函数值，不因这个角不在某个三角形中而不存在．(4)由锐角三角函数的定义知：当角度在0°＜∠A＜90°之间变化时，，，tanA＞0．考点二、特殊角的三角函数值利用三角函数的定义，可求出30°、45°、60°角的各三角函数值，归纳如下：锐角30°45° 160°要点诠释：(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．(2)仔细研究表中数值的规律会发现：、、的值依次为、、，而、、的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：当角度在0°＜∠A＜90°之间变化时，①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)，②余弦值随锐角度数的增大(或减小)而减小(或增大)．考点三、锐角三角函数之间的关系如图所示，在Rt△ABC中，∠C=90°．(1)互余关系：，；(2)平方关系：；(3)倒数关系：或；(4)商数关系：．要点诠释：锐角三角函数之间的关系式可由锐角三角函数的意义推导得出，常应用在三角函数的计算中，计算时巧用这些关系式可使运算简便．考点四、解直角三角形在直角三角形中，由已知元素(直角除外)求未知元素的过程，叫做解直角三角形.在直角三角形中，除直角外，一共有5个元素，即三条边和两个锐角.设在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，则有：①三边之间的关系：a2+b2=c2(勾股定理).②锐角之间的关系：∠A+∠B=90°.③边角之间的关系：，，，，，.④，h为斜边上的高.要点诠释：(1)直角三角形中有一个元素为定值(直角为90°)，是已知的值.(2)这里讲的直角三角形的边角关系指的是等式，没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形，可以更加清楚、直观地理解.考点五、解直角三角形的常见类型及解法已知条件解法步骤Rt△ABC 两边两直角边(a，b)由求∠A，∠B=90°－∠A，斜边，一直角边(如c，a) 由求∠A，∠B=90°－∠A，一边一角一直角边和一锐角锐角、邻边(如∠A，b)∠B=90°－∠A，，锐角、对边(如∠A，a)∠B=90°－∠A，，斜边、锐角(如c，∠A)∠B=90°－∠A，，要点诠释：1．在遇到解直角三角形的实际问题时，最好是先画出一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的，然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2．若题中无特殊说明，“解直角三角形”即要求出所有的未知元素，已知条件中至少有一个条件为边.考点六、解直角三角形的应用解直角三角形的知识应用很广泛，关键是把实际问题转化为数学模型，善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是：(1)弄清题中名词、术语的意义，如仰角、俯角、坡度、坡角、方向角等概念，然后根据题意画出几何图形，建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义，得出实际问题的解.拓展：在用直角三角形知识解决实际问题时，经常会用到以下概念：(1)坡角：坡面与水平面的夹角叫做坡角，用字母表示.坡度(坡比)：坡面的铅直高度h和水平距离的比叫做坡度，用字母表示，则，如图，坡度通常写成=∶的形式.(2)仰角、俯角：视线与水平线所成的角中，视线中水平线上方的叫做仰角，在水平线下方的叫做俯角，如图.(3)方位角：从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角，如图①中，目标方向PA，PB，PC的方位角分别为是40°，135°，245°.(4)方向角：指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角，如图②中的目标方向线OA，OB，OC，OD的方向角分别表示北偏东30°，南偏东45°，南偏西80°，北偏西60°.特别如：东南方向指的是南偏东45°，东北方向指的是北偏东45°，西南方向指的是南偏西45°，西北方向指的是北偏西45°.要点诠释：1．解直角三角形实际是用三角知识，通过数值计算，去求出图形中的某些边的长或角的大小，最好画出它的示意图.2．非直接解直角三角形的问题，要观察图形特点，恰当引辅助线，使其转化为直角三角形或矩形来解.例如：3．解直角三角形的应用题时，首先弄清题意(关键弄清其中名词术语的意义)，然后正确画出示意图，进而根据条件选择合适的方法求解.【典型例题】类型一、锐角三角函数的概念与性质1．如图，在4×4的正方形网格中，tanα=( )(A)1 (B)2 (C) 12(D)52【思路点拨】把∠α放在一个直角三角形中，根据网格的长度计算出∠α的对边和邻边的长度.【答案】B；【解析】根据网格的特点：设每一小正方形的边长为1，可以确定∠α的对边为2，邻边为1，然后利用正切的定义tan∠αα=∠α的对边的邻边，故选B.【总结升华】本题考查锐角三角函数的定义及运用，可将其转化到直角三角形中解答，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．举一反三：【变式】在Rt△ABC中，∠C=90°,若AC=2BC，则sinA的值是( )(A) 12(B)2 (C)55(D)52【答案】选C.因为∠C=90°，522AB=AC +BC =BC ，所以BC BC 5sin A AB 55BC===.类型二、特殊角的三角函数值2．已知a ＝3，且21(4tan 45)302b bc -++-=°，以a 、b 、c 为边长组成的三角形面积等于( )． A ．6 B ．7 C ．8 D ．9【思路点拨】根据题意知4tan 450,130,2b bc -=⎧⎪⎨+-=⎪⎩°求出b 、c 的值，再求三角形面积. 【答案】A ；【解析】根据题意知4tan 450,130,2b bc -=⎧⎪⎨+-=⎪⎩° 解得 4,5.b c =⎧⎨=⎩ 所以a ＝3，b ＝4，c ＝5，即222a b c +=，其构成的三角形为直角三角形，且∠C ＝90°， 所以162S ab ==． 【总结升华】利用非负数之和等于0的性质，求出b 、c 的值，再利用勾股定理的逆定理判断三角形是直角三角形，注意tan45°的值不要记错． 举一反三： 【变式】 计算：.【答案】原式.3．如图所示，在△ABC 中，∠BAC ＝120°，AB ＝10，AC ＝5，求sinB ·sinC 的值．【思路点拨】为求sin B ，sin C ，需将∠B ，∠C 分别置于直角三角形之中，另外已知∠A 的邻补角是60°，若要使其充分发挥作用，也需要将其置于直角三角形中，所以应分别过点B 、C 向CA 、BA 的延长线作垂线，即可顺利求解． 【答案与解析】解：过点B 作BD ⊥CA 的延长线于点D ，过点C 作CE ⊥BA 的延长线于点E ．∵∠BAC ＝120°，∴∠BAD ＝60°．∴AD ＝AB ·cos60°＝10×12＝5； BD ＝AB ·sin60°＝10×32＝53． 又∵CD ＝CA+AD ＝10， ∴2257BC BD CD =+=，∴21sin 7BD BCD BC ∠==． 同理，可求得21sin 14ABC ∠=． ∴21213sin sin 71414ABC BCD ∠∠=⨯=． 【总结升华】由于锐角的三角函数是在直角三角形中定义的，因此若要求某个角的三角函数值，一般可以通过作垂线等方法将其置于直角三角形中．举一反三：【变式】如图，机器人从A 点，沿着西南方向，行了个单位，到达B 点后观察到原点O 在它的南偏东60°的方向上，则原来A 的坐标为__________.(结果保留根号)．【答案】类型三、解直角三角形及应用4．在△ABC中，∠A＝30°，BC＝3，AB＝33，求∠BCA的度数和AC的长．【思路点拨】由于∠A是一个特殊角，且已知AB，故可以作AC边上的高BD(如图所示)，可求得332BD=．由于此题的条件是“两边一对角”，且已知角的对边小于邻边，因此需要判断此题的解是否唯一，要考虑对边BC与AC边上的高BD的大小，而33332BC<<，所以此题有两解．【答案与解析】解：作BD⊥AC于D．(1)C1点在AD的延长线上．在△ABC1中，13BC=，332 BD=，∴13sin2C=．∴∠C1＝60°．由勾股定理，可分别求得13 2DC=，92 AD=．∴AC1＝AD+DC1＝936 22+=．(2)C2点在AD上．由对称性可得，∠BC2D＝∠C1＝60°，213 2C D C D==．∴∠BC2A＝120°，2933 22AC=-=．综上所述，当∠BCA＝60°时，AC＝6；当∠BCA＝120°时，AC＝3．【总结升华】由条件“两边一对角”确定的三角形可能不是唯一的，需要考虑第三边上的高的大小判断解是否唯一．5．（2015•茂名）如图，一条输电线路从A地到B地需要经过C地，图中AC=20千米，∠CAB=30°，∠CBA=45°，因线路整改需要，将从A地到B地之间铺设一条笔直的输电线路．（1）求新铺设的输电线路AB的长度；（结果保留根号）（2）问整改后从A地到B地的输电线路比原来缩短了多少千米？（结果保留根号）【思路点拨】（1）过C作CD⊥AB，交AB于点D，在直角三角形ACD中，利用锐角三角函数定义求出CD与AD的长，在直角三角形BCD中，利用锐角三角函数定义求出BD的长，由AD+DB求出AB的长即可；（2）在直角三角形BCD中，利用勾股定理求出BC的长，由AC+CB﹣AB即可求出输电线路比原来缩短的千米数．【答案与解析】解：（1）过C作CD⊥AB，交AB于点D，在Rt△ACD中，CD=AC•sin∠CAD=20×=10（千米），AD=AC•cos∠CAD=20×=10（千米），在Rt△BCD中，BD===10（千米），∴AB=AD+DB=10+10=10（+1）（千米），则新铺设的输电线路AB的长度10（+1）（千米）；（2）在Rt△BCD中，根据勾股定理得：BC==10（千米），∴AC+CB﹣AB=20+10﹣（10+10）=10（1+﹣）（千米），则整改后从A地到B地的输电线路比原来缩短了10（1+﹣）千米．【总结升华】解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．已知斜三角形中的SSS，SAS，ASA，AAS以及SSA条件，求三角形中的其他元素是常见问题，注意划归为常见的两个基本图形(高在三角形内或高在三角形外)(如图所示)：举一反三：【变式】坐落在山东省汶上县宝相寺内的太子灵踪塔始建于北宋(公元1112年)，为砖砌八角形十三层楼阁式建筑．数学活动小组开展课外实践活动，他们去测量太子灵踪塔的高度，携带的测量工具有：测角仪、皮尺、小镜子．(1)小华利用测角仪和皮尺测量塔高．下图为小华测量塔高的示意图．她先在塔前的平地上选择一点A，用测角仪测出看塔顶(M)的仰角α＝35°，在点A和塔之间选择一点B，测出看塔顶(M)的仰角β＝45°，然后用皮尺量出A ，B 两点间的距离为18.6m ，量出自身的高度为1.6m ．请你利用上述数据帮助小华计算出塔的高度(tan35°≈0.7，结果保留整数)．(2)如果你是活动小组的一员，正准备测量塔高，而此时塔影NP 的长为am(如图所示)，你能否利用这一数据设计一个测量方案?如果能，请回答下列问题：①在你设计的测量方案中，选用的测量工具是：________________________；②要计算出塔的高，你还需要测量哪些数据?________________________________________________________. 【答案】解：(1)设CD 的延长线交MN 于E 点，MN 长为x m ，则ME ＝(x-1.6)m ． ∵β＝45°，∴DE ＝ME ＝x-1.6．∴CE ＝x-1.6+18.6＝x+17．∵tan tan 35MECE α==°， ∴ 1.60.717x x -=+，解得x ＝45．∴太子灵踪塔MN 的高度为45m ．(2)①测角仪、皮尺；②站在P 点看塔顶的仰角、自身的高度(注：答案不唯一)．6．如图，三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航，某一时刻航行到A处，测得该岛在北偏东30°方向，海监船以20海里/时的速度继续航行，2小时后到达B处，测得该岛在北偏东75°方向，求此时海监船与黄岩岛P的距离BP的长．（参考数据：≈1.414，结果精确到0.1）【思路点拨】过B作BD⊥AP于D，由已知条件得：AB=20×2=40，∠P=75°﹣30°=45°，在Rt△ABD中求出BD=AB=20，在R t△BDP中求出PB即可．【答案与解析】解：过B作BD⊥AP于D，由已知条件得：AB=20×2=40，∠P=75°﹣30°=45°，在Rt△ABD中，∵AB=40，∠A=30，∴BD=AB=20，在R t△BDP中，∵∠P=45°，∴PB=BD=20≈28.3（海里）．答：此时海监船与黄岩岛P的距离BP的长约为28.3海里．【总结升华】此题主要考查解直角三角形的有关知识．通过数学建模把实际问题转化为解直角三角形问题．中考总复习：锐角三角函数综合复习—巩固练习（基础）【巩固练习】一、选择题1. 如图所示，在Rt △ABC 中，∠ACB ＝90°，BC ＝1，AB ＝2，则下列结论正确的是 ( ) A ．sin A ＝32 B ．tan A ＝12C ．cosB ＝32D ．tan B ＝3第1题 第2题2．如图，在Rt△ABC 中，∠ACB=90°，CD⊥AB，垂足为D ．若AC=5，BC=2，则sin∠ACD 的值为（ ）A ．53B ．255 C ．52D ．233．在△ABC 中，若三边BC 、CA 、AB 满足 BC ∶CA ∶AB=5∶12∶13，则cosB=（ ）A ．125B ．512 C ．135 D ．13124．如图所示，在△ABC 中，∠C=90°，AD 是BC 边上的中线，BD=4，AD=25，则tan ∠CAD 的值是（ ）A.2B.2C.3D.5第4题 第6题5．一个物体从A 点出发，沿坡度为1：7的斜坡向上直线运动到B ，AB=30米时，物体升高（ ）米． A ．B ．3C ．D ． 以上的答案都不对6．如图，已知：45°＜A ＜90°，则下列各式成立的是（ ）A.sinA=cosAB.sinA ＞cosAC.sinA ＞tanAD.sinA ＜cosA二、填空题7．若∠α的余角是30°，则cosα的值是 .8．如图，△ABC的顶点都在方格纸的格点上，则sinA=_______.第8题第12题9．计算2sin30°﹣sin245°+t an30°的结果是 .10．已知α是锐角，且sin(α+15°)=32.计算1184cos( 3.14)tan3απα-⎛⎫---++ ⎪⎝⎭的值为 .11．如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为海里．（结果保留根号）12．如图，正方体的棱长为3，点M，N分别在CD，HE上，CM=12DM，HN=2NE，HC与NM的延长线交于点P，则tan∠NPH的值为．三、解答题13．如图所示，我市某广场一灯柱AB被一钢缆CD固定，CD与地面成40°夹角，且DB＝5m，现要在C 点上方2m处加固另一条钢缆ED，那么EB的高为多少米?(结果保留三个有效数字)14. 已知：如图所示，八年级(1)班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC，他们首先在A点处测得建筑物CD的顶部D点的仰角为25°，然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′．已知建筑物AB的高度为30米，求两建筑物的水平距离AC(精确到0.1米)（可用计算器查角的三角函数值）15．如图，登山缆车从点A出发，途经点B后到达终点C，其中AB段与BC段的运行路程均为200m，且AB段的运行路线与水平面的夹角为30°，BC段的运行路线与水平面的夹角为42°，求缆车从点A运行到点C的垂直上升的距离．（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）16. 如图所示，某水库大坝的横断面是梯形，坝顶宽AD＝2.5m，坝高4 m，背水坡的坡度是1：1，迎水坡的坡度是1：1.5，求坝底宽BC.【答案与解析】一、选择题1.【答案】D ； 【解析】sinA ＝BC AB ＝12，tan A ＝BC AC ＝33，cosB ＝BC AB ＝12．故选D.2.【答案】A ；【解析】在直角△ABC 中，根据勾股定理可得：AB=2AC BC +2=2(5)2+2=3．∵∠B+∠BCD=90°，∠ACD+∠BCD=90°， ∴∠B=∠ACD． ∴ sin∠ACD=sin∠B=ACAB =53， 故选A ．3.【答案】C ；【解析】根据三角函数性质 cosB==，故选C ．4.【答案】A ；【解析】∵AD 是BC 边上的中线，BD=4，∴CD=BD=4，在Rt △ACD 中，AC= 22AD -CD =-=222（25）4，∴tan ∠CAD===2．故选A ．5.【答案】B ；【解析】∵坡度为1：7，∴设坡角是α，则sinα===，∴上升的高度是：30×=3米．故选B ．6.【答案】B ；【解析】∵45°＜A ＜90°，∴根据sin45°=cos45°，sinA 随角度的增大而增大，cosA 随角度的增大而减小， 当∠A ＞45°时，sinA ＞cosA ，故选B ．二、填空题 7．【答案】21； 【解析】∠α=90°﹣30°=60°，cosα=cos60°=21．8．【答案】；【解析】过C 作CD ⊥AB ，垂足为D ，设小方格的长度为1，在Rt △ACD 中，AC=22CD AD +=25,∴sinA=CD 5=AC 5.9．【答案】21+33； 【解析】2sin30°﹣sin 245°+ t an30°=2×21－（22）2+（）2+33=1﹣21+33=21+33．10．【答案】3； 【解析】∵sin60°=32，∴α+15°=60°，∴α=45°，∴原式=22﹣4×22﹣1+1+3=3． 11．【答案】40 ；【解析】解：作PC ⊥AB 于C ，在Rt △PAC 中，∵PA=80，∠PAC=30°，∴PC=40海里，在Rt △PBC 中，PC=40，∠PBC=∠BPC=45°， ∴PB=40海里，故答案为：40．12．【答案】13； 【解析】∵正方体的棱长为3，点M ，N 分别在CD ，HE 上，CM=12DM ，HN=2NE ， ∴MC=1，HN=2， ∵DC ∥EH ， ∴12PC MC PH NH ==， ∵HC=3， ∴PC=3， ∴PH=6， ∴tan ∠NPH=2163NH PH ==，故答案为：13．三、解答题13.【答案与解析】解：在Rt△BCD中，∠BDC＝40°，DB＝5 m，∵tanBC BDCDB ∠=．∴BC＝DB·tan∠BDC＝5×tan40°≈4.195(米)．∴EB＝BC+CE＝4.195+2≈6.20(米)．14.【答案与解析】解：如图所示，过D作DH⊥AB，垂足为H．设AC＝x．在Rt△ACD中，∠ACD＝90°，∠DAC＝25°，所以CD＝AC·tan∠DAC＝x tan 25°．在Rt△BDH中，∠BHD＝90°，∠BDH＝15°30′，所以BH＝DH·tan 15°30′＝AC·tan 15°30′＝x·tan 15°30′．又CD＝AH，AH+HB＝AB，所以x(tan 25°+tan 15°30′)＝30．所以3040.3tan25tan1530x='+≈°°(米)．答：两建筑物的水平距离AC约为40.3米．15.【答案与解析】解：在Rt△ADB中，∵∠ADB=90°，∠BAD=30°，AB=200m，∴BD=AB=100m，在Rt△CEB中，∵∠CEB=90°，∠CBE=42°，CB=200m，∴CE=BC•sin42°≈200×0.67=134m，∴BD+CE≈100+134=234m．答：缆车从点A运行到点C的垂直上升的距离约为234m．16.【答案与解析】解：背水坡是指AB，而迎水坡是指CD.过A作AE⊥BC于E，过D作DF⊥BC于F，由题意可知tanB＝1，tan C＝1 1.5，在Rt△ABE中，AE＝4，tanB＝AEBE＝1，∴BE＝AE＝4，在Rt△DFC中，DF＝AE＝4，tanC＝11.5 DFCF，∴CF＝1．5DF＝1.5×4＝6．又∵EF＝AD＝2.5，∴BC＝BE＋EF＋FC＝4＋2.5＋6＝12．5．答：坝底宽BC为12．5 m．。

三角函数知识点及题型归纳三角函数是数学中的一个重要分支，在几何、物理、工程等领域都有广泛的应用。

下面我们来详细归纳一下三角函数的知识点和常见题型。

一、三角函数的基本概念1、角的概念角可以分为正角、负角和零角。

按旋转方向，逆时针旋转形成的角为正角，顺时针旋转形成的角为负角，没有旋转的角为零角。

2、弧度制把长度等于半径长的弧所对的圆心角叫做 1 弧度的角。

用弧度作为单位来度量角的制度叫做弧度制。

弧度与角度的换算公式为：180°＝π 弧度。

3、任意角的三角函数设角α的终边上任意一点 P 的坐标为(x, y)，它与原点的距离为 r(r ＝√（x²＋ y²) ＞ 0)，则角α的正弦、余弦、正切分别为：sinα ＝ y/r，cosα ＝ x/r，tanα ＝ y/x（x ≠ 0）。

4、三角函数线有正弦线、余弦线、正切线，它们分别是角α的终边与单位圆交点的纵坐标、横坐标、纵坐标与横坐标的比值。

二、同角三角函数的基本关系1、平方关系：sin²α ＋cos²α ＝ 12、商数关系：tanα ＝sinα/cosα三、诱导公式诱导公式可以将任意角的三角函数转化为锐角的三角函数。

例如：sin(π ＋α) ＝sinα，cos(π α) ＝cosα 等。

四、三角函数的图象和性质1、正弦函数 y ＝ sin x图象：是一条波浪形曲线，周期为2π，对称轴为 x ＝kπ ＋π/2（k∈Z），对称中心为(kπ, 0)（k∈Z）。

性质：在π/2 ＋2kπ, π/2 ＋2kπ（k∈Z）上单调递增，在π/2 ＋2kπ, 3π/2 ＋2kπ（k∈Z）上单调递减。

2、余弦函数 y ＝ cos x图象：也是一条波浪形曲线，周期为2π，对称轴为 x ＝kπ（k∈Z），对称中心为(π/2 ＋kπ, 0)（k∈Z）。

性质：在π ＋2kπ, 2kπ（k∈Z）上单调递增，在2kπ, π ＋2kπ（k∈Z）上单调递减。

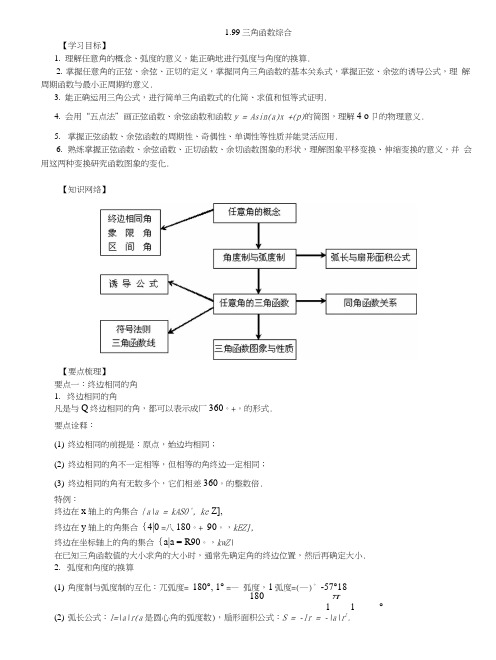
1.99三角函数综合【学习目标】1.理解任意角的概念、弧度的意义，能正确地进行弧度与角度的换算.2.掌握任意角的正弦、余弦、正切的定义，掌握同角三角函数的基本关系式，掌握正弦、余弦的诱导公式，理解周期函数与最小正周期的意义.3.能正确运用三角公式，进行简单三角函数式的化简、求值和恒等式证明.4.会用“五点法”画正弦函数、余弦函数和函数y = Asin(a)x +(p)的简图，理解4 o卩的物理意义.5.掌握正弦函数、余弦函数的周期性、奇偶性、单调性等性质并能灵活应用.6.熟练掌握正弦函数、余弦函数、正切函数、余切函数图象的形状，理解图象平移变换、伸缩变换的意义，并会用这两种变换研究函数图象的变化.【知识网络】【要点梳理】要点一：终边相同的角1.终边相同的角凡是与Q终边相同的角，都可以表示成厂360。

+。

的形式.要点诠释：(1)终边相同的前提是：原点，始边均相同；(2)终边相同的角不一定相等，但相等的角终边一定相同；(3)终边相同的角有无数多个，它们相差360。

的整数倍.特例：终边在x轴上的角集合｛a\a = kAS0°, ke Z],终边在y轴上的角集合｛4|0 =八180。

+ 90。

，kEZ],终边在坐标轴上的角的集合｛a|a = R90。

，kwZ\在已知三角函数值的大小求角的大小时，通常先确定角的终边位置，然后再确定大小.2.弧度和角度的换算(1)角度制与弧度制的互化：兀弧度= 180°, 1°=—弧度，1弧度=(―)° -57°18180 7T1 1 °(2)弧长公式：l=\a\r(a是圆心角的弧度数)，扇形面积公式：S = -lr = -\a\r2.2 2要点诠释：(1)角有正负零角之分，它的弧度数也应该有正负零之分，如-龙,-2兀等等，一般地，正角的弧度数是一个正数，负角的弧度数是一个负数，零角的弧度数是0,角的正负主要由角的旋转方向来决定.(2)角a的弧度数的绝对值是: ,其中，/是圆心角所对的弧长，尸是半径.要点二：任意角的三角函数的定义、三角函数的符号规律、特殊角的三角函数值、同角三角函数的关系式、诱导公式：1•三角函数定义：角a终边上任意一点户为(兀刃，设| OP |= r则：. v x ysma = —, cos a = —, tan a- —r r x要点诠释：三角函数的值与点P在终边上的位置无关，仅与角的大小有关•我们只需计算点到原点的距离r = Jx2 + v2 ,如/ •v x y那么sin a - t, cosa = —p tan =—.7^77 7^77 x2.三角函数符号规律：一全正，二正弦，三正切，四余弦(为正)；a a要点诠释：口诀的含义是在第一象限各三角函数值为正；在第二象限正弦值为正，在第三象限正切值为正，在第四象限余弦值为正..特殊角的三角函数值同角三角函数的基本关系：• o 7 . sin asirr G + cos~ a -1; ------- = tan acos a要点诠释：(1)这里“同角”有两层含义，一是“角相同”，二是对“任意” 一个角(使得函数有意义的前提下)关系式都成(2) sin 2。

初中数学锐角三角函数综合复习讲义一、研究概念1、产生的背景：直角三角形的边与角之间的关系2、明确概念：正弦阐述概念：在直角三角形中，锐角A 的对边与斜边的比叫做锐角A 的正弦，记作sinA 3、本质：特殊的实数 4、知识点产生的条件： [直角三角形] 直角三角形中任意两边和任意一锐角5、特征： 正弦 [定义] 在△ABC 中，∠C 为直角，我们把锐角A 的对边与斜边的比叫做∠A 的正弦 →[表示法] sinA=∠A 的对边斜边[特殊字母] sinA=a c sinB=bc(∠A+∠B=90°) 余弦 [定义] 在△ABC 中，∠C 为直角，我们把锐角A 的邻边与斜边的比叫做∠A 的余弦→[表示法] cosA=∠A 的邻边斜边[特殊字母] cosA=bccosB=a c (∠A+∠B=90°)sinA=ac = cosB= cos (90°—∠A) cosA=bc= sinB= sin (90°—∠A)定义] 在△ABC 中，∠C 为直角，我们把锐角A 的对边与邻边的比叫做∠A 的正切→[表示法] tanA=∠A 的对边邻边特殊字母] tanA=abtanB=b a (∠A+∠B=90°)余切 [定义] 在△ABC 中，∠C 为直角，我们把锐角A 的邻边与对边的比叫做∠A 的余切→[表示法] cotA=∠A 的邻边对边[特殊字母] cotA=b a cotB= ab(∠A+∠B=90°) tanA=ab= cotB= cot (90°—∠A) CBA c bacotA=ba= tanB= tan (90°—∠A) [文字] 一个角的正弦等于它余角的余弦 一个角的余弦等于它余角的正弦一个角的正切等于它余角的余切一个角的余切等于它余角的正切[勾股] sin 2 A+ cos 2A= 1 sin 2 B+ cos 2B= 1[运算] tanA ·cotA=1 tanB · cotB=1[正弦、余弦] tanA=sin A cosA cotA=cos AsinA tanB=cos A sinA cotB=sin AcosA[特殊值] sin30°=cos60°=12sin45°=cos45°=2若α、β是锐角，且α＞β，则sin60°=cos30°α＞sin β cos α＜cos βtan30°=cot60°α＞tan β cot α＜cot β tan45°=cot45°= 1tan60°=cot30°6、系统找下位含有特殊角的斜三角形∍内角是特殊角∍15°，30°，45°，60°，90° 外角是特殊角∍15°，30°，45°，60°，90°二、应用、例题讲解（一）直角三角形中，已知两边求锐角三角函数 1、在中，∠C 为直角，已知a=3，b=4，则cos B= （ ） (A 级)对象：cos B 角度：cos B=a c分析：a=3，b=4 [勾股] c=5 cos B=a c =35（二）直角三角形中，已知一锐角的三角函数求锐角的其它三角函数 2、∠A 为锐角，且sinA=135，则tanA 的值为 （ ） （A 级） A 、512 B 、1213 C 、1312 D 、125对象：tanA 角度 ： tanA=sin AcosA分析：sinA=135 [sin 2 A+ cos 2A= 1] cos 2A= 1－ sin 2A cosA=1312 [tanA=sin A cosA ] tanA= 1253、设x 为锐角，且满足 sin x=3cos x ，则sin x ·cos x 等于 (B 级)对象：sin x ·cos x 角度：sin 2x+ cos 2x= 1分 析：sin x=3cos x [sin 2x+ cos 2x= 1] (3cos x)2＋cos 2x= 1 cos 2x=101 sin x ·cos x= 3cos 2x=103 4、如果x= tanA+1,y=cotA+1(A 为锐角)，那么y 等于 (B 级) 对象： y 角度：tanA · cotA=1分析：x= tanA+1,y=cotA+1 [tanA · cotA=1] （x-1）(y-1)=1y=1-x x 5、如果A 为锐角，且 sinA=54，那么 （ ） (B 级) A 、0°〈 A ≤30° B 、30°〈A ≤45° C 、45°〈A 〈60° D 、60°〈A 〈90°对象：A 角度：sinA=54 分析：22〈54〈23 sin 45°〈sinA 〈sin60° ∵A 为锐角 ～ 0°〈 A 〈90° 此时 sinA 是增函数 ∴ 45°〈A 〈60°6、已知A 为锐角，且2cos sin 2cos 2sin 3=-+AA AA ，那么tanA 的值等于 (B 级)对象：tanA 角度：tanA=sin AcosA分析：2cos sin 2cos 2sin 3=-+A A A A 3 sinA+2cosA=4sinA -2cosA sinA=4cosA sin AcosA=4=tanA7、在 中，c 为斜边，a 、b 为直角边，则a 3 cosA+b 3cosB 等于 （B 级）对象：a 3 cosA+b 3cosB 角度 ：cosA=∠A 的邻边斜边勾股定理分析 ：a 3cosA+b 3cosB = a 3·b c + b 3·a c =cabc 2 = abc8、计算： （A 级）对象： 角度 ：特殊角的三角函数值分析：=213222∙+⎪⎪⎭⎫ ⎝⎛=231+ 9、计算：sin 248°+sin 242°-tan44°·tan45°·tan46°= （B 级）对象：sin 248°+sin 242°-tan44°·tan45°·tan46°角度：sinA= cos (90°—∠A) tanA= cot (90°—∠A)分析：sin48°=cos(90°－48°)=cos42° tan 44°=cot(90°－44°)=cot46°原式= cos 242°+ sin 242°－cot46°·tan46°·tan45°=1－1·1=010、如图，CD 是平面镜，光线从A 点出发经CD 上点E 反射到B 点，若入射角为α（入射角等于反射角），AC ⊥CD ，BD ⊥CD ，垂足分别为C 、D ，且AC=3，BD=6，CD=11。

三角函数与三角恒等变换的综合运用三角函数和三角恒等变换是数学中的重要概念，广泛应用于各种实际问题的求解中。

本文将探讨三角函数和三角恒等变换的综合运用，并通过一些实例来说明它们在实际问题中的应用。

一、三角函数的基本概念在介绍三角函数的综合运用之前，我们首先回顾一下三角函数的基本概念。

在直角三角形中，对于给定的一个角A，我们可以定义其正弦、余弦和正切等三个三角函数，分别记作sinA，cosA和tanA。

它们的定义如下：sinA = 对边/斜边cosA = 邻边/斜边tanA = 对边/邻边二、三角函数的综合运用1. 三角函数在三角形的计算中的应用三角函数在求解三角形的各种问题中起着重要的作用。

以求解三角形边长为例，假设我们已知一个直角三角形的一条边和其对应的一个角，利用三角函数可以很方便地求解出另外两条边的长度。

同样地，在已知两边和夹角的情况下，我们也可以利用三角函数来求解三角形的面积。

2. 三角函数在物理问题中的应用三角函数在物理问题中的应用广泛而重要。

例如，在力学中，一个物体在平面上做直线运动时，我们可以将其位移的x轴和y轴分解为其在x轴和y轴上的分量。

而这些分量之间恰好是两个相互垂直的直角三角形，通过使用三角函数，可以很容易地求解出物体的位移和速度等物理量。

三、三角恒等变换的应用1. 三角恒等变换在三角方程的求解中的应用三角恒等变换在解三角方程时起到了至关重要的作用。

通过利用一些特定的三角恒等变换，我们可以将复杂的三角方程化简为简单的等式，从而更方便地求解。

例如，通过应用和差化积公式和倍角公式，我们可以将一些复杂的三角方程转化为简单的线性方程或二次方程，进而求解出未知量。

2. 三角恒等变换在三角函数的化简中的应用三角恒等变换在化简三角函数表达式时也起到了重要的作用。

通过运用正弦、余弦和正切的平方恒等变换、和差化积公式等，我们可以将复杂的三角函数表达式化简为简单的形式，从而方便计算和求解。

这对于在数学推导和物理计算中的精确性和效率都很重要。

三角函数最全知识点总结三角函数是高中数学中的重要内容，主要包括正弦函数、余弦函数、正切函数等。

下面将对这些三角函数的定义、性质以及常用的解题方法进行总结。

一、正弦函数（sin）：1. 定义：在单位圆上，任选一点P与x轴正方向的夹角为θ，P点的纵坐标y即为θ的正弦值，记作sinθ。

正弦函数的定义域为实数集，值域为[-1,1]。

2. 周期性：sin(θ+2π)=sinθ，sin(θ+π)=-sinθ。

其中π为圆周率。

3. 奇偶性：sin(-θ)=-sinθ，即正弦函数关于原点对称。

4. 正负性：当θ为锐角时，sinθ>0；当θ为钝角时，sinθ<0。

5. 值域变化：当θ从0增加到π/2时，sinθ从0增加到1，然后再从1减小到0。

二、余弦函数（cos）：1. 定义：在单位圆上，任选一点P与x轴正方向的夹角为θ，P点的横坐标x即为θ的余弦值，记作cosθ。

余弦函数的定义域为实数集，值域为[-1,1]。

2. 周期性：cos(θ+2π)=cosθ，cos(θ+π)=-cosθ。

3. 奇偶性：cos(-θ)=cosθ，即余弦函数关于y轴对称。

4. 正负性：当θ为锐角时，cosθ>0；当θ为钝角时，cosθ<0。

5. 值域变化：当θ从0增加到π/2时，cosθ从1减小到0。

三、正切函数（tan）：1. 定义：正切值tanθ等于θ的正弦值除以θ的余弦值，即tanθ=sinθ/cosθ。

正切函数的定义域为实数集，值域为实数集。

2. 周期性：tan(θ+π)=tanθ。

3. 奇偶性：tan(-θ)=-tanθ，即正切函数关于原点对称。

4. 正负性：当θ为锐角时，tanθ>0；当θ为钝角时，tanθ<0。

四、反三角函数：1. 反正弦函数：定义域为[-1,1]，值域为[-π/2，π/2]。

记作arcsin x或sin⁻¹x。

2. 反余弦函数：定义域为[-1,1]，值域为[0,π]。

三角函数的复习与综合问题解答一、引言三角函数是数学中重要的概念之一，其在几何图形的研究、物理学中的波动问题等方面都有广泛应用。

本文将对三角函数的基本概念进行复习，并针对一些综合问题进行解答，以帮助读者加深对三角函数的理解与应用。

二、对三角函数的复习1. 正弦函数正弦函数是三角函数中最基本的函数之一。

在直角三角形中，正弦函数定义为斜边与对应角的比值。

其函数表示为sin(x)，其中x为角度或弧度。

2. 余弦函数余弦函数也是三角函数中的重要函数。

在直角三角形中，余弦函数定义为邻边与斜边的比值。

其函数表示为cos(x)，其中x为角度或弧度。

3. 正切函数正切函数定义为正弦函数与余弦函数的比值，表示为tan(x)，其中x为角度或弧度。

4. 反三角函数反三角函数是三角函数的反函数，用于求解角度的函数。

常见的反三角函数有反正弦函数（表示为arcsin(x)或sin^(-1)(x)）、反余弦函数（表示为arccos(x)或cos^(-1)(x)）以及反正切函数（表示为arctan(x)或tan^(-1)(x)）等。

三、综合问题解答1. 问题一：已知正弦函数sin(x)=1/2，求解x的值。

解答：根据正弦函数的定义可知，sin(x)等于对边与斜边的比值。

所以，我们可以得到一个特殊角的sin值为1/2，即30度或π/6。

因此，x的解为30度或π/6。

2. 问题二：已知余弦函数cos(x)=√3/2，求解x的值。

解答：根据余弦函数的定义可知，cos(x)等于邻边与斜边的比值。

所以，我们可以得到一个特殊角的cos值为√3/2，即60度或π/3。

因此，x的解为60度或π/3。

3. 问题三：已知正切函数tan(x)=1，求解x的值。

解答：根据正切函数的定义可知，tan(x)等于对边与邻边的比值。

所以，我们可以得到一个特殊角的tan值为1，即45度或π/4。

因此，x的解为45度或π/4。

4. 问题四：已知tan(x)=√3，求解x的值。

中考总复习锐角三角函数综合复习--知识讲解锐角三角函数是初中数学中的一个重要内容，也是中考数学考试中常考的内容之一、掌握了锐角三角函数的定义、性质和相关的计算方法，可以帮助我们解决与角度有关的各种问题，如计算角度的大小、求角的三角函数值等。

下面是锐角三角函数的综合复习知识讲解。

1.弧度制和角度制在介绍锐角三角函数之前，我们首先要了解弧度制和角度制。

在角度制中，一个圆的周长被定义为360度，而在弧度制中，一个圆的周长被定义为2π弧度。

所以可以得到以下关系：360度=2π弧度180度=π弧度90度=π/2弧度2.定义对于任意一个锐角A，我们可以在一个单位圆上面取点P，使得∠POA 的顶点为O，点O为圆心，点P在单位圆上。

这样，我们可以定义以下几个锐角三角函数：正弦函数sinA、余弦函数cosA、正切函数tanA、余切函数cotA。

3.性质(1) 正弦函数sinA：在单位圆上，点P的纵坐标就是正弦值sinA。

(2) 余弦函数cosA：在单位圆上，点P的横坐标就是余弦值cosA。

(3) 正切函数tanA：tanA的值等于sinA/cosA。

(4) 余切函数cotA：cotA的值等于cosA/sinA。

(5) 错位现象：sinA等于cos(90度-A)，cosA等于sin(90度-A)。

4.基本关系式(1) sin²A + cos²A = 1，即sin²A = 1 - cos²A，cos²A = 1 -sin²A。

(2) tanA = sinA/cosA，cotA = 1/tanA = cosA/sinA。

(3) sin(180度 - A) = sinA，cos(180度 - A) = -cosA。

(4) cos(360度 - A) = cosA，sin(360度 - A) = -sinA。

5.锐角三角函数的值(1)0度、30度、45度、60度、90度的正弦、余弦、正切值是特殊的，需要进行熟记。