兴化市第一中学2018秋学期数学高三期初检测

兴化市第一中学2018秋学期高二月考试卷数学（文科）试题（全卷满分160分，考试时间120分钟）2018.6卷面分值：160分考试时间：120分钟一、填空题（每小题5分，共计70分.请将答案写在答题纸指定区域）1.已知集合}3,2,1{},1,2{-=--=BA，则=⋂BA▲．2.函数xy ln1-=的定义域为▲．3.命题“若，则”的逆否命题是_____▲_____.4.如果幂函数的图象不过原点，则m的值是▲．5.某校共有400名学生参加了一次数学竞赛，竞赛成绩都在[50，100]内，且频率分布直方图如图所示(成绩分组为[50，60)，[60，70)，[70，80)，[80，90)，[90，100]，则在本次竞赛中，得分不低于80分的人数为▲．6.如图是一个算法流程图，则输出的a的值是▲．7.某单位要在4名员工(含甲、乙两人)中随机选2名到某地出差，则甲、乙两人中，至少有一人被选中的概率是▲．8.已知偶函数)(xf满足bfaf=-'=')1(,)1(，则a + b= ▲ ．9.用系统抽样法从160名学生中抽取容量为20的样本，将160名学生从1160~编号，按编号顺序平均分成 20组(18~号，916~号，,153160~号).若假设第1组抽出的号码为3，则第5组中确定的号码是_____ ▲．10.函数1323+-=xxy在[–1，3]上的最大值是▲ .11．已知命题p :|x －a |<4,命题q :(x －1)(2－x )>0,若p 是q 的必要不充分条件,则实数a 的取值范围是 ▲ ．12．已知存在实数a ，满足对任意的实数b ，直线y x b =-+都不是曲线33y x ax =-的切线，则实数a 的取值范围是 ▲ .13. 已知函数222,0()0,0,0x x x f x x x mx x ⎧-+>⎪==⎨⎪+<⎩是奇函数且函数f (x )在区间[－1，a －2]上单调递增，则实数a 的取值范围为 ▲ ．14.设函数a ax x e x f x+--=)12()(，其中1<a ，若仅存在两个的整数21,x x 使得0)(1<x f ，0)(2<x f ，则实数a 的取值范围是 ▲ ．二、解答题（本大题共6个小题，共90分,需写出必要的解题过程） 15.（本题满分14分)（1）求值： 32log 5333322log 2log log 839+-+-； （2）设()f x =，求()()1f x f x +-的值.16.(本题满分14分)设命题p ：01)3(2,2=+--∈∃x m x R x ，命题q ：0193)5(2,2≠+++-∈∀m x m x R x ． （1）若q p ∧为假命题，求实数m 的取值范围；（2）若q p ∨为真命题，且q p ∧为假命题，求实数m 的取值范围．17.（本题满分14分)设函数()()22,f x x bx c b c R =++∈.（1）若b 和c 分别是先后抛掷一枚骰子得到的点数，求对任意x R ∈， ()0f x >恒成立的概率；（2）若b 是从区间[]0,10任取的一个数， c 是从[]0,4任取的一个数，求函数()f x 的图像与x 轴有交点的概率.18.（本题满分16分)已知美国苹果公司生产某款iphone 手机的年固定成本为40万美元，每生产1只还需另投入16美元．设苹果公司一年内共生产该款iphone 手机x 万只并全部销售完，每万只的销售收入为R （x ）万美元，且R （x ）=（1）写出年利润W （万元）关于年产量x （万只）的函数解析式；（2）当年产量为多少万只时，苹果公司在该款手机的生产中所获得的利润最大？并求出最大利润．19.(本大题满分16分)已知函数aa x f x x -+⋅=212)(（a 为常数）．（1）证明：a =1是函数)(x f 为奇函数的充分不必要条件； （2）如果存在R x ∈0，使得)(0x f =1，求a 的取值范围； （3）若)(x f 在[0, 1]上是单调递减函数，求a 的取值范围．20.(本大题满分16分)已知函数R a x ax x x f ∈+-=,21ln )(2. (1) 若0)1(=f ，求函数f(x)的单调减区间；若关于x 的不等式1)(-≤ax x f 恒成立，求整数a 的最小值；（3）若2-=a ，正实数21,x x 满足0)()(2121=++x x x f x f ，证明：21521-≥+x x . 文科答案1. }1{-2. ],0(e3.若，则4. 15. 1206. 1277.658.0 9. 35 10. 1 11． [－2,5] 12． a <13 13. (1，3] 14. )23,35[2ee 二、解答题（本大题共6个小题，共90分,需写出必要的解题过程） 15.（本题满分14分)16.(本题满分14分)解：（1）若命题p 正确，则4m ≥或2m ≤， ……………………………………2分 若命题q 正确，则61m -<<-， ……………………………………4分 则p q ∧为真命题时，则61m -<<-所以若p q ∧为假命题，则实数m 的取值范围为(,6][1,)-∞--+∞…………………7分 （2）如果p q ∨为真命题，则4m ≥或2m ≤，………………………………………10分 又p q ∧为假命题，(,6][1,)m ∈-∞--+∞，则所求的实数m 的取值范围为(,6][1,2][4,)-∞--+∞． ………………………14分 17.（本题满分14分)解：（1）利用利润等于收入减去成本，可得=﹣6x 2+384x ﹣40；当x ＞40时，W=xR （x ）﹣当0＜x ≤40时，W=xR （x ）﹣（16x +40）（16x +40）=∴W=；（2）当0＜x ≤40时，W=﹣6x 2+384x ﹣40=﹣6（x ﹣32）2+6104，∴x=32时，W max =W （32）=6104；当x ＞40时，W=≤﹣2+7360，当且仅当，即x=50时，W max =W （50）=5760∵6104＞5760∴x=32时，W 的最大值为6104万美元． 18.(本题共满分16分)19.(本大题满分16分)解：（1）由aa x f x x -+⋅=212)(是奇函数，知)()(x f x f -=-，整理得，22[(2)1](1)0x a +-=，即1±=a ， ……………………………………4分 且每步可逆，所以，1±=a 是函数)(x f 为奇函数的充分必要条件，所以1=a 是函数)(x f 为奇函数的充分不必要条件．……………………………………6分（2）由1212)(000=-+⋅=a a x f x x ，得)1,1(12211212000-∈+-=+-=x x x a ． …………12分 （3）因为aa a a a x f x x x -++=-+⋅=21212)(2在]1,0[上是单调递减函数，所以a x-2在]1,0[单调递增，且02>-a x或02<-a x在]1,0[上恒成立，故1<a 或2>a ． ……………………………………16分 20. 解：(1) 因为f(1)＝1－a2＝0，所以a ＝2.(1分)此时f(x)＝lnx －x 2＋x ，x>0，f ′(x)＝1x －2x ＋1＝－2x 2＋x ＋1x(x>0)．…………………(2分)由f′(x)<0，得2x 2－x －1>0.又x>0，所以x>1.所以f(x)的单调减区间为(1，＋∞)．……………………(4分) (2) 解：(解法1)令g(x)＝f(x)－(ax －1)＝lnx －12ax 2＋(1－a)x ＋1，所以g′(x)＝1x －ax ＋(1－a)＝－ax 2＋（1－a ）x ＋1x.当a ≤0时，因为x>0，所以g′(x)>0.所以g(x)在(0，＋∞)上是增函数． 因为g(1)＝ln1－12a ×12＋(1－a)＋1＝－32a ＋2>0，所以关于x 的不等式f(x)≤ax －1不能恒成立．……………………(6分)当a>0时，g ′(x)＝xx a x a x x a ax x g )1)(1(1)1()(2+--=+-+-=' 令g′(x)＝0，得x ＝1a .所以当x ∈)1,0(a 时，g ′(x)>0；当x ∈),1(+∞a时，g ′(x)<0，因此函数g(x)在)1,0(a 上是增函数，在),1(+∞a上是减函数． 故函数g(x)的最大值为a aa a a a a a g ln 2111)1()1(211ln)1(2-=+⨯-+⨯-= ……(8分) 令h(a)＝12a －lna ，因为h(1)＝12>0，h(2)＝14－ln2<0，又h(a)在a ∈(0，＋∞)上是减函数．故当a ≥2时，h(a)<0.所以整数a 的最小值为2.……………………(10分)(解法2)由f(x)≤ax －1恒成立，得lnx －12ax 2＋x ≤ax －1在(0，＋∞)上恒成立，问题等价于a ≥lnx ＋x ＋112x 2＋x 在(0，＋∞)上恒成立．令g(x)＝lnx ＋x ＋112x 2＋x ，只要a ≥g(x)max .……………………(6分)因为22)21()ln 21)(1()(x x x x x x g +--+=' 令g′(x)＝0，得－12x －lnx ＝0. 设h(x)＝－12x －lnx ，因为h′(x)＝－12－1x<0，所以h(x)在(0，＋∞)上单调减，不妨设－12x －lnx ＝0的根为x 0.当x ∈(0，x 0)时，g ′(x)>0；当x ∈(x 0，＋∞)时，g ′(x)<0，所以g(x)在x ∈(0，x 0)上是增函数；在x ∈(x 0，＋∞)上是减函数．所以=+++==020000max 211ln )()(x x x x x g x g 00001)211(211x x x x =++……………………(8分) 因为)21(h ＝ln2－14>0，h(1)＝－12<0，所以12<x 0<1，此时1<1x 0<2，即g(x)max ∈(1，2)．所以a ≥2，即整数a 的最小值为2.……………………(10分)(3) 证明：当a ＝－2时，f(x)＝lnx ＋x 2＋x ，x>0，由f(x 1)＋f(x 2)＋x 1x 2＝0，即lnx 1＋x 21＋x 1＋lnx 2＋x 22＋x 2＋x 1x 2＝0,从而(x 1＋x 2)2＋(x 1＋x 2)＝x 1x 2－ln(x 1x 2)．……………………(13分) 令t ＝x 1x 2，则由φ(t)＝t －lnt 得，φ′(t)＝t －1t，可知，φ(t)在区间(0，1)上单调减，在区间(1，＋∞)上单调增． 所以φ(t)≥φ(1)＝1，(x 1＋x 2)2＋(x 1＋x 2)≥1， 故x 1＋x 2≥5－12成立．……………………(16分)． (2)。

江苏省泰州市兴化一中2018届高考第四次模拟考试数学试卷一、填空题1．已知集合}{1,1,2A =-，{}13B x x =-<<，则A B =I ▲ ． 2．已知复数12i z =+，其中i 是虚数单位，则z 的模为 ▲ ． 3．已知一组数据4，3，5，7，1，则该组数据的方差为 ▲ ． 4．执行如图所示的伪代码，最后输出的a 的值是 ▲ ．5．从1,2,3,4,5中任取2个不同的数，则取到的2个数的和大于5的概率为 ▲ ． 6．已知sin 2cos 0αα+=，则tan 2α= ▲ ．7．在平面直角坐标系xOy 中，双曲线2211x y m -=+的离心率为2，则实数m 的值是 ▲8．在三棱锥S ABC -中，直线SA ⊥平面ABC ，1SA =，ABC ∆的面积为3，若点G 为ABC ∆的重心，则三棱锥S AGB -的体积为 ▲ ．9．已知1130,15n n θθθ+=︒=+︒，1sin n n a θ+=，N *n ∈，则224a a += ▲ ． 10．在平面直角坐标系xOy 中，若圆2220x y x ay +-+=与曲线220x y -=有2个公共点，则实数a 的值是 ▲ ．11．已知定义在区间[2,2]-的函数()f x 满足1(2)()2f x f x +=，当20x -≤<时，2()f x x x =-，则不等式()f x x ≤的解集为 ▲ ．12．已知函数11()1,()(())k k f x x f x f f x +=-=，其中N k *∈，且6k ≤，若方程()ln 0k f x x -=恰有两个不相等的实数根，则k 的取值集合为 ▲ ．13.在ABC ∆中，点D ，E 分别在线段AC ，BC 上，⋅=⋅，若,AE BD 相交于点F 3=，则=⋅ ▲ ．14. 在ABC ∆中，角,,A B C 的对边分别为,,a b c ，若2s i n s i n 2s i n C B A =，且3s i n bB a=，则实数m 的最小值是 ▲ ． 二、解答题15．在ABC ∆中,已知角,,A B C 的对边分别为,,a b c . 且满足sin()sin()sin()333b Cc B a A πππ+-+=+.（1）若b c =，求A ；（2）若3A π=，a =sin()B C -的值.16．已知三棱锥P ABC -中，AB AC ⊥，AB PC ⊥.（1）求证：AB ⊥平面PAC ；（2）若平面α分别与棱PA 、PB 、BC 、AC 相交于点E 、F 、G 、H ，且//PC 平面α， 求证：//EH FG .17．如图，建筑公司受某单位委托，拟新建两栋办公楼AB ，CD （AC 为楼间距），两楼的楼高分别为 m a ， m b ，其中b a >．由于委托单位的特殊工作性质，要求配电房设在AC 的中点M 处，且满足两个设计要求：① 90BMD ∠=︒，②楼间距与两楼的楼高之和的比(0.8,1)λ∈．（１）求楼间距AC （结果用,a b 表示）；（２）若45CBD ∠=︒，是否能满足委托单位的设计要求？18．已知椭圆:C 22221(0)x y a b a b +=>>的离心率为，一条准线方程为2x =．过点(0,2)P 且不与y 轴垂直的直线l 与椭圆C 相交于,A B 两点．线段AB 的中点为D ，点Q 为y 轴上一点，且满足QA QB =．（1）求椭圆C 的方程；（2）求证：线段QD 的中点在定直线上； （3）若ABQ ∆为等边三角形，求直线l 的方程．19．已知函数()xf x xe ax =-，R a ∈． (1)当0a =时，求()f x 的最小值；（2）若0x ≥时，2()f x ax ≥恒成立，求实数a 的取值范围；（3）若函数()f x 存在极小值，求实数a 的取值范围．20．已知数列}{n a 的前n 项和为n S ．数列}{n b 满足21n n n S b b ++=，N*n ∈． （1）若2n n b =，且8m S =，求正整数m 的值； （2）若数列}{n a ，}{n b 均是等差数列，证明：10b ≥；（3）若数列}{n a 是等比数列，公比为q ，且111a q b ->>≥，是否存在正整数k ，使1b ，341k b +，k b 成等差数列，若存在，求出一个k 的值，若不存在，请说明理由．附加题21. （［选做题］请考生在A 、B 、C 、D 四小题中任选两题作答，如果多做，则按所做的前两题记分．A ．（几何证明选讲）如图，已知AD 是ABC ∆的角平分线，圆O 过,A D 且与BC 相切与点D ，圆O 分别与,AB AC 相交于,E F . 求证：AE CF AF BE ⋅=⋅.B ．（本小题满分10分，矩阵与变换） 已知矩阵111A a ⎡⎤=⎢⎥⎣⎦，在平面直角坐标系xOy 中，直线:30l x y ++=在矩阵1A -对应的变换下得到直线:10l x by '++=，求实数a ，b 的值．C ．（本小题满分10分，坐标系与参数方程选讲） 己知在平面直角坐标系xOy 中，曲线C 的参数方程为2cos sin x y αα=⎧⎨=⎩（α为参数）．以原点O为极点，以x 轴的非负半轴为极轴的极坐标系中，直线l 的极坐标方程为(s i n c o s )ρθθ+=，直线l 与曲线C 相交于,A B 两点，求线段AB 的值．D ．（本小题满分10分，不等式选讲） 已知正实数,,x y z 满足1111x y z++=，求22x yz ++的最小值．22．【必做题】如图，在三棱锥P ABC -中，PA ⊥平面ABC ，90BAC ∠=︒，2AB =，1AC =，AP t =（0t >），点D ，E 分别为AB ，PC 的中点．(1)若异面直线AE 与CD 所成角为60︒，求t 的值；(2)记平面PDC 与平面PBC 所成的锐二面角为θ，证明：(0,30)θ∈︒︒．23. 【必做题】已知数列}{n a 的前n 项和为n S ，01n a <<．（1）若332S <，求证：123,,a a a 必可以被分为1组或2组，使得每组所有数的和小于1；（2）若12n k S +<，求证：12,,,n a a a L 必可以被分为m 组（1m k ≤≤），使得每组所有数的和小于1．【参考答案】一、填空题1．{1,2} 23．4 4．4 5．356．43 7．23 8．13 9．7410．2± 11．[1,2] 12．2,4,6{} 13. 314.【解析】由正弦定理，2c b =，∴2222222213224cos 2224a b a b a b cC abab ab +-++-===-≥，（当且仅当a 时取等号）∴0sin C <≤2212)2)sin m C ===+≥．∴m ≥（当且仅当a 时取等号），∴实数m意图：解三角形背景下两次．．使用基本不等式． 二、解答题15.解：（1）∵ b c =，∴B C =，∴ππsin()sin()33+=+b C c B ， ∵πππsin()sin()sin()333+-+=+b C c B a A ，∴πsin()03+=a A ，即πsin()03+=A ，∵(0,π)∈A ，∴ππ4π333（，）+∈A ， ∴ππ3+A =，解得2π3=A .（2）∵ π3=A ，∴2ππsin()sin()332--+=b B c B ，在ABC ∆中，由正弦定理：ππsin sin()sin sin()332+-+=B C C B A ，即113sin (sin )sin (sin )224B C C C B B -=，化简后得：sin()B C -=. 16.证明：（1）∵AB AC ⊥，AB PC ⊥. 又AC ⊂平面PAC ，PC ⊂平面PAC ，AC PC C =，∴AB ⊥平面PAC .（2）∵//PC 平面α，平面PAC 平面αEH =，PC ⊂平面PAC∴//PC EH ，同理//PC FG ， 所以//EH FG .17.解：（1）∵在ABM ∆中，2tan 2a aBMA c c ∠==， 在CDM ∆中，2tan 2b bDMC c c ∠==， ∵90BMD ∠=︒，∴90BMA DMC ∠+∠=︒，∴tan tan 1BMA DMC ∠⋅∠=，即24c a b =，∴c = （2）在CBD ∆中，过点B 作CD 的垂线，垂足为E ，∴tan a CBE c ∠=，tan b a DBE c-∠=， ∴tan tan tan tan()1tan tan CBE DBECBD CBE DBE CBE DBE∠+∠∠=∠+∠=-∠⋅∠221a b a bc c c a b a a c ab c c-+==-+--⋅，∵tan tan 451CBD ∠=︒=，∴22a c ab bc +-=，设2b k a =（1k >），由（1）可得2c ka =，∴222223242a k a k a k a +-=，即322310k k --=，设32()231f k k k =--，1k >，∴2()666(1)0f k k k k k '=-=->，∴函数()f k 单调递增，又∵70f =<，100f =>，k <<1k k <+<∴22211c k a b k k kλ===∈+++，∴(0.8,1)λ∈，∴能满足委托单位的设计要求．答：(1)楼间距AC为;(2)能满足委托单位的设计要求．18.解：(1)由题意22c a a c==，又222a b c =+，解得1a b c ===，所以椭圆C 的方程为2212x y +=．（2）显然直线l 的斜率存在，设其方程为2y kx =+，代入2212x y +=整理得2(12)860k kx +++=， 设1122(,),(,)A x y B x y ，，则12221184()221212D k kx x x k k--=+=⋅=++， 所以2242221212D D k y kx k k k -=+=⋅+=++， 所以直线QD 的方程22214()1212k y x k k k --=--++，令0x =得2212Qy k -=+， 则Q D y y =-，所以QD 的中点在定直线x 轴上． 另法：由点差法易得12OD k k =-，又1QD k k =-，所以2OD QD k k =， 所以2D QD D Dy y y x x -⋅=，即D Q y y =-，所以QD 的中点在定直线上x 轴上． （3） 由（1）得12221184()221212D k kx x x k k--=+=⋅=++，所以2412D k QD k -===+，12AB x =-=因为ABC ∆AB QD =，=，解得k =，所以直线l 的方程为2y x =+．19.解：(1) 当0a =时，()e =x f x x ，()(1e '=+）x f x x ，当1x <-时，()0f x '<，()f x 单调递减；当1x >-时，()0f x '>，()f x 单调递增， 所以当1x =-时，()f x 的最小值为1(1)e-=-f ． (2)当0x ≥时，2()f x ax≥2e e e 1⇔-≥⇔-≥⇔≤+xxxx ax ax a ax a x ， 令e ()(0)1=≥+xh x x x ，则2e ()0(1)'=≥+x x h x x ， 所以()h x 在[0,)+∞上单调递增，所以min ()(0)1h x h ==，所以1a ≤.（3）设()()(1)e '==+-x g x f x x a ，则()(2)e '=+xg x x ，令()0g x '=得2x =-，所以()g x 在(,2)-∞-上单调递减，在(2,)-+∞上单调递增，所以21()(2)e ≥-=--g x g a ， 当21e ≤-a 时，21()0e ≥--≥g x a ，即()0f x '≥，所以()f x 在R 上单调递增，无极值；当21e >-a 时，因为21(2)0e-=--<g a2213()(1)e (1)()024=+-≥+-=++>a g a a a a a a ,(易证1+a e a ≥)所以(2)()0g g a -<，所以()g x 在(2,)a -上有一个零点，记为1x ， 则1(2,)x x ∈-时，()()0f x g x '=<，则()f x 单调递减；1(,)x x a ∈时，()()0f x g x '=>，则()f x 单调递增，所以()f x 在1x x =处取得极小值综上，若函数()f x 存在极小值，则实数a 的取值范围为21(,)e -+∞． （其他解法酌情给分）20.（1）解：∵21m m m S b b ++=，∴1282(2)m m ++=，即2(2)2280m m -⋅-=， ∴24m =或22m =-（舍），∴2m =．（2）证明：设等差数列}{n a ，}{n b 的公差分别为1d ，2d ， ∴2111212(1)[(1)]2n n na d b nd b n d -+++=+- 即22221121212112()[2(12)]()022d d d n a d b d n b b d -+-++-+--=，令1,2,3n =， 得222112121211222211212121122221121212112()[2(12)]()0,224()2[2(12)]()0,229()3[2(12)]()022d d d a d b d b b d d d d a d b d b b d d d d a d b d b b d ⎧-+-++-+--=⎪⎪⎪-+-++-+--=⎨⎪⎪-+-++-+--=⎪⎩， ∴21202d d -=，……① 2112122(12)02d a d b d -++-=，……② 2112()0b b d --=，……③由③得222121120d b d b b -+-=，∴22111(2)4()0b b b ---≥，∴10b ≥，（3）解：∵数列}{n a 是等比数列，11a <-，1q >，∴0n S <，∴210n n n b b S +=->， 又1111(1)111n n n a q a a S q a q q q-==-⋅≤---，∴2211n n n n n b b S b a b +=-≥-≥，∴1n nb b +≥，∴1111221111212n n n n n n n n b b b b b b b b b b +-----=⋅⋅≥>L ，∴113122411111122k k k k k b b b b b b b +++-+>+≥+≥，∴31412k k b b b ++>， ∴不存在正整数k ，使1b ，341k b +，k b 成等差数列．附加题21.A.证明：连结ED ，因为BC 与圆O 相于点D ，所以BDE DAE ∠=∠， 因为AD 是ABC ∆的角平分线，所以DAE DAF ∠=∠，又因为DEF DAF ∠=∠，所以BDE DEF ∠=∠，所以//BC EF ，所以AE AF BE CF=，即AE CF AF BE ⋅=⋅. 21. B.解：由题意可得直线l '上任意一点(,)x y ''在矩阵111A a ⎡⎤=⎢⎥⎣⎦对应的变换下得到直线l 上任意一点(,)x y ， 111x x a y y '⎤⎤⎡⎤⎡⎡=⎥⎥⎢⎥⎢⎢'⎣⎦⎣⎣⎦⎦，∴x x y y ax y ''=+⎧⎨''=+⎩， 代入l ，()()30x y ax y ''''++++=，化简后得：:(1)230l a x y '''+++=， 与直线:10l x by '++=对比可得：12311a b +==，∴22,3a b ==． 21. C.解：曲线C ：2214x y +=，直线l ：20x y +-=， 设直线l的参数方程为2x y ⎧=⎪⎨⎪=⎩，代入曲线C，得25240t ++=，∴1t =2t =-12AB t t =-= 21. D 证明：∵111112(2)()222x y z x y z x y z++=++++28≥=．22.（1）解：以,,AB AC AP 为一组正交基底，建立空间直角坐标系A xyz -， 设(0,0,0)A ,(2,0,0)B ，(0,1,0)C ，(0,0,)P t ，(1,0,0)D ,1(0,,)22tE , ∴1(0,,)22tAE =，(1,1,0)DC =-,∵异面直线AE 与DC 所成角为60︒，则1cos 60AE DC AE DC ⋅︒==⋅ ∴1t =．（2）证明：∵(1,0,)DP t =-,(1,1,0)DC =-，(2,0,)BP t =-，(2,1,0)BC =-，设平面DPC 的一个法向量为1111(,,)n x y z =，∴1100n DP n DC ⎧⋅=⎪⎨⋅=⎪⎩，∴111100x tz x y -+=⎧⎨-+=⎩，即11111z x t y x ⎧=⎪⎨⎪=⎩，取1x t =，1(,,1)n t t =， 设平面BPC 的一个法向量为2222(,,)n x y z =，∴2200n BP n BC ⎧⋅=⎪⎨⋅=⎪⎩，∴22222020x tz x y -+=⎧⎨-+=⎩，即222222z x t y x ⎧=⎪⎨⎪=⎩，取2x t =，2(,2,2)n t t =，∵平面PDC 与平面PBC 所成的锐二面角为θ， ∴21212cos 2n n n n t θ⋅==⋅，令2132m t =+，1(0,)2m ∈∴cosθ=，∵(0,90)θ∈︒︒cos 1θ<<<，∴(0,30)θ∈︒︒．23.（1）证明：∵12332a a a ++<，若1[,1)2i a ∃∈，不妨设31[,1)2a ∈，则121a a +<，满足题意；若1(0,)2i a ∀∈，则301a <<，1201a a <+<，满足题意； 综上所述：若332S <，123,,a a a 必可以被分为１组或２组，使得每组所有数的和均小于1． （2）证明：（ⅰ）当1k =时，1n S <，满足题意；（ⅱ）假设当k p =时，命题成立， 即当12n p S +<，12,,,n a a a L 必可以被分为m 组（0m p ≤≤），使得每组所有数的和均小于1， 那么，当1k p =+时，由题意，22n p S +<， ①若1[,1)2i a ∃∈，不妨设112n a ≤<，则112n p S -+<， ∴121,,,n a a a -L 必可以被分为m 组，使得每组所有数的和均小于1， ∴121,,,,n n a a a a -L 必可以被分为1m +组，使得每组所有数的和均小于1， ②若1(0,)2i a ∀∈，不妨设12n a a a ≥≥≥L ， 若12n S <，显然满足题意， 若存在i ，使得1212n n n i a a a --++++<L ，121112n n n i n i a a a a --+-+>++++≥L ， 则12n i p S -+≤， ∴12,,,n i a a a -L 必可以被分为m 组，使得每组所有数的和均小于1， ∴121,,,,,,n i n i n a a a a a --+L L 必可以被分为1m +组，使得每组所有数的和均小于1， ∴当1k p =+时，命题也成立，由（ⅰ）（ⅱ）可知：当12n k S +<时，12,,,n a a a L 必可以被分为m 组（0m k ≤≤）， 使得每组所有数的和均小于1．。

兴化市一中2018-2019学年上学期高三数学10月月考试题班级__________ 座号_____ 姓名__________ 分数__________一、选择题1． 若P 是以F 1，F 2为焦点的椭圆=1（a ＞b ＞0）上的一点，且=0，tan ∠PF 1F 2=，则此椭圆的离心率为（ ）A ．B ．C ．D ．2． 已知函数，则（ ）(5)2()e22()2xf x x f x x f x x +>⎧⎪=-≤≤⎨⎪-<-⎩(2016)f -=A ．B ．C ．1D ．2e e 1e【命题意图】本题考查分段函数的求值，意在考查分类讨论思想与计算能力．3． 已知平面向量，，若与垂直，则实数值为（ ）(12)=，a (32)=-，b k +a b a k A ． B ． C ． D ．15-1191119【命题意图】本题考查平面向量数量积的坐标表示等基础知识，意在考查基本运算能力．4． 设集合，则A ∩B 等于（ ）A ．{1，2，5}B ．{l ，2，4，5}C ．{1，4，5}D ．{1，2，4}5． 复数（为虚数单位），则的共轭复数为（ ）2(2)i z i-=i z A ． B ． C ． D ．43i -+43i +34i +34i-【命题意图】本题考查复数的运算和复数的概念等基础知识，意在考查基本运算能力．6． 如图所示，在三棱锥的六条棱所在的直线中，异面直线共有（ ）111]P ABC -A ．2对B ．3对C ．4对D ．6对7． 高考临近，学校为丰富学生生活，缓解高考压力，特举办一场高三学生队与学校校队的男子篮球比赛．由于爱好者众多，高三学生队队员指定由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队．首发要求每个班至少1人，至多2人，则首发方案数为（ ）A ．720B ．270C ．390D ．3008． 下列命题中正确的是（）A ．若命题p 为真命题，命题q 为假命题，则命题“p ∧q ”为真命题B ．命题“若xy=0，则x=0”的否命题为：“若xy=0，则x ≠0”C ．“”是“”的充分不必要条件D ．命题“∀x ∈R ，2x ＞0”的否定是“”9． 半径R 的半圆卷成一个圆锥，则它的体积为（ ）A ．πR 3B ．πR 3C ．πR 3D ．πR 310．已知数列是各项为正数的等比数列，点、都在直线上，则数列{}n a 22(2,log )M a 25(5,log )N a 1y x =-的前项和为（）{}n a n A ．B ．C ．D ．22n-122n +-21n-121n +-11．已知集合，，则（ ）{2,1,0,1,2,3}A =--{|||3,}B y y x x A ==-∈A B = A ．B ．C ．D ．{2,1,0}--{1,0,1,2}-{2,1,0}--{1,,0,1}-【命题意图】本题考查集合的交集运算，意在考查计算能力．12．已知x ，y 满足时，z=x ﹣y 的最大值为（ ）A ．4B ．﹣4C ．0D ．2二、填空题13．命题“若1x ≥，则2421x x -+≥-”的否命题为．14．已知圆C 1：（x ﹣2）2+（y ﹣3）2=1，圆C 2：（x ﹣3）2+（y ﹣4）2=9，M ，N 分别是圆C 1，C 2上的动点，P 为x轴上的动点，则|PM|+|PN|的最小值 ．　15．已知集合{}|03,A x x x R =<∈≤，{}|12,B x x x R =-∈≤≤，则A ∪B ＝ ▲ ．16．已知是定义在上函数，是的导数，给出结论如下：()f x R ()f x '()f x ①若，且，则不等式的解集为；()()0f x f x '+>(0)1f =()xf x e -<(0,)+∞②若，则；()()0f x f x '->(2015)(2014)f ef >③若，则；()2()0xf x f x '+>1(2)4(2),n n f f n N +*<∈④若，且，则函数有极小值；()()0f x f x x'+>(0)f e =()xf x 0⑤若，且，则函数在上递增．()()xe xf x f x x'+=(1)f e =()f x (0,)+∞其中所有正确结论的序号是 ．17．圆上的点（2，1）关于直线x+y=0的对称点仍在圆上，且圆与直线x ﹣y+1=0相交所得的弦长为，则圆的方程为 ．三、解答题18．（本题满分12分）在中，已知角所对的边分别是，边，且ABC ∆,,A B C ,,a b c 72c =，又的面积为，求的值．tan tan tan tan A B A B +=A ABC ∆ABC S ∆=a b +19．设圆C 满足三个条件①过原点；②圆心在y=x 上；③截y 轴所得的弦长为4，求圆C 的方程．20．如图，在Rt △ABC 中，∠EBC=30°，∠BEC=90°，CE=1，现在分别以BE ，CE 为边向Rt △BEC 外作正△EBA 和正△CED ．（Ⅰ）求线段AD 的长；（Ⅱ）比较∠ADC 和∠ABC 的大小．21．函数。

江苏省兴化市第一中学2017-2018学年高三10月学情调研考试数学（理）试题一、填空题（本大题共14小题，每小题5分，共70分．） 1、已知集合{}1,2,4A =，{}2,4,6B =，则A B = ．2、已知集合{}02x x M =<<，集合{}1x x N =≥，实数集为R ，则()RMN =ð ． 3、若集合,,1b a a ⎧⎫A =⎨⎬⎩⎭，集合{}2,,0a a bB =+，A B =A B ，则201520a b+= ．4、函数y x a =-的图象关于直线3x =对称，则a = ．5、函数()f x =的定义域为 ． 6、若2log 13a<，则a 的取值范围是 ． 7、函数()213log 3y x x =-的单调递减区间是 ．8、已知函数()23log log 3f x a x b x =-+，若142015f ⎛⎫= ⎪⎝⎭，则()2015f = ． 9、函数()141x f x a =+-是奇函数，则实数a = ． 10、已知()()314,1l o g,1a a x a x f x x x -+<⎧⎪=⎨≥⎪⎩是R 上的减函数，则a 的取值范围是 ．11、下列4个命题1:p ()0,x ∃∈+∞，1123x x⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭；2:p ()0,1x ∃∈，1123log log x x >；3:p ()0,x ∀∈+∞，121log 2xx ⎛⎫> ⎪⎝⎭；4:p 10,3x ⎛⎫∀∈ ⎪⎝⎭，131log 2xx ⎛⎫< ⎪⎝⎭．其中的真命题是 ．12、已知集合{}2430x x x A =-+<，()12202750x a x x a x -⎧⎫⎧+≤⎪⎪⎪B =⎨⎨⎬-++≤⎪⎪⎪⎩⎩⎭，若A ⊆B ，则a 的取值范围是 ．13、已知()f x 是定义在R 上且周期为3的函数，当[)0,3x ∈时，()2122fx x x =-+，若函数()y f x a =-在区间[]3,4-上有10个零点（互不相同），则实数a 的取值范围是 ． 14、若112x a x -+≥对一切0x >恒成立，则a 的取值范围是 ． 二、解答题（本大题共6小题，共90分．解答应写出文字说明、证明过程或演算步骤．） 15、（本小题满分14分）已知命题:p 46x -≤，:q 22210x x a -+-≥（0a >），若p ⌝是q 的充分不必要条件，求a 的取值范围．16、（本小题满分14分）已知函数()xf x ax b=+（a ，b 为常数，且0b ≠），满足()21f =，()f x x =有唯一解，求函数()f x 的解析式并在平面直角坐标系中作出它的图象．17、（本小题满分14分）二次函数()f x 满足()()12f x f x x +-=且()01f =．()1求()f x 的解析式；()2在区间[]1,1-上，()y f x =的图象恒在2y x m =+的图象上方，试确定实数m的取值范围．18、（本小题满分16分）某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部CD AB 是矩形，其中2AB =米，C 1B =米，上部CDG 是等边三角形，固定点E 为AB 的中点，∆EMN 是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN 是可以给设施边框上下滑动且始终保持和AB 平行的伸缩横杆．()1设MN 与AB 之间的距离为x 米，试将∆EMN 的面积S （平方）表示成关于x的函数；()2求∆EMN 的面积S （平方米）的最大值．19、（本小题满分16分）已知函数()11f x x =-（0x >）． ()1当0a b <<，且()()f a f b =时，求11a b+的值； ()2是否存在实数a 、b （a b <），使得函数()y f x =的定义域、值域都是[],a b ？若存在，则求出a 、b 的值；若不存在，请说明理由．20、（本小题满分16分）设a 为实数，函数()22f x x x a =+-，R x ∈．()1讨论()f x 的奇偶性； ()2求()f x 的最小值．江苏省兴化市第一中学2016届高三10月学情调研考试数学（理）试题参考答案一、填空题1、{}1,2,4,62、()0,13、1-4、35、(0,6⎤⎦6、()20,1,3⎛⎫+∞ ⎪⎝⎭7、()3,+∞8、29、12 10、11,73⎡⎫⎪⎢⎣⎭11、2p ，4p 12、[]4,1-- 13、10,2⎛⎫⎪⎝⎭14、(],2-∞二、解答题。

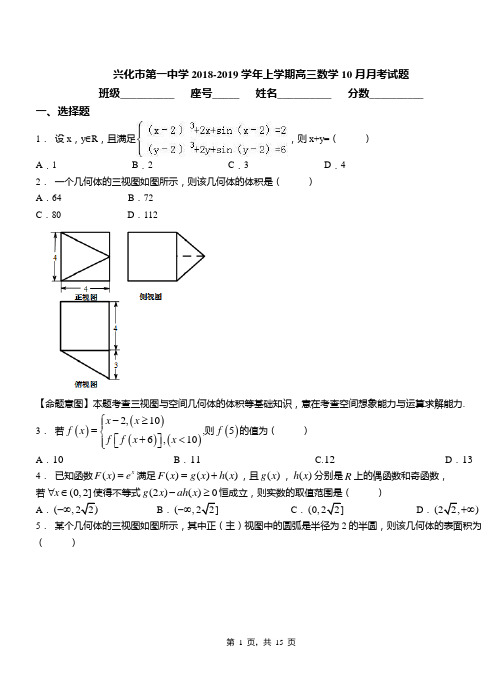
兴化市第一中学2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题1． 设x ，y ∈R，且满足，则x+y=（ ）A ．1B ．2C ．3D ．42． 一个几何体的三视图如图所示，则该几何体的体积是（ ） A ．64 B ．72 C ．80 D ．112【命题意图】本题考查三视图与空间几何体的体积等基础知识，意在考查空间想象能力与运算求解能力.3． 若()()()()2,106,10x x f x f f x x -≥⎧⎪=⎨+<⎡⎤⎪⎣⎦⎩,则()5f 的值为（ ） A ．10 B ．11 C.12 D ．134． 已知函数()xF x e =满足()()()F x g x h x =+，且()g x ，()h x 分别是R 上的偶函数和奇函数，若(0,2]x ∀∈使得不等式(2)()0g x ah x -≥恒成立，则实数的取值范围是（ ）A．(-∞ B．(-∞ C． D．)+∞ 5． 某个几何体的三视图如图所示，其中正（主）视图中的圆弧是半径为2的半圆，则该几何体的表面积为 （ ）A ．π1492+B ．π1482+C ．π2492+D ．π2482+【命题意图】本题考查三视图的还原以及特殊几何体的面积度量.重点考查空间想象能力及对基本面积公式的运用，难度中等.6． 在《张邱建算经》中有一道题：“今有女子不善织布，逐日所织的布比同数递减，初日织五尺， 末一日织一尺，计织三十日”，由此推断，该女子到第10日时，大约已经完成三十日织布总量的（ ） A ．33% B ．49% C ．62% D ．88% 7． 直线l 过点P （2，﹣2），且与直线x+2y ﹣3=0垂直，则直线l 的方程为（ ）A ．2x+y ﹣2=0B ．2x ﹣y ﹣6=0C ．x ﹣2y ﹣6=0D ．x ﹣2y+5=08． 若几何体的三视图如图所示，则该几何体的体积为（ ）A ．B ．C ．D ．π9． 设平面α与平面β相交于直线m ，直线a 在平面α内，直线b 在平面β内，且b ⊥m ，则“α⊥β”是“a ⊥b ”的（ ） A ．必要不充分条件B ．充分不必要条件C ．充分必要条件D ．既不充分也不必要条件10．如图，在棱长为1的正方体1111ABCD A B C D -中，P 为棱11A B 中点，点Q 在侧面11DCC D 内运动，若1PBQ PBD ∠=∠，则动点Q 的轨迹所在曲线为（ ）A.直线B.圆C.双曲线D.抛物线【命题意图】本题考查立体几何中的动态问题等基础知识，意在考查空间想象能力.11．2016年3月“两会”期间，有代表提出适当下调“五险一金”的缴存比例，现拟从某工厂职工中抽取20名代表调查对这一提案的态度，已知该厂青年，中年，老年职工人数分别为350，500，150，按分层抽样的方法，应从青年职工中抽取的人数为（ ） A. 5 B.6 C.7D.10【命题意图】本题主要考查分层抽样的方法的运用，属容易题.12．已知A={﹣4，2a ﹣1，a 2}，B={a ﹣5，1﹣a ，9}，且A ∩B={9}，则a 的值是（ ）A ．a=3B ．a=﹣3C ．a=±3D ．a=5或a=±3二、填空题13．设,y x 满足约束条件2110y x x y y ≤⎧⎪+≤⎨⎪+≥⎩，则3z x y =+的最大值是____________．14．已知[2,2]a ∈-，不等式2(4)420x a x a +-+->恒成立，则的取值范围为__________. 15．将一张坐标纸折叠一次，使点()0,2与点()4,0重合，且点()7,3与点(),m n 重合，则m n +的 值是 ． 16．（lg2）2+lg2•lg5+的值为 ．三、解答题17．（本小题满分12分）如图，多面体ABCDEF 中，四边形ABCD 为菱形，且60DAB ∠=，//EFAC ，2AD =，EA ED EF ===.（1）求证：AD BE ⊥；（2）若BE =-F BCD 的体积.18．对于任意的n ∈N *，记集合E n ={1，2，3，…，n}，P n =．若集合A 满足下列条件：①A ⊆P n ；②∀x 1，x 2∈A ，且x 1≠x 2，不存在k ∈N *，使x 1+x 2=k 2，则称A 具有性质Ω． 如当n=2时，E 2={1，2}，P 2=．∀x 1，x 2∈P 2，且x 1≠x 2，不存在k ∈N *，使x 1+x 2=k 2，所以P 2具有性质Ω．（Ⅰ）写出集合P 3，P 5中的元素个数，并判断P 3是否具有性质Ω． （Ⅱ）证明：不存在A ，B 具有性质Ω，且A ∩B=∅，使E 15=A ∪B ． （Ⅲ）若存在A ，B 具有性质Ω，且A ∩B=∅，使P n =A ∪B ，求n 的最大值．19．已知定义在[]3,2-的一次函数()f x 为单调增函数，且值域为[]2,7． （1）求()f x 的解析式；（2）求函数[()]f f x 的解析式并确定其定义域．20．（本小题满分12分）已知数列{}n a 的各项均为正数，12a =，114n n n na a a a ++-=+.（Ⅰ）求数列{}n a 的通项公式； （Ⅱ）求数列11n n a a +⎧⎫⎨⎬+⎩⎭的前n 项和n S ．21．某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]（Ⅰ）求图中x 的值，并估计该班期中考试数学成绩的众数；（Ⅱ）从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人，求这2人成绩均不低于90分的概率．22．一块边长为10cm的正方形铁片按如图所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器，试建立容器的容积V与x的函数关系式，并求出函数的定义域．兴化市第一中学2018-2019学年上学期高三数学10月月考试题（参考答案）一、选择题1．【答案】D【解析】解：∵（x﹣2）3+2x+sin（x﹣2）=2，∴（x﹣2）3+2（x﹣2）+sin（x﹣2）=2﹣4=﹣2，∵（y﹣2）3+2y+sin（y﹣2）=6，∴（y﹣2）3+2（y﹣2）+sin（y﹣2）=6﹣4=2，设f（t）=t3+2t+sint，则f（t）为奇函数，且f'（t）=3t2+2+cost＞0，即函数f（t）单调递增．由题意可知f（x﹣2）=﹣2，f（y﹣2）=2，即f（x﹣2）+f（y﹣2）=2﹣2=0，即f（x﹣2）=﹣f（y﹣2）=f（2﹣y），∵函数f（t）单调递增∴x﹣2=2﹣y，即x+y=4，故选：D．【点评】本题主要考查函数奇偶性的应用，利用条件构造函数f（t）是解决本题的关键，综合考查了函数的性质．2．【答案】C.【解析】3．【答案】B【解析】考点：函数值的求解.4．【答案】B【解析】试题分析：因为函数()x F x e =满足()()()F x g x h x =+,且()(),g x h x 分别是R 上的偶函数和奇函数,()()()()()()(],,,,0,222x x x xxxe e e e e g x h x eg x hx g x h x x ---+-∴=+=-∴==∀∈ 使得不等式()()20g x ah x -≥恒成立, 即22022xxxxe e e ea --+--≥恒成立, ()2222xx xxx x x x e e e e a e e e e -----++∴≤=-- ()2x x x x e e e e--=-++, 设x x t e e -=-，则函数x x t e e -=-在(]0,2上单调递增,220t e e -∴<≤-, 此时不等式222t t +≥,当且仅当2t t=,即2t =时, 取等号,22a ∴≤,故选B.考点：1、函数奇偶性的性质；2、不等式恒成立问题及函数的最值.【方法点晴】本题主要考查函数奇偶性的性质、不等式恒成立问题及函数的最值，属于难题．不等式恒成立问题常见方法：①分离参数()a f x ≤恒成立（min ()a f x ≤即可）或()a f x ≥恒成立（max ()a f x ≥即可）；②数形结合；③讨论最值min ()0f x ≥或max ()0f x ≤恒成立；④讨论参数 .本题是利用方法①求得的最大值的.5． 【答案】A6． 【答案】B 【解析】7． 【答案】B【解析】解：∵直线x+2y ﹣3=0的斜率为﹣，∴与直线x+2y ﹣3=0垂直的直线斜率为2， 故直线l 的方程为y ﹣（﹣2）=2（x ﹣2），化为一般式可得2x ﹣y ﹣6=0故选：B【点评】本题考查直线的一般式方程和垂直关系，属基础题．8． 【答案】B【解析】解：根据几何体的三视图，得该几何体是圆锥被轴截面截去一半所得的几何体， 底面圆的半径为1，高为2，所以该几何体的体积为V 几何体=×π•12×2=．故选：B ．【点评】本题考查了利用空间几何体的三视图求几何体体积的应用问题，是基础题目．9． 【答案】B【解析】解：∵b ⊥m ，∴当α⊥β，则由面面垂直的性质可得a ⊥b 成立， 若a ⊥b ，则α⊥β不一定成立， 故“α⊥β”是“a ⊥b ”的充分不必要条件， 故选：B ．【点评】本题主要考查充分条件和必要条件的判断，利用线面垂直的性质是解决本题的关键．10．【答案】C.【解析】易得//BP 平面11CC D D ，所有满足1PBD PBX ∠=∠的所有点X 在以BP 为轴线，以1BD 所在直线为母线的圆锥面上，∴点Q 的轨迹为该圆锥面与平面11CC D D 的交线，而已知平行于圆锥面轴线的平面截圆锥面得到的图形是双曲线，∴点Q 的轨迹是双曲线，故选C. 11．【答案】C12．【答案】B【解析】解：∵A={﹣4，2a ﹣1，a 2}，B={a ﹣5，1﹣a ，9}，且A ∩B={9}，∴2a ﹣1=9或a 2=9，当2a ﹣1=9时，a=5，A ∩B={4，9}，不符合题意；当a 2=9时，a=±3，若a=3，集合B 违背互异性；∴a=﹣3． 故选：B ．【点评】本题考查了交集及其运算，考查了集合中元素的特性，是基础题．二、填空题13．【答案】73【解析】试题分析：画出可行域如下图所示，由图可知目标函数在点12,33A ⎛⎫⎪⎝⎭处取得最大值为73.考点：线性规划． 14．【答案】(,0)(4,)-∞+∞【解析】试题分析：把原不等式看成是关于的一次不等式,在2]，[-2a ∈时恒成立,只要满足在2]，[-2a ∈时直线在轴上方即可，设关于的函数44)2(24)4(x f(x)y 22+-+-=-+-+==x x a x a x a 对任意的2]，[-2a ∈，当-2a =时，044)42(x )2(f(a)y 2>++--+=-==x f ，即086x )2(2>+-=-x f ，解得4x 2x ><或；当2a =时，044)42(x )2(y 2>-+-+==x f ，即02x )2(2>-=x f ，解得2x 0x ><或，∴的取值范围是{x|x 0x 4}<>或；故答案为：(,0)(4,)-∞+∞．考点：换主元法解决不等式恒成立问题.【方法点晴】本题考查了含有参数的一元二次不等式得解法，解题时应用更换主元的方法，使繁杂问题变得简洁，是易错题．把原不等式看成是关于的一次不等式,在2]，[-2a ∈时恒成立,只要满足在2]，[-2a ∈时直线在轴上方即可.关键是换主元需要满足两个条件，一是函数必须是关于这个量的一次函数，二是要有这个量的具体范围. 15．【答案】345【解析】考点：点关于直线对称；直线的点斜式方程.16．【答案】1．【解析】解：（lg2）2+lg2•lg5+=lg2（lg2+lg5）+lg5=lg2+lg5=1，故答案为：1．三、解答题17．【答案】【解析】【命题意图】本小题主要考查空间直线与直线、直线与平面的位置关系及几何体的体积等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查化归与转化思想等．（2）在EAD △中，EA ED =，2AD =，18．【答案】【解析】解：（Ⅰ）∵对于任意的n ∈N *，记集合E n ={1，2，3，…，n}，P n =．∴集合P 3，P 5中的元素个数分别为9，23，∵集合A 满足下列条件：①A ⊆P n ；②∀x 1，x 2∈A ，且x 1≠x 2，不存在k ∈N *，使x 1+x 2=k 2，则称A 具有性质Ω，∴P 3不具有性质Ω．…..证明：（Ⅱ）假设存在A ，B 具有性质Ω，且A ∩B=∅，使E 15=A ∪B ．其中E 15={1，2，3，…，15}． 因为1∈E 15，所以1∈A ∪B ，不妨设1∈A ．因为1+3=22，所以3∉A ，3∈B ．同理6∈A ，10∈B ，15∈A ．因为1+15=42，这与A 具有性质Ω矛盾． 所以假设不成立，即不存在A ，B 具有性质Ω，且A ∩B=∅，使E 15=A ∪B ．…..解：（Ⅲ）因为当n ≥15时，E 15⊆P n ，由（Ⅱ）知，不存在A ，B 具有性质Ω，且A ∩B=∅，使P n =A ∪B ． 若n=14，当b=1时，，取A 1={1，2，4，6，9，11，13}，B 1={3，5，7，8，10，12，14}， 则A 1，B 1具有性质Ω，且A 1∩B 1=∅，使E 14=A 1∪B 1．当b=4时，集合中除整数外，其余的数组成集合为，令，，则A 2，B 2具有性质Ω，且A 2∩B 2=∅，使．当b=9时，集中除整数外，其余的数组成集合，令，．则A 3，B 3具有性质Ω，且A 3∩B 3=∅，使．集合中的数均为无理数，它与P 14中的任何其他数之和都不是整数，因此，令A=A 1∪A 2∪A 3∪C ，B=B 1∪B 2∪B 3，则A ∩B=∅，且P 14=A ∪B ． 综上，所求n 的最大值为14．…..【点评】本题考查集合性质的应用，考查实数值最大值的求法，综合性强，难度大，对数学思维要求高，解题时要认真审题，注意分类讨论思想的合理运用．19．【答案】（1）()5f x x =+，[]3,2x ∈-；（2）[]()10f f x x =+，{}3x ∈-. 【解析】试题解析：（1）设()(0)f x kx b k =+>，111]由题意有：32,27,k b k b -+=⎧⎨+=⎩解得1,5,k b =⎧⎨=⎩∴()5f x x =+，[]3,2x ∈-． （2）(())(5)10f f x f x x =+=+，{}3x ∈-． 考点：待定系数法．20．【答案】（本小题满分12分） 解： （Ⅰ）由114n n n na a a a ++-=+得2214n n a a +-=，∴{}2n a 是等差数列，公差为4，首项为4， （3分）∴244(1)4n a n n =+-=，由0n a >得n a =． （6分）（Ⅱ）∵1112n n a a +==+， （9分）∴数列11n n a a +⎧⎫⎨⎬+⎩⎭的前n 项和为11111)(1)2222n +++=． （12分） 21．【答案】【解析】解：（Ⅰ）由（0.006×3+0.01+0.054+x ）×10=1，解得x=0.018，前三组的人数分别为：（0.006×2+0.01+0.018）×10×50=20，第四组为0.054×10×50=27人，故数学成绩的众数落在第四组，故众数为75分．（Ⅱ）分数在[40，50）、[90，100]的人数分别是3人，共6人， ∴这2人成绩均不低于90分的概率P==．【点评】本题考查频率分布直方图及古典概型的问题，前者要熟练掌握直方图的基本性质和如何利用直方图求众数；后者往往和计数原理结合起来考查．22．【答案】【解析】解：如图，设所截等腰三角形的底边边长为xcm ，在Rt △EOF 中，，∴， ∴依题意函数的定义域为{x|0＜x ＜10}【点评】本题是一个函数模型的应用，这种题目解题的关键是看清题意，根据实际问题选择合适的函数模型，注意题目中写出解析式以后要标出自变量的取值范围．。

兴化市第一中学2018-2019学年度第一学期期中考试高三数学试卷(考试用时:120分钟 总分:160分)一、填空题(本大题共14小题,每小题5分,共计70分)1.已知集合{}{}，，，，，，420210==B A 则=B A _______. 2.函数⎪⎭⎫ ⎝⎛-=63cos πx y 的最小正周期为________. 3.函数()12ln -=x y 的定义域为__________.4.不等式21＜xx -的解集为________. 5.已知向量()()，，，211m m =+=若，b a ⊥则=m ______. 6.曲线x e x y -=2在点(0,-1处的切线方程为_______.7.已知函数()x f 是定义在R 上的周期为2的偶函数,当10＜＜x 时,()，x x f 2log = 则=⎪⎭⎫ ⎝⎛-29f _______. 8.已知在矩形ABCD 中,AB=2,BC=1,P 是边DC 上的动点,+的最小值为______.9.已知函数()ax x x f 2cos +=在()∞+∞-，上单调递增,则实数a 的取值范围是______. 10.已知点()y x P ，的坐标满足条件，⎪⎩⎪⎨⎧≥+-≥≥0321y x x y x 则22y x +的最大值为_______.11.已知()，π⎪⎭⎫ ⎝⎛-=42cos x x f 若()，41=αf 则=αsin ______.12.(文科做)已知等差数列{}，n a 且满足:，53101=+a a 则数列{}n a 2的前10项之积为____. 12.(理科做)若()x x x f cos sin -=在[]αα，-是增函数,则α的最大值是______. 13.若函数()kx x x f -+=12只有一个零点,则实数k 的取值范围是_______.14.已知正实数y x 、满足，1=+y xx 则121++y x x 的最小值为________. 二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)15.(本题满分14分)已知函数().12+=x x x f (1)用定义证明函数()x f 在()∞+-，1上为单调递增函数； (2)若[]，，20∈x 求函数()x f 的值域。

兴化市第一中学2017学期高二期初考试试卷数学试题（全卷满分160分，考试时间120分钟）2017.9卷面分值：160分考试时间：120分钟命题人：张宇辉一、填空题（每小题5分，共计70分.请将答案写在答题纸指定区域）1.已知全集U={a，b，c，d}，集合A={a，b}，B={b，c}，则C U（A∪B）等于解：∵A={a，b}，B={b，c}，∴A∪B={a，b，c}，则∁U（A∪B）={d}，2．不等式x2﹣4x+3≤0的解集为解：（1）原不等式等价于（x﹣1）（x﹣3）≤0，所以不等式的解为1≤x≤3，即不等式x2﹣4x+3≤0的解集为{x|1≤x≤3}．…（5分）3．已知角A为三角形的一个内角，且，则tanA=【考点】两角和与差的正切函数；GG：同角三角函数间的基本关系．解：已知角A为三角形的一个内角，且，则sinA=，∴tanA==．【点评】本题主要考查两角和差的正切公式、同角三角函数的基本关系的应用，属于中档题．4．在△ABC中，已知AB=2，AC=3，A=60°．求BC的长为解：由余弦定理可得：BC2=AB2+AC2﹣2AB•ACcosA=4+9﹣2×2×3×=7，所以BC=．【点评】本题考查余弦定理的应用，正弦定理的应用，二倍角的三角函数，注意角的范围的解题的关键．5．已知数列{a n}成等比数列，若a2=4，a5=，则数列{a n}的通项公式为解：（1）设等比数列{a n}的公比为q，∵a2=4，a5=，∴，解得a1=8，q=．∴a n==2n+2．．【点评】本题考查了等比数列的通项公式及其性质，考查了推理能力与计算能力，属于中档题．6．直线3x+4y=b与圆x2+y2﹣2x﹣2y﹣2=0相切，则b=解：圆x2+y2﹣2x﹣2y﹣2=0的圆心（1，1），半径r==2，∵直线3x+4y=b与圆x2+y2﹣2x﹣2y﹣2=0相切，∴圆心（1，1）到直线3x+4y=b的距离d==2，解得b=﹣3或b=17．7．若直线=1（a＞0，b＞0）过点（1，1），则a+b的最小值等于解：∵直线=1（a＞0，b＞0）过点（1，1），∴+=1（a＞0，b＞0），所以a+b=（+）（a+b）=2++≥2+2=4，当且仅当=即a=b=2时取等号，∴a+b最小值是4，8．若直线3x﹣4y+5=0与圆x2+y2=r2（r＞0）相交于A、B两点，且∠AOB=120°（O 为坐标原点），则圆的面积为4π．解：若直线3x﹣4y+5=0与圆x2+y2=r2（r＞0）交于A、B两点，O为坐标原点，且∠AOB=120°，则圆心（0，0）到直线3x﹣4y+5=0的距离d=rcos60°=r，即=r，解得r=2，∴圆的面积为4π．9.如图，在长方体ABCD﹣A1B1C1D1中，AB=AD=3cm，AA1=2cm，则四棱锥A﹣BB1D1D的体积为6cm3．解：过A作AO⊥BD于O，AO是棱锥的高，所以AO==，所以四棱锥A﹣BB1D1D的体积为V==6．10.若变量x，y满足约束条件，则z=2x+3y的最大值为解：作出不等式对应的平面区域（阴影部分），由z=2x+3y，得y=，平移直线y=，由图象可知当直线y=经过点B时，直线y=的截距最大，此时z最大．由，解得，即B（4，﹣1）．此时z的最大值为z=2×4+3×（﹣1）=8﹣3=5，【点评】本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．11.数列，，，…的前n项和为解：由，，，…，而1，4，7，10，…，是公差为3的等差数列a n，可得通项公式a n=1+3（n﹣1）=3n﹣2．∴数列，，，…的第n项为：，可化为：，∴数列，，，…的前n项和=++…+==．12．在直角三角形ABC中，∠C=90°，AB=2，AC=1，若，则•=．解：如图所示，A（1，0），B（0，），C（0，0），∵，∴D．∴=，=（0，），∴•=0+=．故答案为：．【点评】本题考查了数量积的坐标运算性质，考查了推理能力与计算能力，属于中档题．13．已知函数f（x）=是（﹣∞，+∞）上的减函数，那么a的取值范围是解：函数f（x）=是（﹣∞，+∞）上的减函数，则有即有，解得a＜1．【点评】本题考查函数的单调性的运用，注意分段函数的分界点，考查运算能力，属于中档题．14.在平面直角坐标系xOy 中，设A 是半圆O ：x 2＋y 2＝2(x ≥0)上一点，直线OA 的倾斜角为45°，过点A 作x 轴的垂线，垂足为H ，过H 作OA 的平行线交半圆于点B ，则直线AB 的方程是________．解析 直线OA 的方程为y ＝x ，代入半圆方程得A (1,1)，∴H (1,0)，直线HB 的方程为y ＝x －1，代入半圆方程得B ⎝ ⎛⎭⎪⎫1＋32，－1＋32. 所以直线AB 的方程为y －1－1＋32－1＝x －11＋32－1，即3x ＋y －3－1＝0.兴化市第一中学2017学期高二期初考试试卷数 学 答 题 纸 命题人：张宇辉成绩一、填空题：（本大题有14小题，每小题5分，共70分。

2018届高三第四次模拟考试数学试题(考试时间：120分钟 总分：160分)注意事项：所有试题的答案均填写在答题纸上，答案写在试卷上的无效．一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．）1．已知集合，，则 ▲ ． }{1,1,2A =-{}13B x x =-<<A B =I 2．已知复数，其中是虚数单位，则的模为▲．12i z =+i z 3．已知一组数据，，，，，则该组数据的方差为 ▲43571．4．执行如图所示的伪代码，最后输出的的值是▲．a 5．从1,2,3,4,5中任取2个不同的数，则取到的2个数的和大于5的概率为 ▲ ．6．已知，则▲．sin 2cos 0αα+=tan 2α=7．在平面直角坐标系中，双曲线的离心率为，则实数的值xOy 2211x y m -=+2m 是▲8．在三棱锥中，直线平面，，的面积为3，若点为的重心，则S ABC -SA ⊥ABC 1SA =ABC ∆G ABC ∆三棱锥的体积为▲．S AGB -9．已知，，，则▲．1130,15n n θθθ+=︒=+︒1sin n n a θ+=N*n ∈224a a +=10．在平面直角坐标系中，若圆与曲线有2个公共点，则实数的值xOy 2220x y x ay +-+=220x y -=a 是▲．11．已知定义在区间的函数满足，当时，，则不等式[2,2]-()f x 1(2)()2f x f x +=20x -≤<2()f x x x =-的解集为▲ ．()f x x ≤12．已知函数，其中，且，若方程恰有两11()1,()(())k k f x x f x f f x +=-=N k *∈6k ≤()ln 0k f x x -=个不相等的实数根，则的取值集合为▲．k （第4题）13.在中，点，分别在线段，上，，若相交于点，且ABC ∆D E AC BC ⋅=⋅,AE BD F，则▲ ．3=⋅14. 在中，角的对边分别为，若，ABC ∆,,A B C ,,a b c 2sin sin C B A =+3sin bB a=则实数的最小值是m ▲ ．二、解答题（本大题共6小题，共90分．解答应写出文字说明、证明过程或演算步骤．）15．（本题满分14分）在中,已知角的对边分别为.ABC ∆,,A B C ,,a b c 且满足.sin(sin(sin()333b Cc B a A πππ+-+=+（1）若，求；b c =A（2）若，的值.3A π=a =sin()B C -16．（本题满分14分）已知三棱锥中，，.P ABC -AB AC ⊥AB PC ⊥（1）求证：平面；AB ⊥PAC （2）若平面分别与棱、、、相交于点、、、，αPA PB BC AC E F G H 且平面， 求证：.//PC α//EH FG17．（本题满分14分）如图，建筑公司受某单位委托，拟新建两栋办公楼，（为楼间距），两AB CD AC 楼的楼高分别为，，其中．由于委托单位的特殊工作性质，要求配电房设在的中点m a m b b a >AC 处，且满足两个设计要求：① ，②楼间距与两楼的楼高之和的比． M 90BMD ∠=︒(0.8,1)λ∈（１）求楼间距（结果用表示）；AC ,a b （２）若，是否能满足委托单位的设计要求？45CBD ∠=︒18．（本题满分16分）已知椭圆，一条准线方程为．过点:C 22221(0)x y a b a b +=>>2x =且不与轴垂直的直线与椭圆相交于两点．线段的中点为，点为轴上一点，(0,2)P y l C ,A B AB D Q y 且满足．QA QB =（1）求椭圆的方程；C （2）求证：线段的中点在定直线上；QD （3）若为等边三角形，求直线的方程．ABQ ∆l19．（本题满分16分）已知函数，．()xf x xe ax =-R a ∈(1)当时，求的最小值；0a =()f x （2）若时，恒成立，求实数的取值范围；0x ≥2()f x ax ≥a （3）若函数存在极小值，求实数的取值范围．()f x a20．（本题满分16分）已知数列的前项和为．数列满足，．}{n a n n S }{n b 21n n n S b b ++=N*n ∈（1）若，且，求正整数的值；2n n b =8m S =m （2）若数列，均是等差数列，证明：；}{n a }{n b 10b ≥（3）若数列是等比数列，公比为，且，是否存在正整数，使，，成等}{n a q 111a q b ->>≥k 1b 341k b +k b 差数列，若存在，求出一个的值，若不存在，请说明理由．k 2018届高三第四次模拟考试数学试题（附加题）21.（［选做题］请考生在A 、B 、C 、D 四小题中任选两题作答，如果多做，则按所做的前两题记分．A ．（本小题满分10分，几何证明选讲）如图，已知是的角平分线，圆过且与相切与点，圆分别与相交AD ABC ∆O ,A D BC D O ,AB AC 于. 求证：.,E F AE CF AF BE ⋅=⋅B ．（本小题满分10分，矩阵与变换）已知矩阵，在平面直角坐标系中，直线在矩阵对应的变换下得到直线111A a ⎡⎤=⎢⎥⎣⎦xOy :30l x y ++=1A -，求实数，的值．:10l x by '++=a b C ．（本小题满分10分，坐标系与参数方程选讲） 己知在平面直角坐标系中，曲线的参数方程为（为参数）．以原点为极点，以xOy C 2cos sin x y αα=⎧⎨=⎩αO 轴的非负半轴为极轴的极坐标系中，直线的极坐标方程为，直线与曲线相交x l (sin cos )2ρθθ+=l C 于两点，求线段的值．,A B ABD ．（本小题满分10分，不等式选讲） 已知正实数满足，求的最小值．,,x y z 1111x y z ++=22x yz ++22．【必做题】（本题满分10分）如图，在三棱锥中，平面，，，，P ABC -PA ⊥ABC 90BAC ∠=︒2AB =1AC =（），点，分别为，的中点．AP t =0t >D E AB PC (1)若异面直线与所成角为，求的值；AE CD 60︒t (2)记平面与平面所成的锐二面角为，证明：．PDC PBC θ(0,30)θ∈︒︒23. 【必做题】（本题满分10分）已知数列的前项和为，．}{n a n n S 01n a <<（１）若，求证：必可以被分为１组或２组，使得每组所有数的和小于；332S <123,,a a a 1（２）若，求证：必可以被分为组（），使得每组所有数的和小于．12n k S +<12,,,n a a a L m 1m k ≤≤12018届高三第四次模拟考试高三数学参考答案一、填空题1．23．4． 5．{1,2}44356． 7． 8．9．10．432313742±11．12．13.[1,2]2,4,6{}3+解：由正弦定理，，2c b =+∴，（当且仅当时取等222221324cos 22a b a b cCabab ++-===≥a 号） ∴0sin C<≤∴12)2)sin m C===+≥+，（当且仅当时取等号），∴实数．m ≥a m +意图：解三角形背景下两次使用基本不等式．二、解答题15.解：（1）∵ ，∴， b c =B C =∴，sin(sin(33b Cc B ππ+=+∵，sin(sin()sin(333b Cc B a A πππ+-+=+∴，即， …………5分sin()03a A π+=sin(03A π+=∵，∴，(0,)A π∈4333A πππ+∈（，）∴，解得. (7)分3A ππ+=23A π=（2）∵ ，3A π=∴，2sin()sin(33b B c B ππ--+=在中，由正弦定理：，………10分ABC∆sin sin(sin sin()33B C C B A ππ+-+=即，113sin (sin )sin (sin )224B C C C B B -=化简后得：. (14)分sin()B C -=16.证明：（1）∵，.AB AC ⊥AB PC ⊥又平面，平面，AC ⊂PAC PC ⊂PAC ， ………………5分AC PC C = ∴平面.AB ⊥PAC （2）∵平面，平面平面，平面//PC αPAC αEH =PC ⊂PAC ∴，………………10分//PC EH 同理，//PC FG 所以.………………14分//EH FG 17.解：（1）解：（1）∵在中，，ABM ∆2tan 2a aBMA c c ∠==在中，，CDM ∆2tan 2b bDMC c c ∠==∵，∴，∴，即，90BMD ∠=︒90BMA DMC ∠+∠=︒tan tan 1BMA DMC ∠⋅∠=24c ab =∴．………5分c =（2）在中，过点作的垂线，垂足为，CBD ∆B CD E ∴，，tan a CBE c ∠=tan b a DBE c-∠=∴tan tan tan tan()1tan tan CBE DBECBD CBE DBE CBE DBE∠+∠∠=∠+∠=-∠⋅∠，………8分221a b a bc c c a b a a c ab c c-+==-+--⋅∵，∴，………10分tan tan 451CBD ∠=︒=22a c ab bc +-=设（），由（1）可得，2b k a =1k >2c ka =∴，即，222223242a k a k a k a +-=322310k k --=设，，32()231f k k k =--1k >∴，∴函数单调递增，2()666(1)0f k k k k k '=-=->()f k 又∵，，70f =<100f =>，k <<1k k<+<∴，∴，………13分22211c k a b k k kλ===∈+++(0.8,1)λ∈∴能满足委托单位的设计要求．答：(1)楼间距为;(2)能满足委托单位的设计要求． ………………14分AC 说明：本题改编自必修4的一道例题：如图，两座建筑物AB ，CD 的底部都在同一个水平面上，且均与水平面垂直，它们的高度分别是9m 和15m ，从建筑物AB 的顶部A 看建筑物CD 的视角，45CAD ∠= 求建筑物AB ，CD 的底部之间的距离BD 。

兴化市一中2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 集合A={x|﹣1≤x ≤2}，B={x|x ＜1}，则A ∩B=（）A ．{x|x ＜1}B ．{x|﹣1≤x ≤2}C ．{x|﹣1≤x ≤1}D ．{x|﹣1≤x ＜1}2． 冶炼某种金属可以用旧设备和改造后的新设备，为了检验用这两种设备生产的产品中所含杂质的关系，调查结果如下表所示．杂质高杂质低旧设备37121新设备22202根据以上数据，则（）A ．含杂质的高低与设备改造有关B ．含杂质的高低与设备改造无关C ．设备是否改造决定含杂质的高低D ．以上答案都不对3． 3名医生和6名护士被分配到3所学校为学生体检，每校分配1名医生和2名护士．不同的分配方法共有（）A ．90种B ．180种C ．270种D ．540种4． 在△ABC 中，若a=2bcosC ，则△ABC 一定是（）A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等边三角形5． 某三棱锥的三视图如图所示，该三棱锥的表面积是 A 、 B 、28+30+C 、D 、56+60+6． 一个骰子由六个数字组成，请你根据图中三种状态所显示的数字，推出“”处的数字是（ ）1~6A ．6B ．3C ．1D ．27． 已知集合A={0，1，2}，则集合B={x ﹣y|x ∈A ，y ∈A}中元素的个数是（ ）A ．1B ．3C ．5D ．98． 若()f x 是定义在(),-∞+∞上的偶函数，[)()1212,0,x x x x ∀∈+∞≠，有()()21210f x f x x x -<-，则（）A ．()()()213f f f -<<B ．()()()123f f f <-<C ．()()()312f f f <<D ．()()()321f f f <-<班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________9． 两个随机变量x ，y 的取值表为x 0134y2.24.34.86.7若x ，y 具有线性相关关系，且＝bx ＋2.6，则下列四个结论错误的是（）y ^A ．x 与y 是正相关B ．当y 的估计值为8.3时，x ＝6C ．随机误差e 的均值为0D ．样本点（3，4.8）的残差为0.6510．下列命题中的说法正确的是（）A ．命题“若x 2=1，则x=1”的否命题为“若x 2=1，则x ≠1”B ．“x=﹣1”是“x 2+5x ﹣6=0”的必要不充分条件C ．命题“∃x ∈R ，使得x 2+x+1＜0”的否定是：“∀x ∈R ，均有x 2+x+1＞0”D ．命题“在△ABC 中，若A ＞B ，则sinA ＞sinB ”的逆否命题为真命题11．一个正方体的顶点都在球面上，它的棱长为2cm ，则球的表面积是（ ）A ．8πcm 2B ．12πcm 2C ．16πcm 2D ．20πcm 212．i 是虚数单位，计算i+i 2+i 3=（）A ．﹣1B ．1C ．﹣iD ．i二、填空题13．将全体正整数排成一个三角形数阵：按照以上排列的规律，第n 行（n ≥3）从左向右的第3个数为 ．14．已知函数f （x ）=，若f （f （0））=4a ，则实数a= ．15．在△ABC 中，点D 在边AB 上，CD ⊥BC ，AC=5，CD=5，BD=2AD ，则AD 的长为 ．　16．设为单位向量，①若为平面内的某个向量，则=||•；②若与平行，则=||•；③若与平行且||=1，则=．上述命题中，假命题个数是 ．　17．等比数列{a n }的前n 项和S n ＝k 1＋k 2·2n （k 1，k 2为常数），且a 2，a 3，a 4－2成等差数列，则a n ＝________．18．如图，在三棱锥中，，，，为等边三角形，则P ABC -PA PB PC ==PA PB ⊥PA PC ⊥PBC △PC 与平面所成角的正弦值为______________.ABC【命题意图】本题考查空间直线与平面所成角的概念与计算方法，意在考查学生空间想象能力和计算能力．三、解答题19．（本小题满分12分）如图，在直二面角中，四边形是矩形，，，是以为直角顶C AB E --ABEF 2=AB 32=AF ABC ∆A 点的等腰直角三角形，点是线段上的一点，．P BF 3=PF （1）证明：面；⊥FB PAC （2）求异面直线与所成角的余弦值．PC AB 20．已知在△ABC 中，A （2，4），B （﹣1，﹣2），C （4，3），BC 边上的高为AD ．（1）求证：AB ⊥AC ； （2）求向量．21．如图，在四棱锥P ﹣ABCD 中，AD ∥BC ，AB ⊥AD ，AB ⊥PA ，BC=2AB=2AD=4BE ，平面PAB ⊥平面ABCD ，（Ⅰ）求证：平面PED ⊥平面PAC ；PCABEF（Ⅱ）若直线PE 与平面PAC 所成的角的正弦值为，求二面角A ﹣PC ﹣D 的平面角的余弦值．22．（本小题满分13分）设，数列满足：，．1()1f x x =+{}n a 112a =1(),n n a f a n N *+=∈（Ⅰ）若为方程的两个不相等的实根，证明：数列为等比数列；12,λλ()f x x =12n n a a λλ⎧⎫-⎨⎬-⎩⎭（Ⅱ）证明：存在实数，使得对，．m n N *∀∈2121222n n n n a a m a a -++<<<< ）23．已知y=f （x ）的定义域为[1，4]，f （1）=2，f （2）=3．当x ∈[1，2]时，f （x ）的图象为线段；当x ∈[2，4]时，f （x ）的图象为二次函数图象的一部分，且顶点为（3，1）．（1）求f （x ）的解析式；（2）求f （x ）的值域．24．（本小题满分12分）已知．1()2ln ()f x x a x a R x=--∈（Ⅰ）当时，求的单调区间；3a =()f x （Ⅱ）设，且有两个极值点，其中，求的最小值．()()2ln g x f x x a x =-+()g x 1[0,1]x ∈12()()g x g x -【命题意图】本题考查导数的应用等基础知识，意在考查转化与化归思想和综合分析问题、解决问题的能力．兴化市一中2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题题号12345678910答案D A D B B A C D D 题号1112答案B A二、填空题13．　3+　．14．　2　．15．　5　．16．　3　．17．18三、解答题19．20．21．22．23．24．。

兴化市第一中学2018春学期期初检测高三数学一、填空题：（每小题5分）1．已知集合{}0,1,2A =，集合11,B x ⎧⎫=⎨⎬⎩⎭，且B A ⊆，则实数x = ▲ .2．已知复数31i z i-=+（i 是虚数单位），则z 的实部是 ▲ ． 3．根据如图所示伪代码，当输入的a 的值为3时，最后输出的S 的值为 ▲ .4．某校有足球、篮球、排球三个兴趣小组，共有成员120人，其中足球、篮球、排球的成员分别有40人、60人、20人．现用分层抽样的方法从这三个兴趣小组中抽取24人来调查 活动开展情况，则在足球兴趣小组中应抽取 ▲ 人．5．已知实数x ，y 满足⎪⎩⎪⎨⎧≤+≤+>y x y x x 2270，则x y 的最小值是 ▲ . 6．“0=a 错误！未找到引用源。

” 是“函数)()(23R x ax x x f ∈+=错误！未找到引用源。

为奇函数”的 ▲ 条件.7．在平面直角坐标系xOy 中，双曲线2221x y a-=与抛物线212y x =-有相同的焦点，则双曲线的两条渐近线的方程为 ▲ .8．设n S 是等比数列{}n a 的前n 项的和，若3620a a +=，则36S S 的值是 ▲ ． 9．从甲、乙、丙、丁4名学生中随机选出2人，则甲被选中的概率为 ▲ .10．已知单位向量a ， b 的夹角为120︒，那么2a xb - （x R ∈）的最小值是 ▲ ．11．已知锐角α的终边上一点()1cos80,sin80P +︒︒，则锐角α= ▲ ．12．一个封闭的正三棱柱容器，高为3，内装水若干(如图甲，底面处于水平状态)，将容器放倒(如图乙，一个侧面处于水平状态)，这时水面与各棱交点E ， F ， 1F ， 1E 分别为所在棱的中点，则图甲中水面的高度为 ▲.13．已知函数()3f x x =．设曲线()y f x =在点()()11P x f x ，处的切线与该曲线交于另一点()()22Q x f x ，，记()f x '为函数()f x 的导数，则()()12f x f x ''的值为 ▲ ． 14．已知函数()322f x x x a =--，若存在(]0,x a ∈-∞，使()00f x ≥，则实数a 的取值范围是 ▲ ．二、解答题：15. （本小题14分）如图，在正三棱柱111ABC A B C -中，已知D ，E 分别为BC ，11B C 的中点，点F 在棱1CC 上，且1EF C D ⊥．求证：（1）直线1A E ∥平面1ADC ；（2）直线EF ⊥平面1ADC ．16．（本小题14分）已知锐角ABC ∆中的三个内角分别为,,A B C ．（1）设⋅=⋅，判断ABC ∆的形状；（2）设向量(22sin ,,cos 2,2cos 12C s C t C ⎛⎫==- ⎪⎝⎭，且//s t ，若1sin 3A =，求sin 3B π⎛⎫- ⎪⎝⎭的值．。