9.5 解直角三角形的应用课件(青岛版八年级下册) (2)

‹# ›
青岛
• 在Rt△ABC 中,∠C=900 ,AC=4, 3 求AB、BC的值 sinA = 5
• 解： 3 BC ∵ sinA = 5 = AB ∴ 设BC=3k，则
AB=5k，根据勾股 定理可得AC=4k
B
∵ AC=4k=4 ∴ k=1 ∴ AB=5，BC=3
A
4
C
‹# ›
青岛
-- 青岛版
‹# ›
青岛
‹# ›
青岛
如下图所示,假设BC＝a,则
AB＝2a ,AC＝ 3a
2a
60°
B
a
┌
A
30°
3a
BC AB
C
sin30°＝ a 1 ＝ 2a＝ 2 cos30°＝ AC 3a 3 ＝2 AB ＝ 2a tan30°＝ a BC 3 ＝ 3a ＝ 3 AC
‹# ›
青岛
做一做 • ⑴60°角的三角函数值分别是多少? 你是怎样得到的? • ⑵45°角的三角函数值分别是多少? 你市怎样得到的? • ⑶完成下表:
‹# ›
青岛
9.2 30°45°60°角的三角函数值
‹# ›
青岛
复习: 在Rt△ABC中,如果锐角A确定,那么∠A 的对边与斜边的比、邻边与斜边比、 对边与邻边的比也随之确定,分别叫做 ∠A的正弦、余弦、正切. B
c
a
┌
sinA=cosB
A
C
,
a sinA＝ c
,
b cosA＝ c
b
a tanA＝ b
∠A的
∠A的
‹# ›
青岛
B
B１
已经证得△ABC∽△AB1C1 ①可得
AC AB = AC1 AB1

解：如图，α = 30° ， β= 60°，AD＝120． ∵ , ∴BD=AD·tanα=120×tan30︒, =120× =40 . CD=AD·tanβ=120×tan60︒, =120× =120 . ∴BC=BD+CD=40 +120 =160 ≈277(m).答：这栋楼高约为277m.
例1 如图，小明在距旗杆4.5 m的点D处，仰视旗杆顶端A，仰角（∠AOC）为50°；俯视旗杆底部B，俯角（∠BOC）为18°.求旗杆的高.(结果精确到0.1 m)
例题示范
知识点2 方向角方位角：由正南或正北方向线与目标方向线构成的锐角叫做方位角．如下图中的目标方向OA,OB,OC,OD的方向角分别表示________60°，________45°(或__________)，_________80°及_________30°.
拓展提升
1.热气球的探测器显示，从热气球看一栋楼顶部的仰角为30°，看这栋楼底部的俯角为60°，热气球与楼的水平距离为120 m，这栋楼有多高(结果取整数)？
分析：如图，α=30°，β=60°.在Rt△ABD中，α =30°，AD＝120，所以利用解直角三角形的知识求出BD；类似地可以求出CD，进而求出BC．
第二十六章 解直角三角形
26.4 解直角三角形的应用
第1课时 仰角、俯角、方位角问题
学习目标
学习重难点
重点
难点
1.巩固解直角三角形有关知识，了解仰角、俯角、方向角的概念.2.运用解直角三角形知识解决与仰角、俯角和方位角有关的实际问题.
运用解直角三角形知识解决与仰角、俯角和方位角有关的实际问题.
将某些实际问题中的数量关系，归结为直角三角形中元素之间的关系，从而解决问题.
回顾复习

课前复习
二次函数有哪几种表达式 ?
• 一般式：y =ax2 +bx +c • (顶a≠点0)式：y =a(x -h)2 +k (a≠0)
• 交点式：y =a(x -x1)(x -x2) (a≠0)
例题选讲
例 1 抛物线的顶点为〔－1 ,－6〕 ,与轴交点为
〔2 ,3〕求抛物线的〔－1 ,－6〕 ,
并经过点M（0,1），求抛物线的表达式？
解： 因为函数过A〔－1 ,0〕 ,B〔1,0〕两点 ： 所以设所求的二次函数为y =a(x＋1)(x－1y〕
由条件得： 点M( 0,1 )在抛物线上
x o
所以：a(0 +1)(0 -1) =1
得： a = -1
故所求的抛物线表达式为 y = - (x＋ 1即)：(xy -=1－) x2 +1
解： 设所求的二次函数为 y =ax2 +bx +c y
将A、B、C三点坐标代入得：
a -b +c =6
16a +4b +c =6 9a +3b +c =2
ox
解得：
a =1, b = -3,
c =2
所以：这个二次函数表达式为：
y =x2 -3x +2
封面 例题
例题选讲
例 3 已知抛物线与X轴交于A（－1，0），B（1,0）
31
跟踪训练
1. 一个钢球沿坡角31°的斜坡向上滚动了5米， 此时钢球距地面的高度是（ ）米 Ａ．5sin 31 Ｂ．5cos31 Ｃ．5 tan 31
31
2.如图所示，铁路的路基横断面是等腰梯形，斜坡
的坡度为1 : 3 ，坡面 的水平宽度为 3 3 m ，基面

教学课题
1、知识目标：
⑴懂得常见名词（如仰角、俯角）的意义
⑵能正确理解题意，将实际问题转化为数学问题
⑶能利用已有知识，通过直接解三角形或列方程的方法解决一些实际问题。
2、能力目标：培养学生分析问题和解决问题的能力，培养学生思维能力的灵活性。
3、情感目标：使学生能理论联系实际，培养学生的对立统一的观点。
(设计意图：学生思考问题，寻找解题方法。把问题抛给学生，对其养成独立思考、善于分析问题有所帮助，同时，通过实例创设问题情景，使学生感受到数学与生活的密切联系，增进对数学的理解，激发、认识仰角与俯角：
想要解决刚才的问题，我们先来了解仰角、俯角的概念，
（flash动画：/23334.htm）。
(设计意图:这里运用了动画直观演示，使学生思维从感性
认识上升到理性认识，有利于培养学生的抽象思维能力。)
（2）、引导学生小组探究解决导入中提出的问题。为了
测量东方明珠塔的高度，同学们在距离东方明珠塔200米处
的地面上，用高1.20米的测角仪测得东方明珠塔顶的仰角
为60°48′．根据测量的结果，小亮画了一张示意图（用
整个教学过程主要分四部分：第一部分是考点整合——复习简单的解直角三角形，直角三角形得边角关系，解直角三角形得类型，解直角三角形得应用；第二部分是归类示例——通过三个类型三个例题讲解解直角三角形的应用；第三部分是课时小结———总结应用解直角三角形的方法解决实际问题的一般步骤；第四部分是课时作业———巩固本节所学。
3、巩固训练
练习1．如图，在电线杆上离地面6米处用拉线固定电线杆，拉线和地面之间的夹角为60°,求拉线AC的长和拉线下端点A与线杆底部D的距离（精确到0 .1米）.
（设计意图：使学生巩固利用直角三角形的有关知识解决实际问题，考察建立数学模型的能力，转化的数学思想在学习中的应用，提高学生分析问题、解决问题的能力。以及在学习中还存在哪些问题，及时反馈矫正。）

八年级数学下册 9.5解直角三角形的应用导学案青岛版9、5解直角三角形的应用（2）课本内容：79页----80页课前准备：刻度尺三角尺一副计算器学习目标：1、将实际问题中的数量关系归结为直角三角形中元素之间的关系。

2、熟知建立和求解数学模型的过程。

一、自主预习：课本79页例3 独立完成第一问题与小组同学交流（课前完成）批注(1)画出示意图并计算在课堂上学生展示预习结果。

二、预习课本79页例3第二个问题，完成下列问题1、通过把实物图抽象为几何图形，画出示意图2、根据数据EF=20米∠AEF=35 ，计算出EF的长度，再说明AF与CE的关系，ED与FB的关系，计算出ED的长度。

根据ED的长度说明北楼一楼被影响采光的高度。

A C FEBD3、熟知对解决实际问题的基本思路概括示意图。

三、巩固练习：1、例3第二问题能否根据南楼高度16、8米，太阳光线与地面的夹角35计算南楼影子是否影响北楼一楼的采光。

批注(2)小组交流达成共识，某小组展示，形成明确答案。

2、在某广场上空飘着一只气球P，A、 B 是地面上相距90米的两点，他们分别在气球的正西和正东，测得仰角∠PAB=30，求气球P的高度。

P BH四、达标检测：1、课外活动小组测量学校旗杆的高度如图，当太阳光线与地面35时，测的旗杆AB在地面的投影BC长为23、5米，则旗杆AB的高度是（）米。

（精确到0、1米）。

A CB3、汶川地震后抢险队派一架直升机去A 、B两个村庄抢险，飞机在距地面450米上空的P点测得A 的俯角为30，测得B的俯角为60，求A、B两个村转的距离。

30QP60ACB五、课后提升1、小明要测量河内小岛B到公路C的距离，在A点测的∠BAD=30゜,在C点测得∠BCD=60゜又测得AC=50米，则小岛B到公路的距离为（）米。

B ACD3、为了测量河流某一段的宽度，在河的北岸选了点A，在河的南岸选取了相距200m的B,C两点，分别测得∠ABC=60゜,∠ACD=45゜球这段河的宽度AD的长。

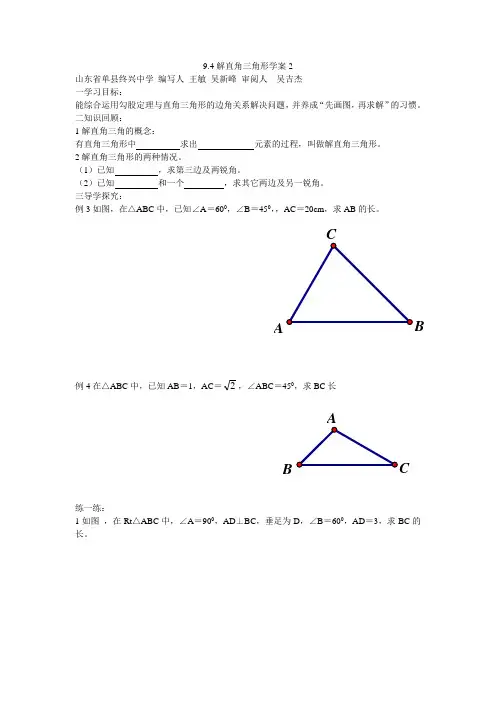
9.4解直角三角形学案2山东省单县终兴中学编写人王敏吴新峰审阅人吴吉杰一学习目标：能综合运用勾股定理与直角三角形的边角关系解决问题，并养成“先画图，再求解”的习惯。

二知识回顾：1解直角三角的概念：有直角三角形中求出元素的过程，叫做解直角三角形。

2解直角三角形的两种情况。

（1）已知，求第三边及两锐角。

（2）已知和一个，求其它两边及另一锐角。

三导学探究：例3如图，在△ABC中，已知∠A＝600，∠B＝450，，AC＝20cm，求AB的长。

A B 例4在△ABC中，已知AB＝1，AC＝2，∠ABC＝450，求BC长B练一练：1如图，在Rt△ABC中，∠A＝900，AD⊥BC，垂足为D，∠B＝600，AD＝3，求BC的长。

BC2在等腰三角形ABC 中，AB ＝AC ，且一腰长于底边长的比 是5︰8，求sinB.cosB 的值。

当堂达标：1在△ABC 中，∠B ＝450，cosC ＝53，AC ＝5a ，则△ABC 的面积用含a 的式子表示 是B2 如图，在△ABC 中，AB ＝5，AC ＝7，∠B ＝600，求BC 长BC3如图在△ABC 中，AD 是BC 边上的高，tanB ＝cos ∠DAC ， （1） AC 与BD 相等吗？为什么？ （2） 若sinC ＝1312，BC ＝12，求AD 长 ＋B4 △ABC 中,已知∠B ＝450，∠C ＝600，BC ＝53＋5，求AB 和AC 长5 已知如图，在△ABC 中，AB ＝20，AC ＝30，∠A ＝1500，求△ABC 的面积C六能力提升：1 在Rt△ABC中，∠C＝900，CD⊥AB，垂足为D，AB＝6，AD＝2，求sinA，cosA，tanA 的值，2如图，在△ABC中，∠ACB＝1180，BC＝4，求AC边上的高A。

角函数求解
计算角度证结果：检 查计算结果是 否满足三角形 内角和为180
度的条件
添加标题
确定已知条件：已知三角形的边长和角度
添加标题
利用正弦定理：sin/ = sinB/b = sinC/c
添加标题
利用余弦定理：cos = (b^2 + c^2 - ^2) / (2bc)
正弦定理：在直角三角形中 任意一边的长度等于其对角 的正弦值乘以斜边的长度
余弦定理：在直角三角形中 任意两边长度的平方和等于 斜边的平方
正切定理：在直角三角形中 任意一边的长度等于其对角 的正切值乘以斜边的长度
余切定理：在直角三角形中 任意两边长度的平方差等于 斜边的平方
正割定理：在直角三角形中 任意一边的长度等于其对角 的正割值乘以斜边的长度
确保测量工具的 准确性和稳定性
避免在危险区域 进行测量如高空、
高压电等
遵守操作规程确 保人身安全
做好防护措施如 佩戴安全帽、手
套等
及时清理现场避 免杂物影响测量
结果
遇到突发情况及 时停止操作并寻
求帮助
仰角和俯角为0度：此时三角形退化为直线无法求解
仰角和俯角为90度：此时三角形退化为直角三角形可以直接求解
全站仪等
测量误差：注 意测量误差对 仰角和俯角测 量结果的影响
测量环境：注 意测量环境的 影响如温度、 湿度、风速等
测量方法：注 意测量方法的 选择如直接测 量、间接测量
等
测量误差：测量工具的精度、测量人员的操作水平等
计算误差：计算过程中的舍入误差、公式使用错误等
环境误差：温度、湿度、光照等环境因素对测量结果的影响
添加文档副标题
目录
01.
02.

1.(2010.潍坊)路边路灯的灯柱垂直于地面，灯杆 的长为2米，灯杆与灯柱成角，锥形灯罩的轴线 与灯杆垂直，且灯罩轴线正好通过道路路面的中 心线（在中心线上）.已知点与点之间的距离为 12米，求灯柱的高.（结果保留根号）
2.（2011•潍坊）今年“五一“假期．某数学活动小组组织一次登 山活动．他们从山脚下A点出发沿斜坡AB到达B点．再从B点沿 斜坡BC到达山顶C点，路线如图所示．斜坡AB的长为1040米， 斜坡BC的长为400米，在C点测得B点的俯角为30°．已知A点海 拔121米．C点海拔721米。（1）求B点的海拔（2）求斜坡AB的 坡度．
1. 如图，从热气球C上测定建筑物A、B底部的俯角分别为30° 和60°，如果这时气球的高度CD为150米，且点A、D、B在同 一直线上，建筑物A、B之间的距离为（ ）
A.150 3 米 B.180 3 米 C.200 3 米 D.220 3 米
2. 山顶上有一旗杆，在地面上一点A处测 得杆顶B的俯角α =600，杆底C的俯角β =450，已知旗杆高BC=20米，求山高 CD。
解： 因为函数过A（－1，0），B（1,0）两点 ： 所以设所求的二次函数为y=a(x＋1)(x－1）y
由条件得： 点M( 0,1 )在抛物线上
x o
所以：a(0+1)(0-1)=1
得： a=-1 故所求的抛物线表达式为 y=- (x＋
1即)：(xy-=1－) x2+1
封面 例题
小组探究
1、已知二次函数对称轴为x=2，且过（3，2）、 （-1,10）两点，求二次函数的表达式。
根据题意可知
抛物线经过(0，0)，(20，16)和(40，0)三点
可得方程组
评价 通过利用给定的条件

眺望大厦，并测得大厦顶部的仰角为45°，而大厦底
部的俯角为30°。求该大厦的高度。
B
A
┏
D
C
有关实际问题 问题答案
--------------
解直角三角形的问题 求出有关的边或角
如图，有两棵树，一棵树高8米，另一棵树 高2米，两树相距8米，一只小鸟从一棵树 的树梢飞到另一棵树的树梢，至少飞了 __1_0____米。
8米
2米
8米
例1、住宅小区楼房之间的距离是建楼和购房 时人们所关心的问题之一。如图，住宅小区 南、北两栋楼房的高度均为16.8米。已知当 地冬至这天中午12时太阳光线与地面所成的 角是35°。 （1）要使这时南楼的影子恰好落在北楼的 墙角，两楼之间的距离应为多少米？（精确
到0.1米）
AБайду номын сангаас
C
16.8
35°
？
16.8米
B
解：（1）如图，南楼为AB，北楼为
35°
?
D
CD,AB⊥BD,CD⊥BD,垂足为B、D，
AD为冬至这天12时的太阳光线，BD为影子.
在Rt△ABD中，已知AB=16.8米，∠ADB=35°， ∵tan∠ADB= AB ， ∴BD= 16.8 ≈B2D4.0(米） 即两楼之tan间35的 距离为24.0米
1、如图：在Rt△ABC中，
B
说出角与角、边与边、 c
角与边之间的关系？
a
┏
(1)三边之间的关系:
A
bC
a2＋b2＝c2（勾股定理）；
(2)两锐角之间的关系:
∠ A＋ ∠ B＝ 90º；
(3)边角之间的关系:
a
sinA=
,cosA= b , tanA=

选择合适的解法
根据实际情况选择合适的解法，如近似计算、 精确计算等。
注意单位统一
在实际应用中，要注意单位统一，避免计算 错误。
考虑多解情况
在某些情况下，解直角三角形可能存在多个 解，需要全面考虑。
06
练习与巩固
基础练习题
总结词
掌握基本概念和公式
直角三角形中的角度和边长关系
理解直角三角形中锐角、直角和钝角之间 的关系，以及边长与角度之间的勾股定理 。
利用三角函数定义求解
总结词
通过已知角度和邻边长度，求对边或 斜边长度。
详细描述
根据三角函数定义，已知一个锐角和它 所对的边，可以通过三角函数求出其他 两边。例如，已知∠A=30°和a=1，可 以通过三角函数sin(30°)求出对边b。
利用勾股定理求解
总结词
通过已知两边的长度，求第三边长度。
详细描述
向。
确定建筑物的角度
在建筑设计中，通过解直角三角形， 可以确定建筑物的角度和方向。
确定建筑物的长度
在建筑设计中，通过解直角三角形， 可以确定建筑物的长度和方向。
物理问题中的运用
确定物体的运动轨迹
在物理问题中，通过解直角三角形，可以确定物体的运动轨 迹和方向。
确定物体的受力情况
在物理问题中，通过解直角三角形，可以确定物体的受力情 况和方向。
04
实际应用案例
测高问题
01
02
03
测量山的高度
通过测量山脚和山顶的仰 角，利用解直角三角形的 知识，可以计算出山的高 度。
测量楼的高度
利用解直角三角形的知识， 通过测量楼底和楼顶的仰 角，可以计算出楼的高度。
测量树的高度
通过测量树底部和树顶部 的仰角，利用解直角三角 形的知识，可以计算出树 的高度。

解直角三角形的方法
1
已知一边和一角求其他边
2
利用正弦、余弦或正切定理。Байду номын сангаас
3
已知两边求第三边
利用勾股定理或正弦定理。
已知两角求第三角及其他边
根据直角三角形内角和为180度可求。
结论和总结
结论
直角三角形是应用数学中最基础的模型，在 实际生活中有着广泛的应用。
总结
通过本次课件的学习，我们了解了直角三角 形的定义、特征和性质、三边关系、角度关 系以及如何应用它们解决实际问题，掌握了 解直角三角形的方法。
性质
勾股定理、正弦定理、余弦定理、正切定理都是 针对直角三角形的定理。
直角三角形的三边关系
勾股定理
直角边的平方和等于斜边的平方。
正弦定理
任意一角的正弦值与其所对的边成比例，即a/sinA=b/sinB=c/sinC。
余弦定理
直角三角形的斜边平方等于两直角边平方之和，即c²=a²+b²。
直角三角形的角度关系
1
45-45-90三角形
等腰直角三角形的两个锐角相等，都
30-60-90三角形
2
是45度。
等腰直角三角形的两个锐角不等，大
角为60度，小角为30度。
3
其他角度关系
直角三角形内角和为180度。
应用直角三角形的实际问题
航海中的应用
直角三角形可用来测量离岸估计距离、速度和位 置。
武器轨迹的应用
弹道计算需要用到直角三角形的三角函数。
解直角三角形
在本次课件中，我们将学习直角三角形的定义、特征、性质、三边关系、角 度关系以及如何应用直角三角形解决实际问题。
直角三角形的定义

第二十六章 解直角三角形
26.4 解直角三角形的应用
第2课时 坡度、坡角问题
学习目标
学习重难点
重点
难点
1..加强对坡度、坡角、坡面概念的理解和认识，了解坡度与坡面陡峭程度间的关系.2.能把一些较复杂的图形转化为解直角三角形的问题.3.能解决堤坝等关于斜坡的实际问题，提高解决实际问题的能力.
第3题图
第4题图
B
A
5．水库拦水坝的横断面是四边形ABCD，AD∥BC，背水坡CD的坡比i＝1∶1，已知背水坡的坡长CD＝24 m，则背水坡的坡角α为____，拦水坝的高度为_______ m.6．如图，在坡比为i＝1∶2的山坡上种树，要求株距(相邻两树间的水平距离)是6米，斜坡上相邻两树间的坡面距离是______米．
创设情境
如图，从山脚到山顶有两条路AB与BC，问哪条路比较陡？
新知引入
如图，在筑坝、开渠、挖河和修路时，设计图纸上都要注明斜坡的倾斜程度.我们通常把坡面的垂直高度h和水平宽度l的比叫做坡面的坡度（或坡比），坡面与水平面的夹角α叫做坡角.显然，tanα=.
知识点 坡度、坡角
例题示范
第1题图
第2题图
B
C
3.如图，先锋村准备在坡角为α的山坡上栽树，要求相邻两树之间的水平距离为5米，那么这两树在坡面上的距离AB为( )A. 米 B. 米 C.5sinα 米 D. 米4.小明想测量一棵树的高度，他发现树的影子恰好落在地面和一斜坡上．如图，此时测得地面上的影长为8米，坡面上的影长为4米．已知斜坡的坡角为30°，同一时刻，一根长为1米、垂直于地面放置的标杆在地面上的影长为2米，则树的高度为( )A. 米 B.12米 C. 米 D.10米
坡度、坡角、坡面的概念，了解坡度与坡面陡峭程度间的关系.

八年级数学下册 9.4 解直角三角形（2）导学案青岛版9、4 解直角三角形课本内容：P74-P75课前准备：三角板学习目标：1、通过解直角三角形提高学生的分析解决问题能力。

2、通过构建直角三角形并解直角三角形，感受数形结合的作用。

一、完成下列各题。

小组内讨论1、RtABC中，∠C=90, CD⊥AB于D, AD=3, ∠B=60,求AB,BC【1】批注【1】XXXXX：让学生了解已知元素和需求元素所在三角形，数形结合能力 C B D A2 △ABC中，AB=AC, AB:BC=5:8, 求sinB, cos B、【2】批注【2】XXXXX：怎样构建直角三角形？应把已知元素和所求元素构建在同一直角三角形中。

A B C二、板书例3、△ABC中，∠A=60, ∠B=45，AC=20厘米，求AB的长。

CA B1、小组交流构建直角三角形的方法（辅助线的做法）【3】批注【3】XXXXX：小组内交流统一意见后，考虑解法，引导学生能解哪个直角三角形?需要解直角三角形?2、最后统一解题格式。

三、巩固练习【4】批注【4】XXXXX：提醒学生数形结合，利于解决问题1、等腰三角形的底边长为6，面积为3，求这个等腰三角形的顶角。

2、在△ABC中，已知∠B=30，SinC=4/5,AC=10,求AB的长。

四、达标测试1、在直角坐标系中，直线y=x上一点A,OA=52,求点A 的坐标。

Y y=x A O X2、等腰三角形，顶角120，腰长10cm,求等腰三角形的周长。

五、作业：P761、2、。

并经过点M（0,1），求抛物线的表达式？
解： 因为函数过A〔－1 ,0〕 ,B〔1,0〕两点 ： 所以设所求的二次函数为y =a(x＋1)(x－1y〕
由条件得： 点M( 0,1 )在抛物线上
x o
所以：a(0 +1)(0 -1) =1
得： a = -1
故所求的抛物线表达式为 y = - (x＋ 1即)：(xy -=1－) x2 +1
解直角三角形〔1〕
学习目标
直角三角形的两个元素〔至||少一边〕 会解直角三角形 .
知识回忆
A
在直角三角形中 ,我们把两个锐角、三条边
称为直角三角形的五个元素. 图中∠A ,∠B ,a ,b ,c即为直角三角形
b
c
的五个元素.
Ca
B
知识回忆
A
在直角三角形中 ,我们把两个锐角、三条边
称为直角三角形的五个元素. 图中∠A ,∠B ,a ,b ,c即为直角三角形
解： 设所求的二次函数为 y =ax2 +bx +c y
将A、B、C三点坐标代入得：
a -b +c =6
16a +4b +c =6 9a +3b +c =2
ox
解得：
a =1, b = -3,
c =2
所以：这个二次函数表达式为：
y =x2 -3x +2
封面 例题
例题选讲
例 3 已知抛物线与X轴交于A（－1，0），B（1,0）ຫໍສະໝຸດ 封面 例题小组探究
1、二次函数对称轴为x =2 ,且过〔3 ,2〕、〔 1,10〕两点 ,求二次函数的表达式 .
解：设y =a(x -2)2 -k
2、二次函数极值为2 ,且过〔3 ,1〕、 〔 -1,1〕两点 ,求二次函数的表达式 .

C
△ABC不是直角三角 形，怎么办？
A
B
D
转化思想：作AB边上的高，把锐角三角形转
化为直角三角形，把问题转化为
解直角三角形．
化 未知 为 已知．
跟踪练习
1.如图,在Rt△ABC中，AD⊥BC，垂
A
足为D，∠B=60°，AC=5，AD=3，
求BC的长．
B
C
D
2. 在等腰三角形ABC中，AB=AC，且一腰长与底边 的比是5:8,求sinB，cosB的值．
例题选讲
例 1 已知抛物线的顶点为（－1，－6），与轴交点为
（2，3）求抛物线的表达式？
解：因为二次函数图像的顶点坐标是（－1，－6），
所以，设所求的二次函数为 y=a(x＋1)2-6
由条件得：点( 2 , 3 )在抛物线上，
代入上式，得
3=a（2+1）2-6,
得 a=1
所以，这个抛物线表达式为 y=(x＋1)2-6 即：y=x2+2x－5
得： a=-1 故所求的抛物线表达式为 y=- (x＋
1即)：(xy-=1－) x2+1
封面 例题
小组探究
1、已知二次函数对称轴为x=2，且过（3，2）、 （-1,10）两点，求二次函数的表达式。
解：设y=a(x-2)2-k
2、已知二次函数极值为2，且过（3，1）、 （-1,1）两点，求二次函数的表达式。
求二次函数表达式的一般方法：
▪ 已知图象上三点或三对的对应值，
通常选择一般式
y
▪ 已知图象的顶点坐标、对称轴或和最值
通常选择顶点式
▪ 已知图象与x轴的两个交点的横x1、x2，
x 通常选择交点式。 o
确定二次函数的表达式时，应该根据条件的特点， 恰当地选用一种函数表达式。