[整理]SPSS分析：嵌套式两因素方差分析(单变量)-学生 王露实验数据分析.

SPSS双因素方差分析双因素方差分析是一种用于研究两个或多个自变量对因变量之间是否存在影响的统计方法。

在本文中，我们将讨论SPSS中如何进行双因素方差分析，并对其结果进行解释。

首先，我们需要首先导入我们的数据集，并确保数据集中包含我们要研究的因变量和两个自变量。

在SPSS中，我们可以通过依次点击"文件"->"导入"->"数据"来加载数据集。

一旦我们成功加载数据集，我们可以开始进行双因素方差分析。

在SPSS中，我们可以通过依次点击"分析"->"一般线性模型"->"一元方差分析"来进行。

在进行方差分析之前，我们需要将自变量添加到"因子"的列表中。

我们可以使用鼠标将自变量拖拽到"因子"列表中，或者通过点击"添加"按钮手动将其添加。

在添加完自变量后，我们可以点击"模型"选项卡，选择我们感兴趣的方差分析模型。

在双因素方差分析中，共有三种模型可供选择：主效应模型、交互作用模型和自由模型。

-主效应模型：计算每个自变量的主效应，并忽略它们之间是否存在交互作用。

-交互作用模型：计算自变量之间是否存在交互作用，并同时计算每个自变量的主效应。

-自由模型：不计算任何主效应或交互作用，仅用于比较不同模型之间的显著性。

选择适当的模型后，我们可以点击"可选"选项卡，设置其他参数，比如显著性水平、效应大小等。

一旦我们完成了所有设置，可以点击"确定"开始进行方差分析。

SPSS将会自动生成方差分析的结果报告。

在报告中，我们可以找到各个自变量的主效应、交互作用以及整体模型的显著性等信息。

一般来说，我们关注的主要结果包括：组间方差、组内方差、平方和、均方、F统计值、显著性水平等。

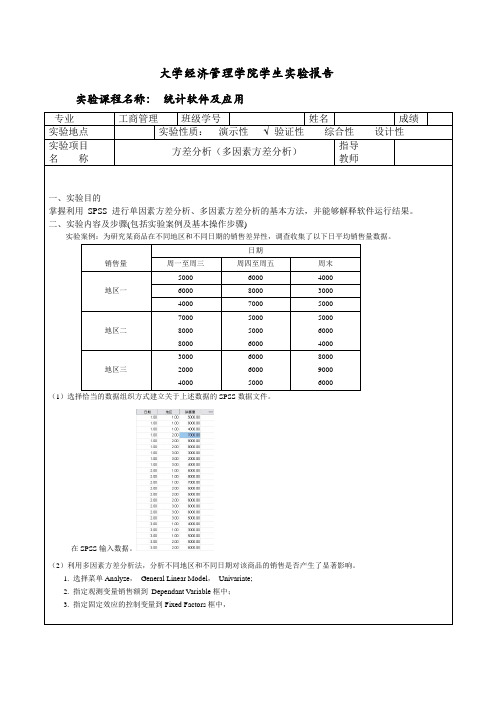
大学经济管理学院学生实验报告实验课程名称：统计软件及应用专业工商管理班级学号姓名成绩实验地点实验性质：演示性 验证性综合性设计性实验项目名称方差分析（多因素方差分析）指导教师一、实验目的掌握利用SPSS 进行单因素方差分析、多因素方差分析的基本方法，并能够解释软件运行结果。

二、实验内容及步骤(包括实验案例及基本操作步骤)实验案例：为研究某商品在不同地区和不同日期的销售差异性，调查收集了以下日平均销售量数据。

销售量日期周一至周三周四至周五周末地区一5000 6000 4000 6000 8000 3000 4000 7000 5000地区二700080008000500050006000500060004000地区三300020004000600060005000800090006000（1）选择恰当的数据组织方式建立关于上述数据的SPSS数据文件。

在SPSS输入数据。

（2）利用多因素方差分析法，分析不同地区和不同日期对该商品的销售是否产生了显著影响。

1. 选择菜单Analyze，General Linear Model，Univariate;2. 指定观测变量销售额到Dependant Variable框中；3. 指定固定效应的控制变量到Fixed Factors框中，4. OK，得到分析结果。

（3）地区和日期是否对该商品的销售产生了交互影响？若没有显著的交互影响，则试建立非饱和模型进行分析，并与饱和模型进行对比。

三、实验结论(包括SPSS输出结果及分析解释)SPSS输出的多因素方差分析的饱和模型分析：表的第一列是对观测变量总变差分解的说明；第二列是观测变量变差分解的结果；第三列是自由度；第四列是方差；第五列是F检验统计量的观测值；第六列是检验统计量的概率P-值。

F日期，，F地区，F日期*地区概率P-值分别为0.254,0.313，0.000。

如果显著性水平α为0.05，由于F日期、，F地区大于显著性水平α，所以不应拒绝原假设，不同地区和不同日期对该商品没有显著性影响。

单因素方差分析 SPSS简介SPSS（统计软件包社会科学）是一款功能强大的统计软件，广泛应用于社会科学研究领域。

在此文档中，我们将介绍如何使用SPSS进行单因素方差分析（One-way ANOVA）。

单因素方差分析单因素方差分析是一种统计方法，用于比较两个或更多个组之间的均值差异。

它的基本原理是将总体均值差异分解为组内变异和组间变异两部分。

通过比较组间变异与组内变异的大小，我们可以判断组之间是否存在显著差异。

在进行单因素方差分析之前，我们需要满足以下前提条件： 1. 数据应该来自正态分布的总体。

2. 等方差性：各组之间的方差应该是相等的。

3. 独立性：不同组之间的个体应该是相互独立的。

SPSS使用步骤以下是在SPSS中进行单因素方差分析的步骤。

步骤1：导入数据首先，打开SPSS软件并导入包含需要进行单因素方差分析的数据的文件。

选择“打开文件”选项，然后选择相应的数据文件。

步骤2：设置变量在SPSS中，我们需要将需要进行单因素方差分析的变量设置为“因子变量”（Factor Variable）。

选择“数据”菜单中的“变量视图”，然后选择需要进行单因素方差分析的变量，在“类型”一栏中选择“因子”。

步骤3：进行单因素方差分析选择“分析”菜单中的“比较手段”选项，然后选择“单因素方差”。

步骤4：指定变量在单因素方差分析对话框中，将需要进行分析的因子变量移动到“因子”框中。

步骤5：选项设置在单因素方差分析对话框中，可以设置一些可选参数，如：显示描述性统计信息、绘制盒须图等。

根据需要对这些选项进行设置。

步骤6：结果解读点击“确定”按钮后，SPSS将执行单因素方差分析并生成结果输出。

在输出窗口中，可以看到各组的均值、标准差和方差等统计指标。

同时，还会显示组间变异和组内变异的F统计量、p值和显著性水平。

结论单因素方差分析是一种用于比较多个组间均值差异的统计方法。

通过SPSS软件，我们可以轻松地进行单因素方差分析，并获取分析结果。

双因素方差
双因素方差分析,用于分析定类数据(2个)与定量数据之间的关系情况.例如研究人员性别,学历对于网购满意度的差异性;以及男性或者女性时,不同学历是否有着网购满意度差异性;或者同一学历时,不同性别是否有着网购满意度差异性.
双因素方差分析是相对于单因素方差分析而言;区别在于X(定类数据)的个数;如果仅为一个称为单因素方差;两个为双因素方差;单因素方差分析(即方差分析)的使用非常普遍;但双因素方差更多用于实验研究.
首先判断p值是否呈现出显著性,如果呈现出显著性,则说明X或者交互项对于Y有着差异(影响)关系.
分析结果表格示例如下(SPSSAU同时会生成拆线图):
备注：双因素方差分析基本上仅用于实验研究中，请谨慎使用。

SPSSAU操作截图如下：。

双因素方差分析spss实例双因素方差分析（ANOVA）是一种统计分析方法，它可以比较不同的组之间的投票者的结果，以确定两个或更多因素是否有显著的影响。

换句话说，它可以测量实验中的不同影响因素，以确定它们之间是否有显著的差异。

本文将介绍如何使用SPSS进行双因素方差分析，以确定两个因素之间是否有显著差异。

首先，需要准备你的数据，将其输入到SPSS程序中。

将你的数据文件保存为.csv格式，确保它的每列的标题是充分描述性的，并包括所有你所需要的因素。

一旦你的数据文件被保存到SPSS中，可以创建一个新的SPSS文件，然后将数据文件拖放到新的SPSS文件中即可。

接下来，在SPSS中，找到“统计”工具栏，点击进入“分析”选项卡。

找到“方差分析”，双击它，以进入“方差分析-双因素方差分析”窗口。

在“自变量”框中输入你要比较的两个因素，即你的实验的两个因素。

然后在“因子”菜单中选择“应变量的每个因子的水平”。

此时，SPSS将自动映射每个因素的水平，可以在“水平”窗口中查看。

现在，可以单击“方差分析”按钮，运行双因素方差分析。

SPSS 将给出结果表，该表显示在多个水平上，因素间是否存在显著差异。

在结果表中，F值说明了实验变量之间的差异。

当F值大于1时，实验变量存在显著差异，说明变量对结果有显著影响；反之，F值小于1时，实验变量没有显著差异，则表明变量对结果没有显著影响。

最后，你可以使用SPSS输出图表，根据结果表中的数据来分析两个因素之间的关系。

这也可以帮助你更好地理解实验结果，并更好地控制你的实验因素。

总之，SPSS双因素方差分析是一种很有用的统计工具，可以帮助研究者测量不同因素之间的关系，并确定它们之间是否存在显著差异。

上面介绍了如何使用SPSS进行双因素方差分析，并介绍了如何分析结果，希望对你有所帮助。

双因素方差分析spss双因素方差分析（Two-factor Analysis of Variance， ANOVA）是统计学中使用广泛的一种方法，它可以帮助我们测量并评估不同因素对试验结果的影响程度。

SPSS是一款统计数据处理软件，它也可以帮助我们进行双因素方差分析，即用于研究两个或多个因素的总体的差异以及它们之间的关系，而这个方法可以帮助我们更有效地弄清这两个因素之间的关系。

首先，我们需要准备好我们的数据，这样才能将它们可视化和分析。

建议使用Excel或者SPSS创建好表格，然后将数据导入表格中。

在导入数据之前，要确保将双因素分别设定为两个列，以便SPSS能够正确识别变量，此外还可以为每个变量指定不同的名称，以便在分析和结果展示时更容易理解。

接下来，在SPSS的Analysis菜单中，选择“General Linear Model”，然后选择“Univariate”，这样就可以开始分析了。

第一步就是在“Dependent Variable”部分，选择你想要分析的变量，然后点击“Options”，在“Means”选项中，可以看到因素的名称，选择它们，接着在“Post Hoc” 部分选择“Tukey”，然后点击“Continue”，完成设置。

随后，在“Output”界面中，点击“Save”，选择“Univariate”，勾选“Descriptive Statistics” 、“ANOVA” 和“Post Hoc Tests”，然后点击“OK”，SPSS 会生成一份包含描述性统计和分析结果的报告，我们可以根据报告内容进行进一步的分析和研究。

总之，使用 SPSS 进行双因素方差分析是一个简单易行、高效可靠的过程，可以帮助我们得出可靠的结论，以便做出合理的决策，并有助于识别实验变量之间的相关性和决定性。

SPSS分析：嵌套式两因素方差分析（单变量）1、数据输入格式⑴定义变量：国家品种最大光能转换效率注意：对圈红色的部分进行设定⑵输入数据：在Excel中编制下列格式数据，复制粘贴到SPSS中美国M56 0.842美国M56 0.829美国M56 0.83美国M56 0.834美国M49 0.849美国M49 0.844美国M49 0.851美国M49 0.839美国M5 0.822美国M5 0.82美国M5 0.822美国M5 0.817美国M34 0.849美国M34 0.852美国M34 0.853美国M34 0.844美国M64 0.865美国M64 0.855美国M64 0.862美国M64 0.852美国M73 0.853美国M73 0.856美国M73 0.851中国红运0.849中国红运0.849中国红运0.853中国香妃0.859中国香妃0.856中国香妃0.859中国香妃0.86中国新铁0.845中国新铁0.844中国新铁0.84中国新铁0.859中国新重瓣红0.837中国新重瓣红0.848中国新重瓣红0.854中国新重瓣红0.855中国新重瓣红0.856中国新重瓣红0.854中国交5 0.839 中国交5 0.834 中国交5 0.832 中国交5 0.834中国泽州1号0.845中国泽州1号0.832中国泽州1号0.835中国泽州1号0.8512、命令顺序：按下面图示选择后按“继续”键，进行其它设定选择继续后，按“确定”键即可弹出结果页面，导出为word文档即可。

UNIANOVA 最大光能转换效率 BY 国家品种 /METHOD=SSTYPE(1) /INTERCEPT=EXCLUDE /POSTHOC=国家品种(SNK DUNCAN LSD) /CRITERIA=ALPHA(0.05) /DESIGN=国家品种.。

双因素重复测量方差分析spss双因素重复测量方差分析(RM-ANOVA)是一种统计分析方法，可以用来检验两个或多个因素(变量)对实验结果的影响。

它可以让研究者预测实验中的一些不确定性，以便确定自变量和因变量之间的关系。

本文将介绍如何使用SPSS软件来进行双因素重复测量方差分析，并通过几个具体示例来帮助读者更好地理解。

首先，在SPSS中，双因素重复测量方差分析(RM-ANOVA)可以通过选择“分析”>“常规模型”>“双因素重复测量方差分析”来实现。

在设置参数之前，首先要选择变量名称，需要使用自变量（可以是多个），控制变量（可以是多个），和因变量（可以是多个）。

接下来要填写双因素重复测量方差分析的参数。

在此参数部分，研究者首先要在“因子A”输入框中输入自变量的数目，然后选择自变量的命令类型，有两种情况，一种是定性的和定量的，如果是定性的自变量，那么对单独的分类变量，就会自动编号，但是如果是定量的自变量，则需要用户输入取值范围。

之后，需要在“因子B”输入框中输入控制变量的数目，并选择控制变量的类型。

设置完参数之后，单击确定按钮。

SPSS将开始运行双因素重复测量方差分析，并将分析结果以报表的形式显示出来。

具体来说，可以看到实验组和控制组的统计摘要，并进行多项假设检验。

接下来，我们来看一个具体的例子，比如假设有一个实验，其中有两个自变量：视力（定量）和性别（定性），以及一个因变量：行为。

这样，在SPSS中，设置参数时，可以将“因子A”设置为定量自变量，取值范围是1-20，并将“因子B”设置为定性自变量，取值分为男性和女性两种。

完成双因素重复测量方差分析之后，SPSS将显示几项统计结果，如计算出的F值，以及相应的p值，以及来自实验组和控制组的具体数据。

如果F值大于1或p值小于0.05，则表明两个自变量对实验结果有显著影响，而控制组与实验组之间存在统计学显著性差异。

本文介绍了如何使用SPSS软件来进行双因素重复测量方差分析，主要介绍了双因素重复测量方差分析的设置参数，以及双因素重复测量方差分析的结果分析。