驻波

简述驻波的原理及应用驻波是指在空间中存在着振幅不变的波动形态。

驻波的形成原理是当一定频率的波在一条传播路径上来回传播时，由于波的传播速度和路径长度的关系，会导致传播的波和反射的波之间相互叠加，形成驻波。

驻波的形成需要满足两个条件：一是在传播路径的两端存在反射面；二是反射的波和传播的波之间具有相同的频率。

当满足这两个条件时，波在传播路径上来回传播，并且相互叠加形成稳定的波形。

驻波的形态与波长、路径长度以及传播速度等因素有关。

具体来说，如果传播路径长度为半个波长的整数倍，那么传播的波和反射的波在相遇时会互相叠加，形成干涉，波峰与波谷叠加，振幅增大，形成波形呈现出明显的节点和腹部。

这种现象称为驻波。

而当传播路径长度为波长的整数倍时，反射的波和传播的波处于相位同步，互相叠加形成稳定的波形。

驻波现象在物理学、电子学、声学等领域都有广泛的应用。

在物理学领域，驻波可以用于研究波动性质。

通过观察驻波的波形、节点和腹部的位置等特征，可以推断波的频率、波长和传播速度等参数。

此外，驻波还可以用于测量波速和频率。

例如，可以利用驻波现象来测量声波在空气中的传播速度。

在电子学领域，驻波可以用于研究电磁波的传播。

在传输线路或天线系统中，当传播的电磁波与反射的电磁波相遇时，会形成驻波。

通过观察驻波的波形，可以判断电磁波是否正常传输，以及传输线路是否匹配。

驻波比（VSWR）是衡量传输线路匹配程度的重要指标，通过测量驻波比可以评估传输线路的性能。

在声学领域，驻波可以用于控制声波的传播。

利用反射、折射和干涉等现象，可以设计出具有特定频率和波形的驻波系统。

这种系统被广泛应用于音乐演出、声学实验和工程设计等领域。

例如，乐器的共鸣腔体就是利用驻波原理来增强声音的产生和放大。

除了以上几个领域，驻波还在其他科学和工程领域有着重要的应用。

例如，在光学领域，驻波可以用于制造光纤和光波导器件，用于光通信和光器件的设计与制造；在微波领域，驻波可以用于微波谐振腔的设计与调谐，用于微波电路的设计与测试。

驻波知识点驻波是波动现象中的一个重要概念，广泛应用于电磁波、声波等领域。

了解驻波的基本概念和特性对于理解波动现象以及在实际应用中的运用具有重要意义。

本文将从基础概念、形成机制、特性以及实际应用等方面，分步骤地介绍驻波的知识点。

第一步：基础概念驻波是由两个相同频率、振幅相等但传播方向相反的波叠加而形成的一种特殊波动现象。

在驻波中，波动的节点（波幅为零）和波动的腹部（波幅最大）交替出现。

节点和腹部之间的距离被称为波长，而节点之间的距离则是半波长。

第二步：形成机制驻波的形成机制涉及波动的传播和干涉。

当两个波在同一介质中传播时，它们会相互干涉，形成驻波。

在这个过程中，来自两个方向的波经过反射、折射、散射等现象后，在特定位置上出现波动的叠加，形成了节点和腹部。

第三步：特性驻波具有一些独特的特性，其中最重要的特性是节点和腹部的分布。

节点是波动的位置，波幅为零。

相邻两个节点之间的距离是半波长。

相反，腹部是波动的位置，波幅达到最大。

腹部和节点之间的距离也是半波长。

此外，驻波还具有波动的稳定性和固定的频率。

第四步：实际应用驻波在实际应用中有广泛的用途。

其中一个重要应用是在电磁波领域中，如微波炉和天线。

微波炉利用驻波的节点和腹部形成热点，使食物迅速加热。

天线利用驻波的特性来增强信号的传输效果。

此外，在声学领域，如乐器制作和音响系统设计中，驻波也扮演着重要的角色。

总结驻波是一种特殊的波动现象，通过两个相同频率、振幅相等但传播方向相反的波叠加而形成。

了解驻波的基本概念、形成机制、特性以及实际应用对于理解波动现象和在实际应用中的运用具有重要意义。

驻波的知识点在电磁波、声波等领域中有广泛的应用，如微波炉和天线等。

通过深入学习和研究驻波，我们可以更好地理解波动现象，并在各个实际领域中应用这一知识点。

驻波的名词解释引言：在我们生活的世界中，科学与技术无处不在，而驻波作为一个重要的物理现象也深深影响着我们的生活。

本文将对驻波进行深入的解释与探讨，探寻其原理、应用以及对人类的重要意义。

一、驻波的基本概念驻波是指两个相同频率的波在空间中相互叠加形成的一种特殊的波动现象。

通常，驻波发生在有限空间内的传波系统中，是波的反射和干涉效应的结果。

由于波的叠加，形成了节点（波幅为零）和腹部（波幅为最大）等特点。

二、驻波的成因与原理驻波的成因可以通过波的叠加与干涉来进行理解。

当一条波沿一条导致终点反射回来的路径传播时，与被反射回来的波相遇，形成了驻波的节点（波幅为零）和腹部（波幅为最大）。

驻波的原理可以通过谐振来解释。

当波的传播速度和频率与传播介质的固有特性相匹配时，波在系统中的干涉会形成谐振。

这种谐振使得波的能量在系统内来回传播，并在节点和腹部间相互转换，最终形成驻波。

三、驻波的应用领域1. 音乐领域：驻波对于乐器的声音产生和音调调节起着至关重要的作用。

管乐器、弦乐器等都利用驻波来产生特定音调，并通过调节驻波节点位置来调整音高。

2. 无线通信：在无线通信领域，驻波可以用来进行天线调谐和匹配。

通过调整驻波节点的位置，可以提高天线和信号源之间的能量传输效率。

3. 光纤通信：驻波理论在光纤通信中也有广泛的应用。

通过合理设计光纤的直径和材料，可以实现光在光纤中的驻波传播，提高光纤通信的传输效率。

4. 药物研究与医学：在药物研究中，驻波可以用来研究分子间的相互作用和结构变化，加深我们对药物作用机制的理解。

在医学领域，驻波可以应用于体内成像技术，如超声波成像和磁共振成像，以便更准确地诊断和治疗疾病。

四、驻波的重要意义驻波作为一种波动现象，对于各个领域的科学研究和技术应用都具有重要意义。

它不仅有助于人们更好地理解波动现象和能量传播规律，还为科学家和工程师提供了一种可靠的方法来控制和利用波的特性。

在生活中，我们常常能观察到驻波现象。

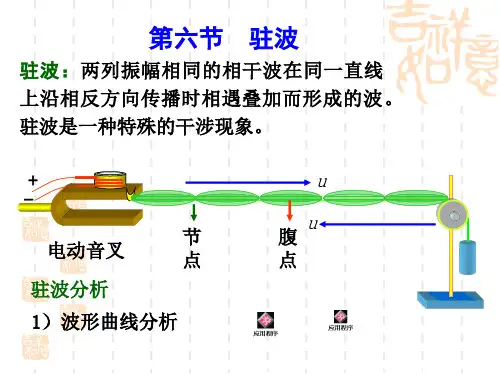
10.7 驻波教学目的1．知道驻波现象及什么是波节、波腹，驻波是一种特殊的干涉现象．2．理解驻波的形成过程，理解驻波与行波的区别，理解空气柱共鸣的条件．引入新课一列波在向前传播的途中遇到障碍物或者两种介质的分界面时，会发生反射，如果反射波和原来向前传播的波相互叠加，会发生什么现象呢？一、驻波1、驻波的演示:如课本图10－31所示，把弦线的一端A固定在电磁打点计时器的振针上，另一端跨过定滑轮拴一个砝码盘，盘上放砝码，将弦线拉平．在靠近定滑轮的B处，用一个尖劈把弦线支起来．接通电磁打点计时器的电源，振针振动时，有一列波向定滑轮的一侧传播，并在B处发生反射．改变尖劈的位置，来调节AB的长度，当尖劈调到某适当位置时，可以看到，弦线会分段振动起来．2、几个概念：①波节——弦线上有些点始终是静止不动的，这些点叫做波节．波腹——在波节和波节之间的那段弦线上，各质点以相同的频率、相同的步调振动，但振幅不同，振幅最大的那些点叫做波腹．在相邻的两段弦线上，质点的振动方向是相反的．相邻的两个波节(或波腹)之间的距离等于半个波长，即等于λ/2．②驻波——波形虽然随时间而改变，但是不向任何方向移动，这种现象叫做驻波．波形不传播，是媒质质元的一种集体振动形态。

"驻"字的第一层含义。

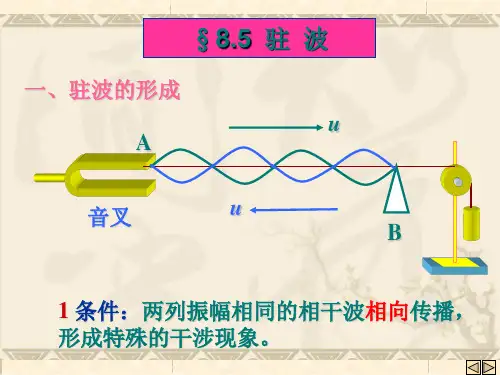
行波——驻波跟前面讲过的波形向前传播的那种波显然是不同的，相对于驻波来说波形向前传播的那种波叫行波．③驻波与行波的区别A物理意义不同：驻波是两列波的特殊干涉现象，行波是一列波在介质中的传播．B质点振动不同：相邻波节间质点运动方向一致．波节两侧质点振动方向总相反．C波形不同：波形向前传播的是行波，波形不向任何方向传播的是驻波．3、驻波的形成两列振幅相同的相干波在同一直线上沿相反方向传播时形成的叠加波。

①两列沿相反方向传播的振幅相同、频率相同的波叠加，形成驻波．②振幅相同、频率相同波的叠加．三、驻波的特点课本10－33中用虚线表示两列沿相反方向传播的振幅相同、频率相同波的叠加，用实线表示这两列波叠加后形成的合成波．图中画出了每隔T/8周期波形的变化情况．由图可以看出，合成波在波节的位置(图中的“·”表示)，位移始终为零．在两波节之间，各质点以相同的步调在振动，两波节之间的中点振幅最大，就是波腹(图中用“＋”表示)．驻波不是振动状态的传播，也没有能量的传播。

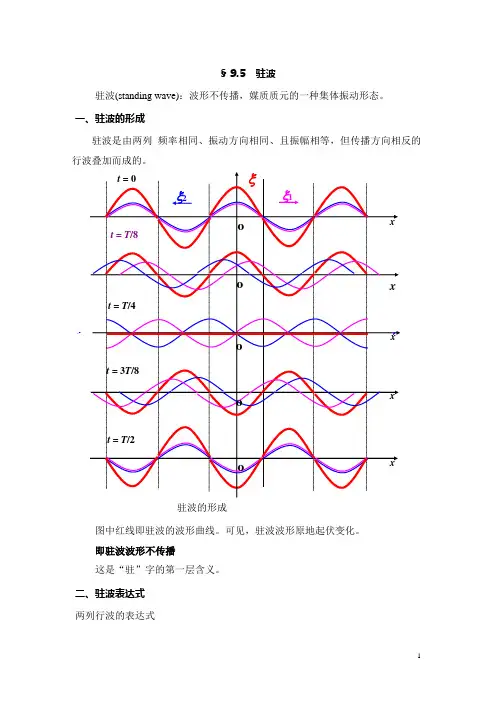
§ 9.5 驻波驻波(standing wave)：波形不传播，媒质质元的一种集体振动形态。

一、驻波的形成驻波是由两列 频率相同、振动方向相同、且振幅相等，但传播方向相反的行波叠加而成的。

图中红线即驻波的波形曲线。

可见，驻波波形原地起伏变化。

即驻波波形不传播这是“驻”字的第一层含义。

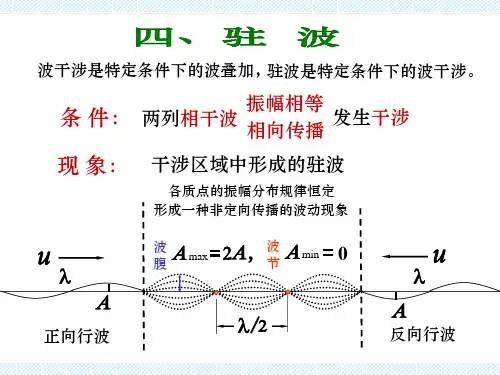
二、驻波表达式 两列行波的表达式 正向驻波的形成11cos 2π()x y A t νφλ=-+反向适当选择坐标原点和时间零点，使 ϕ1、ϕ2均等于零，则表达式变为 两行波叠加得驻波表达式：三、驻波的特点1 频率特点：由图及式知，各质元以同一频率作简谐振动。

2 振幅特点：(1)各点的振幅|2A cos kx |和位置x 有关，振幅在空间按余弦规律分布。

(2)波节：有些点始终静止，这些点称作波节(node)。

波节处，由两列波引起的两振动恰好反相，相互抵消，故波节处静止不动。

由cos 2π/x ＝0得波节位置，两相邻波节间的距离为 λ /2。

(3)波腹：有些点振幅最大，这些点称作波腹(antinode)。

波腹处，由两列波引起的两振动恰好同相，相互加强，故波腹处振幅最大。

由|cos kx |＝1得波腹位置，两相邻波腹间的距离亦为 λ /2。

3 相位特点驻波波形曲线分为很多“分段”(每段长λ/2)，同一分段中的各质元振动相位相同；相邻分段中的质元振动相位相反。

驻波相位不传播()m210,1,02im x k k A λ'=±+== 22cos 2π()xy A t νφλ=-+2cos 2π()xy A t νλ=+2cos 2πcos 2πxA tνλ=12y y y =+cos 2π()cos 2π()x xA t A t ννλλ=-++1cos 2π()xy A t νλ=+max0,1,22x kk A A λ'=±==这是“驻”字的第二层含义。

例： 为波节结论相邻波节间的各点同相 ,波节两边的各点振动反相 4 能量特点驻波的能量被“封闭”在相邻波节和波腹间 的λ/4的范围内，在此范围内有能量的反复 流动，但能量不能越过波腹和波节传播。

简述驻波的原理及应用一、驻波的原理驻波是指在一定空间范围内，由于波的反射和干涉造成的部分波的叠加而形成的一种特殊的波动现象。

驻波的形成需要满足波长、传播介质和边界条件等一系列条件。

驻波的原理可以通过以下几个关键概念来解释：1.反射：当波遇到边界时，如果边界是一个固定的位置或者形状不变的界面，波会被反射回去。

反射是驻波形成的基础。

2.干涉：当波遇到自己的反射波时，会产生干涉现象。

干涉可以使波的振幅增大或减小。

3.相位：波的相位是指波的起始位置和时间。

当波遇到反射波时，相位差会发生变化，从而影响波的叠加效果。

4.立体模式：波在空间中传播时，会形成一系列的立体模式，其中一些模式会在特定空间位置上形成驻波。

基于以上原理，我们可以得出驻波的特点：•驻波的振幅在某些位置上为零，这些位置被称为节点。

•驻波的振幅在某些位置上达到峰值，这些位置被称为腹部。

•驻波的节点和腹部交替出现。

二、驻波的应用驻波的原理在电磁波、声波等各个领域都有广泛的应用。

以下是几个常见的应用：1.音乐和声学：驻波可以在乐器的共鸣腔内产生，使乐器的声音更加丰满。

例如，管乐器中的空气柱会形成驻波，产生不同频率的音调。

2.照明：驻波在光学中的应用较少，但在光学波导中可以产生驻波，使传输效率更高。

3.无线通信：驻波在电磁波中的应用非常广泛。

例如，在传输线上产生驻波可以用于阻抗匹配，使信号能够更好地传输。

此外，驻波还可以用来检测和测量电缆中的故障。

4.医学成像：超声波成像中的驻波可以用于产生高分辨率的图像。

驻波可以改变回声信号的强度和频率，从而实现更详细的图像。

5.激光技术：激光中的驻波可以产生一系列的纵向模式。

这些模式可以选择性地放大，从而使激光更加稳定和一致。

综上所述，驻波作为一种特殊的波动现象，在不同的领域都有重要的应用价值。

通过理解驻波的原理，我们可以更好地应用它来解决实际问题。

驻波计算公式摘要：一、前言二、驻波概念介绍三、驻波计算公式1.驻波的产生原理2.驻波计算公式推导3.常见驻波计算公式类型四、驻波计算公式的应用1.无线通信系统中的应用2.声学系统中的应用3.地震学领域中的应用五、总结正文：【前言】驻波计算公式是物理学中的一个重要概念，涉及到声学、电磁学、地震学等多个领域。

本文将对驻波计算公式进行详细介绍，包括其产生原理、计算公式推导以及在不同领域的应用。

【驻波概念介绍】在了解驻波计算公式之前，我们需要先了解什么是驻波。

驻波，又称为静波或稳定波，是指在同一介质中，两个传播方向相反、振幅相同、频率相同的波相互叠加而形成的。

简单来说，驻波是一种特殊的波动现象，表现为波的振幅在某一范围内来回震荡。

【驻波计算公式】1.驻波的产生原理要理解驻波计算公式，我们首先要了解驻波是如何产生的。

假设有一列波沿着介质传播，当这列波遇到一个边界时，部分波将被反射回来。

如果反射波与入射波在同一介质中相遇，且二者具有相同的振幅和频率，那么它们就会相互叠加，形成驻波。

2.驻波计算公式推导驻波的计算公式涉及到波动方程，我们可以根据波动方程来推导驻波计算公式。

假设某一介质中的波速为v，波长为λ，则波动方程可以表示为：u/t = -ku/x其中，u表示波的振幅，t表示时间，x表示空间坐标，k = (2π/λ)v。

当波遇到边界并发生反射时，反射波的振幅与入射波的振幅之间的关系为：A_r = A_i * (1 - r)其中，A_i表示入射波的振幅，A_r表示反射波的振幅，r表示反射系数。

当反射波与入射波在同一介质中相遇时，它们会相互叠加，形成驻波。

设驻波的振幅为A_s，则有：A_s = A_i + A_r3.常见驻波计算公式类型在实际应用中，驻波计算公式有很多种，常见的有洛伦兹方程、尼克尔森方程等。

这些方程的具体形式可能因应用场景和问题的具体需求而有所不同，但它们的基本原理都是基于波动方程和反射系数来推导的。