下载文档原格式
................................--二二-―为理性思维和科学精神而教-评“利用单位圆的性质研究正弦函数、余弦函数的性质”课例计海荣，陈柏良（浙江省杭州市西湖高级中学）摘要：课例着眼于“素养导向”，通过“问题串”的设计，引导学生进行连续的思维活动，发展学生的数学核 心素养。
课例在问题优化、育人价值挖掘、“策略性知识”概括等方面可进行改进。
深刻领会本节教材的地 位、作用和教学价值，有利于合理把握数学核心素养培养的“切入点”和“着力点”。
关键词：理性思维；科学精神；教学设计文章编号：1002-2171 (2021)2-0024-03新课程实施以来，一线教师对“核心素养导向的 数学教学”进行了积极实践。
杭州学军中学第十四届 学术节以“核心素养导向的课堂转型”为主题，组织了 河北省衡水中学康红叶、浙江省杭州学军中学詹长刚、宁波市镇海中学王振全3位老师以人教A版 新教材《数学》(必修第一册）中的“利用单位圆的性质 研究正弦函数、余弦函数的性质”新授课内容为例进 行“同课异构”，给与会教师提供了 3节鲜活的课堂教 学案例。
本文以学军中学詹长刚老师的课堂实录为 例作一简评，同时谈谈笔者对本节课的数学理解和教 学设计中如何更好地发展学生数学核心素养的几点 拙见，与读者探讨。
1对本节课的简评1.1关注素养詹老师的教学设计，着眼于“素养导向”。
“问题 1”至“问题4”主要立足于“直观想象”核心素养的培养，后续利用单位圆对不等式“当〇<«<f时，则1< sin a+cos a<|”的证明，及“问题5”中对函数“/(a)=sin a+cos a”是否有最值的探究，培养学生的 逻辑推理核心素养，教学过程中比较重视提高学生的 观察和分析能力，体现了对数学运算核心素养的培养。
1.2问题驱动詹老师通过“问题串”的设计，促使学生实现对正 弦函数、余弦函数性质的自主发现。
www 2021年第2期中学数学教学参考（上旬）■0A课例:利用单彳圆的性质_研％正弦函数、余弦函数的性詹长刚（浙江省杭州学军中学）摘要：单位圆在三角函数中具有重要的意义，利用单位圆的性质来研究正弦函数、余弦函数的性质是定 义的深入理解，同时也能在研究的过程中提升学生的直观想象、数学抽象、逻辑推理、数学运算、数学建模 等核心素养。
关键词：单位圆；正弦函数；余弦函数；数学核心素养文章编号：1002-2171(2021)2-0019-052020年11月26日，在浙江省杭州学军中学第十 四届学术节暨第十二届校园文化节活动中，笔者同另 两位来自全国名校的教师进行了“利用单位圆的性质 研究正弦函数、余弦函数的性质”同课异构教学展不 活动，现将笔者的教学设计和课堂教学实录分享给大 家，敬请指正。
1内容和内容解析内容：利用单位圆研究正余弦函数的周期性、奇偶性、单调性、最值。
内容解析：前面已经学过三角函数的定义，并利 用定义得出了同角三角函数的基本关系和诱导公式，本节课主要利用单位圆的性质来分析探究，能够强化 数形结合思想，发现正弦函数、余弦函数的性质，同时求数列的前2»项和。
为偶数。
[〇n+\本题主要考査数列通项公式的求解、分组求和 法、指数型裂项求和、错位相减求和等，属于中等题。
高考以类比、拓展性知识为主线，设置能力型试题，实现数学的选拔功能。
这样的试题是第三轮复习中需 要重点关注的。
例7 (2020年高考数学上海卷第21题）有限数列{〇«}，若满足I—丨< 丨— “3I<…< U—a J是项数，则称满足性质/>。
(I )判断数列3,2,5，1和4,3,2,5，1是否具有 性质/>,请说明理由。
让学生体会数学知识的相互联系，激发学习兴趣。
2目标和目标解析目标：能够学会从单位圆的角度研究正弦函数、余弦函数的性质，体会数形结合思想的应用。
目标解析：达成目标的标志：一是能够准确地研究出正弦函 数、余弦函数的周期性、奇偶性、单调性、最值；二是能 够再发现正弦函数、余弦函数的其他性质；三是能够 类比研究出函数，如/(a)=sin a+cos a的单调性、最 值等。
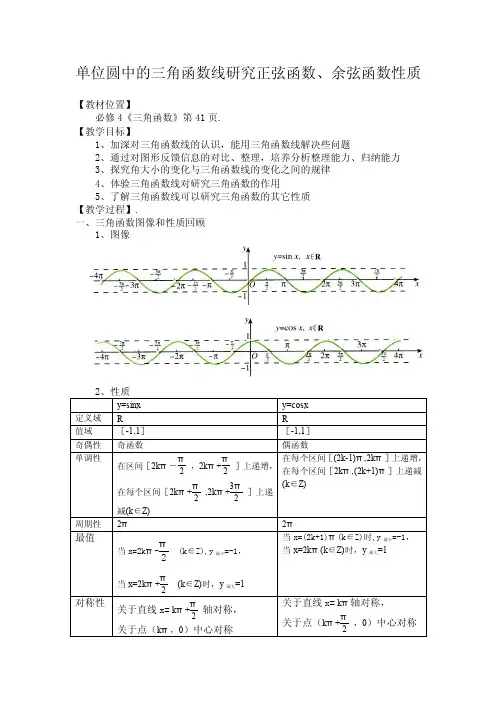
单位圆中的三角函数线研究正弦函数、余弦函数性质【教材位置】必修4《三角函数》第41页. 【教学目标】1、加深对三角函数线的认识，能用三角函数线解决些问题2、通过对图形反馈信息的对比、整理，培养分析整理能力、归纳能力3、探究角大小的变化与三角函数线的变化之间的规律4、体验三角函数线对研究三角函数的作用5、了解三角函数线可以研究三角函数的其它性质 【教学过程】.一、三角函数图像和性质回顾1、图像二、新授导入三角函数的性质可以观察图像得到.然而单位圆中的三角函数线能直观地表现了三角函数中的自变量与函数值之间的关系，因此三角函数线是研究三角函数性质的好工具.用三角函数线研究三角函数的性质体现了数形结合的思想方法，有利于我们从整体上把握有关性质.三、三角函数线设角α的终边与单位圆交与P点,与过点A(1,0)的单位圆切线交于T点(当终边与切线AT不相交时,取终边反向延长线与切线AT的交点),过P作PM垂直x轴于M,则有向线段MP,OM,AT,分别叫做角α的正弦线,余弦线,正切线.如图，正弦线为MP、余弦线为OM、正切线为AT.四、函数y=sinx、y=cosx的性质研究如图，在直角坐标系uOv中，角x的顶点与原点重合，始边与Ou轴重合，终边与单位圆交于点P（u，v）.过P作Ou轴的垂线，交Ou轴于M，得正弦线MP、余弦线OM.当角x的终边绕原点从Ou轴的正半轴开始，按照逆时针方向旋转时，正弦线MP按照0→1→0→－1→0→1…的规律周而复始地变化着.同时余弦线OM按照1→0→－1→0→1→0…的规律周而复始地变化着.由正弦线、余弦线的变化规律，得到：1、周期性自变量每增加π2（角x的终边旋转一周），正弦值（MP）、余弦值（OM）重复出现.2、奇偶性角x与角－x对应的正弦线关于Ou轴对称，余弦线重合.五、讨论诱导公式六、利用三角函数线解题1、比较sin400与sin1350大小. 解：sin1350= sin450如图：450角的正弦线大于400角的正弦线， 故sin400<sin13502、已知sin α21≥，求角α的集合.解：在单位圆中，角π6和5π6的正弦线长度为21，因为sin α21≥，即角α正弦线长度大于21，所以角α在π6 和5π6之间， 故角α的集合为⎭⎬⎫⎩⎨⎧∈+<<+Z k k k ,26526ππαππα.。
