图与网络模型实验
- 格式:pptx
- 大小:3.03 MB
- 文档页数:25

图与网络的运筹学实验报告图与网络的运筹学实验报告引言:图与网络是运筹学中的重要概念,它们在各个领域中都有广泛的应用。
本实验旨在通过实际案例,探讨图与网络在运筹学中的应用,并通过运筹学方法对问题进行求解和优化。
一、图与网络的基本概念1.1 图的定义与表示图是由节点和边组成的数学模型,它可以用来描述各种实际问题。
图可以用邻接矩阵或邻接表等方式进行表示。
1.2 网络的定义与分类网络是图的一种特殊形式,它的边具有权重或容量等属性。
根据边的属性不同,网络可以分为最短路径网络、最小生成树网络、最大流网络等。
二、图与网络在运筹学中的应用2.1 最短路径问题最短路径问题是图与网络中的经典问题之一。
通过运筹学方法,可以求解两点之间的最短路径,并找到最优解。
2.2 最小生成树问题最小生成树问题是在图中找到一棵包含所有节点的树,并使得树的边权重之和最小。
通过运筹学方法,可以有效地解决最小生成树问题。
2.3 最大流问题最大流问题是在网络中找到从源节点到汇节点的最大流量。
通过运筹学方法,可以确定网络中的最大流,并进行优化。
三、实际案例分析3.1 交通网络优化以城市交通网络为例,通过建立图模型,可以对交通流量进行优化调度,减少交通拥堵和能源消耗。
3.2 物流配送优化以物流配送为例,通过建立网络模型,可以优化货物运输路径,减少运输成本和时间。
3.3 电力网络优化以电力网络为例,通过建立图模型,可以优化电力输送路径,提高电网的稳定性和可靠性。
四、运筹学方法的求解4.1 最短路径求解算法常用的最短路径算法有Dijkstra算法和Floyd-Warshall算法,它们可以高效地求解最短路径问题。
4.2 最小生成树求解算法常用的最小生成树算法有Prim算法和Kruskal算法,它们可以高效地求解最小生成树问题。
4.3 最大流求解算法常用的最大流算法有Ford-Fulkerson算法和Edmonds-Karp算法,它们可以高效地求解最大流问题。


第1篇一、实验背景随着信息技术的飞速发展,模型网络算法在各个领域都得到了广泛应用。
为了深入了解模型网络算法的原理和应用,我们设计并完成了一次模型网络算法实验。
本次实验旨在通过构建一个简单的模型网络,学习并验证模型网络算法在数据处理和模式识别等方面的性能。
二、实验目的1. 理解模型网络算法的基本原理;2. 掌握模型网络算法的实现方法;3. 评估模型网络算法在不同数据集上的性能;4. 分析模型网络算法的优缺点。
三、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 库:NumPy、Scikit-learn、Matplotlib4. 数据集:Iris数据集、MNIST数据集四、实验内容1. 模型网络算法概述模型网络算法是一种基于图论的算法,通过构建模型网络来模拟真实世界中的复杂关系。
模型网络由节点和边组成,节点代表实体,边代表实体之间的关系。
模型网络算法可以用于数据分析、模式识别、知识图谱构建等领域。
2. 模型网络算法实现本次实验采用Python编程语言实现模型网络算法。
具体步骤如下:(1)加载数据集:从Iris数据集和MNIST数据集中获取数据。
(2)构建模型网络:根据数据集的特征,构建模型网络。
例如,在Iris数据集中,可以按照花种类型构建节点,按照特征值构建边。
(3)模型网络算法:使用模型网络算法对数据进行处理。
例如,使用PageRank算法计算节点的权重,使用链接预测算法预测节点之间的关系。
(4)性能评估:使用准确率、召回率、F1值等指标评估模型网络算法在不同数据集上的性能。
3. 实验结果与分析(1)Iris数据集在Iris数据集上,我们使用PageRank算法计算节点的权重,并使用链接预测算法预测节点之间的关系。
实验结果显示,模型网络算法在Iris数据集上的准确率达到80%以上。
(2)MNIST数据集在MNIST数据集上,我们使用模型网络算法对图像进行分类。
实验结果显示,模型网络算法在MNIST数据集上的准确率达到90%以上。

18
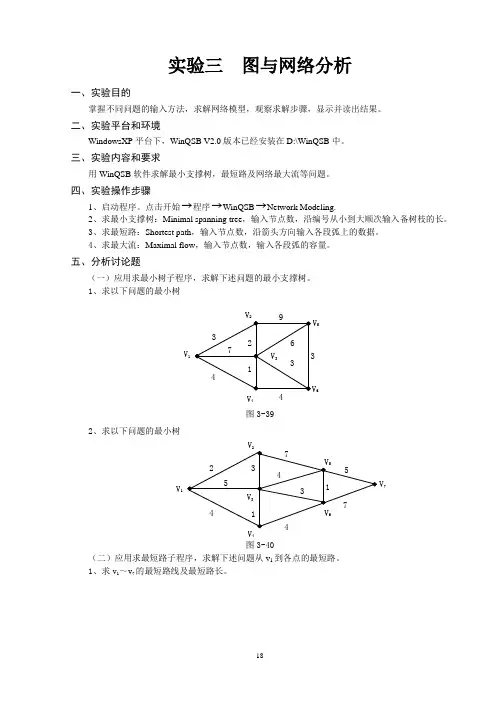
实验三 图与网络分析
一、实验目的
掌握不同问题的输入方法,求解网络模型,观察求解步骤,显示并读出结果。
二、实验平台和环境
WindowsXP 平台下,WinQSB V2.0版本已经安装在D:\WinQSB 中。
三、实验内容和要求
用WinQSB 软件求解最小支撑树,最短路及网络最大流等问题。
四、实验操作步骤
1、启动程序。
点击开始→程序→WinQSB →Network Modeling.
2、求最小支撑树:Minimal spanning tree ,输入节点数,沿编号从小到大顺次输入备树枝的长。
3、求最短路:Shortest path ,输入节点数,沿箭头方向输入各段弧上的数据。
4、求最大流:Maximal flow ,输入节点数,输入各段弧的容量。
五、分析讨论题
(一)应用求最小树子程序,求解下述问题的最小支撑树。
1、求以下问题的最小树
图3-39
2、求以下问题的最小树
图3-40
(二)应用求最短路子程序,求解下述问题从v 1到各点的最短路。
1、求v 1~v 7的最短路线及最短路长。
19
图3-41
2、求v 1~v 12的最短路线及最短路长。
图3-42
(三)应用求最大流的子程序,求解下述问题从v s 到v t 的网络最大流,图中弧旁数字为容量c ij 。
1、求以下网络的最大流
图3-43
2、求以下网络的最大流
图3-44
六、图论模型常用术语词汇及其含义
20。


图的应用及建立实验心得图是离散数学中的一种数学模型,在现实生活中有着广泛的应用。
图的应用包括社交网络分析、物流规划、路径优化、电路设计等等。
在进行图的应用研究时,我参与了一个实验项目,通过构建虚拟社交网络的图模型,来分析社交网络的特征以及推荐算法的效果。
在这个实验中,我积累了一些宝贵的心得体会。
首先,建立图模型需要明确目标和需求。
在实验之前,我们需要明确研究的问题和目标,并针对性地选择图的类型和构建方法。
比如,在社交网络分析中,我们可以选择无向图来表示社交关系,也可以选择有向图来表示信息传播。
根据实验的目标,我们可以选择使用邻接矩阵或邻接表来表示图的结构。
一个清晰的目标能够帮助我们更好地选择合适的图模型和算法。
其次,进行实验前,需要收集和处理数据。
在我们的实验中,我们使用了虚拟数据来构建社交网络图。
数据的质量和准确性对于实验结果的可靠性至关重要。
在收集数据时,我们要注意保护用户的隐私,确保数据的合法性。
在处理数据时,我们要进行必要的清洗和预处理,以保证数据的完整性和准确性。
这样才能够获得可靠的实验结果。
然后,需要选择合适的图算法来分析和处理图数据。
在我们的实验中,我们需要通过社交网络图来评估不同的推荐算法的效果。
因此,我们选择了一些经典的图算法,如最短路径算法和最小生成树算法。
这些算法能够帮助我们提取和分析图数据的特征。
在选择算法时,我们要充分考虑实验的目标和数据的特点,选择合适的算法来解决问题。
最后,需要对实验结果进行评估和反思。
在我们的实验中,我们通过比较不同推荐算法的效果,来评估它们的性能和可靠性。
并通过对实验结果的分析,我们可以对算法和模型的优化提出一些改进方案。
在反思过程中,我们还可以总结出一些经验和教训,以便今后的实验工作。
通过参与这个实验项目,我对图的应用有了更深入的理解,并积累了一些实践经验。
我认识到,在图的应用中,选择合适的图模型和算法非常重要,只有清晰地确定问题和目标,并选择合适的方法,才能取得良好的实验效果。

实验七图论模型一、实验目的掌握不同问题的输入方法,求解网络模型,观察求解步骤,显示并读出结果。
二、实验平台和环境Windows9X/ME/NT/2000/XP平台下,WinQSB V1.0版本已经安装在D:\WinQSB中。
三、实验内容和要求用WinQSB软件求解最小支撑树,最短路及网络最大流等问题。
四、实验操作步骤6.4.1启动程序。
点击开始→程序→WinQSB→Network Modeling.6.4.2求最小支撑树。
6.4.2.1分析例题。
点击File→Load Problem,打开文件,系统显示如图7-1所示的界面。
点击菜单栏Solve and Analyze或点击工具栏中的图标,观赏一下软件求解的过程。
图7-16.4.2.2实例操作。
例6.1某工厂内联结六个车间的道路网如图7-2所示。
已知每条道路的长,要求沿道路架设联结六个车间的电话线网,使电话线的总长最小。
1、启动程序。
点击开始→程序→WinQSB→Network Modeling,系统显示如图7-3所示的界面。
图7-32、建立新问题(点击File→New Problem),显示如图7-4所示的界面。
图7-4选择Minimal Spanning Tree,输入标题名、网络节点数,选择表格输入形式(spreadsheet matrix form),边弧权数转换(symmetric arc coefficients)可选可不选,如图7-5所示界面。
图7-53、输入数据。
在图7-5中输入各节点之间的权数,一般按照从小下标节点到大下标节点的原则输入权数,并且在输入过程中按Tab键或方向键即可输入下一个单元格。
如图7-6所示。
图7-64、修改参数。
1)修改标题名和节点名。
系统默认节点名称为node1,node2,……,noden。
如果对默认名不满意可以进行修改,点击菜单栏Edit,下拉菜单有两个修改选项:修改标题名(Problem Name)和节点名(Node Name)。

第五章 图与网络模型及方法§1 概论图论起源于18世纪。
第一篇图论论文是瑞士数学家欧拉于1736 年发表的“哥尼斯堡的七座桥”。
1847年,克希霍夫为了给出电网络方程而引进了“树”的概念。
1857年,凯莱在计数烷22 n n H C 的同分异构物时,也发现了“树”。
哈密尔顿于1859年提出“周游世界”游戏,用图论的术语,就是如何找出一个连通图中的生成圈,近几十年来,由于计算机技术和科学的飞速发展,大大地促进了图论研究和应用,图论的理论和方法已经渗透到物理、化学、通讯科学、建筑学、生物遗传学、心理学、经济学、社会学等学科中。
图论中所谓的“图”是指某类具体事物和这些事物之间的联系。
如果我们用点表示这些具体事物,用连接两点的线段(直的或曲的)表示两个事物的特定的联系,就得到了描述这个“图”的几何形象。
图论为任何一个包含了一种二元关系的离散系统提供了一个数学模型,借助于图论的概念、理论和方法,可以对该模型求解。
哥尼斯堡七桥问题就是一个典型的例子。
在哥尼斯堡有七座桥将普莱格尔河中的两个岛及岛与河岸联结起来问题是要从这四块陆地中的任何一块开始通过每一座桥正好一次,再回到起点。
当然可以通过试验去尝试解决这个问题,但该城居民的任何尝试均未成功。
欧拉为了解决这个问题,采用了建立数学模型的方法。
他将每一块陆地用一个点来代替,将每一座桥用连接相应两点的一条线来代替,从而得到一个有四个“点”,七条“线”的“图”。
问题成为从任一点出发一笔画出七条线再回到起点。
欧拉考察了一般一笔画的结构特点,给出了一笔画的一个判定法则:这个图是连通的,且每个点都与偶数线相关联,将这个判定法则应用于七桥问题,得到了“不可能走通”的结果,不但彻底解决了这个问题,而且开创了图论研究的先河。
图与网络是运筹学(Operations Research )中的一个经典和重要的分支,所研究的问题涉及经济管理、工业工程、交通运输、计算机科学与信息技术、通讯与网络技术等诸多领域。
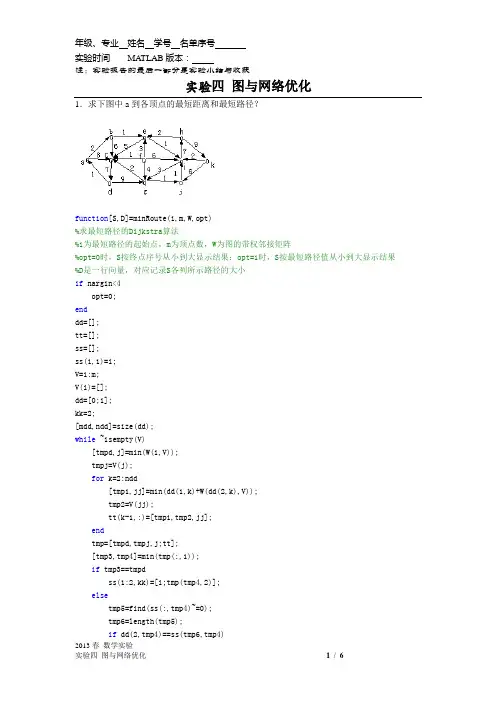
实验四图与网络优化1.求下图中a到各顶点的最短距离和最短路径?function[S,D]=minRoute(i,m,W,opt)%求最短路径的Dijkstra算法%i为最短路径的起始点,m为顶点数,W为图的带权邻接矩阵%opt=0时,S按终点序号从小到大显示结果;opt=1时,S按最短路径值从小到大显示结果%D是一行向量,对应记录S各列所示路径的大小if nargin<4opt=0;enddd=[];tt=[];ss=[];ss(1,1)=i;V=1:m;V(i)=[];dd=[0;i];kk=2;[mdd,ndd]=size(dd);while ~isempty(V)[tmpd,j]=min(W(i,V));tmpj=V(j);for k=2:ndd[tmp1,jj]=min(dd(1,k)+W(dd(2,k),V));tmp2=V(jj);tt(k-1,:)=[tmp1,tmp2,jj];endtmp=[tmpd,tmpj,j;tt];[tmp3,tmp4]=min(tmp(:,1));if tmp3==tmpdss(1:2,kk)=[i;tmp(tmp4,2)];elsetmp5=find(ss(:,tmp4)~=0);tmp6=length(tmp5);if dd(2,tmp4)==ss(tmp6,tmp4)实验四图与网络优化 ss(1:tmp6+1,kk)=[ss(tmp5,tmp4);tmp(tmp4,2)];elsess(1:3,kk)=[i;dd(2,tmp4);tmp(tmp4,2)];endenddd=[dd,[tmp3;tmp(tmp4,2)]];V(tmp(tmp4,3))=[];[mdd,ndd]=size(dd);kk=kk+1;endif opt==1[tmp,t]=sort(dd(2,:));S=ss(:,t);D=dd(1,t);elseS=ss;D=dd(1,:);end>> clear all>> w=inf*ones(11);>> w(1,[2,3])=[2,8];>> w(2,[3,5])=[6,1];>> w(3,[4])=[7];>> w(4,[1,7])=[1,9];>> w(5,[3,9])=[5,1];>> w(6,[3,5,7,9])=[1,3,4,6];>> w(7,[3,10])=[2,1];>> w(8,[5,11])=[2,9];>> w(9,[7,8])=[3,7];>> w(10,[9])=[1];实验四图与网络优化>> w(11,[9,10])=[2,6];>> [s,d]=minRoute(1,11,w)s =1 1 1 1 1 1 1 1 1 1 10 2 2 2 2 3 2 2 3 2 60 0 5 5 5 0 5 5 4 5 00 0 0 9 9 0 9 9 0 9 00 0 0 0 7 0 7 8 0 8 00 0 0 0 0 0 10 0 0 11 0d =0 2 3 4 7 8 8 11 15 20 Inf因此,按顶点序号a-b; a-b-e; a-b-e-i; a-b-e-i-g; a-c; a-b-e-i-g-j; a-b-e-i-h; a-c-d; a-b-e-i-h-k; a-f; 按上面次序最短距离分别是0 2 3 4 7 8 8 11 15 20 Inf2.一辆货车从水泥厂运水泥至某建筑工地。
课内实验报告课程名:运筹学任课教师:邢光军专业:学号:姓名:/ 学年第学期南京邮电大学管理学院实验背景:求下图中v 1到v 6的最短路。
实验结果:一:问题分析和建立模型:用EXCEL 求解最短路的原理是:令最短路径变量为0或1.即如果最短路通过某弧,则该变量为1,否则为0,如最短路径为v1v2->v3v4->v4v6,那么最短路径变量v1v3=1,v3v4=1,v4v6=1,其余的为0.约束条件为起点的进出权数和为1,终点是-1。
除了起点和终点,其余每个中间节点的进出权数之和为0。
目标函数则为各弧的权数与对应的最短路径变量乘积之和。
于是可以转化规划求解最短路径。
二:计算过程:下面利用Spreadsheet 来求解该问题:在Excel2003版本中,单击“工具”栏中“加载宏”命令,在弹出的的“加载宏”对话框选择“规划求解”,在“工具”下拉菜单中会增加“规划求解”命令,这样就可以使用了。
利用EXCEL 求解题中v1到v6的最短路。
第一步,在Excel 上建立最短路模型,将所有的弧列出来,如图①中的A 和B 两列,所有弧的权数如C 列所示,并令最短路径变量的初始值为0,如D 列所示。
节点v1到v6的进出和如G 列所示。
(G2=D2+D3+D4.G3=D5-D2-D7,G4=D6-D3-D9,G5=D7+D8-D4-D6-D10,G6=D9+D10+D11,G7=-D5-D8-D11)。
目标函数为SUMPRODUCT (C2:C11,D2:D11)。
v 235 2 7 5 3 1 5 1 2v 1v 6v 5 v 3 v 4图①第二步,单击“规划求解”按钮,设置目标单元格为最小值,设置可变单元格为最短路径变量单元格,添加约束条件,如图②所示。
图②第三步,单击“求解”按钮,选择“保存规划求解结果”。
如图③。
图③三:结果分析:图③中D列为1的变量表示最短路径经过的弧,得到最短的路径为v1->v3->v4->v6,最短路长为8。
实验六:图与网络分析-最短路问题
一、实验目的:掌握不同问题的输入方法,求解网络模型,观察求解步骤,显示并读出结果。
二、内容和要求:用WinQSB软件求解最短路问题,并对结果进行简单分析。
例:求下图的最短路。
三、操作步骤:
1.“开始”菜单→“winQSB”→“Network Modeling”(网络模型)。
2.建立新问题:File→New Problem,出现下面界面。
选择Shortest Path Problem、Minimization、输入问题标题、节点的个数,然后单击“OK”。
3.修改节点名称:菜单“Edit”→“Node Names”,编辑完点“OK”,如下图。
4.按下图输入图的权矩阵,本例是无向图,每一条边必须输入两次。
5.菜单“Solve and Analyze”→“Solve the Problem”,出现以下对话框,
6.然后选择起点v1和终点v10,点“Solve”按键,出现下图:
从图中可以看到v1到v10的最短路径为v1→v3→v7→v10,总长为6,另外从v1到其他各点的最短距离也都计算了出来。
7.实例求解:有九个城市v1,v2…,v9,其公路网如下图,弧旁数字是该段公路的长度,有一批货物从v1运到v9,试用Dijkstra方法求出走哪条路最短?
自己先用标号法求出最短路,然后用winWSB软件进行验证。
8.思考题:教育部门打算在某新建城区建一所学校,让附近七个居民区的学生就近入学。
七个居民区之间的道路如下图所示,学校应建在哪个居民区,才能使大学都方便?(图中距离单位:百米)。