CRC校验算法-程序例子
- 格式:docx
- 大小:14.01 KB
- 文档页数:2

CRC校验算法及C#程序实现CRC校验可以运用于传输数据过程中的验证,发送端发送有效数据时,先根据有效数据和生成多项式(比如CCITT标准的多项式是X16+X12+X5+1)计算出CRC校验码,把CRC校验码加到有效数据后面一起发送;当接收数据时,取出前面有效数据部分,用同样生成多项式计算出CRC校验码,然后取出接收数据后面CRC校验码部分,对比两个校验码是否相同。
如果相同,认为接收到的数据与发送的数据是一致的,传输正确;如果不同,认为传输数据出错。
CRC(循环冗余校验)算法主要是一个计算除法的过程。
算法有两个输入值,第一个是输入的信号,这通常是一个很长的数据,作为被除数。
第二个是一个与具体的CRC算法相关的多项式,称为生成多项式,用作除数。
基本的计算过程是,两者作模2除法(本质上是对应位做异或运算),余数就是CRC校验码的结果。
I、基本算法(人工笔算):以CRC16-CCITT为例进行说明,它的生成多项式是X16+X12+X5+1,CRC校验码为16位,生成多项式17位。
假如数据流为4字节:BYTE[3]、BYTE[2]、BYTE[1]、BYTE[0];数据流左移16位,相当于扩大256×256倍,再除以生成多项式0x11021,做不借位的除法运算(相当于按位异或),所得的余数就是CRC校验码。
发送时的数据流为6字节:BYTE[3]、BYTE[2]、BYTE[1]、BYTE[0]、CRC[1]、CRC[0];II、计算机算法1(比特型算法):1)将扩大后的数据流(6字节)高16位(BYTE[3]、BYTE[2])放入一个长度为16的寄存器;2)如果寄存器的首位为1,将寄存器左移1位(寄存器的最低位从下一个字节获得),再与生成多项式的简记式异或;否则仅将寄存器左移1位(寄存器的最低位从下一个字节获得);3)重复第2步,直到数据流(6字节)全部移入寄存器;4)寄存器中的值则为CRC校验码CRC[1]、CRC[0]。


CRC校验计算方法1、循环校验码(CRC码):是数据通信领域中最常用的一种差错校验码,其特征是信息字段和校验字段的长度可以任意选定。
2、生成CRC码的基本原理:任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’和‘1’取值的多项式一一对应。
例如:代码1010111对应的多项式为x6+x4+x2+x+1,而多项式为x5+x3+x2+x+1对应的代码101111。
3、CRC码集选择的原则:若设码字长度为N,信息字段为K位,校验字段为R位(N=K+R),则对于CRC码集中的任一码字,存在且仅存在一个R次多项式g(x),使得V(x)=A(x)g(x)=x R m(x)+r(x);其中: m(x)为K次信息多项式, r(x)为R-1次校验多项式,g(x)称为生成多项式:g(x)=g0+g1x+g2x2+...+g(R-1)x(R-1)+g R x R发送方通过指定的g(x)产生CRC码字,接收方则通过该g(x)来验证收到的CRC码字。
标准CRC生成多项式如下表:名称生成多项式简记式* 标准引用CRC-4 x4+x+1 3 ITU G.704CRC-8 x8+x5+x4+1 0x31CRC-8 x8+x2+x1+1 0x07CRC-8 x8+x6+x4+x3+x2+x1 0x5ECRC-12 x12+x11+x3+x+1 80FCRC-16 x16+x15+x2+1 8005 IBM SDLCCRC16-CCITT x16+x12+x5+1 1021 ISO HDLC, ITU X.25, V.34/V.41/V.42, PPP-FCSCRC-32 x32+x26+x23+...+x2+x+1 04C11DB7 ZIP, RAR, IEEE 802 LAN/FDDI, IEEE 1394, PPP-FCSCRC-32c x32+x28+x27+...+x8+x6+1 1EDC6F41 SCTP基本算法(人工笔算):以CRC16-CCITT为例进行说明,CRC校验码为16位,生成多项式17位。

CRC循环冗余校验是一种用于检测数据传输过程中可能出现的错误的方法。
以下是一个简单的CRC循环冗余校验的例子:
假设我们有一个8位的数据块,其内容为01010101。
1.首先,我们选择一个生成多项式,例如CRC-8的生成多项式为X^8 + X^2 + X^1 + X^0。
2.将数据块左移8位,得到101010100。
3.对数据块进行模2除法,用生成多项式去除数据块。
在这个例子中,101010100除以X^8 + X^2 + X^1 + X^0得到余数0001。
4.将余数添加到数据块的末尾,得到新的数据块101010100001。
5.将新的数据块发送给接收方。
接收方收到数据块后,重复上述步骤:
1.对接收到的数据块进行模2除法,用生成多项式去除数据块。
2.如果余数为0,则说明数据块在传输过程中没有出现错误;如果余数不为0,则说明数据块在传输过程中出现了错误。
这个例子展示了CRC循环冗余校验的基本原理。
在实际应用中,CRC算法会更加复杂,但基本原理是相同的。
python实现CRC(循环冗余)校验循环冗余校验码(CRC),简称循环码,是⼀种常⽤的、具有检错、纠错能⼒的校验码,在早期的通信中运⽤⼴泛。
循环冗余校验码常⽤于外存储器和计算机同步通信的数据校验。
奇偶校验码和海明校验码都是采⽤奇偶检测为⼿段检错和纠错的(奇偶校验码不具有纠错能⼒),⽽循环冗余校验则是通过某种数学运算来建⽴数据位和校验位的约定关系的。
这⾥我⽤CRC-16/MODBUS作为例⼦,多项式 POLY(Hex):8005,初始值INIT(Hex):FFFF,结果异或值XOROUT(Hex):0000,具体代码如下:#多项式 POLY(Hex):8005,初始值 INIT(Hex):FFFF,结果异或值 XOROUT(Hex):0000def crc16Add(read):crc16 = crcmod.mkCrcFun(0x18005, rev=True, initCrc=0xFFFF, xorOut=0x0000)data = read.replace(" ","")readcrcout =hex(crc16(unhexlify(data))).upper()str_list =list(readcrcout)if len(str_list)==5:str_list.insert(2,'0')# 位数不⾜补0crc_data ="".join(str_list)crc_data =int(crc_data[2:],16)crc_data ="%04x"% crc_dataread = read.strip()+ crc_dataprint('增加Modbus_CRC16校验:>>>', read)return read。

CRC校验算法的实例解析概念 CRC校验算法,说⽩了,就是把需要校验的数据与多项式进⾏循环异或(XOR),进⾏XOR的⽅式与实际中数据传输时,是⾼位先传、还是低位先传有关。
对于数据⾼位先传的⽅式,XOR从数据的⾼位开始,我们就叫它顺序异或吧;对于数据低位先传的⽅式,XOR从数据的低位开始,我们就叫它反序异或吧。
两种不同的异或⽅式,即使对应相同的多项式,计算出来的结果也是不⼀样的。
实例解析 两种不同类型的写法:#include <stdio.h>typedef unsigned char uint8_t;uint8_t gencrc(uint8_t *data, size_t len){uint8_t crc = 0xff;size_t i, j;for (i = 0; i < len; i++) {crc ^= data[i];for (j = 0; j < 8; j++) {if ((crc & 0x80) != 0)crc = (uint8_t)((crc << 1) ^ 0x31);elsecrc <<= 1;}}return crc;}/*crc8 poly = 0x107 (x8+x2+x1+1)*/uint8_t crc8(uint8_t *data, int size){uint8_t crc = 0x00;uint8_t poly = 0x07;int bit;while (size--){crc ^= *data++;for (bit = 0; bit < 8; bit++){if (crc & 0x80){crc = (crc << 1) ^ poly;}else{crc <<= 1;}}}return crc;}int main(){uint8_t data[8] = {0xBE,0xEF,0,0,0,0,0,0};uint8_t datab[8] = {0xBE,0xEF,2,0,0,0,0,0};uint8_t crc,crcb;crc = gencrc(data, 8);crcb = gencrc(datab, 8);printf("first crc:\n");printf("crc:0x%1x crcb:0x%x \n", crc,crcb);crc = crc8(data, 8);crcb = crc8(datab, 8);printf("second crc:\n");printf("crc:0x%1x crcb:0x%x \n", crc,crcb);crc = gencrc(data+2, 1); /* returns 0xac */printf("%1x\n", crc);return 0;} 参数不同结果:first crc:crc:0xc7 crcb:0x69 second crc:crc:0x83 crcb:0xd1 ac。

CRC常见算法的C语言实现CRC(Cyclic Redundancy Check)是一种常见的数据校验算法,用于检测或校正以循环方式传输的数据中的错误。
CRC算法在通信、存储、校验等领域得到广泛应用。
以下是CRC常见算法的C语言实现示例。
1.CRC-8校验算法:```// CRC-8 polynomial: x^8+x^2+x+1 (0x07)unsigned char crc8(const unsigned char *data, unsigned int length)unsigned char crc = 0;for (unsigned int i = 0; i < length; i++)crc ^= data[i];for (unsigned int j = 0; j < 8; j++)if (crc & 0x80)crc = (crc << 1) ^ 0x07;elsecrc <<= 1;}}return crc;```2.CRC-16校验算法:```// CRC-16 polynomial: x^16+x^15+x^2+1 (0x8005)unsigned short crc16(const unsigned char *data, unsigned int length)unsigned short crc = 0;for (unsigned int i = 0; i < length; i++)crc ^= (unsigned short)data[i] << 8;for (unsigned int j = 0; j < 8; j++)if (crc & 0x8000)crc = (crc << 1) ^ 0x8005;elsecrc <<= 1;}}return crc;```3.CRC-32校验算法:```// CRC-32 polynomial: 0x04c11db7unsigned int crc32(const unsigned char *data, unsigned int length)unsigned int crc = 0xFFFFFFFF;for (unsigned int i = 0; i < length; i++)crc ^= data[i];for (unsigned int j = 0; j < 8; j++)if (crc & 1)elsecrc >>= 1;}}return ~crc;```以上是常见的CRC校验算法的C语言实现示例。

crc校验码计算例题
奇偶校验
这个校验主要的应用场景是ASCII码的校验,因为ASCII一共有128个,所以只需要7位足够了,但是计算机基本按照字节存储,所以自然而然多出来一位,也就是8位。
那么左边的那个bit位就可以用来做奇偶校验位置了。
核心思想:对信息位中的1进行异或运算,然后根据这个异或结果和奇偶校验的方法决定校验位的值。
汉明码
分组形成校验关系
校验位取值并计算最后的结果
所有计算机组成的书上这个计算过程根本就写不明白,这里我推荐利用表格计算,以1010为例:
利用公式计算位数[公式] 解得k为3
计算分布([公式] )
分组形成校验关系
这里直接用表格计算就行了
关于校验
校验计算完成以后根据[公式] 的值检查是否有问题,如果全为0则没有问题,如果不为0,则转换为10进制,所代表的就是这个十进
制数代表的位置出现了错误,纠错很简单直接进行位反转就行了,0转1,1转0
CRC
这个里面的核心算法是一个叫做模2除法的东西,这个东西应该是CRC中的核心部分了。
模2除法:
计算过程就是最高位够用就按照四则混合运算的除法在商位置写1,然后余数使用异或计算。
CRC的算法流程如下
根据多项式最高次项的系数进行移位,例如对于多项式移位补0后:进行模2除法被除数为信息码移位后结果101001000 除数为二进制展开1101
得到的余数就是CRC校验码,把这个CRC校验码写到后面就可以了,结果为101001001
校验过程是一个逆过程,对一个含有CRC的信息串通过模2除,计算余数,如果不全为0,则十进制数代表的位置的信息出现了错误,反转就可以了。

C语言实现CRC校验(多种方法)CRC(Cyclic Redundancy Check)校验应用较为广泛,以前为了处理简单,在程序中大多数采用LRC(Longitudinal Redundancy Check)校验,LRC校验很好理解,编程实现简单。
用了一天时间研究了CRC 的C语言实现,理解和掌握了基本原理和C语言编程。
结合自己的理解简单写下来。
1、CRC简介CRC检验的基本思想是利用线性编码理论,在发送端根据要传送的k位二进制码序列,以一定的规则产生一个检验码r位(就是CRC码),附在信息后面,构成一个新的二进制码序列数共(k+r)位,最后发送出去。
接收端根据同样的规则校验,以确定传送中是否出错。
接收端有两种处理方式:1、计算k位序列的CRC码,与接收到的CRC比较,一致则接收正确。
2、计算整个k+r位的CRC码,若为0,则接收正确。
CRC码有多种检验位数,8位、16位、32位等,原理相同。
16位的CRC码产生的规则是先将要发送的二进制序列数左移16位(即乘以2的16次方后),除以一个多项式,最后所得到的余数就是CRC 码。
求CRC码所采用的是模2运算法则,即多项式除法中采用不带借位的减法运算,运算等同于异或运算。
这一点要仔细理解,是编程的基础。
CRC-16: (美国二进制同步系统中采用) G(X) = X16 + X15 + X2 + 1CRC-CCITT: (由欧洲CCITT推荐) G(X) = X16 + X12 + X5 + 1CRC-32: G(X) = X32 + X26 + X23 + X22 + X16 +X12 + X11 + X10 + X8 + X7 + X5 + X4 + X2 + X1 + 12、按位计算CRC采用CRC-CCITT多项式,多项式为0x11021,C语言编程时,参与计算为0x1021,这个地方得深入思考才能体会其中的奥妙,分享一下我的思路:当按位计算CRC时,例如计算二进制序列为1001 1010 1010 1111时,将二进制序列数左移16位,即为1001 1010 1010 1111 (0000 0000 0000 0000),实际上该二进制序列可拆分为1000 0000 0000 0000 (0000 0000 0000 0000) + 000 0000 0000 0000 (0000 0000 0000 0000) + 00 0000 0000 0000 (0000 0000 0000 0000) + 1 0000 0000 0000 (0000 0000 0000 0000) + ……现在开始分析运算:<1>对第一个二进制分序列求余数,竖式除法即为0x10000 ^ 0x11021运算,后面的0位保留;<2>接着对第二个二进制分序列求余数,将第一步运算的余数*2后再和第二个二进制分序列一起对0x11021求余,这一步理解应该没什么问题。

CRC校验算法的分析及C语言实现CRC(循环冗余校验)是一种常见的校验算法,用于检测和纠正数据传输中的错误。
CRC校验算法通过生成多项式对发送的数据进行计算,并将校验结果附加到数据中进行传输。
接收方可以使用相同的多项式进行计算,并将结果与接收到的数据进行比较,以检查是否存在传输错误。
1.选择一个生成多项式,通常用一个16位或32位的二进制数表示。
2.将原始数据与补充的0进行异或操作,并左移一个单位。
3.重复上述步骤,直到向左移位的次数等于生成多项式的位数。
4.将得到的余数作为校验位,将其附加到原始数据后面。
5.接收方使用相同的生成多项式进行计算,并将计算得到的余数与接收到的数据进行比较。
如果两者不相等,则说明数据存在错误。
接下来,我们将使用C语言实现一个简单的CRC校验算法。
```c#include <stdio.h>#include <stdbool.h>unsigned long crc_table[256];//初始化CRC表void init_crc_tablunsigned long crc;int i, j;for (i = 0; i < 256; i++)crc = i;for (j = 8; j > 0; j--)if (crc & 1)crc = (crc >> 1) ^ POLYNOMIAL;elsecrc >>= 1;}crc_table[i] = crc;}//计算CRC值unsigned long crc32(unsigned char *message, int length) unsigned long crc = 0xfffffffful;int i;for (i = 0; i < length; i++)crc = (crc >> 8) ^ crc_table[(crc & 0xff) ^ message[i]]; return crc ^ 0xfffffffful;int maiint length = sizeof(message) - 1;init_crc_table(;unsigned long crc = crc32(message, length);printf("CRC32: %lx\n", crc);return 0;```上述代码中,我们首先定义了一个生成多项式POLYNOMIAL,并定义了一个包含256个元素的CRC表crc_table。
1.生成多项式。
16位的CRC码产生的规则是先将要发送的二进制序列数左移16位(既乘以)后,再除以一个多项式,最后所得到的余数既是CRC码。
任意一个由二进制位串组成的代码都可以和一个系数仅为…0‟和…1‟取值的多项式一一对应。
例如:代码1010111对应的多项式为x6+x4+x2+x+1,而多项式为x5+x3+x2+x+1对应的代码101111。
标准CRC生成多项式如下表:名称生成多项式简记式* 标准引用CRC-4 x4+x+1 3 ITU G.704CRC-8 x8+x5+x4+1 0x31CRC-8 x8+x2+x1+1 0x07CRC-8 x8+x6+x4+x3+x2+x1 0x5ECRC-12 x12+x11+x3+x+1 80FCRC-16 x16+x15+x2+1 8005 IBM SDLCCRC16-CCITT x16+x12+x5+1 1021 ISO HDLC, ITU X.25, V.34/V.41/V.42, PPP-FCSCRC-32 x32+x26+x23+...+x2+x+1 04C11DB7 ZIP, RAR, IEEE 802 LAN/FDDI, IEEE 1394, PPP-FCSCRC-32c x32+x28+x27+...+x8+x6+1 1EDC6F41 SCTP //叶子:这里不知道问什么省略了,有些迷惑哦。
要是生成多项式要是都省了,那还怎么校验?我猜想可能是中间的全为一吧。
生成多项式的最高位固定的1,故在简记式中忽略最高位1了,如0x1021实际是0x11021。
I、基本算法(人工笔算):以CRC16-CCITT为例进行说明,CRC校验码为16位,生成多项式17位。
假如数据流为4字节:BYTE[3]、BYTE[2]、BYTE[1]、BYTE[0];数据流左移16位,相当于扩大256×256倍,再除以生成多项式0x11021,做不借位的除法运算(相当于按位异或),所得的余数就是CRC校验码。
CRC校验原理及步骤标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]CRC校验原理及步骤什么是CRC校验CRC即循环冗余校验码:是数据通信领域中最常用的一种查错校验码,其特征是信息字段和校验字段的长度可以任意选定。
循环冗余检查(CRC)是一种数据传输检错功能,对数据进行多项式计算,并将得到的结果附在帧的后面,接收设备也执行类似的算法,以保证数据传输的正确性和完整性。
CRC校验原理:其根本思想就是先在要发送的帧后面附加一个数(这个就是用来校验的校验码,但要注意,这里的数也是二进制序列的,下同),生成一个新帧发送给接收端。
当然,这个附加的数不是随意的,它要使所生成的新帧能与发送端和接收端共同选定的某个特定数整除(注意,这里不是直接采用二进制除法,而是采用一种称之为“模2除法”)。
到达接收端后,再把接收到的新帧除以(同样采用“模2除法”)这个选定的除数。
因为在发送端发送数据帧之前就已通过附加一个数,做了“去余”处理(也就已经能整除了),所以结果应该是没有余数。
如果有余数,则表明该帧在传输过程中出现了差错。
模2除法:模2除法与算术除法类似,但每一位除的结果不影响其它位,即不向上一位借位,所以实际上就是异或。
在循环冗余校验码(CRC)的计算中有应用到模2除法。
例:CRC校验步骤:CRC校验中有两个关键点,一是预先确定一个发送送端和接收端都用来作为除数的二进制比特串(或多项式),可以随机选择,也可以使用国际标准,但是最高位和最低位必须为1;二是把原始帧与上面计算出的除数进行模2除法运算,计算出CRC码。
具体步骤:1. 选择合适的除数2. 看选定除数的二进制位数,然后再要发送的数据帧上面加上这个位数-1位的0,然后用新生成的帧以模2除法的方式除上面的除数,得到的余数就是该帧的CRC校验码。
注意,余数的位数一定只比除数位数少一位,也就是CRC校验码位数比除数位数少一位,如果前面位是0也不能省略。
crc校验算法案例CRC校验算法是一种常用的数据校验方法,它通过计算数据的校验值来检测数据传输过程中是否发生了错误。
在本文中,我们将以实际案例的形式介绍CRC校验算法的原理、应用和实现。
案例1:通信传输中的CRC校验假设某个通信系统中,发送端需要将一段数据通过信道传输给接收端,为了保证数据的可靠性,发送端在数据末尾添加了一个CRC校验码。
接收端在接收到数据后,会对接收到的数据进行CRC校验,以确定数据是否传输正确。
如果校验结果与接收到的CRC校验码一致,则认为数据传输正确,否则认为数据传输发生错误。
案例2:计算机存储中的CRC校验在计算机存储中,CRC校验也被广泛应用。
例如,在硬盘中存储的数据经常会受到磁头的干扰,导致数据发生位错误。
为了保证数据的可靠性,硬盘会在存储数据时,为每个数据块计算并存储一个CRC校验码。
在读取数据时,硬盘会重新计算数据的CRC校验码,并与存储的校验码进行比较,以确定数据是否发生了位错误。
案例3:网络通信中的CRC校验在网络通信中,CRC校验算法被广泛应用于数据包的传输。
例如,在以太网中,每个数据包都会附带一个CRC校验码,在接收端对数据包进行校验时,会重新计算数据的CRC校验码,并与接收到的校验码进行比较,以确定数据是否传输正确。
案例4:无线通信中的CRC校验在无线通信中,由于信道的不稳定性,数据传输往往会受到干扰,导致数据错误。
为了保证数据的可靠性,无线通信系统常常会使用CRC校验算法对数据进行校验。
发送端在发送数据时,会计算数据的CRC校验码并附加在数据中,接收端在接收数据时,会对接收到的数据进行CRC校验,以确定数据是否传输正确。
案例5:存储介质中的CRC校验在存储介质中,如磁带、光盘等,数据的可靠性是非常重要的。
为了保证数据的可靠性,这些存储介质会使用CRC校验算法对存储的数据进行校验。
在读取数据时,存储介质会计算数据的CRC校验码,并与存储的校验码进行比较,以确定数据是否发生了错误。
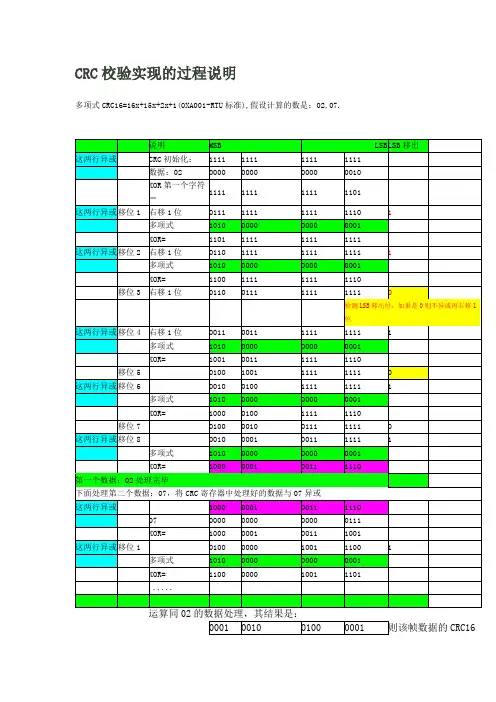
CRC校验专题以CRC-16为例,说明CRC的计算过程:1.设置CRC寄存器,并给其赋值FFFF(hex)。
2.将数据的第一个8-bit字符与16位CRC寄存器的低8位进行异或,并把结果存入CRC寄存器。
3.CRC寄存器向右移一位,MSB补零,移出并检查LSB。
4.如果LSB为0,重复第三步;若LSB为1,CRC寄存器与多项式码相异或。
5.重复第3与第4步直到8次移位全部完成。
此时一个8-bit数据处理完毕。
6.重复第2至第5步直到所有数据全部处理完成。
7.最终CRC寄存器的内容即为CRC值。
翻译:1.意思是首先寄存器中的值是11111111111111112.数据第一个字节一个字节=8位用二进制表示就是【00000000-11111111】之间用这个数值跟寄存器中的16个1中的后8位进行异或(异或不知道什么意思的自己查简单理解就是同为0 异为1)然后把这个数值保存到寄存器中3.判断最后一位是否为0 如果为0寄存器中的值向右移动一位前面补零如果为1 拿寄存器中的值与多项式进行异或。
4.检查当前寄存器中的最后一位如果是0 重复第三步;如果是寄存器中的值与多项式进行异或5.重复3与4直到8此移位完成。
6.重复第2到第五步知道正规数组的数据验证完成7.最终计算出的就是CRC的值实例:实例byte[] bufs=new byte[]{0x2f,0x12,0x31} crc16 多项式码假设是0x8408 二进制形式就是10000100000010001crc=0xffff; 用二进制表示就是11111111111111112拿出bufs中第一个字节0x2f 二进制表示00101111 跟寄存器中的后8位进行异或得到11111111110100003判断CRC寄存器中最后一位当前为0 寄存器右移一位得到0111111111101000 (如果为1就与多项式进行异或)4判断当前寄存器中的值当前最后一位为0 所以重复第三步继续右移得到0011111111110100 最后还是0 在重复第三步0001111111111010 最后还是0 继续第三步0000111111111101 这时最后一位为1了这时与多项式进行异或得到10111011111110015重复判断知道判断完8次6然后再重复第2到第5步直到上面数组中的bufs中三个字节验证完7最终寄存器中的值就是crc值下面进行实战C# code 分析const uint PRESET_VALUE = 0xFFFF; 初始化寄存器的值const uint POLYNOMIAL = 0x8408; 多项式码三个参数 1char数组 byte一样 2.数组长度uint uiCrc16Cal(char[] pucY, int ucX){uint ucI, ucJ;uint uiCrcValue = PRESET_VALUE; 赋除值for(ucI = 0; ucI < ucX; ucI++){uiCrcValue = uiCrcValue ^ pucY[ucI]; 进行异或for(ucJ = 0; ucJ < 8; ucJ++) 由于一个字节 8位所以判段8次{if((uiCrcValue & 0x0001) != 0) (*1下面解释){uiCrcValue = (uiCrcValue >> 1) ^ POLYNOMIAL;} (*2下面解释)else{uiCrcValue = (uiCrcValue >> 1);} (*3下面解释)}}return uiCrcValue;}*1 “&”这个符号在C 、C#等语言上是按位与即按二进制比对1与1 得1 0与1得0 0与0得0 例如:比如:10010001(二进制)&11110000等于10010000(二进制)。
单片机 crc32程序CRC32(循环冗余校验)是一种广泛用于数据传输和存储中的校验方法,它可以检测数据是否在传输或存储过程中发生了错误。
在单片机中实现CRC32校验算法可以通过软件实现,也可以通过硬件加速实现。
这里我将为你提供一个基于软件的CRC32算法的示例程序,该程序可以在单片机上运行。
c.#include <stdio.h>。
#include <stdint.h>。
#define POLYNOMIAL 0xEDB88320L.uint32_t crc32(uint8_t data, uint32_t length) {。
uint32_t crc = 0xFFFFFFFF;for (uint32_t i = 0; i < length; i++) {。
crc = crc ^ data[i];for (uint32_t j = 8; j > 0; j--) {。
if (crc & 1) {。
crc = (crc >> 1) ^ POLYNOMIAL; } else {。
crc = crc >> 1;}。
}。
}。
return crc ^ 0xFFFFFFFF;}。
int main() {。
uint8_t test_data[] = {0x01, 0x02, 0x03, 0x04,0x05};uint32_t crc = crc32(test_data, 5);printf("CRC32: 0x%08X\n", crc);return 0;}。
在这个示例程序中,我们使用了一个名为`crc32`的函数来计算CRC32校验值。
该函数接受一个`uint8_t`类型的数据指针和数据长度作为输入,并返回计算得到的CRC32校验值。
在`main`函数中,我们提供了一个测试数据`test_data`,并调用`crc32`函数来计算CRC32校验值,最后将结果打印输出。
CRC码计算及校验原理计算
CRC(Cyclic Redundancy Check)码是一种常用的错误检测码,用于验证数据在传输过程中是否发生错误。
CRC码的计算和校验原理是通过生成多项式对数据进行计算和校验。
以下是CRC码计算及校验原理的详细解释。
一、CRC码的计算原理:
1.选择一个生成多项式G(x),比如G(x)=x^3+x^2+1
2.假设要发送的数据为D(x),将D(x)乘以x的次数等于生成多项式的次数再取模,得到一个除数。
3.将除数与G(x)进行异或运算,产生余数。
4.将余数拼接到原始数据D(x)的后面,得到新的数据N(x)。
5.将数据N(x)进行发送。
二、CRC码的校验原理:
1.接收到数据N(x)后,用生成多项式G(x)去除以接收的数据N(x)。
2.如果除数为0,则认为数据没有发生错误,否则则认为数据发生了错误。
举例说明:
1.计算步骤:
2.校验步骤:
-用生成多项式G(x)去除以接收的数据N(x),得到商和余数。
-如果余数为0,说明数据没有发生错误,否则说明数据发生了错误。
通过以上计算和校验步骤,可以判断数据在传输过程中是否发生错误。
CRC码的优点是简单、效率高,能够检测到大部分错误,被广泛应用
在通信、存储等领域。
然而,CRC码只能检测错误,不能纠正错误。
当数
据发生错误时,需要重新发送数据或通过其他方法进行纠错处理。