武汉大学刘觉平群论第十一次作业

物理学中的群论——群论基础主讲翦知渐群论教材教材与参考书教材：自编参考书群论及其在固体物理中的应用参考书：群论及其在固体物理中的应用（徐婉棠）物理学中的群论（马中骐）物理学中的群论基础（约什）群论-群论基础第章群论基础第一章群的基本概念和基本性质§1.1 集合与运算§1.2群的定义和基本性质§1.3 子群及其陪集13§1.4 群的共轭元素类§1.5 正规子群和商群§1.6 直积和半直积16§1.7 对称群§1.8 置换群§1.1集合与运算抽象代数的基本概念1集合抽象代数研究的对象什么都不是，所以什么都是集合的直乘：C=A×B，表示“C的元素是由A和B两个集合的元素构成的C A表示“一对有序元”，也称为A和B的直乘，用符号表示即：, a2,…, a i,…}，B={b1, b2,…, b j,…}，则集合设A={aA}B b b}则集合1C=A×B={(a i,b j)| a i∈A, b j∈B}是A与B的直乘。

定义设是两个集合若有种规则使得2映射定义：设A 与B 是两个集合，若有一种规则f ，使得A 的每一个元素在B 上都有唯一的元素与之对应，这种对应规则f 的一个映射记为就称为A 到B 的个映射，记为f ：A → Bf ：x → y = f ( x ) , 或写为f y f (),式中y 称为x 在B 上的象，而x 称为y 在A 上的原象。

对应规则函数对应规则：函数满射单射一一映射逆映射：f -1恒等映射：e 变换恒等映射：体系A 的一个自身映射f 称为A 的一个变换，若f 是一一映射则称为对称变换一一变换有性质：射，则称为对称变换。

变换有性质：f f -1= f -1f = e3二元运算定义：若对A 上的每对有序元(a, b ) ，在A 上有唯确定的A每一对a,b)A上有唯一确定的c与之对应，即有一规则R 使得A×A → A，则R 称为A上的一个二元运算，记为()()R：A×A → A，或R：a, b ) →c= R(a, b)一般记为c = a·b，或c = ab。

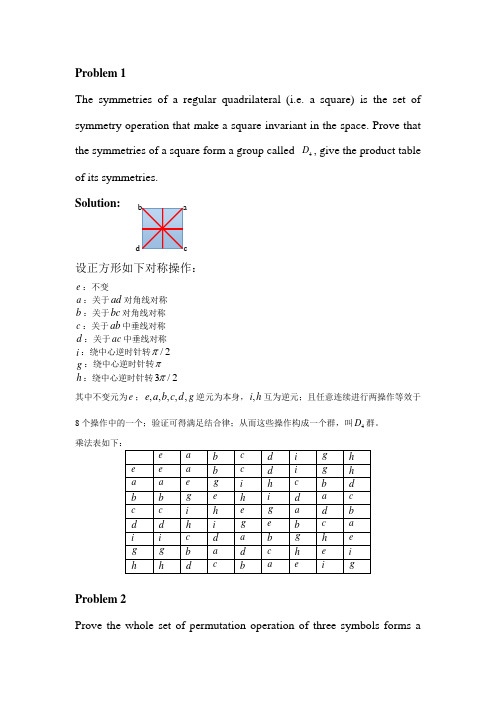
Problem 1The symmetries of a regular quadrilateral (i.e. a square) is the set of symmetry operation that make a square invariant in the space. Prove that the symmetries of a square form a group called 4D , give the product table of its symmetries. Solution:设正方形如下对称操作：e ：不变a ：关于ad 对角线对称b ：关于bc 对角线对称 c ：关于ab 中垂线对称d ：关于ac 中垂线对称 i ：绕中心逆时针转/2π g ：绕中心逆时针转π h ：绕中心逆时针转3/2π其中不变元为e ；,,,,,e a b c d g 逆元为本身，,i h 互为逆元；且任意连续进行两操作等效于8个操作中的一个；验证可得满足结合律；从而这些操作构成一个群，叫4D 群。

乘法表如下：e a b c d i g h e e a b cd igh aaegi h cbdbbgehi daccci h egadbd d hi geb ca i i cdabgheggb a dc hei hhdc baeigProblem 2Prove the whole set of permutation operation of three symbols forms ad bcagroup 3S ，and prove it is isomorphic to the group 3D , the set of symmetries of an equilateral triangle. Solution:所有置换操作为：123123123123123123=,=,=,=,=,=123132213231312321e a b c d g ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭经验算满足群的性质，从而构成所谓的3S 群，且其乘法表如下：e a b c d g e e a b c d gaae dgb cbbceagdccb gde addga ec bg gdcbae与3D 群的乘法表对照知，此两群同构Problem 3. Show that the set of non-zero complex numbers,under the usual multiplication,is a group. Solution:设非零复数12=+a a a i ，12b b b i =+，12c c c i =+属于非零复数集。

群论课后习题答案群论是数学中的一个分支，研究的是群的性质和结构。

在学习群论的过程中，习题是不可或缺的一部分，通过解答习题可以加深对群论概念和定理的理解。

本文将给出一些群论课后习题的答案，希望能对读者在学习群论时有所帮助。

1. 证明：对于任意群G和H，如果存在同构映射f: G→H，则G和H具有相同的群性质。

证明：假设f: G→H是一个同构映射。

由同构的定义可知，f是一个双射，并且满足对于任意的g1, g2∈G，有f(g1g2) = f(g1)f(g2)。

首先证明G和H具有相同的单位元。

设eG和eH分别是G和H的单位元，则有f(eG) = eH。

对于任意的h∈H，存在g = f^(-1)(h)∈G，因此有f(g) = h。

由此可得f(eG) = f(geG) = f(g)f(eG) = hf(eG)，即eH = hf(eG)。

同理可证hf(eG) = eH，因此G和H具有相同的单位元。

其次证明G和H具有相同的逆元。

设g∈G，对应的元素f(g)∈H。

由于f是双射，存在g' = f^(-1)(f(g))∈G，使得f(g') = f(g)^(-1)。

因此有f(g)f(g') = f(gg') = eH。

同理可证f(g')f(g) = eH。

由此可知g' = g^(-1)，即G和H具有相同的逆元。

最后证明G和H具有相同的封闭性。

设g1, g2∈G，对应的元素f(g1), f(g2)∈H。

由于f是双射，存在g' = f^(-1)(f(g1)f(g2))∈G，使得f(g') = f(g1g2)。

因此有f(g') = f(g1)f(g2)。

由此可知g' = g1g2，即G和H具有相同的封闭性。

综上所述，如果存在同构映射f: G→H，则G和H具有相同的群性质。

2. 设G是一个有限群，证明：G的任意子群的阶数必整除G的阶数。

证明：设H是G的一个子群，记|G|为G的阶数，|H|为H的阶数。

第一篇：武汉大学工程硕士《自然辩证法》复习思考题(1)武汉大学工程硕士《自然辩证法》复习思考题（2011年下半年~2012年上半年）教材：《自然辩证法——在工程中的理论与应用》（清华大学出版社）导论：1、自然辩证法创立的自然科学成果。

2、工程硕士学习自然辩证法的意义。

第一章：1、科学、技术、工程及其基本特征。

2、科学、技术、工程的区别与联系。

3、如何认识发现、发明和建造三者之间的关系？第二章：1、现代自然科学的全面发展。

2、近代技术的发展。

3、如何认识现代科学、技术与工程的一体化发展趋势？第三章：1、何谓“系统”？2、自然界演化的自组织机制。

3、人与自然的对象性关系。

第四章：1、自然价值与自然权利。

2、生态伦理的原则和态度。

3、环境友好型社会。

第五章：1、创新概念包括哪些要素？它与企业家有何关系？2、创新对科学技术的依赖性。

3、科学技术、社会需求与创新。

4、企业的创新战略。

第六章：1、国家竞争力与国家创新体系建设。

2、自主创新战略及其意义。

3、新时期我国国家创新体系建设的主要任务体现在哪些方面？第七章：1、现代科学方法论及其形成。

2、科学问题及其来源。

3、观察和实验中的机遇。

4、举例说明归纳与演绎方法在科学研究中的作用。

第八章：1、工程技术研究的主要阶段。

2、利用专利文献的发明创造。

3、系统科学思想和方法的主要特点。

第九章：1、工程共同体的含义及类型。

2、科学和技术的社会规范。

第十章：1、工程技术共同体的伦理原则。

2、工程师的社会责任。

3、工程技术活动中越轨行为及其控制。

第十一章：1、科学技术工程对人类社会的影响。

2、文化对科学、技术和工程的影响。

第十二章：1、如何正确评价“技术乐观主义”和“技术悲观主义”？2、科学、技术、工程社会评价的主要原则。

考试形式：开卷考试题型：辨析题、简答题、论述题（包括材料题）武汉大学研究生院2011年7月第二篇：武汉大学工程硕士《自然辩证法》复习思考题武汉大学工程硕士《自然辩证法》复习思考题（2010年下半年~2011年上半年）教材：《自然辩证法——在工程中的理论与应用》（清华大学出版社）导论：1、自然辩证法创立的自然科学成果。

第十二章 群论简介习题§12.1 群的定义和例子１．设Ｇ为一切不等于零的有理数所成的集合，证明Ｇ对于数的乘法作成一个群． 【证明】１）任意两个非零的有理数的乘积为非零有理数，故Ｇ对数的乘法封闭；２）数的乘法结合律对一切数都成立，自然对Ｇ也成立； ３）01≠是非零有理数，且对任何一个非零有理数a ，011≠=⨯=⨯a a a ， 说明１是Ｇ的单位元素； ４）对任意的非零有理数a ，则a1是非零有理数，且 111=⨯=⨯a aa a ， 说明a 的逆元是a 1，根据群的定义，即知集合Ｇ对数的乘法作成一个群． ２．Ｇ是由a ，b ，c 三个元素所作成的集合，它的乘法表是判别Ｇ是否成群？【解】由乘法表容易看到，Ｇ对规定的乘法是封闭的，a 是Ｇ的单位元素，a 、b 、c 的逆元分别是a 、c 、b ． 以下只要证明结合律成立即可．因为(ab)c ＝bc ＝a ，a(bc)＝aa ＝a ，故(ab)c ＝a(bc)；同法可知a(cb)＝(ac)b ＝a ，(ba)c ＝b(ac)＝a ，(bc)a ＝b(ca)＝a ，(ca)b ＝c(ab)＝a ，(cb)a ＝c(ba)＝a ，以上６个式子说明结合律对规定的乘法是成立的， 因此Ｇ对规定的乘法作成一个群．３．证明下列四个方阵Ａ，Ｂ，Ｃ，Ｄ对于矩阵乘法作成一个群Ｖ，写出的Ｖ乘法表．Ｖ是否循环群？Ｖ是否交换群？⎪⎪⎭⎫ ⎝⎛=1001A ，⎪⎪⎭⎫ ⎝⎛-=1001B ，⎪⎪⎭⎫ ⎝⎛-=1001C ，⎪⎪⎭⎫⎝⎛--=1001D ．【证明】先写出乘法表．由乘法表看出，集合Ｖ＝｛Ａ，Ｂ，Ｃ，Ｄ｝对矩阵乘法封闭，结合律对任何矩阵的乘法满足，自然对Ｖ中的矩阵也满足，而矩阵Ａ是单位元，元素Ａ、Ｂ、Ｃ、Ｄ的逆元素分别是它们自身，故Ｖ对矩阵的乘法作成群． 但（Ａ）＝｛Ａ｝，（Ｂ）＝｛Ａ，Ｂ｝，（Ｃ）＝｛Ａ，Ｃ｝，（Ｄ）＝｛Ａ，Ｄ｝， 它们都不等于Ｖ，从而Ｖ不是循环群．由乘法表的对称性，可知群Ｖ是一个交换群．§12.2 置换群１．求置换的乘积：⎪⎪⎭⎫⎝⎛2451354321⎪⎪⎭⎫ ⎝⎛1543254321 【解】⎪⎪⎭⎫⎝⎛2451354321⎪⎪⎭⎫ ⎝⎛1543254321⎪⎪⎭⎫ ⎝⎛=3245115432⎪⎪⎭⎫ ⎝⎛1543254321 ⎪⎪⎭⎫⎝⎛=3245154321． ２．把置换表为轮换的乘积： （１）⎪⎪⎭⎫⎝⎛12765437654321， 【解】⎪⎪⎭⎫⎝⎛12765437654321)642)(7531(=； （２）⎪⎪⎭⎫⎝⎛1234568787654321． 【解】⎪⎪⎭⎫ ⎝⎛1234568787654321)54)(63)(8271(=．３．证明：（１）121)(-k i i i )(11i i i k k -=；（２）设Ｐ，Ｑ为两个不相交的轮换，则ＰＱ＝ＱＰ．【证明】（１）)(21k i i i ⎪⎪⎭⎫⎝⎛=++n k n k k i i i i ii i i i i 1132121,)(11i i i k k -⎪⎪⎭⎫⎝⎛=+--+-n k kk k n k k k i i i i ii i i i i 121111, )(11i i i k k -)(21k i i i⎪⎪⎭⎫ ⎝⎛=+--+-n k k k k n k k k i i i i ii i i i i 121111⎪⎪⎭⎫⎝⎛++n k n k ki i i i i i i i i i 1132121⎪⎪⎭⎫ ⎝⎛=++n k k n k i i i i i i i i i i 1211132⎪⎪⎭⎫⎝⎛++n k n k ki i i i i i i i i i 1132121)(1121121i i i i i i i i i i i n k kn k k =⎪⎪⎭⎫⎝⎛=++ ,（恒等变换）同理可证 )(21k i i i )(11i i i k k -)(1i =，所以 121)(-k i i i )(11i i i k k -=．（２）设)(21k i i i P =⎪⎪⎭⎫⎝⎛=++++n r rk n r r k k i i i i i i ii i i i i i i 111321121，)(21r k k i i i Q ++=⎪⎪⎭⎫⎝⎛=+++++n r k k k n r r k k i i i i i i ii i i i i i i 112211121， 其中没有相同的数字．则 )(21k i i i PQ =)(21r k k i i i ++⎪⎪⎭⎫⎝⎛=+++++n r k k n r r k k i i i i i i i i i i i i i i 1121321121)(21r k k i i i ++=QP i i i k =)(21 .４．写出四次对称群的所有置换．【解】四次对称群的全体置换（共２４个）用轮换的形式表示就是： （１）； （１２），（１３），（１４），（２３），（２４），（３４）； （１２３），（１３２），（１３４），（１４３），（１２４），（１４２），（２３４），（２４３）； （１２３４），（１２４３），（１３２４），（１３４２），（１４２３）（１４３２）； （１２）（３４），（１３）（２４），（１４）（２３）．§12.3 子群及其陪集１．求出三次对称群的所有子群．【解】)}132(),123(),23(),13(),12(),1{(3=S ，它的平凡子群为单位元群)}1{(及3S 本身；其２阶子群有３个，即)}12(),1{(1=H ，)}13(),1{(2=H ，)}23(),1{(3=H ； 三阶子群只有１个，即)}132(),123(),1{(4=H ，由拉格朗日定理，不可能有其它阶数的真子群，因此以上所列就是3S 的所有子群．２．证明：阶为质数的群一定是循环群．【证明】设Ｇ群的阶为质数p ，则Ｇ必含有周期大于１的元素，不妨设为a ，其周期为m ＞１，故由a 生成的循环群（a ）是群Ｇ的子群，其阶数为m ， 由拉格朗日定理知，m 整除p ， 但p 是质数，故m ＝p ， 从而 Ｇ＝（a ），即Ｇ是循环群． ３．证明：阶为质数幂mp 的群中包含一个阶为p 的子群．【证明】设群Ｇ的阶为mp ，因p 为质数，故群Ｇ含有非单位元素a ． 设a 的周期为n ，由拉格朗日定理的推论，知n 整除mp ，即rn p =，1r m ≤≤． 若r ＝１，则循环群（a ）＝2{,,,}p a a a e =是Ｇ的p 阶子群；若1r >，那么循环群（1r p a-）＝1112{,,,}---==r r r rp p pp p a a a a e是Ｇ的p 阶子群．证完．４．证明：循环群的子群也是循环群． 【证明】设Ｇ是循环群，Ｈ是其子群．若Ｇ是单位元群，则显然Ｈ＝Ｇ，故结论成立． 下面讨论Ｇ不是单位元群的情况． 若Ｇ＝（ａ），其中ａ不是单位元，Ｈ是Ｇ的子群，但不是单位元群，那么Ｈ中必含有m ＞０的幂ma ．不妨就设m a 是Ｈ中a 的最小正幂，显然Ｈ包含ma 的任何乘幂． 若sa 是Ｈ中的任意元素，由s ＝tm ＋r ，m r <≤0，可知 t m s tms ra a aa --==)( 也是Ｈ中的元素，但m 是最小正整数，而且m r <≤0，故r ＝０， 于是 tmsa a )(=，这就是说，Ｈ中的任意元素s a 都是m a 的幂，即Ｈ只含有ma 的任意乘幂， 所以Ｈ是由m a 生成的循环群，即Ｈ＝（ma ）． 这样就证明了命题．５．证明：群Ｇ的一个元素a 是恒等元的充分必要条件为a 适合关系a a =2． 【证明】必要性是显然的．下面只证充分性．设群Ｇ的恒等元为e ，由于e a a aa==--11，在关系式a a =2两端同时乘a 的逆元1-a ，有e aa aa ==--112而 a ae aa a aa ===--)(112，所以 e a =，即a 是群Ｇ的单位元．§12.4 共轭类与子群１．设⎪⎪⎭⎫ ⎝⎛=2145354321P ，⎪⎪⎭⎫ ⎝⎛=5143254321Q ，求1-QPQ ．【解】使用教材８４—８５页的方法，对置换Ｐ的上下两行分别施行置换Ｑ，得 1-QPQ⎪⎪⎭⎫ ⎝⎛=3215451432⎪⎪⎭⎫ ⎝⎛=3154254321． ２．设四阶群Ｖ＝｛ｅ，ａ，ｂ，ｃ｝的乘法表为求出Ｖ的所有共轭类．【解】由Ｖ的乘法表看出，群Ｖ是可换群，故群Ｖ的每一个元素就是一个共轭类．即群Ｖ有四个共轭类：｛ｅ｝，｛ａ｝，｛ｂ｝，｛ｃ｝． ３．证明：指数为２的子群一定是正规子群．【证明】设Ｈ为群Ｇ的子群，由于［Ｇ：Ｈ］＝２，则群Ｇ按子群Ｈ的左分解为Ｇ＝Ｈ＋ａＨ按Ｈ的右分解为 Ｇ＝Ｈ＋Ｈａ， 其中H a ∉． 因此 ａＨ＝Ｈａ，即对任意的H a ∉，都有 H aHa =-1．若H a ∈，则ａＨ＝Ｈａ，即H aHa=-1显然成立．依正规子群的定义，Ｈ是正规子群． ４．证明：交换群的每一个子群都是正规子群．【证明】设Ｇ为交换群，Ｈ为Ｇ的子群，则对任意的G a ∈，都有ａＨ＝Ｈａ，即H aHa=-1，所以Ｈ是正规子群．５．求四次对称群的所有共轭类．【解】由§１２．２的习题４，知4S 的所有置换（共２４个）为（１）； （１２），（１３），（１４），（２３），（２４），（３４）； （１２３），（１３２），（１３４），（１４３），（１２４），（１４２），（２３４），（２４３）； （１２３４），（１２４３），（１３２４），（１３４２），（１４２３）（１４３２）； （１２）（３４），（１３）（２４），（１４）（２３）． 再由教材８５页的定理２，具有相同的轮换结构的置换必共轭，知4S 共有５个共轭类， 即上面的每一行的置换组成一个共轭类．§12.5 点群１．证明：点群3D 含有三个共轭类．【证明】点群3D 有一个三重轴（取为z 轴）及三条二重轴（与z 轴垂直），其元素为)3(2)2(2)1(2233,,,,,C C C C C E ，其中23)()3(23)()2(2)()1(2,,C C C C C yz v yz v yz v σσσ===,这个群的乘法表为233,C C 属于一个共轭类．这是因为233,C C 有共同的旋转轴，而变换Ｅ即保持它不变． (1)(2)(3)222,,C C C 属于另一个共轭类．因为只要作变换3C 或23C ，反映(1)(2)(3)222,,C C C 的对称平面即可互相转化．而Ｅ是恒等变换，它单独成一类． 所以两面体群3D 共有三个共轭类． ２．求出点群ℭh 3的元素和它的乘法表．【解】把反映h σ加到旋转群2333(){,,}C E C C =上去，并用h σ分别乘233,C C ，即得点群ℭh 3223333{,,,,,}h h h E C C C C σσσ=．它的乘法表为注意上述乘法表使用了可换性．３．设I 为以原点为对称中心的反演，证明2G ＝},{I E 是一个群． 【证明】写出2G 的乘法表 则显然2G 是一个群．§12．6 同构对应和同态对应１．证明：三次对称群3S 与点群两面体群3D 同构． 【证明】三次对称群3S 元素为Ｅ＝（１），Ａ＝（１２），Ｂ＝（１３），Ｃ＝（２３），Ｄ＝（１２３），Ｆ＝（１３２）． 其乘法表为而3D 的乘法表为（上节习题１）：作从对应3S 到3D 的对应ϕ：(1)(2)(3)222233,,,,,E E A C B C C C D C F C →→→→→→，比较两个群，发现它们有共同的乘法表，故3S 与3D 同构． ２．证明：点群v G 2与点群h G 2同构．【证明】点群v G 2＝()()()2{,,,}z xz yz v v E C σσ与点群h G 2＝22{,,,}h h E C C σσ，它们的乘法表分别为22h h E C σσ C E 22h h E C σσ C 2C h h σσ22C E C h σ 22C σσh h C E 2h C σ 2h σσ2h C C E作两个群之间的对应ϕ：()()()222,,z xz yz v h v h E E C C C σσσσ→→→→，则由两个群的乘法表可知，ϕ是一个同构对应， 从而点群v G 2与点群h G 2同构．３．证明：点群v G 3与下面的矩阵乘群M 同构．⎪⎪⎭⎫ ⎝⎛=10011A ，⎪⎪⎪⎪⎭⎫ ⎝⎛---=212323212A ，⎪⎪⎪⎪⎭⎫ ⎝⎛---=212323213A ， ⎪⎪⎭⎫ ⎝⎛-=10014A ，⎪⎪⎪⎪⎭⎫ ⎝⎛---=212323215A ，⎪⎪⎪⎪⎭⎫ ⎝⎛-=212323216A ． 【证明】v G 3的乘法表参见教材９２页．作矩阵乘群的乘法表，作v G 3与矩阵乘群M 之间的一一对应ϕ：2(1)(2)(3)13233456,,,,,v v v E A C A C A A A A σσσ→→→→→→比较它们的乘法表，知v G 3与矩阵乘群M 同构．４．证明：群Ｇ的子群Ｈ与每一个左陪集ａＨ之间存在１—１对应． 【证明】假如{}H h =，则{|,}aH ah a G h H =∈∈．下面分两种情况讨论． １）a H ∈的情形，此时有aH H =，则Ｈ的元素与自身的对应（即恒等对应）就是一个一一对应； ２）a H ∉的情形，作Ｈ到ａＨ的对应:h ah ϕ→，则可证ϕ是一一对应．事实上，对Ｈ中不同的元素12,h h ，则它们的象12ah ah ≠，否则将会有12h h =， 这说明不同元素的象也不同，即ϕ是一个单射；另一方面，如果ah 是aH 的一个元素，则按aH 的定义，即知ｈ是ａｈ的一个原象，这说明ϕ是从Ｈ到ａＨ上的对应，即ϕ是一个满射， 从而ϕ是一一对应．综上所述，Ｈ与ａＨ之间存在１—１对应． ５．证明：存在一个从点群v G 2到点群2G 上的同态对应． 【证明】点群v G 2和点群2G 的乘法表分别是作对应()()()222:*,,,z xz yz v v E E C E C C ϕσσ→→→→，则(#)(#)*(#)()(#)E E E ϕϕϕϕϕ===，＃表示()()()2z xz yz v v C σσ,,中的任意一个变换．()()()()()2222()()*()()z xz yz z xz v v v C C E C C ϕσϕσϕϕσ====， ()()()()()2222()()*()()z yz xz z yz v v v C C E C C ϕσϕσϕϕσ====，()()()()22()()*()()xz yz xz yz v v v v E E C C ϕσσϕϕσϕσ====，注意到两个群都是交换群，故ϕ是从点群v G 2到点群2G 的一个同态对应．６．证明：除同构对应外，只有两个四阶群． 【证明】设四阶群Ｇ＝｛ｅ，ａ，ｂ，ｃ｝，则由拉格朗日定理的推论，即知群的元素的周期只能是１或２或４， 但a ，b ，c 的周期不能是１，故它们的周期必为２或４．１） 若a ，b ，c 之中有一个元素（比如说a ）的周期为４，则Ｇ＝（ａ），此时Ｇ为四阶循环群．２） 若a ，b ，c 的周期都是２，则Ｇ的乘法表一定是这是因为a ，b ，c 的周期为２，则222a b c e ===，而ab e ≠，否则，将有2e ab a b a ==⇒=，这与群的阶数为４不符； ab a ≠，否则b ＝e ，同样ab b ≠，这样只有ab c =．表中其它乘积的结果类似．因此，从同构的意义上说，只有两个四阶群，前一个是四阶循环群，后一个是Klein 四元群，它们都是交换群．。