自控原理实验3
- 格式:doc
- 大小:258.00 KB
- 文档页数:6

自动控制原理实验报告实验目的,通过本次实验,掌握自动控制原理的基本概念和实验操作方法,加深对自动控制原理的理解和应用。
实验仪器与设备,本次实验所需仪器设备包括PID控制器、温度传感器、电磁阀、水槽、水泵等。
实验原理,PID控制器是一种广泛应用的自动控制设备,它通过对比设定值和实际值,根据比例、积分、微分三个控制参数对控制对象进行调节,以实现对控制对象的精确控制。
实验步骤:1. 将温度传感器插入水槽中,保证传感器与水温充分接触;2. 将水泵接通,使水槽内的水开始循环;3. 设置PID控制器的参数,包括比例系数、积分时间、微分时间等;4. 通过调节PID控制器的参数,使得水槽中的水温稳定在设定的目标温度;5. 观察记录PID控制器的输出信号和水温的变化情况;6. 分析实验结果,总结PID控制器的控制特性。
实验结果与分析:经过实验操作,我们成功地将水槽中的水温控制在了设定的目标温度范围内。
在调节PID控制器参数的过程中,我们发现比例系数的调节对控制效果有着明显的影响,适当增大比例系数可以缩小温度偏差,但过大的比例系数也会导致控制系统的超调现象;积分时间的调节可以消除静差,但过大的积分时间会导致控制系统的超调和振荡;微分时间的调节可以抑制控制系统的振荡,但过大的微分时间也会使控制系统的响应变慢。
结论:通过本次实验,我们深入理解了PID控制器的工作原理和调节方法,掌握了自动控制原理的基本概念和实验操作方法。
我们通过实验操作和数据分析,加深了对自动控制原理的理解和应用。
总结:自动控制原理是现代控制工程中的重要内容,PID控制器作为一种经典的控制方法,具有广泛的应用前景。
通过本次实验,我们不仅学习了自动控制原理的基本知识,还掌握了PID控制器的调节方法和控制特性。
这对我们今后的学习和工作都具有重要的意义。

自动控制原理实验报告目录2.2典型环节模拟电路及其数学模型1. 实验目的2. 实验原理3. 实验内容4. 实验步骤5. 实验数据记录3.1典型二阶系统模拟电路及其动态性能分析1. 实验目的2. 实验原理3. 实验内容4. 实验步骤5. 实验数据纪录3.4三阶控制系统的稳定性分析1. 实验目的2. 实验原理3. 实验内容4. 实验步骤5. 实验数据记录3.5基于Matlab告诫控制系统的时域响应动态性能分析1. 实验目的2. 实验内容3. 实验数据纪录4.1基于Matlab控制系统的根轨迹及其性能分析1. 实验目的2. 实验原理3. 实验内容4. 实验步骤5. 实验数据记录5.4 基于MATLAB控制系统的博德图及其频域分析1. 实验目的2. 实验原理3. 实验内容4. 实验步骤5. 实验数据记录2.2典型环节模拟电路及其数学模型1.实验目的1)掌握典型环节模拟电路的构成,学习运用模拟电子组件构造控制系统。
2)观察和安装个典型环节的单位节阶跃响应曲线,掌握它们各自特性。
3)掌握各典型环节的特性参数的测量方法,并根据阶跃响应曲线建立传递函数。
2.实验原理本实验通过实验测试法建立控制系统的实验模型。
实验测试法是人为地给系统施加某种测试信号,记录基本输出响应,并用适当的数学模型区逼近。
常用的实验测试法有三种:时域测试法,频域测试法和统计相关测试法。
通过控制系统的时域测试,可以测量系统的静态特性和动态特性指标。
静态特性是指系统稳态是的输入与输出的关系,用静态特性参数来表征,如增益和稳态误差。
动态性能指标是表征系统输入一定控制信号,输出量随时间变化的响应,常用的动态性能指标有超调量、调节时间、上升时间、峰值时间和振荡次数等。
静态特性可以采用逐点测量法,及给新一个输入量,新颖测量被控对象的一个稳态输出量,利用一组数据绘出静态特性曲线求出其斜率,就可以确定被测对象的增益。
动态特性可以采用阶跃响应或脉冲响应测试法,给定被测对象施加阶跃输入信号或脉冲信号,利用示波器或记录仪测量被测对象的输出响应,如为使测量尽可能的得到理想的数学模型,应注意以下几点:1)被测对象应处于实际经常使用的负荷情况,并且在较为稳定的状态下进行测试。
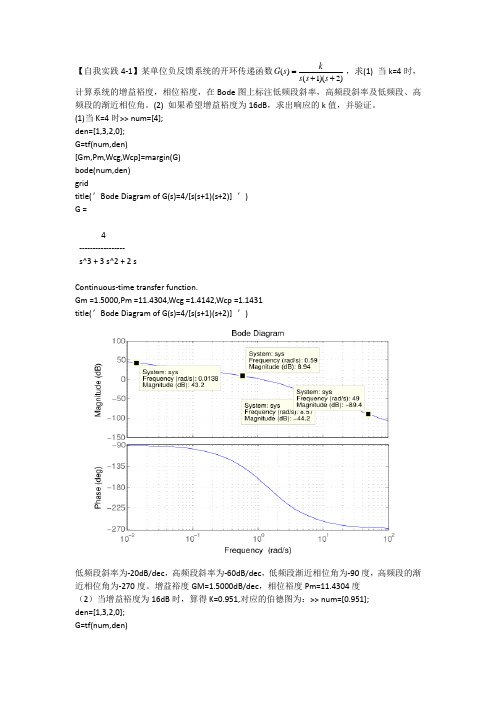
【自我实践4-1】某单位负反馈系统的开环传递函数()(1)(2)kG s s s s =++,求(1) 当k=4时,计算系统的增益裕度,相位裕度,在Bode 图上标注低频段斜率,高频段斜率及低频段、高频段的渐近相位角。
(2) 如果希望增益裕度为16dB ,求出响应的k 值,并验证。
(1)当K=4时>> num=[4]; den=[1,3,2,0]; G=tf(num,den)[Gm,Pm,Wcg,Wcp]=margin(G) bode(num,den) gridtitle(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′) G =4----------------- s^3 + 3 s^2 + 2 sContinuous -time transfer function.Gm =1.5000,Pm =11.4304,Wcg =1.4142,Wcp =1.1431 title(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′)低频段斜率为-20dB/dec ,高频段斜率为-60dB/dec ,低频段渐近相位角为-90度,高频段的渐近相位角为-270度。
增益裕度GM=1.5000dB/dec ,相位裕度Pm=11.4304度 (2)当增益裕度为16dB 时,算得K=0.951,对应的伯德图为:>> num=[0.951]; den=[1,3,2,0]; G=tf(num,den)[Gm,Pm,Wcg,Wcp]=margin(G) bode(num,den) gridtitle(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′) G = 0.951 ----------------- s^3 + 3 s^2 + 2 sContinuous -time transfer function.Gm =6.3091,Pm =54.7839,Wcg =1.4142,Wcp =0.4276 title(′Bode Diagram ′)【自我实践4-2】系统开环传递函数()(0.51)(0.11)kG s s s s =++,试分析系统的稳定性。

最新自控实验报告实验三实验目的:1. 理解并掌握自控系统的基本原理和工作机制。
2. 学习如何搭建和调试简单的闭环控制系统。
3. 通过实验数据分析,加深对系统稳定性和响应特性的认识。
实验设备:1. 自动控制系统实验台。
2. 直流电机及调速器。
3. 传感器(如光电编码器)。
4. 数据采集卡及计算机。
5. 相关软件(如LabVIEW、MATLAB等)。
实验步骤:1. 按照实验指导书的要求,搭建闭环控制系统,包括电机、传感器和控制器。
2. 使用数据采集卡连接传感器和计算机,确保数据传输无误。
3. 开启实验软件,设置相应的参数,如控制算法(PID)、采样时间等。
4. 进行系统开环测试,记录电机的响应数据。
5. 切换至闭环模式,调整PID参数,进行系统调试,直至达到预期的控制效果。
6. 收集闭环控制下的数据,并进行分析,绘制系统响应曲线。
7. 分析系统的稳定性、过渡过程和稳态误差等性能指标。
实验结果:1. 系统开环测试结果显示,电机响应存在较大的超调和振荡。
2. 闭环控制调试后,系统响应速度加快,超调量减小,振荡减少。
3. 通过调整PID参数,系统达到较快的响应时间和较小的稳态误差。
4. 实验数据表明,所设计的控制系统能有效改善电机的动态和稳态性能。
结论:通过本次实验,我们成功搭建并调试了一个简单的闭环控制系统。
实验结果表明,合理的PID参数设置对于提高系统性能至关重要。
此外,实验过程中我们也加深了对自动控制系统原理的理解,为后续更复杂系统的设计和分析打下了坚实的基础。

第1篇一、实验目的1. 理解自控制原理的基本概念和基本方法。
2. 掌握典型控制系统的组成和基本工作原理。
3. 学习使用实验仪器,进行控制系统模拟实验。
4. 分析和评估控制系统的性能指标,提高对控制系统设计和优化的认识。
二、实验仪器与设备1. EL-AT-III型自动控制系统实验箱一台2. 计算机一台3. 万用表一个三、实验原理1. 自控制原理基本概念:自控制原理是研究如何利用反馈信息来控制系统的行为,使其达到预定的目标。
其基本原理是:通过将系统的输出信号反馈到输入端,与输入信号进行比较,产生误差信号,然后根据误差信号调整系统的控制策略,以达到控制目标。
2. 典型控制系统组成:典型控制系统通常由控制器、被控对象、反馈环节和执行机构组成。
3. 控制系统模拟实验:利用实验箱和计算机,通过模拟电路搭建典型控制系统,进行实验研究。
四、实验内容1. 实验一:典型环节及其阶跃响应- 实验目的:掌握控制模拟实验的基本原理和一般方法,掌握控制系统时域性能指标的测量方法。
- 实验步骤:1. 搭建一阶系统的模拟电路。
2. 通过计算机等测量仪器,测量系统的输出,得到系统的动态响应曲线及性能指标。
3. 改变系统的参数,分析参数对系统性能的影响。
2. 实验二:二阶系统阶跃响应- 实验目的:了解二阶系统的阶跃响应特性,掌握二阶系统的性能指标。
- 实验步骤:1. 搭建二阶系统的模拟电路。
2. 通过计算机等测量仪器,测量系统的输出,得到系统的阶跃响应曲线及性能指标。
3. 分析二阶系统的性能指标,如上升时间、超调量、调节时间等。
3. 实验三:连续系统串联校正- 实验目的:学习连续系统串联校正方法,提高控制系统的性能。
- 实验步骤:1. 搭建连续系统的模拟电路。
2. 分析系统的性能指标,确定校正方法。
3. 通过计算机等测量仪器,测量校正后的系统输出,评估校正效果。
五、实验结果与分析1. 实验一:通过搭建一阶系统的模拟电路,测量系统的输出,得到系统的动态响应曲线及性能指标。

自控原理实验报告自控原理实验报告引言:自控原理是现代控制工程的基础理论之一,它研究的是如何通过控制器对系统进行调节,使得系统能够在给定的条件下稳定运行。
本实验旨在通过实际操作,验证自控原理的有效性,并探究其在工程领域的应用。
一、实验目的本实验的主要目的是通过搭建一个简单的自控系统,观察和分析系统的动态响应,并根据实验结果验证自控原理的有效性。
同时,通过实际操作,掌握自控系统的调节方法和技巧。
二、实验装置和原理本实验所使用的装置主要包括一个控制器、一个传感器和一个执行器。
控制器负责接收传感器采集到的数据,并根据预设的控制算法计算出控制信号,然后将控制信号发送给执行器,从而调节系统的输出。
传感器用于采集系统的实时数据,执行器则根据控制信号调节系统的输出。
三、实验步骤1. 首先,将传感器与控制器连接,并将控制器与执行器连接。
2. 打开控制器,设置控制算法和控制参数。
3. 对系统进行初始状态调整,使其达到稳定状态。
4. 改变系统的输入,观察系统的动态响应。
5. 根据观察到的动态响应,调整控制参数,使系统的输出达到预期要求。
6. 重复步骤4和步骤5,直到系统的输出稳定在预期范围内。
四、实验结果与分析在实验过程中,我们观察到系统的输出随着输入的改变而发生变化。
通过调整控制参数,我们成功地将系统的输出稳定在预期范围内。
这表明自控原理在控制系统中具有重要的应用价值。
五、实验总结通过本次实验,我们深入了解了自控原理的基本概念和应用方法。
通过实际操作,我们掌握了自控系统的调节技巧,并验证了自控原理的有效性。
自控原理在工程领域具有广泛的应用,可以用于控制各种系统的稳定性和性能。
在今后的学习和工作中,我们将继续深入研究自控原理,并将其应用于实际工程中。
六、参考文献[1] 李晓明. 自控原理及其应用[M]. 电子工业出版社, 2010.[2] 王志勇. 自控原理与控制工程实践[M]. 机械工业出版社, 2015.结语:通过本次实验,我们对自控原理有了更深入的了解,并学会了如何应用自控原理进行系统控制。
2016〜2017学年第一学期〈〈自动控制原理》实验报告年级:2014级班号:姓名:He学号:成绩:教师:实验设备及编号:实验同组人名单:实验地点:电气工程学院自动控制原理实验室实验时间:2016年10月目录:实验一典型环节的电路模拟 (3)一、实验目的................................................................. 3..二、实验内容................................................................. 3..三、实验电路图及参数.......................................................... 3.四、实验分析 ................................................................ 1.0五、实验思考题............................................................... 1.1实验二二阶系统的瞬态响应. (12)一、实验目的................................................................. 1.2二、实验设备................................................................. 1.2三、实验电路图及其传递函数................................................... 1.2四、实验结果及相应参数 (14)五、实验分析................................................................. 1.6六、实验思考题............................................................... 1.6实验五典型环节和系统频率特性的测量 (17)一、实验目的................................................................. 1.7二、实验设备................................................................. 1.7三、传递函数•模拟电路图及波特图 ............................................. 1.7四、实验思考题 (22)实验六线性定常系统的申联校正 (24)一、实验目的 (24)二、实验设备 (24)三、实验电路图及其实验结果 (24)四、实验分析 (28)五、实验思考题 (28)实验七单闭环直流调速系统 (29)一、实验目的 (29)二、实验设备 (29)三、P ID参数记录表及其对应图像.............................................. .3.0四、P ID控制参数对直流电机运行的影响 (37)实验一典型环节的电路模拟一、 实验目的1. 熟悉THKKL-B 型模块化自控原理实验系统及“自控原理软件”的使用;2. 熟悉各典型环节的阶跃响应特性及其电路模拟;3. 测量各典型环节的阶跃响应曲线,并了解参数变化对其动态特性的影响。
第一章 硬件资源EL-AT-III 型实验系统主要由计算机、AD/DA 采集卡、自动控制原理实验箱、打印机(可选)组成如图1,其中计算机根据不同的实验分别起信号产生、测量、显示、系统控制和数据处理的作用,打印机主要记录各种实验数据和结果,实验箱主要构造被控模拟对象。
图1 实验系统构成实验箱面板如图2:图2 实验箱面板下面主要介绍实验箱的构成:一、 系统电源EL-AT-III 系统采用本公司生产的高性能开关电源作为系统的工作电源,其主要技术性能指标为:1. 输入电压:AC 220V2. 输出电压/电流:+12V/0.5A,-12V/0.5A,+5V/2A3. 输出功率:22W4. 工作环境:-5℃~+40℃。
二、 AD/DA 采集卡AD/DA 采集卡如图3采用CYGNAL 的C8051F410/2芯片做为主控芯片,负责数据采集和USB 通信,AD 采样位数为10位,采样率为1KHz 。
DA 转换位数为10位,转换速率为1K 。
AD/DA 采集卡有两路输出(DA1、DA2)和两路输入(AD1、AD2),其输入和输出电压均为-5V ~+5V 。
显示器 计算机 打印机 实验箱电路 AD/DA 卡图3 AD/DA采集卡三、实验箱面板AD/DA卡输入输出模块实验模块1 实验模块2电源模块模拟开关二极管区EL-CAT-II实验模块3 电阻、电容、二极管区实验模块4 变阻箱、变容箱模块实验模块5 实验模块8实验模块6 实验模块7图4 实验箱面板布局实验箱面板主要由以下几部分构成:1.实验模块本实验系统有八组由放大器、电阻、电容组成的实验模块。
每个模块中都有一个由UA741构成的放大器和若干个电阻、电容。
这样通过对这八个实验模块的灵活组合便可构造出各种型式和阶次的模拟环节和控制系统。
2.二极管,电阻、电容、二极管区这些区域主要提供实验所需的二极管、电阻和电容。
3.AD/DA卡输入输出模块该区域是引出AD/DA卡的输入输出端,一共引出两路输出端和两路输入端,分别是DA1、DA2,AD1、AD2。
自控原理实验指导书实验名称:自控原理实验指导书前言:自控原理是现代自动控制领域的一门重要课程,它研究各种自动控制系统和控制原理的基本原理和方法。
为了帮助同学们更好地理解和掌握自控原理的实验内容和操作过程,本实验指导书将详细介绍实验的目的、原理、实验装置、实验步骤及数据处理等内容。
请同学们仔细阅读并按照指导书的要求完成实验。
实验目的:本实验旨在通过搭建自控原理实验装置,学习并掌握比例控制、积分控制和微分控制等基本控制方法,进一步加深对自控原理的理解。
实验原理:自控原理实验涉及的基本原理主要包括反馈原理、比例控制、积分控制和微分控制。
1. 反馈原理反馈原理是自控系统中最基本的原理之一。
根据反馈原理,系统的控制量与被控制量之间存在一种反馈关系,控制量根据被控制量的变化情况进行调整,以实现对被控制量的稳定控制。
2. 比例控制比例控制是根据被控制量与给定值之间的差异进行控制。
控制量与被控制量的偏差乘以比例系数得到控制量的输出,将输出信号作用于执行元件,从而实现对被控制量的控制。
3. 积分控制积分控制是根据被控制量与给定值之间的累积误差进行控制。
在一定时间内,系统之中的误差累积,并根据累积误差与积分系数的乘积得到控制量的输出,通过执行元件对被控制量进行控制。
4. 微分控制微分控制是根据被控制量的变化趋势进行控制。
通过对被控制量的变化速率进行测量,乘以微分系数得到控制量的输出,通过执行元件对被控制量进行控制,以实现对被控制量的控制。
实验装置:实验装置主要包括自控原理实验箱、电源、信号发生器、数字多用表等。
实验步骤:以下是本实验的具体操作步骤,请同学们按照步骤一步步进行。
1. 连接实验装置:将电源、信号发生器和数字多用表分别接入实验箱的相应接口。
2. 设定实验参数:根据实验要求,设置信号发生器的频率、幅值等参数,并将其输出接入实验箱。
3. 搭建反馈回路:根据实验要求,搭建反馈回路,包括反馈元件、控制器、执行元件等。
实验三 线性系统的频域分析
一、实验目的
1.掌握用MATLAB 语句绘制各种频域曲线。
2.掌握控制系统的频域分析方法。
二、基础知识及MATLAB 函数
频域分析法是应用频域特性研究控制系统的一种经典方法。
它是通过研究系统对正弦信号下的稳态和动态响应特性来分析系统的。
采用这种方法可直观的表达出系统的频率特性,分析方法比较简单,物理概念明确。
1.频率曲线主要包括三种:Nyquist 图、Bode 图和Nichols 图。
1)Nyquist 图的绘制与分析
MATLAB 中绘制系统Nyquist 图的函数调用格式为:
nyquist(num,den) 频率响应w 的范围由软件自动设定
nyquist(num,den,w) 频率响应w 的范围由人工设定
[Re,Im]= nyquist(num,den) 返回奈氏曲线的实部和虚部向量,不作图
例4-1:已知系统的开环传递函数为25262)(23++++=
s s s s s G ,试绘制Nyquist 图,并判断系统的稳定性。
num=[2 6];
den=[1 2 5 2];
nyquist(num,den)
极点的显示结果及绘制的Nyquist 图如图4-1所示。
由于系统的开环右根数P=0,系统的Nyquist 曲线没有逆时针包围(-1,j0)点,所以闭环系统稳定。
p =
-0.7666 + 1.9227i
-0.7666 - 1.9227i
-0.4668
图4-1 开环极点的显示结果及Nyquist 图
若上例要求绘制)10,10(32-∈ω间的Nyquist 图,则对应的MATLAB 语句为:
num=[2 6];
den=[1 2 5 2];
w=logspace(-1,1,100); 即在10-1和101
之间,产生100个等距离的点 nyquist(num,den,w)
2)Bode 图的绘制与分析
系统的Bode 图又称为系统频率特性的对数坐标图。
Bode 图有两张图,分别绘制开环频率特性的幅值和相位与角频率ω的关系曲线,称为对数幅频特性曲线和对数相频特性曲线。
MATLAB 中绘制系统Bode 图的函数调用格式为:
bode(num,den) 频率响应w 的范围由软件自动设定
bode(num,den,w) 频率响应w 的范围由人工设定
[mag,phase,w]=bode(num,den,w) 指定幅值范围和相角范围的伯德图
例4-2:已知开环传递函数为)10016()
12.0(30)(2+++=s s s s s G ,试绘制系统的伯德图。
num=[0 0 15 30];
den=[1 16 100 0];
w=logspace(-2,3,100);
bode(num,den,w)
grid
绘制的Bode 图如图4-2(a)所示,其频率范围由人工选定,而伯德图的幅值范围和相角范围是自动确定的。
当需要指定幅值范围和相角范围时,则需用下面的功能指令:
[mag,phase,w]=bode(num,den,w)
mag,phase 是指系统频率响应的幅值和相角,由所选频率点的w 值计算得出。
其中,幅值的单位为dB,它的算式为magdB=20lg10(mag)。
指定幅值范围和相角范围的MATLAB调用语句如下,图形如图4-2(b)所示。
num=[0 0 15 30];
den=[1 16 100 0];
w=logspace(-2,3,100);
[mag,phase,w]=bode(num,den,w); %指定Bode图的幅值范围和相角范围
subplot(2,1,1); %将图形窗口分为2*1个子图,在第1个子图处绘制图形semilogx(w,20*log10(mag)); %使用半对数刻度绘图,X轴为log10刻度,Y轴为线性刻度
grid on
xlabel(‘w/s^-1’); ylabel(‘L(w)/dB’);
title(‘Bode Diagram of G(s)=30(1+0.2s)/[s(s^2+16s+100)]’);
subplot(2,1,2);%将图形窗口分为2*1个子图,在第2个子图处绘制图形
semilogx(w,phase);
grid on
xlabel(‘w/s^-1’); ylabel(‘ (0)’);
注意:半Bode图的绘制可用semilgx函数实现,其调用格式为semilogx(w,L),其中L=20*log10(abs(mag))。
2.幅值裕量和相位裕量
幅值裕量和相位裕量是衡量控制系统相对稳定性的重要指标,需要经过复杂的运算求取。
应用MATLAB功能指令可以方便地求解幅值裕量和相位裕量。
其MATLAB调用格式为:
[Gm,Pm,Wcg,Wcp]=margin(num,den)
其中,Gm,Pm分别为系统的幅值裕量和相位裕量,而Wcg,Wcp分别为幅值裕量和相位裕量处相应的频率值。
另外,还可以先作bode图,再在图上标注幅值裕量Gm和对应的频率Wcg,相位裕量Pm和对应的频率Wcp。
其函数调用格式为:
margin(num,den)
例4-4:对于例4-3中的系统,求其稳定裕度,对应的MA TLAB语句如下:
num=10; den=[1 3 9 0];
[gm,pm,wcg,wcp]=margin(num,den);
gm,pm,wcg,wcp
gm = 2.7000
pm = 64.6998
wcg = 3.0000
wcp = 1.1936
如果已知系统的频域响应数据,还可以由下面的格式调用函数:
[Gm,Pm,Wcg,Wcp]=margin(mag,phase,w)
其中(mag,phase,w )分别为频域响应的幅值、相位与频率向量。
三、实验内容
1.典型二阶系统
2222)(n n n
s s s G ωζωω++=
绘制出6=n ω,1.0=ζ,0.3,0.5,0.8,2的bode 图,记录并分析ζ对系统bode 图的影响。
程序:
num=[0 0 36];den1=[1 1.2 36];den2=[1 3.6 36];
den3=[1 6 36];den4=[1 9.6 36];den5=[1 24 36];
w=logspace(-2,3,100);
bode(num,den1,w);hold
bode(num,den2,w);
bode(num,den3,w);
bode(num,den4,w);
bode(num,den5,w);
grid
运行结果
结果分析:
2.系统的开环传递函数为
)
5)(15(10
)(2+-=s s s s G )106)(15()
1(8)(22++++=s s s s s s G
)11.0)(105.0)(102.0()
13/(4)(++++=s s s s s s G
绘制系统的Nyquist 曲线、Bode 图,说明系统的稳定性。
Nyquist 曲线:
Bode图:
四、实验报告
1.根据内容要求,写出调试好的MATLAB语言程序,及对应的结果。
2. 记录显示的图形,根据实验结果与各典型环节的频率曲线对比分析。
3. 记录并分析 对二阶系统bode图的影响。
4.根据频域分析方法分析系统,说明频域法分析系统的优点。
5.写出实验的心得与体会。