当前位置：文档之家 › 结构力学 力法ppt课件

结构力学 力法ppt课件

  • 格式：ppt
  • 大小：1.47 MB
  • 文档页数：68

下载文档原格式

  / 68

合集下载

结构力学第6章力法3ppt课件

结构力学第6章力法3ppt课件

X1
1P
11
2 2 FP
-FP
FN
X1 F N1 FNP
2 2
FP
FN1
FNP
FP FNP FP
习惯上列表计算
杆件 l
FN1 FNP
01 a -1/√2 0 13 a -1/√2 -FP 23 a -1/√2 -FP 20 a -1/√2 0 03 √2a +1 √2FP 12 √2a +1 0
• （3）超静定结构内力分布与横梁和桁架 的相对刚度有关。下部链杆截面小，弯 矩图就趋向于简支梁的弯矩图；下部链 杆截面大，弯矩图就趋向于连续梁的弯 矩图。
作业：
• P268 6-5 (a)、6-6
2、超静定组合结构
•计算特点：
•梁式杆：
2
2
ii
F Nil EA
M i dx EI
ik
F Ni F Nkl EA
M i M k dx EI
iP
F Nii FNPl EA
M i M P dx EI
•二力杆：只考虑轴向变形对位移的影响
例:
图示加劲式吊车梁， 1.5m FP=74.2kN
FN12l
1/2×a 1/2×a 1/2×a 1/2×a
√2a √2a
FN1FNPl
FN
0 FP·a /√2 FP·a /√2
0 2FP·a
0
+FP /2 - FP /2 - FP /2 +FP /2 √2FP/2 -√2FP/2
∑
2(1+√2)a (√2+2)
讨论：
• 1、桁架中的杆件(EA=常数)不是去掉
例：用力法计算图示桁架，各杆EA=常数

结构力学力法ppt课件

结构力学力法ppt课件

EI E2I
2 E2I
2 M E 2 M d I x E 1 2 6 I 6 0 1 2 9 3 2 6 0 1 2 9 3 2 E 28 I80
力法
(4) 求多余未知力
18
将系数和自在项代入力法方程，并消去 EI 2 ，得
28X17X2 600 7X132X2 1600
假设X1知，根本体系就是一个静定构造。
怎样 求X1 呢？
力法
二、力法的根本方程
FP
位移条件:根本构造转 化为原构造的条件是：根 本构造在原有荷载和多余
A 原构造
未知力共同作用下，在去
掉多余约束处的位移应与
原构造中相应的位移相等。
A
即
1 0
根本体系
〓
FP 当ΔB=Δ1=0
B
FB
B
X1 =><>=> FB
Δ1P
δ11——根本构造在X1=1单独作用下，B点沿X1方向 的位移。
1 11 10 力法根本方程
Δ11＝δ11X1
δ1X 111P0
δ11和Δ1P都是静定的根本构造在知力作用下的位移，均可用“单位 荷载法〞求得。
力法
用图乘法计算δ11和Δ1P
பைடு நூலகம்δ11
X1=1
Fl
EI
2
↓
B
Δ1P
l
X1=1
M1
MP图
5Fl3 0 48EI
X1
5 16
F
最后的弯矩图可按叠加原理由下式求得： MM1X1M
力法
Fl
EI
2
l
X1=1
M1
MP图
MA
l
5 16

结构力学——力法_图文

结构力学——力法_图文
第五章 力法
学习内容
超静定结构的性质，超静定次数的确定，超静定结构的计算 思想与基本方法；
力法基本概念，荷载作用下用力法计算超静定梁、刚架的内力 对称结构的特性及对称性的利用。 超静定结构的位移计算及力法校核。
学习目的和要求
目的：力法是超静定结构计算的基本方法之一，也是学习 其它方法的基础，非常重要 。
第一节 超静定结构和超静定次数
超静定内力和反力与材料的物理性质、截面的几何特征 （形状和尺寸）有关。
非荷载因素也会使超静定结构内力和反力； 由于有多余约束，所以增强了抵抗破坏的能力； 由于有多余约束，所以增强了超静定结构的整体性，在
荷载作用下会减小位移，内力分布更均匀。
比较静定结构与超静定结构的弯矩图
A1 y01
y02
A
A2
A2
B
ql2/8 MP图
ql2/8
d 11
2 EI
A1 y01
2 EI
(1 1l) ( 2 l)
2
3
2l 3EI
2
2 2 ql 3
l ql 3
Δ1 P
EI
A2 y02
EI
( 3
8
l) ( ) 2 12EI
(5)解方程，求多余未知力X1
X1
Δ1P
d 11
ql 3 3EI 12EI 2l
ql 2
8
()
(6)作内力图
可利用叠加公式
M M1X1 MP
计算和作M图，即
M A 0
0 0
M
D
M M
B E
1 2
1 1 2
ql 2 8
ql 2 0 ql 2
8
8

结构力学讲义ppt课件

结构力学讲义ppt课件
x y
x
结点自由度
y
φ
x
y
x
刚片自由度
2）一个刚片在平面内有三个自由度，因为确定 该刚片在平面内的位置需要三个独立的几何参
数x、y、φ。
4. 约束
凡是能减少体系自由度的装置就称为约束。
6
约束的种类分为：
1）链杆
简单链杆 仅连结两个结点的杆件称为简单 链杆。一根简单链杆能减少一个自由度，故一 根简单链杆相当于一个约束。
FyA
特点： 1) 结构在支座截面可以绕圆柱铰A转动 ； 2) x、y方向的反力通过铰A的中心。
29
3. 辊轴支座
A
A
FyA
特点： 1) 杆端A产生垂直于链杆方向的线位移； 2) 反力沿链杆方向作用，大小未知。
30
4. 滑动支座（定向支座）
A 实际构造
A
MA
FyA
A
MA
FyA
特点： 1）杆端A无转角，不能产生沿链杆方向的线 位移，可以产生垂直于链杆方向的线位移；
16
A
I
II
c)
B III C
形成瞬铰B、C的四根链杆相互平行（不等 长），故铰B、C在同一无穷远点，所以三个 铰A、 B、C位于同一直线上，故体系为瞬变 体系（见图c）。
17
二、举例
解题思路： 基础看作一个大刚片；要区分被约束的刚片及
提供的约束；在被约束对象之间找约束；除复 杂链杆和复杂铰外，约束不能重复使用。
高等教育出版社
4
第一章 绪 论
§1-1 结构力学的内容和学习方法
§1-2 结构计算简图
5
§1-1 结构力学的内容和学习方法
一、结构
建筑物或构筑物中 承受、传递荷载而起 骨架作用的部分称为 结构。如：房屋中的 框架结构、桥梁、大 坝等。

结构力学课件 力法

结构力学课件 力法

（5）叠加原理作M图
M1(m)
M A 360 6 ( 22) 228 M C 6 ( 22) 132
90
228
132
桁架
P
a
（1）基本体系 —基本未知量 （2）位移协调条件 —写力法基本方程 （3）求系数和自由项 —单位荷载法
a
（4）解力法方程 —求基本未知量
P
→ X1 ↑
拆开一个单铰，相当于去掉两个联系。
X1
X 1 ← → ↑ → X2
（3） 在刚结处作一切口，或去掉一个固定端，相当于去掉 三个联系。 X
X1
←→
X2
（4）将刚结改为单铰联结，相当于去掉一个联系。
X1 X1
← →
3
例1: 确定图示结构的超静定次数。
2
1 3
n=6
例2: 确定图示结构的超静定次数。 对于具有较多框格的结构， 可按框格的数目确定，因为一
q a
A
B X1
A
2 力法的基本概念
力法的基本体系
q
A B A
q a
力法的基本未知量
a
B X1
B点的位移条件Δ1=0
变形协调条件
q
A
B A
变形协调条件
Δ1=Δ1P+Δ11=0
Δ1P：基本体系在荷载q单独
a q
A B Δ1P
Δ11 B X1
作用下沿X1方向产生的位移；
Δ11：基本体系在荷载X1单 独作用下沿X1方向产生的 位移；
X1
X1
（1）基本体系 —基本未知量 （2）位移协调条件 —写力法基本方程
a
a
1P 11 X 1 0

结构力学第七章力法.ppt

结构力学第七章力法.ppt
11 ——基本结构在X1=1作用下沿X1方向的位移；
1P ——基本结构在FP作用下沿X1方向的位移。
12
3. 力法计算 1) 求系数及自由项
FPl 2
A
FP
A l/2
MP图
B l
M图
11

1 EI

1 2
l
l

2l 3

l3 3EI
B X1 1
1 p

1 EI

1 2

FPl 2

A θ EI l
B 原结构
A θ EI l
B
基本体系I X1
θ A
EI l
B
X1 基本体系II
（受X1及支座转角θ共同 作用）
（只有X1作用，支座转角θ 对杆端A无影响）
19
解：
1）选两种基本体系如下图示
A θ EI l
B
基本体系I X1
θ A
EI l
B
X1 基本体系II
（受X1及支座转角θ共
同作用）
（只有X1作用，支座转角θ 对杆端A无影响）
2）力法基本方程 位移条件 BV 0 力法方程 11X1 1C 0
A 11X1
20
3）求系数和自由项
A FR1 l
B
A X1=1
B
l
M 图 X1=1
11

1 EI

1 2

l
l

2l 3

l3 3EI
1
M图
11
M M1X1 M2X2 M3X3 M P
FQ FQ1X1 FQ2 X2 FQ3 X3 FQP

《力法结构力学》课件

《力法结构力学》课件
详细描述
力的作用与反作用原理表明，当一个物体对另一个物体施加力时，另一个物体也 会对施力物体施加一个大小相等、方向相反的反作用力。这个原理是牛顿第三定 律的一部分，是理解结构力学中相互作用和平衡状态的基础。
弹性力学的基本假设
总结词
对弹性力学的基本性质和假设的概括。
详细描述
弹性力学的基本假设包括：1) 材料是线弹性的，即应力与应变之间存在线性关系；2) 材料是均匀的，即各部分具有相同的物理性质；3) 材料是无缝的，即不存在内部空隙 或缺陷；4) 材料是连续的，即物质没有离散的间隙或孔洞。这些假设为简化问题和分
来获得结构的响应。
力法结构力学的智能化技术应用
人工智能与机器学习
利用人工智能和机器学习技术对大量 数据进行处理和分析，自动识别结构
的性能特征和优化设计方案。
智能传感器与监测技术
通过智能传感器实时监测结构的性能 状态，实现结构的健康监测和预警。
优化算法与智能决策
将优化算法与人工智能相结合，实现 结构的智能优化设计，提高结构的性
能和可靠性。
感谢您的观看
THANKS03力法结 Nhomakorabea力学的基本方法
静力分析方法
静力分析方法是一种基于平衡条 件的结构分析方法，用于确定结 构在静力荷载作用下的内力和变
形。
静力分析方法主要包括：线弹性 分析、塑性分析和弹塑性分析等
。
静力分析方法广泛应用于各种工 程结构的分析和设计，如桥梁、
房屋、塔架等。
动力分析方法
动力分析方法是一种基于动力 学方程的结构分析方法，用于 确定结构在动力荷载作用下的
总结词
交通工具的力法分析是力法结构力学在交通 运输领域的应用，通过对交通工具进行力法 分析，可以提高交通工具的安全性和舒适性 。

结构力学--力法 ppt课件

结构力学--力法 ppt课件

1 EI
l2
2
2l 3
3lE3I
3 ql 8
X
1
3 8
ql
14
2. 力法求解的基本步骤 ① 选取基本未知量 ② 建立力法基本方程
③ 求解系数δ11和自由项△1P
④ 解方程，求基本未知量 ⑤ 作内力图
15
3. 思考与练习
q
MA
F xA
A
B
F yA
F yB
选择不同的多余约束力作为基本未知量，
力法的基本体系？
第6章 力 法
1
目录
§6-1 超静定结构和超静定次数 §6-2 力法的基本概念 §6-3 力法解超静定刚架和排架 §6-4 力法解超静定桁架和组合结构 §6-5 力法解对称结构 §6-6 力法解两铰拱 §6-7 力法解无铰拱 §6-8 支座移动和温度改变时的力法分析 §6-9 超静定结构位移的计算 §6-10 超静定结构计算的校核 §6-11 用求解器进行力法计算 §6-12 小结
➢土木工程专业的力学可分为两大类，即“结构力学类”和“弹性力学 类”。
“结构力学类”包括理论力学、材料力学和结构力学，其分析方法具有 强烈的工程特征，简化模型是有骨架的体系（质点、杆件或杆系）， 其力法基本未知量一般是“力”，方程形式一般是线性方程。
“弹性力学类”包括弹塑性力学和岩土力学，其思维方式类似于高等数 学体系的建构，由微单元体（高等数学中的微分体）入手分析，简化 模型通常是无骨架的连续介质，其力法基本未知量一般是“应力”， 方程形式通常是微分方程。
➢如果一个问题中既有力的未知量，也有位移的未知量，力的部分考虑 位移约束和变形协调，位移的部分考虑力的平衡，这样一种分析方案 称为混合法。
Strucural Analysis

结构力学力法ppt课件

结构力学力法ppt课件
结构对称一般选取对称基本结构
19
§5-6 超静定结构自内力概念与计算
自内力 — 超静定结构在没有荷载作用情况下，由于
支座移动、温度改变、制造误差等因素产 生的内力。(这是超静定结构所特有的性质)
1. 支座移动
θ
A
EI
已知图示梁A端转动角度
为θ，B端下沉a，求在梁
l
中引起的自内力。
A
B a
B
基本结构
2EI 3 2
4
48EI
2P


M2MP EI
ds

1 (1 1.5EI 2
a
a

1 qa2 ) 2

qa4 6EI
6
④解力法方程：
52

19 48
qa

0

1 3
X1

2 9
X2

1 6
qa

0
得：
X1

7 qa, 16
X2


3 qa 32
⑤画内力图：
M M1X1 M 2X2 M p
24
2111XX112122XX22213 pX3 0 2 p二阶0（对称未(知a)力）
3121XX113222XX22332Xp 303 p 0
33 X3 3 p 0
一阶（反对称未知力）
（线性方程组降阶）
18
说明：
对称超静定结构如果选取对称基本结 构，只要未知力分为对称与反对称，则力 法方程也必然分组，该性质与荷载无关。
4
③求力法方程系数
a a
X1=1 M1图
X2=1
a
M2图

结构力学力法课件

结构力学力法课件

力法典型应用
桁架结构分析：力法在桁架结构分析 中广泛应用，通过计算各杆件的内力， 可以判断结构的安全性和稳定性。
钢框架结构分析：力法可用于钢框架 结构的内力分析和节点设计，确保结 构在地震等荷载作用下的安全性。
梁板结构分析：对于梁板结构，力法 可用于求解弯矩、剪力和轴力等内力 分布，为结构设计提供重要依据。
通过以上内容的学习，可以更好地理 解和掌握结构力学力法的基本原理和 应用，为解决实际工程问题提供有效 的工具。
04
构力学力法
影响线及其应用
01
定义及作用
影响线是用于表示结构在单位移动荷载作用下，某一量值（如内力、位
移等）随荷载位置变化而变化的图形。利用影响线，可以方便地求解结
构在移动荷载作用下的最大响应。
构力学力法件
目录
• 结构力学概述 • 力学基础知识 • 结构力学力法原理 • 结构力学力法进阶技术
01
构力学概述
结构力学定义
• 结构力学定义：结构力学是研究和描述物体在外部载荷作用下 的平衡规律和变形规律的学科。它是固体力学的一个分支，广 泛应用于建筑、航空航天、机械工程等领域。
结构力学的研究对象和内容
02
力学基
静力学基 础
01
02
03
静力学基本概念
介绍静力学的研究对象、 任务和方法，阐述静力学 基本概念，如力、力矩、 平衡等。
静力学公理
阐述静力学公理，如作用 与反作用公理、合力矩定 理、重心定理等，以及其 在解题中的应用。
约束与约束力
介绍约束的概念及分类， 分析各类约束对物体运动 的影响，掌握约束力的求 解方法。
弹性力学基础
弹性力学基本概念
介绍弹性力学的研究对象、基本假设和任务，阐述弹性力学基本概 念，如弹性体、变形、应力、应变等。

结构力学第6章力法2ppt课件38页PPT

结构力学第6章力法2ppt课件38页PPT
= - l3/EI
•⊿1P= -[(1/3×ql2/2×l)×3/4×l
•
+(ql2/2×l )×l )/EI = -5ql4/8EI
•⊿2P=[(ql2/2×l )×l ] =ql4/2EI
（3）、解方程 （求解未知量）
• 力法方程：（可消去 l3/EI）
•
4/3 X 1 -X 2 - 5ql/8 = 0
• (2) 荷载作用下超静定 结构反力、内力的特点：
• 多余力（反力、内力） 的大小只与各杆件的相 对刚度有关，而与其绝 对刚度无关，同一材料 所构成的结构，其反力 内力也与材料的性质 （弹性模量）无关。
• 右上图刚架的各杆弯 矩值与例题中各杆的弯 矩值是否相同？
如不同，为什么？
2、铰接排架
• 计算特点： • 横梁 : EA=∞ • 柱:
• （3）、 X3=1单独作用于基本体系，相应位移
•
δ 13
δ 23
δ 33
• 未知力X3单独作用于基本体系，相应位移
•
δ 13 X3 δ 23 X3 δ 33 X3
• （4）、荷载单独作用于基本体系，相应位移
•
⊿1P
⊿2P
⊿3P
• X1方向的位移⊿1
•
⊿1=δ 11X1+δ 12X2+δ 13X3+ ⊿1P
• 2、系பைடு நூலகம்和自由项
• δ 11 =[(1/2×6×6 )×2/3×6 ]/EI1
•
+[(1/2×6×6)×2/3×6 ]/EI2
• =504/EI2
16/3 23/3
•δ 22=2×[(1/2×3×3)×2/3×3]/EI1
•
+2× [(1/2×3×7 )×(2/3×3+1/3×10)

结构力学第六章力法-PPT课件

结构力学第六章力法-PPT课件

D 1P =
2 δ11 0 0 M M M M M 二、力法的典型方程 i i k i P d = ds 0 , d = ds = 0 , D = ds = ↓↓↓↓↓↓↓↓ ii ik iP δ21 0 B EI EI EI q 0 0 ↓↓↓↓↓↓↓↓
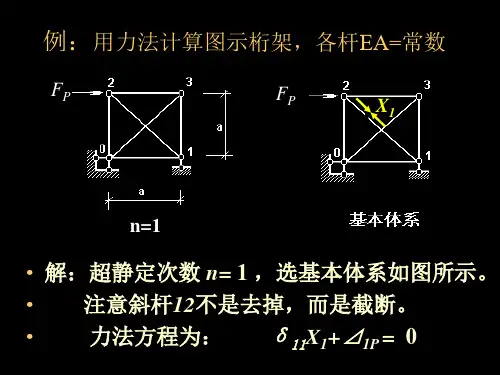
B 主系数恒为正，付系数、自由项可正可负可为零。主系数、付 ΔBH=Δ1 =0 ×X1 系数与外因无关，与基本体系的选取有关，自由项与外因有关。 ＝ ΔBV=Δ2=0 ＝ ＋
6.2 力法的基本概念
一.力法的基本原理
力法的基本概念 1、超静定结构计算的总原则: 欲求超静定结构先取一个基 本体系，然后让基本体系在受 力方面和变形方面与原结构完 全一样。
q ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓B
〓
RB
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓B 当ΔB=Δ1=0
力法的特点： 基本未知量——多余未知力； 基本体系——静定结构； 基本方程——位移条件 （变形协调条件）。
超静定次数 = 多余约束的个数
（ 1）
即: 把原结构变成静定结构时所需撤除的约束个数。
从静力特征来看，超静定次数等于根据平衡方程计算未 知力时所缺少的方程的个数，因此
超静定次数 = 多余未知力的个数 = 未知力个数 - 平衡方程的个数
（ 2）
由 (1) 式确定结构的超静定次数 ，为“解除多余约束 法”。
d
d =l /3 EI 11
l
X1=1 Pl P
Pl
3 D = Pl /2 EI 1 P X 3 P /2 ( ) 1=
M = M X M 1 1 P
MP
1 P l 2
l
M1
M
6.3 超静定结构在荷载作用下的计算

结构力学教学PPT第十章 力法

结构力学教学PPT第十章 力法
P
0 .5 P 0 .5 P
0 .5 P 0 .5 P
MP
MP
5
0 .5 P 0 .5 P
0 .5 P 0 .5 P
MP
d11 X 1 d12 X 2 D1P 0 d 21 X 1 d 22 X 2 D 2 P
0.5P
MP
0
d 33 X 3 D3P 0
X1 X1
I2
I1 I1
X2 X X2 3
4
X1 X1 1
X2 X2 1
X3 1
X3
M1
M2
M3
d11 X 1 d12 X 2 D1P 0 d 21 X 1 d 22 X 2 D 2 P d 33 X 3 D 3P
0 0
d 11 X 1 d 12 X 2 d 13 X 3 D 1P 0 d 21 X 1 d 22 X 2 d 23 X 3 D 2 P 0 d 31 X 1 d 32 X 2 d 33 X 3 D 3P 0
3
§10-1-2 力法基本概念
一、力法基本思路 有多余约束是超静定与静定的根本区别，因此，解决多 余约束中的多余约束力是解超静定的关键。
D1=0 D11=d11x1
D11 + D1P =0 d11x1+ D1P =0
1、力法基本未知量 结构的多余约束中产生的多余未知力（简称多 余力）。 2、力法基本体系 力法基本结构，是原结构拆除多余约束后得到的 静定结构；力法基本体系，是原结构拆除多余约束 后得到的基本结构在荷载（原有各种因素）和多余 力共同作用的体系。 3、力法基本方程 力法基本体系在多余力位置及方向与原结构位移 一致的条件。 方程中的系数和自由项均是静定结构的位移计算 问题，显然，超静定转化为静定问题。

《结构力学力法》课件

《结构力学力法》课件
解题步骤
力法的解题步骤包括构建基本体系、选择基本未知量、建 立线性方程组和求解线性方程组等。
力法的应用范围
静定结构和超静定结构的分析
01
力法可以用于分析静定结构和超静定结构的内力和位移，特别
是对于超静定结构的分析具有重要意义。
复杂结构的分析
02
对于复杂结构，如组合结构、多跨连续结构和空间结构等，力
法同样适用，能够提供有效的解决方案。
边界条件和支座反力的处理
03
力法能够方便地处理结构的边界条件和支座反力，使得问题得
到完整的解决。
力法的解题步骤
构建基本体系
首先需要将原结构拆分成若干个基本体系，以便 于应用力法公式。
建立线性方程组
根据力的平衡和变形协调条件，建立线性方程组 ，并求解该方程组以得到位移和内力。
《结构力学力法》ppt课件
目录
• 引言 • 力法的基本原理 • 力法的实际应用 • 力法的扩展知识 • 总结与展望
01
引言
结构力学的重要性
1
结构力学是土木工程学科中的重要分支，是研究 结构在各种力和力矩作用下的响应和行为的学科 。
2
结构力学对于工程结构的稳定性、安全性和经济 性具有重要意义，是工程设计和施工的基础。
缺点总结
力法需要预先设定结构的初始应力状态，有时难以确定。 力法对于非线性问题的处理能力有限，对于高度非线性结构可能需要
采用其他方法。 力法在处理复杂边界条件和连接时可能存在困难，需要特别注意。
力法在未来的应用前景
随着科技的不断进步和应 用需求的不断提高，力法 在未来的应用前景广阔。
随着新材料和新结构的出 现，力法将面临更多的挑 战和机遇。
力法的计算机实现

《结构力学力法》PPT课件

《结构力学力法》PPT课件

2、刚架：
3、桁架：
第八章 力 法〔Force method〕 §8-1 超静定构造的概念
4、拱：
5、组合构造:
第八章 力 法〔Force method〕
§8-1 超静定构造的概念 三、计算方法
平衡 （ 条 受 件 力 equ ） im l－ ibriu 真实 物 解理 答条 件 力 （ ） 变位
2、超静定构造 ——在任意荷载作用下，其全部内
力、反力不能单用静力平衡条件求出的构造。 (Statically indeterminate (redundant) structure)
几何特点：几何不变，有多余约束。
第八章 力 法〔Force method〕
§8-1 超静定构造的概念 二、种类
1、梁〔连续梁〕：
未知力的位移
“荷载”的位移
消除两者差异 总位移等于已知位移
变形协调条件 力法典型方程
(The Compatibility Equation of Force Method )
多余约束的位置不唯一
第八章 力 法〔Force method〕 §8-2 超静定次数确实定
去掉一个铰相当于去掉两个约束
X1 X2
第八章 力 法〔Force method〕
§8-2 超静定次数确实定
去掉一个固定端相当于去掉两个约束
X3
X1
X2
切断一个梁式杆相当于去掉三个约束
第八章 力 法〔Force method〕
2、解除多余约束，代之以相应的多余未知力。
超静定次数===将原构造转化为静定构造必须
解除的约束〔代之以相应反力〕数。
x2
x1
x1
x2
x2 x1
x1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A
a
B X1
1P 11 X1 0
（3）作出基本结构的 荷载弯矩图，单位弯矩图
（4）求出系数和自由项 —单位荷载法
1P 11 X1 0
0.5qa2
A MP A a M1 1 B B
qa 1P 8EI
X1 1P
4
a3 11 3EI
3 qa 8
11
Ni N Pl EA
§6-3/4 力法解超静定结构
刚架 排架 桁架

组合结构
刚架
20kN/m C I2 A I1 D I2 B
（1）基本体系 —基本未知量 （2）位移协调条件 —写力法基本方程 （3）求系数和自由项 —单位荷载法 （4）解力法方程 —求基本未知量
8m
6m
20kN/m C I2 A 8m I1 D I2 B
a
a
解超静定问题时，我们不是孤立地研究超静定问题， 而是利用静定结构与超静定结构之间的联系，从中找到由
静定问题过渡到超静定问题的途径。
q
A
B
a
q
A B
X1
a
X1 ?
X1
思考
q
A B
B点的位移条件Δ1=0
q
A B Δ 1P Δ11 B X1
a
Δ1P：荷载q单独作用下沿X1方向产生的位移； Δ11：荷载X1单独作用下沿X1方向产生的位移；
A
B
P
C
P 有一个多余联系 有二个多余联系

超静定结构的类型
（1）超静定梁; （2）超静定桁架； （3）超静定拱；
（4）超静定刚架； （5）超静定组合结构。

超静定结构的解法
综合考虑二个方面的条件: （1）平衡条件； （2）几何条件； 具体求解时，有两种基本(经典)方法— 力法和位移法。
力法的基本结构和超静定次数 (1) 基本结构
←↓
X2
（4）将刚结改为单铰联结，相当于去掉一个联系。
X1 X1
← ↓
3
例1: 确定图示结构的超静定次数。
2
1 3
n=6
例2: 确定图示结构的超静定次数。 对于具有较多框格的结构， 可按框格的数目确定，因为一
个封闭框格，其超静定次数等
于 3。 当结构的框格数目为 f ,则 n=3×7=21 n=3f 。
A
0
B
M
小结
1P 11 X1 0
（1）确定基本体系——确定基本未知量 （2）根据位移协调条件——写出力法基本方程 （3）求出系数和自由项——单位荷载法 （4）解力法方程 ——求解基本未知量
P
P X1
B
C
B
C
X2
A
A
11 x1 12 x2 1P 0
21 x1 22 x2 2 P 0
梁、刚架：
ii ij
Mi Ai yi ds EI EI Aj yi Mi M j ds EI EI
2


iP
M i M P ds EI
桁架：
ii ij
Ni l EA
2
Ni N jl EA
iP
§6-2 力法的基本概念P209
Force Method 教学要求：


理解力法的基本概念；
掌握力法的基本解题过程，能够利用力法求解 简单的超静定结构。
§6-2 力法的基本概念P209
Force Method 主要内容： 引例 力法的基本概念 力法解题的基本步骤
1 引例 q
A
q
B
A B
n 次超静定结构力法基本方程：
X X .... X 0 11 1 12 2 1 n n 1 P X X .... X 0 21 1 22 2 2 n n 2 P
.......... X X .... X 0 n 1 1 n 2 2 n n n nP (6 4)
M M X M X .... M X M 1 2 n 1 2 n P
N N X N X .... N X N 1 2 n 1 2 n P
R R X R X .... R X R 1 2 n 1 2 n P
武汉理工大学土木工程与建筑学院
系数和自由项
X1 （1）基本体系 —基本未知量 （2）位移协调条件 —写力法基本方程
6m
1P 11 X1 0
20kN/m C I1 I2 A D
（3）求系数和自由项 —单位荷载法
去掉多余联系后得到的静定结构。
(2) 超静定次数
多余联系或多余未知力的个数。
解除多余联系的方式
去掉或切断一根链杆，相当于去掉一个联系。
↓ X1 ↑
拆开一个单铰，相当于去掉两个联系。
X1
X 1 ← → ↑ ↓ X2
（3） 在刚结处作一切口，或去掉一个固定端，相当于去掉 三个联系。 X
X1
（5）解力法方程 —求解基本未知量
X1为正值，说明基本未知量的方向 与假设方向相同；如为负值，则方 向相反。
q
A B
0.5qa2
A
A a
3 2 qa 8
a
MP
B
B
3 X 1 qa 8
（6）叠加法作弯矩图
M1 MX1
1 2 qa 8
3 X 1 qa 8
1
M M1 X 1 M P
1 2 qa 8
q a
A
B X1
A
2 力法的基本概念
力法的基本体系
q
A B A
q a
力法的基本未知量
a
B X1
B点的位移条件Δ1=0
变形协调条件
q
A
B A
变形协调条件
ΔHale Waihona Puke =Δ1P+Δ11=0Δ1P：基本体系在荷载q单独
a q
A B Δ1P
Δ11 B X1
作用下沿X1方向产生的位移；
Δ11：基本体系在荷载X1单 独作用下沿X1方向产生的 位移；
A
1 1P 11 0
δ11 : 在X1＝1单独作用下，基本 结构沿X1方向产生的位移 根据叠加原理
A
δ11 B X1=1
11 11 X1
1P 11 X1 0
力法的基本方程
3 力法解题的基本步骤 q
A B
a q
（1）确定基本体系 —确定基本未知量
（2）根据位移协调条件 —写出力法基本方程
结构力学课件 力法
第6章
主要内容：
力法
6-1 超静定结构的组成和超静定次数
6-2 力法的基本概念
6-3/4 力法解超静定结构
6-5 对称结构的计算
6-8 支座移动和温度改变时的计算
6-9 超静定结构的位移计算
6-1 超静定结构的组成和超静定次数
超静定结构 几何不变且具有“多余”联系（外部或内部）