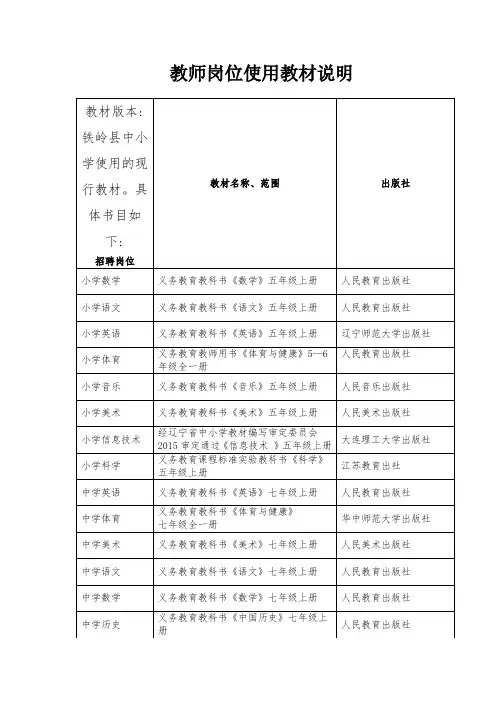
中等职业教育课程改革国家规划新教材

中等职业教育基础课教学改革规划教材：应用文写作中等职业教育基础课教学改革规划教材，是国家为实施中等职业教育的改革而出台的指导教材，其中包括《应用文写作》。

应用文写作作为实施中等职业教育改革的具体实施步骤之一，其目标是帮助学生掌握正确的应用文写作技能，从而提高学生的实际能力。

应用文写作主要有申请信、英语求职信、建议信等几类。

申请信是指申请参加某项活动的信件，通常包括活动的时间、宗旨、服务项目、费用等内容；英语求职信是指申请者向潜在雇主提出求职申请时所写的信件；建议信是指大学生向报考院校申请时所写的信件。

为了帮助学生完成应用文写作，《中等职业教育基础课教学改革规划教材：应用文写作》提出了三大方面的内容：首先是对应用文写作技能进行教学，具体内容包括如何准备书面材料，如何写出文章框架，如何熟练掌握应用文的语言表达技巧，如何制作出符合应用文格式的信件等等；其次是帮助学生建立一个良好的应用文写作思维模式，以帮助他们思考应用文的问题，并将其应用到实践中；第三是将应用文教学中的技能和思维模式应用到实践中，帮助学生完成实际应用文写作任务。

要想行之有效地完成《中等职业教育基础课教学改革规划教材：应用文写作》任务，老师应该采取一系列有效的教学策略。

首先，老师应该及时调整课程内容，以适应技术发展和学生基础；其次，老师要给予学生适当的反馈，让学生能够积极参与课堂活动；第三，老师应该让学生在有意义的情景中进行应用文写作活动，以提高学生的实际写作能力；最后，老师要通过丰富多彩的教学形式，让学生在轻松愉快的氛围中学习应用文写作。

《中等职业教育基础课教学改革规划教材：应用文写作》是指导实施中等职业教育改革的重要教材，它为学生提供了申请信、英语求职信、建议信等内容的学习指导，并针对具体内容提供了技能教学、思维模式建立和实际应用文写作任务的实施指导，也为老师提供了有效的教学策略，以实现教学的有效性。

只有坚持按照《中等职业教育基础课教学改革规划教材：应用文写作》的规定进行教学，才能够帮助学生掌握正确的应用文写作技巧，提高学生的实际能力，实现实施中等职业教育改革的目标。

中等职业教育课程改革国家规划教材《语文》基础
模块(上册)
《语文》基础模块（上册）是中等职业教育课程改革国家规划教材中的一部分。

该教材主要针对中等职业学校的语文课程设置，并根据国家教育改革的要求和中等职
业教育的特点进行编写。

教材内容主要包括语文基础知识、语文基本技能和语文实践
能力的培养。

《语文》基础模块（上册）的教材内容大体可以分为以下几个方面：
1. 语言文字知识：包括语音、字音、词汇、语法、写作等方面的知识，主要培养学生
对语言文字的认识和运用能力。

2. 阅读能力培养：通过选取不同类型的文本，让学生进行阅读理解和分析，培养学生
的阅读能力和语文素养。

3. 写作能力培养：通过教授不同类型的写作形式和写作技巧，指导学生进行写作实践，提高学生的写作能力和表达能力。

4. 口语表达能力培养：通过课堂讨论、演讲、辩论等方式，培养学生的口头表达能力
和交流能力。

5. 文化素养培养：通过学习古代文化、现代文化和外国文化等，提高学生的文化素养
和人文素质。

教材编写注重理论和实践相结合，通过丰富的教学资源和案例分析，激发学生的学习
兴趣和主动性。

教材内容丰富多样，注重培养学生的综合能力和创新思维。

总的来说，《语文》基础模块（上册）是中等职业教育课程改革国家规划教材中的一部分，旨在提高学生的语文素养和综合能力。

教师学科教案[ 20 – 20 学年度第__学期]任教学科：_____________任教年级：_____________任教老师：_____________xx市实验学校3．2函数南市区职教中心宋红燕一、教学目标（一）教学知识点1.常量与变量的概念.2.函数的概念．3.函数的三要素．4.求函数的值．（二）能力训练要求1．使学生理解函数的概念，明确决定函数的三个要素．2．掌握函数值的求法．二、教学重点及难点（一）重点1．函数的概念．2．函数值的求法．（二）难点函数概念的理解．三、教学方法讲授法概念的教学是非常重要的，尤其是学生刚接触一种新的概念，教师给学生讲清楚，并通过师生的共同讨论，帮助学生深刻理解尤为重要．四、教具准备多媒体课件五、教学过程（一）课题导入[师] 观察下列图形，知道：正方形的边长x越长，则它的面积S越_______1.5 2 3[生] 面积S越大．[师]可见，正方形的面积S与它的边长x存在确定的依赖关系，你们能说说看吗？边长x的取值范围是什么？[生] S = x2 ，x R+，其中R+表示正实数集．[师] 现实世界中许多量之间有依赖关系，一个量变化时，另一个量随着起变化．函数是研究各个量之间确定性依赖关系的数学模型．今天，我们就共同来学习函数及其相关概念．（二）讲授新课[师] 当一个量变化时，另一个量随着起变化，我们把某一过程中可以取不同值的量称为变量（variable），始终保持不变的量称为常量（或常数）(constant)．接下来我们给出函数的概念．（板书）如果在某一过程中有两个变量x、y，对于x在某个范围内的每一个确定的值，按照某个对应法则，y都有唯一确定的值与它对应，那么把x叫做自变量(argument)，把y 叫做x的函数(function)，也称y是因变量．我们把自变量x的取值范围记作A，设因变量y从集合B中取值，其中A、B都是实数集的非空子集，简称数集．函数就是数集A到数集B的一个映射．在现代数学文献中，通常把任意一个非空集合到数集的映射都叫做函数．例如：在数字通信中，设A={电位高，电位低}，B={0，1}令f：A B电位低问f是集合A到B的一个映射吗？[生甲] 是[师]回答正确．那么f是集合A上的一个函数吗？[生乙] 是．[师] 非常好．接下来你们能举出一个函数的例子吗？[生丙] 某班学生组成的集合A到这些学生的学号组成的集合B之间的映射是集合A 上的一个函数．[生丁] 补充或改正以上例子．[师]关于函数的概念说明以下三点．1. 函数的概念包含三个要素：定义域、陪域和对应法则．[师]因此两个函数f 与g 相等当且仅当它们的定义域相等，陪域相等，并且对应法则相同．所谓对应法则相同是指定义域中的每一个元素a ，都有f （a ）=g （a ）.2. 函数f ：A B 也可以记成 y =f （x ），x ∈A对于a ∈A ，a 在f 下的像f （a ）称为函数f 在a 处的函数值．所有函数值组成的集合称为函数f 的值域，记作f （A ），即f （A ）= { f （a ）a ∈A }容易看出，f 的值域是f 的陪域的子集，即f （A ） ⊆B.3.到目前为止，同学们认识的数都是实数，因此通常把陪域取成实数集，除非有特别声明．[师]下面开始讲解例题例1 求下列函数在指定处的函数值．（1）f （x ）= 3x –5 在x = –1，x = 2处的函数值．（2）g （x ）= 21x 2 + x –25 在x = –1，x = 3处的函数值． （教师提示，先请学生分析并解答）解: （1）f （-1）= 3×（-1）- 5 = -8, f （2）= 3×2- 5 = 1.（2）g （-1）= 21×2)1(-+（-1）-25 =21 -1 -25 = -3. 求g （3）的过程请学生自己完成．例2 填空：（1）函数y =3x -5把a 对应到b b =_________（2）函数35+=x y 把b 对应到a a =_________ 学生分析并板书解答．完成书上90页试一试（小组完成）（三）课堂练习1.90页A 组1、2、3、4、5（抢答）、6题2.B 组题可以根据时间和学生的学习程度灵活掌握．（四）课时小结由学生自己总结，谈本节学习了哪些内容，教师提示并补充．（派小组代表发言）六、研究性作业1.你能举出一个日常生活中的函数的例子吗？2.请自己设计两道关于求“在指定处的函数值”的题（模仿例1）．七、背景知识与课外阅读如果两个函数的定义域相等，对应法则相同，但是陪域不同，那么这两个函数是不相等的．例如，下述两个函数：f：R R2g：R R+2虽然它们的定义域相等，对应法则相同，但是他们的陪域不同，因此它们不相等．事实上，f不是满射，而g是满射．由此可见f与g的确不相等．。