下载文档原格式
浮点数在计算机中是如何表⽰的话题：浮点数在计算机中是如何表⽰的？回答：浮点数浮点数是属于有理数中某特定⼦集的数的数字表⽰，在计算机中⽤以近似表⽰任意某个实数。
具体的说，这个实数由⼀个整数或定点数（即尾数）乘以某个基数（计算机中通常是2）话题：浮点数的解释回答：浮点数是属于有理数中某特定⼦集的数的数字表⽰，在计算机中⽤以近似表⽰任意某个实数。
具体的说，这个实数由⼀个整数或定点数（即尾数）乘以某个基数（计算机中通常是2）的整数次幂得到，这种表⽰⽅法类似于基数为10的科学记数法。
浮点计算是指浮点数参与的运算，这种运算通常伴随着因为⽆法精确表⽰⽽进⾏的近似或舍⼊。
⼀个浮点数a由两个数m和e来表⽰：a = m * b^e。
在任意⼀个这样的系统中，我们选择⼀个基数b（记数系统的基）和精度p（即使⽤多少位来存储）。
m（即尾数）是形如±d.dddddd的p位数（每⼀位是⼀个介于0到b-1之间的整数，包括0和b-1）。
如果m的第⼀位是⾮0整数，m称作格化的。
有⼀些描述使⽤⼀个单独的符号位（s +或者-）来表⽰正负，这样m必须是正的。
e是指数。
这种设计可以在某个固定长度的存储空间内表⽰定点数⽆法表⽰的更⼤范围的数。
例如，⼀个指数范围为±4的4位⼗进制浮点数可以⽤来表⽰43210,4.321或0.0004321，但是没有⾜够的精度来表⽰432.123和43212.3（必须近似为432.1和43210）。
当然，实际使⽤的位数通常远⼤于4。
此外，浮点数表⽰法通常还包括⼀些特别的数值：+∞和−∞（正负⽆穷⼤）以及NaN('Not a Number')。
⽆穷⼤⽤于数太⼤⽽⽆法表⽰的时候，NaN则指⽰作或者⽆法定义的结果。
众所知，计算机中的所有数据都是以⼆进制表⽰的，浮点数也不例外。
然⽽浮点数的⼆进制表⽰法却不像定点数那么简单了。
先澄清⼀个概念，浮点数并不⼀定等于⼩数，定点数也并不⼀定就是整数。
浮点数的运算方法浮点数是计算机中一种表示实数的数据类型，其特点是可以表示带有小数部分的数字。
在进行浮点数的运算时，需要考虑到浮点数的精度问题、舍入误差以及运算顺序等因素。
浮点数的表示方法为：±m×be，其中m为尾数（即小数部分的数值），b为基数或底数，e为指数（表示位移的量）。
1.浮点数加法运算：-对两个浮点数的指数进行比较，将较小指数的浮点数的尾数左移指数之差的位数，使两个浮点数的小数点对齐。
-对齐后的尾数相加，得到一个和。
-对和进行规格化，即将结果的尾数进行处理，使其满足指定的位数限制。
-对规格化后的结果进行舍入运算，得到最终结果。
2.浮点数减法运算：-先将减数的指数调整与被减数的指数相等。
-对齐后的尾数相减，得到一个差。
-对差进行规格化和舍入运算，得到最终结果。
3.浮点数乘法运算：-将两个浮点数的指数相加，得到加法的和，并相应地调整两个浮点数的尾数。
-尾数相乘，得到一个乘积。
-对乘积进行规格化和舍入运算，得到最终结果。
4.浮点数除法运算：-将被除数的指数减去除数的指数，得到差，并相应地调整两个浮点数的尾数。
-尾数相除，得到一个商。
-对商进行规格化和舍入运算，得到最终结果。
在进行浮点数运算时需要注意一些问题：-浮点数的精度问题：由于浮点数的尾数有限位数，所以会存在精度丢失的问题。
这就意味着进行浮点数运算时，可能会出现舍入误差，导致结果有微小的偏差。
-运算顺序：浮点数的运算顺序可能会影响最终结果。
在连续进行多次浮点数运算时，可能会得到不同的结果。
这是因为浮点数的运算不满足交换律和结合律。
因此，在编程中需要谨慎选择运算顺序，以避免结果的不确定性。
-溢出和下溢问题：由于浮点数的范围限制，可能会出现溢出（结果超出浮点数的表示范围）或下溢（结果过小，无法表示）的情况。
针对这些情况，需要进行特殊处理，如返回特定的错误码或进行科学计数法表示。
在实际编程中，可以使用编程语言提供的浮点数运算库或内置函数来进行浮点数运算，以确保运算结果的准确性和可靠性。
浮点表示方法浮点数是计算机中的一种常见的数值表示法，主要用于表示小数。
在计算机内部，浮点数的表示需要使用特定的方法，这就是浮点表示方法。
下面，就让我们一步步来探究这一方法。
首先，我们需要了解浮点数的结构。
在浮点数中，有两个重要的部分：符号位和数值部分。
符号位决定浮点数的正负，而数值部分则包含了整数位和小数位。
接着，我们需要了解浮点数的精度。
由于计算机内部的存储空间是有限的，所以浮点数的精度是有限的。
在计算机内部，浮点数一般使用32位或64位的二进制数表示。
这意味着浮点数的精度是有限的，可能会存在一些精度误差。
接下来，我们要了解浮点数的表示方法。
在计算机内部，浮点数的表示方法主要有两种：IEEE 754标准和IBM格式。
在这两种方法中，IEEE 754标准是更为常用的一种。
在IEEE 754标准中，一个符号位和数值位都被存储在一个32位或64位的二进制数中。
在这个二进制数中，最高位表示符号，后面的位表示数值。
在数值部分，一定数量的位被用来表示整数部分，剩下的位则被用来表示小数部分。
其中，小数部分的位数称为尾数。
IEEE 754标准又将数值部分分为三个部分：符号位、指数位和尾数位。
指数位的作用是表示浮点数的真实值需要乘以的指数。
最后，我们要了解浮点数常见的错误。
由于浮点数的精度和精确表示有限，计算机进行浮点数运算时会存在一些精度误差。
这就会导致在浮点数计算中出现一些未知的错误。
例如，一些简单的计算可能会得出错误的结果。
以上就是关于浮点表示方法的一些基本内容。
掌握了这些知识，在进行浮点数计算时就可以更加准确地进行。
同时，还需要注意浮点数的精度以及计算中存在的误差，以保证计算结果的准确性。
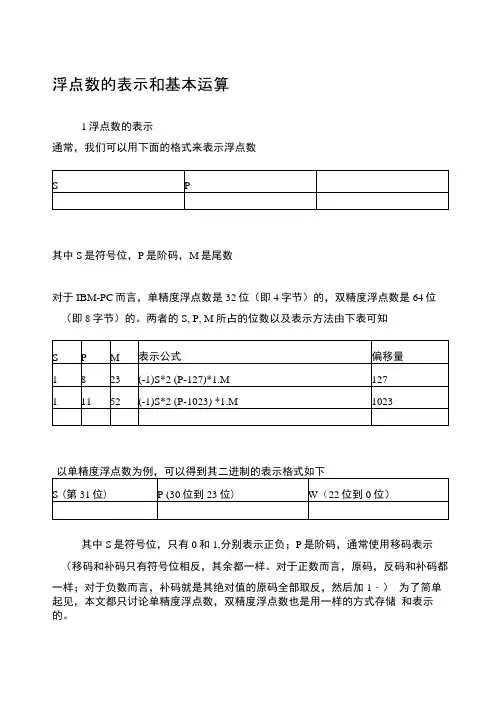
浮点数的表示和基本运算1浮点数的表示通常，我们可以用下面的格式来表示浮点数其中S是符号位，P是阶码，M是尾数对于IBM-PC而言，单精度浮点数是32位（即4字节）的，双精度浮点数是64位（即8字节）的。
两者的S, P, M所占的位数以及表示方法由下表可知以单精度浮点数为例，可以得到其二进制的表示格式如下其中S是符号位，只有0和1,分别表示正负；P是阶码，通常使用移码表示（移码和补码只有符号位相反，其余都一样。
对于正数而言，原码，反码和补码都一样；对于负数而言，补码就是其绝对值的原码全部取反，然后加1・）为了简单起见，本文都只讨论单精度浮点数，双精度浮点数也是用一样的方式存储和表示的。
2浮点数的表示约定单精度浮点数和双精度浮点数都是用IEEE754标准定义的，其中有一些特殊约定。
(1)当P = 0, M 二0 时，表示0。
(2)当P二255, M二0时，表示无穷大，用符号位来确定是正无穷大还是负无穷大。
(3)当F 二255, M !二0 时，表示NaN (Not a Number,不是一个数)。
当我们使用・Net Framework的时候，我们通常会用到下面三个常量Console. WriteLine(float. MaxValue); // 3. 402823E+38Console. WriteLine(float. MinValue); //-3. 402823E+38Console. WriteLine(float. Epsilon); // 1.401298E-45〃如果我们把它们转换成双精度类型，它们的值如下Console. WriteLine(Convert・ ToDouble(float・ MaxValue)); //3.40282346638529E+38Console. WriteLine(Convert・ ToDouble(float・ MinValue)); //-3.40282346638529E+38Console. WriteLine(Convert. ToDouble(float. Epsilon));// 1.401 29846432482E-45那么这些值是如何求出来的呢？根据上面的约定，我们可以知道阶码P的最大值是11111110 (这个值是254,因为2亦用于特殊的约定，那么对于可以精确表示的数来说，254就是最大的阶码T)。
计算机浮点数的表⽰和运算计算机浮点数和存储和运算规则1、概述：众所周知，计算机只能识别⼆进制数据，即所有的⼗进制都需要转换成⼆进制才能在计算机中进⾏存储和运算，但是，⼗进制数有整数部分和⼩数部分，对于整数部分转换成⼆进制数的话，我们采⽤除2取余数法；⼩数部分的话我们采⽤乘2取整法；求出来后，我们对数字进⾏规范化处理；2、来个例⼦：把⼗进制⼩数6.36转换成⼆进制，具体怎么操作？上述例⼦我们把⼀个带⼩数的的⼗进制转换成了⼆进制：但是有没有发现⼀个问题？就是⼩数部分是⼀个⽆限循环的，我们计算机⼀个存储单元可是存不下这么多数据的呀，虽然可以跨存储区，但是⽆限的⼆进制，计算机是存不下的，不可能你定义⼀个数，结果电脑内存或硬盘⽴马塞满导致死机吧？那怎么办呢？进⾏规范化处理3、规范化处理规范化处理是只将⼀个浮点数转换成⼆进制后，根据存储规则，通过符号位+阶码+尾数的形式表⽰该浮点数；data = (-1)^s*M*2*E在Java语⾔中，存储浮点数主要有两种基本数据类型：Float和DoubleFloat：通过Float定义的变量，占4个字节的存储空间，即⼆进制数的长度为32位Double：通过Double定义的变量，占8个字节的存储空间，即⼆进制数的长度位64位注意：计算机表⽰浮点数时，是⽤8位或者11位去存储指数部分，在8位指数位数值上⾯，表⽰0~255，但是我们同样需要有负指数，正负指数的位数量为了均等，各⾃⼀半，-127~128，0是特殊点，特殊处理。
储存时候会加上127，这样就刚刚好是0~255；如果 E 为 11 位，它的取值范围为 0~2047，中间数为1023；这样就能很好的储存了，不然的话，需要判断符号位来判断数值的正负，如下图32位的长度表⽰浮点数时，我们可以得知当E+127>127则代表该数的阶码为正的，如果E+127<127则代表该数的阶码为负的，即01111111为正负数阶码的分隔值。
