当前位置：文档之家 › 高等数学 第七章 第五节 可降阶的高阶微分方程习题课

高等数学 第七章 第五节 可降阶的高阶微分方程习题课

  • 格式：pdf
  • 大小：339.83 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

4.3 可降阶的高阶微分方程

4.3 可降阶的高阶微分方程

2
设原点到A的距离为定值a,初始条件为:
y (0) = a , y '(0) = 0， 令： y ' = p，
dp dx dp 1 2 ⇒ = . = 1+ p ， 方程变为: 2 a dx a 1+ p x 两端积分得：arshp = + C1 , a 由初始条件得 C1 = 0, 故
x dy x x arshp = , p = = sh , y = ach + C 2 . a dx a a
浙江舟山群岛金塘大桥
——连岛工程的第五座跨海大桥 该桥起自金塘岛，接至宁波的镇海炼化厂西侧。按照工 程设计，该桥跨海全长18.5公里，行车道宽度为26米，双 向四车道；设置三个通航孔道，主航道桥采用主跨620米 的双塔双索面斜拉桥方案，通航等级为50000吨级，通航 净空高度51米，通航净宽544米；副航道桥分别采用主跨 为186米的连续刚构和主跨为150米的连续梁桥。金塘大 桥是继东海大桥、杭州湾跨海大桥后国内第三长的跨海 大桥，在舟山大陆连岛工程5座大桥中规模最大。
由初始条件得 C 2 = 0.
于是绳索的状态方程为: (悬链线) x x − x a a y = ach = ( e + e a ). a 2
悬链线的几何意义
x a y = ach = ( e + e a 2
9 8 7 6 5 4 3 2 1 0 -5 -4 -3 -2 -1 0 1 2 3 4 5
代入验证得 C1 = C 2，所以通解为：y = C (e + 1).
x
例5 一离地面很高的物体，受地球引力的作 用由 静止开始落向地面，求它落到地 面的速度和所需的时间。(不计空气阻力) 解:取连接地心与物体的直线为y 轴，其方向为铅直向上, 取地球中心为 原点O，设物体的质量为m，物体开始 下落时距离地心为h，地球半径为R， 质量为Mk为引力系数，时刻t时物体 所在的位置为 y =y(t)，速度为:
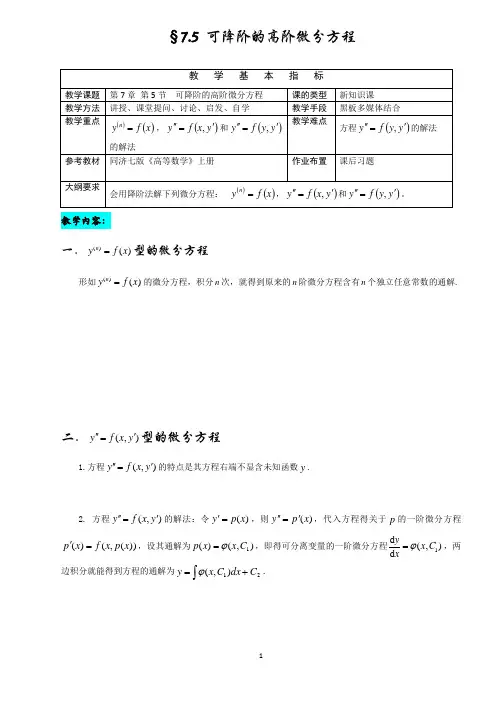
7-5 可降阶的高阶微分方程(高等数学)

7-5 可降阶的高阶微分方程(高等数学)

§7.5 可降阶的高阶微分方程教学内容：一．()()n y f x =型的微分方程 形如()()n y f x =的微分方程，积分n 次，就得到原来的n 阶微分方程含有n 个独立任意常数的通解.二．(,)y f x y '''=型的微分方程1.方程(,)y f x y '''=的特点是其方程右端不显含未知函数y .2. 方程(,)y f x y '''=的解法：令)(x p y ='，则)(x p y '=''，代入方程得关于p 的一阶微分方程))(,()(x p x f x p ='，设其通解为),()(1C x x p ϕ=，即得可分离变量的一阶微分方程1d (,)d =y x C x ϕ，两边积分就能得到方程的通解为⎰+=21),(C dx C x y ϕ.三．(,)y f y y '''=型的微分方程1．方程(,)y f y y '''=的特点是其方程右端不显含自变量x .2. 方程(,)y f y y '''=的解法：令d ()d y p y x=，利用复合函数的求导法则把y ''化为对y 的导数，则d d d d d d d d '''===y p y p y p x y x y,于是方程),(y y f y '=''可化为d (,)d =p p f y p y ,这是关于y 和p 的一阶微分方程，设其通解为),(1C y p ϕ=，即1d (,)d =y y C x ϕ，可求出原方程的通解21d (,)y x C y C ϕ=+⎰.四．例题讲解例1.求微分方程2e x y x '''=+的通解.例2.求微分方程x y x y +'=''1的通解.例3.求微分方程2221e 2()0y y y y y y ''''+-=满足初始条件12e |1x y =-=，12e|e x y =-'=的特解.。

7-5 可降阶的高阶微分方程-精品文档

7-5 可降阶的高阶微分方程-精品文档


解
f( 二、 y x ,y ) 型微分方程
其特点为： 二阶方程中不显含未知 函数 y.
dp 令 p y， 则 y ， 解法： dx
原方程可化为一阶方程
dy ( x ,C ) ， 如果其通解为 p 1 即有 ( x , C ) ， 1 dx 上式两端积分，可得原 方程的通解为 ：
5 3 2 y d x d x d x d x d . 1 2 3 4 5
返回
三、 y f ( y ,y ) 型微分方程
其特点为：二阶方程中不显含自变 量x. dp dp dy dp 则 y p ， 解法：令 p y， dy dx dy dx
2 2 故原方程的通解为 ： C y 1 ( C x C ) . 1 1 2
返回2 例 Fra bibliotek 求方程 y y y 0 的通解 .
d ) (y y 0 , 解 将方程改写成 dx y dy Cdx , 故有 y y C ,即
2 两边积分得通解 y C x C . 1 2
函数 y，一阶线性非齐 解 此二阶方程不显含未知 dp 次微分方程 令 y p， 则y ， dx dp p dp 2 x, x 0 , 即 原方程可化为 x p dx dx x dx dx 从而p y e x xexdx C 1 1 2 1 2 C1 xdx C 1 x x 3 x 13 y x C ln C x . 故原方程的通解为 ： 1 2 9
y ln C cos x 上式两端再积分一次得 2 1 ln 由yx 2 得 C 2 1 2 4 ln cos x . 故所求特解为 ： y
可降阶的高阶微分方程.

可降阶的高阶微分方程.


1 1 将x ' |t 0 0代入 ， C 所以 x ' （ 1 cot 2t） 2m 2m 1 1 再积分 x （t sin 2t） C2 2m 2
将x |t 0 0代入， C2 0
1 1 所求运动规律为x （t程
k 其中k 0为比例系数，记a m
2
d x dx 2 m 2 k ( ) dt dt
2
(1)
x '' a 2 ( x ') 2 x |t 0 0 x ' | 200 t 0
p ' a p
2 2
(2)
令 p x'
(2)变为
(3)
1 2 分离变量 2 dp a dt p
例3 求方程(1x2)y2xy 设yp 则方程yf(x y) 的通解 解 设yp 则原方程化为 化为 pf(x p) (1x2)p2xp 设此方程的通解为 dp 2x 或 p 0 2 pj(xC1) dx 1 x 2x dx 则 yj(xC1) 于是 p C1e1 x 2 C1(1 x2) 于是方程yf(x y)的通解为 即 yC1(1x2) 方程的解法
原方程变为
例4 求方程yyy20的通解
解 设yp 则原方程化为 dp 2 yp p 0 dy dp 1 p 0 ( y0 p0) dy y 1 y dy p C1e C1 y
dp p f ( y, p) dy
或 于是
设此方程的通解为 pj(y C1) dy 即 j ( y, c) dx
p '(1 e ) p 0
x
1 3 y x sin x C1 x C2 6
第五节可降阶的高阶微分方程

第五节可降阶的高阶微分方程

解法：设 y p( y) 则 y dp dy p dP ,
dy dx dy
代入原方程得到新函数P( y)的一阶方程， dy p( y) f ( y, p), dx 先求出P( y),然后求通解y.
例 4 求方程 yy y2 0 的通解.
解1 设 y p( y), 则 y p dP , dy
代入原方程得 y P dP P 2 0, 即 P( y dP P) 0,
dy
dy
由 y dP P 0， dy
可得 P C1 y,
dy dx
C1
y,
原方程通解为 y C2e c1x .
解2 原方程变为 y y , y y
两边积分,得 ln y ln y ln C1， 即 y C1 y，
当y 0,设y p,
y R2 (x C1 )2 C2 . (x C1 )2 ( y C2 )2 R2 .
四、小结
解法 通过代换将其化成较低阶的方程来求解.
补充题: 求方程 xyy xy2 yy 的通解.
解 xyy xy2 yy 同除以y 2得
yy xy2
x(
y2
)
y y
例 6 求曲线，它在任意点处的曲率都等于常数
K( 0). 解 设曲线y y( x),
当y 0,设y p,
则 | y | [1 ( y)2 ]3/2
K,
代入原方程得
dp (1 p2 )3/2
Kdx,
p
1
p2
K(x C1),
p
x C1
,
R2 (x C1)2
R 1 . K
y R2 (x C1)2 C2 .
5. xy y 2 xy .
练习答案
1. y3 y 1 0 .
第五节 可降阶的高阶微分方程

第五节 可降阶的高阶微分方程

dp dp y p = p2 dy
方程化为
dp dy = p y
S2 = ∫ y(t) d t
0
x
解 解 p = C y, 利用定解条件得 C =1,再 y′ = y, 得 得 1 1 x , y = C2 e , 再利用 y (0) = 1 得 C2 =1 故所求曲线方程为
内容小结
可降阶微分方程的解法 —— 降阶法 逐次积分 令 y′ = p(x) , 令 y′ = p(y) ,
B(x, y)
(−1,0) O
(0,1)
vt
x
d x ′2 dx = ∫ 1+ y d t −1
y
代入 ① 式得所求微分方程:
(0,1)
A vt
B(x, y)
(−1,0) O
x
1 x y′′ + 1+ y′2 = 0 即 2 其初始条件为
y
x =−1 = 0,
y′ x=−1 =1
练 习 题
一、求下列各微分方程的通解: 求下列各微分方程的通解: 2、 1、 y ′′′ = xe x ； 2、 y ′′ = 1 + y ′ 2 ； 2 3 y′ 2 = 0 . 4、 3、 y ′′ = ( y ′ ) + y ′ ； 4、 y ′′ + 1− y 求下列各微分方程满足所给初始条件的特解: 二、求下列各微分方程满足所给初始条件的特解: 1、 y 3 y ′′ + 1 = 0 , y x =1 = 1 , y ′x =1 = 0 ； 2、 y ′′ − ay ′ 2 = 0 , y x = 0 = 0 , y ′x = 0 = −1； 3、 y ′′ = 3 y , y x = 0 = 1 , y ′x = 0 = 2 . 三、试 求 y ′′ = x 的 经 过 点 M (0 , 1) 且 在 此 点 与 直 线 x y = + 1相切的积分曲线 . 2
7546;可降阶的高阶微分方程

7546;可降阶的高阶微分方程


分离变量有 dp dy p 0
p 2y
两端积分得
1 ln p 2 ln y ln C1
故 p C1 y
即 再分离变量
dy C1 dx y
ydy C1dx
再积分得 化简得
2
y
3 2
3
C1x C2
3
y 2 C3 x C4
2
或 y (C3 x C4 ) 3
例 7 已知曲线, 它的方程y=f(x)满足微分方程
（降低了阶数，转化 为p与y的关系）
即 y f ( y, y) 不显含x型
解法
：令 y p(x),则
y dp dp dy p dp . dx dy dx dy
代入原方程 p dp f ( y, p) （降低了阶数，转化
dy
为p与y的关系）
设通解为： p ( y, c1),
dy dx
p2
)
ln
y
ln
c1
,
即
1 1 p2
yc1 ,
p 1
Q y 1, y 1, 上式不满足初始条件的解，
x0
x0
考虑 p 1, 即 dy 1, y x c dx
满足初始条件的解为 y=1-x
小 结 1. y(n) f (x)
解法：视 y(n) [ y(n1) ]，积分一次得
（降了一阶）
三、不显含自变量 x 的二阶微分方程
形如 y'' f ( y, y' )的微分方程。
解法： 令y' p,并利用复合函数的求导法则
把y''化为对y的导数，即
y'' dp dp dy p dp y p. dp
dx dy dx dy
高阶微分方程_习题课

高阶微分方程_习题课


故原方程的通解为
1 1 y C1 cos 2 x C 2 sin 2 x x x sin 2 x . 8 8
1 例5 设 y p( x ) y f ( x ) 有一特解为 ，对应 x 的齐次方程有一特解为 x 2，试求： （１） p( x ), f ( x ) 的表达式； （２） 此方程的通解.
高阶方程
特征方程法 幂级数解法 待定系数法
1、可降阶的高阶微分方程的解法
(1) y
( n)
f ( x) 型
解法 接连积分n次，得通解．
( 2)
y f ( x , y ) 型
特点 不显含未知函数y. 解法
令 y P ( x ),
y P ,
代入原方程, 得 P f ( x , P ( x )).
解 （１） 由题设可得：
2 p( x )2 x 0, 解此方程组，得 2 1 p( x )( 2 ) f ( x ), 3 x x
3 f ( x) 3 . x 1 3 （２） 原方程为 y y 3 . x x 显见 y1 1, y2 x 2 是原方程对应的齐次方 程
* 1
1 1 代入 y 4 y x，得 4ax 4b x， 2 2
由
1 4a ， 2
4b 0，
解得
1 y x; 8 b 0，
* 1
1 a ， 8
* (2) 设 y2 x(c cos 2 x d sin 2 x ),
则 ( y ) (c 2dx) cos 2 x (d 2cx ) sin 2 x,
* 2
* ( y2 ) (4d 4cx ) cos 2 x (4c 4dx) sin 2 x,
高等数学课件--D7_5可降阶高阶微分方程

高等数学课件--D7_5可降阶高阶微分方程


x 0
0, 得 C2 1
故所求特解为
2012-10-12
1 e
y
x
目录 上页 下页 返回 结束
同济版高等数学课件
例8.
二阶可导, 且
上任一点 P(x, y) 作该曲线的
切线及 x 轴的垂线, 上述两直线与 x 轴围成的三角形面 积记为 区间[ 0, x ] 上以 为曲边的曲边梯形面积 满足的方程 . 解: 在点 P(x, y) 处的切线倾角为 , 于是
2012-10-12
同济版高等数学课件
目录 上页 下页 返回 结束
例3. 求解 解:
(1 x ) y 2x y
2
y
x0
1,
y
x0
3
代入方程得
(1 x ) p 2x p
2
分离变量
积分得 ln p ln (1 x 2 ) ln C1 ,
利用 y
x0
x
2012-10-12 同济版高等数学课件
目录 上页 下页 返回 结束
内容小结
可降阶微分方程的解法 —— 降阶法
逐次积分 令 y p(x) ,
令 y p( y ) ,
同济版高等数学课件
目录 上页 下页 返回 结束
2012-10-12
思考与练习
1. 方程 如何代换求解 ?
答: 令
或
均可.
目录 上页 下页 返回 结束
dx dt

F0 m
(t
t
2
2T
) C1
利用初始条件
dx dt F0 m (t t
2
得 C1 0, 于是
)
2 3
2T
可降阶的高阶微分方程

可降阶的高阶微分方程

pp f ( y, p)
p( y ) ( y, C1 )
代入 ( 3) 得 :
解此一阶方程, 得 :
即
dy dx ( y , C1 )
dy dx ( y , C1 )
dy ( y, C ) x C2 1
(隐式通解 )
例5
y 2 0 yy

x 例 1 试求 y x 的通过点(0, 1 ) 且在此点与直线 y 2 1
相切的积分曲线.
解
y x 1 y(0) 1, y (0) 2
(4)
(5)
解方程 (4) :
x2 c , y 1 2
y x 3 c1 x c2 (方程通解) . 6
''
代入原方程得:
p 1 pΒιβλιοθήκη 0 x' 1 p( x ) C e
' ' 1

1 dx x
C e
' ln x 1
C x
' 1
y C x
1 ' 2 y C1 x C 2 2
所以 y C1 x 2 C2是原方程的通解.
(1 x 2 ) y 2x y 例4 y x 0 1 , y x 0 3 解 设 y p( x )
解 设 y p( y) , 则 y pp ,
ypp p2 0 代入原方程得: yp p 0 或 p( y) 0
由 即
p 1 p 0 p C1e y
1 y dy
C1e ln y C1 y
C1 x
y C1 y y C 2e
7-5可降阶的高阶微分方程

7-5可降阶的高阶微分方程

第五节 可降阶的高阶微分方程
一、 y(n) f ( x) 型的微分方程 二、 y f ( x, y) 型的微分方程 三、 y f ( y, y) 型的微分方程 四、小结
2019年9月7日星期六
《高等数学》第七章
1
一、 y(n) f ( x) 型的微分方程
特点： 不显含未知函数 y及 y, y,L , y(n1). 解法： 积分 n 次即得通解.
dx
y f ( y, y) 设 y p( y), 则 y p dp
dy
2019年9月7日星期六
《高等数学》第七章
10
例1 求 y x 的通解。
解： y
(x

)dx


x

x

C
y


x

x

C x

C
即为所求通解。
2019年9月7日星期六
《高等数学》第七章
2
例2 求方程 y ex cos x 的通解.
解：
y


ex

sin
x

C
y

乘 不 为 零 因子
y
,
yy y
y

d( dx
y) , y
故 y C y,
从而通解为 y CeCx .
2019年9月7日星期六
《高等数学》第七章
9
四、小结
高阶方程通过代换化成较低阶的方程来求解。 y(n) f ( x) 积分 n 次即得通解. y f ( x, y) 设 y p( x), 则 y dp
解 得 y p C( x ), 由 y x 得 C .

高数-7_5可降阶高阶微分方程-精选文档

x x 两端积分得 Ar y 0 得 C 0 , sh p C ,由 0 1 1 a
设 OA a ,则得定解问题: 1 2 y 1 y a
y
悬链线
M

T
则有
x y sh a
x
两端积分得 y a ch C ,由 yx a , 得 C 0 2 0 2 a x x a x a a 故所求绳索的形状为 y a ch (e e ) a 2
( y ) d y f ( x ) d x 分离变量方程 g
齐次方程
dy y ( ) dx x
dy P(x)y 0 dx
( x ) d x P y C e
一阶线性齐次方程 一阶线性非齐次方程
d y P (x )yQ (x ) d x
P ( x ) d x P ( x ) d x P ( x ) d x y C e Q ( x ) e d x e
目录 上页 下页 返回 结束
H M 点受切向张力T g s ( : 密度, s :弧长) 弧段重力大小
A
g s
x
x yx a , y 0 0 0 H A a dp g s 令 y p ( x ), 则y , 原方程化为 x dx O dp 1 dx 2 2 Ar sh p ln ( p 1 p ) 1 p a
目录 上页 下页 返回 结束
2 x (n ) 一、 y f (x ) 型的微分方程 y e c o sx .
令 z y
(n 1 )
dz ),因此 , 则 y (n) f(x dx
z x ) d x C 1 f(
即
( n 1 ) y f ( x ) d x C 1

4.5可降阶的高阶微分方程 答案详解

4.5 可降阶的高阶微分方程求下列微分方程的通解或特解：1．sin 1y x x '''=++解：()211sin 1d cos 2y x x x x x x C ''=++=-++⎰ 321211sin 62y x x x C x C '=-+++ 432123111cos 2462y x x x C x C x C =+++++ 2．y y x '''=+分析：不显含未知函数y 的二阶微分方程，描述了一阶导与自变量之间的关系，故可作变量代换()y p x '=解：令()y p x '=（注：此处p 为以x 为自变量的新未知函数） 则dp y dx''=，将其代入方程得 dp dp p x p x dx dx=+⇒-=（关于未知函数p 的一阶非齐次线性微分方程） 对应齐次线性方程的通解为(1)12dx x p C e C e --⎰==设非齐次线性方程有形如()x p C x e =的解，将其dp p,dx代入非齐次方程得 ()()()()x x x x C x e C x e C x e x C x xe -''+-=⇒=从而有3()()x x x x x x C x xe dx xde xe e dx xe e C ------==-=--=--+⎰⎰⎰故33()()1x x x x y p x xee C e C e x --'==--+=-- 从而23341()(1)2x x y p x dx C e x dx C e x x C ==--=--+⎰⎰ 3．20yy y '''+=分析：不显含自变量x 的二阶微分方程，描述了一阶导与未知函数本身之间的关系，故可作变量代换()y p y '=解：令()y p y '=（注：此处p 为以y 为自变量的新未知函数）则dp dy dp y p dy dx dy''=⋅=⋅（注：y ''是y '关于x 的导数，故对()p y 关于x 求导，实质上 是复合函数的求导问题，()p y 可视作以y 为中间变量，以x 为自变量的复合函数） 将其代入方程得20dp y p p dy⋅+= 分离变量dp dy p y=-，两边积分1ln ln p y C =-+ 显化()p y 得，1ln ln 322()y y C y p y C e C e y--'==== （注：()p y 计算出来必须显化才能继续计算未知函数y ） 对3C y y'=分离变量得，3ydy C dx = 23412y C x C ⇒=+ 4．20020,0,1x x y y y y ==''''-===-分析：即不显含x 又不显含y ，视作不显含y 情形处理更方便解：令()y p x '=，则dp y dx''=，将其代入方程得 21212022dp dp p dx x C dx p p-=⇒=⇒-=+ 又01x y ='=-，即(0)1p =-，有111011C C -=+⇒=- 从而1()21y p x x '==-+ 21111()(21)ln 21212212y dx d x x C x x ⇒=-=-+=-++++⎰⎰ 又00x y ==，有2210ln 102C C =-+⇒= 故特解为1ln 212y x =-+考研真题：求微分方程2()y x y y ''''+=满足初始条件(1)(1)=1y y '=的特解．解：设()y p x '=，则dp y dx''=，代入方程得2()dp x p p dx += 2d d 1d d p p x x p x x p p p ⎛⎫=⇒+-= ⎪+⎝⎭（注：关于未知函数()p x 的此微分方程不可分离变量，也不是线性的．但倒过来，即将x 视作函数，p 视作自变量后就可视作一阶线性微分方程） 对应齐次线性方程的通解为1()ln 123dp p p x C e C e C p --⎰===设非齐次线性方程有形如()x C p p =的解，将其dx x,dp 代入非齐次方程得 1()()()()1C p p C p C p p p C p p''+-=⇒=，有4()C p p C =+ 从而4()x p C p =+，又(1)1(1)1y p '=⇒=，即441(1)0C C =+⇒=2x p y p '∴=⇒==(1)1p =）从而3252()3y p x dx x C ===+⎰，又51(1)13y C =⇒= 故原方程特解为322133y x =+。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dx dy dx dy 原方程化为： p dp = p3 + p
dy dp = p2 + 1 或 p = 0 dy
dp = p2 + 1
dy
dp p2 + 1 = dy arctan p = y + C1
dy dx
=
p
=
tan( y + )dy
=
dx
ln sin( y + C1 ) = x + ln C2 sin( y + C1 ) = C2e x
= e x[− xe− x − e− x + C1 ] = − x − 1 + C1e x
y = p = − x − 1 + C1e x
y
=
−
1 2
x2
−
x
+ C1e x
+ C2
第七章 第五节
3
2
求解方程
y =
2 xy x2 +1
解
令
p=
y
方程降阶为
p =
2 xp x2 +1
可分离变量微分方程
dp = p
2x x2 + 1 dx
ln p = ln( x2 + 1) + ln C1
y = p = C1( x2 + 1)
y
=
1 C1( 3
x3
+
x) +
C2
第七章 第五节
4
3 求解方程 y3 y = 1
解 令p( y) = y
则
y =
dp = dp dy dx dy dx
=
dp p
dy
原方程化为： y3 p dp = 1 可分离变量 dy
第七章 第五节
2
1 求解方程 y = y + x
y = e − [ P ( x )dx Q( x )e P ( x )dxdx + C ]
解 令 p = y 方程降阶为 p = p + x
一阶非齐次线性方程
分部积分
p = e− (−1)dx[ xe(−1)dxdx + C ] = e x[ xe− xdx + C ]
7.5 可降阶的高阶微分方程习题解答
1 y(n) = f (x) 型，解题思路：连续积分 n 次 2 y" = f (x , y') 型, 特点：不显含因变量 y 解题思路：作因变量换元，令 p = y' 方程降阶为： p' = f (x , p) 3 y" = f (y , y') 型 , 特点：不显含自变量 x
第七章 第五节
6
pdp =
dy y3
p2 = − y−2 + C1
dy = p = C1 y2 − 1
dx
y
ydy = dx
C1 y2 − 1
1 (2
2C1
C1 y2 − 1) = x + C2
第七章 第五节
5
4 求解方程 y = ( y)3 + y
解 令p( y) = y 则 y = dp = dp dy = p dp
解题思路：作自变量换元及因变量换元，令
p( y) = dy
要注意
y =
d
dy ()
=
dp
dy
=
dp p
dx
方程降阶为：
p
dp dy
=
dx dx f ( y ，p)
dy dx
dy
第七章 第五节
1
1 求解方程 y = y + x
2
求解方程
y
=
2 xy x2 +1
3 求解方程 y3 y = 1
4 求解方程 y = ( y)3 + y