第9章压杆稳定

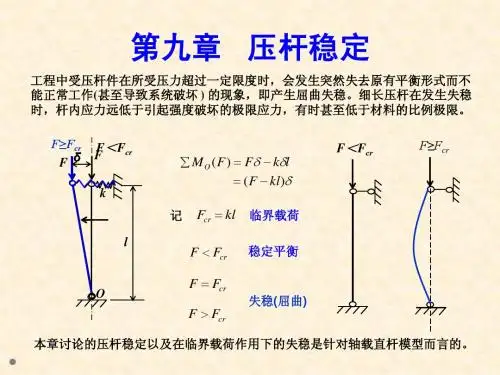
第 九 章 压 杆 稳 定知识要点1 压杆稳定性的概念压杆稳定性是指压杆保持或恢复原有平衡状态的能力。

压杆的临界压力是指压杆由稳定平衡转化为不稳定平衡时所受轴向压力的临界值。

一般由cr F 表示。

2 细长中心受压直杆的临界压力在线弹性和小变形条件下，有着不同杆端约束的细长压杆的欧拉临界压立公式可统一写成()22cr l EI F μπ= 式中，系数μ称为压杆的长度因数，与杆端的约束条件有关。

l μ称为压杆的相当长度，其物理意义是指压杆的挠曲线两个拐点之间的直线距离。

各种常见支撑条件下细长压杆的相当长度和长度系数列于表9-1中。

3 压杆的临界应力总图（1）压杆的柔度（长细比）il μλ= （2）临界应力总图：表示压杆的临界应力随柔度不同而变化的曲线，如土9-1所示。

4 三类压杆的临界力（1） 大柔度杆()P λλ≥临界压力和临界应力按欧拉公式计算()22cr l EI F μπ=22λπσEI cr = il E P p μλσπλ==,2 表9-1各种支撑约束条件下等截面细长压杆临界力的欧公式（2）中柔度杆()P S λλλ≤≤当压杆的临界应力超过比例极限时，压杆的临界应力的计算需按折减弹性模量公式计算22λπσEI cr =式中，r E 为弹性模量，其表达式按压杆截面形式不同而异。

（3）小柔度杆()S λλ≤对于小柔度杆，已不是稳定问题，它属于强度问题，临界应力)(b s cr σσσ或=5 压杆的稳定计算（1）稳定条件 压杆横截面上的工作应力不得超过材料的强度，许用应力与稳定因数ϕ的乘积，即[]σϕσ≤=A F （2）稳定因数ϕ根据试验，有设计规范给出。

①在钢结构设计规范中，钢结构截面分为a,b,c 三类，其稳定因数ϕ被列入文献1的表9-2，9-3中。

②在木结构设计规范中，按树种强度等级给出两种ϕ的计算公式：a 树种强度等级为TC17,TC15 及TB20时2801175⎪⎭⎫ ⎝⎛+=≤λϕλ，23000,75λϕλ=>b 树种强度等级为TC13， TC11 ，TB17及TB15时 2651191⎪⎭⎫ ⎝⎛+=≤λϕλ， 2280091λϕλ=>，习题详解9-1 两端球形铰支的等截面细长压杆，按题9-1图(a)所示坐标系及挠曲线形状，导出的临界力公式为()22cr l EI F μπ= 试分析当分别取题9-1图(a)，(b)，(c)所示坐标系及挠曲线形状时，压杆在cr F 作用下的挠曲线微分方程是否与题9-1图(a)情况下的相同，由此所得的cr F 公式又是否相同。

第九章压杆稳定§9.1 压杆稳定的概念§9.2 两端铰支细长压杆的临界压力§9.3 其它支座条件下细长压杆的临界压力§9.4 欧拉公式的适用范围，经验公式§9.5 压杆的稳定校核§9.6 提高压杆稳定性的措施1. 引言强度——构件抵抗破坏（塑性变形或断裂）之能力2．实例crcr①受均匀外压作用的圆筒形薄壳——由圆形平衡变成椭圆形平衡。

②受均匀压力作用的拱形薄板——由拱形平衡变成翘曲平衡。

③窄高梁或薄腹梁的侧向弯曲——由平面弯曲变成侧向弯曲。

④圆筒形薄壳在轴向压力或扭转作用下引起局部皱折。

⑤细长压杆由直线平衡变成曲线平衡。

3．稳定研究发展简史早在18世纪中叶，欧拉就提出《关于稳定的理论》但是这一理论当时没有受到人们的重视，没有在工程中得到应用。

原因是当时常用的工程材料是铸铁、砖石等脆性材料。

这些材料不易制细细长压杆，金属薄板、薄壳。

随着冶金工业和钢铁工业的发展，压延的细长杆和薄板开始得到应用。

19世纪末20世纪初，欧美各国相继兴建一些大型工程，由于工程师们在设计时，忽略杆件体系或杆件本身的稳定问题向造许多严重的工程事故。

例如：19世纪末，瑞士的《孟希太因》大桥的桁架结构，由于双机车牵引列车超载导致受压弦杆失稳使桥梁破坏，造成200人受难。

弦杆失稳往往使整个工程或结构突然坍蹋，危害严重，由于工程事故不断发生，才使工程师们回想起欧拉在一百多年前所提出的稳定理论。

从此稳定问题才在工程中得到高度重视。

§9.1 压杆稳定的概念 1．工程实例（1当推动摇臂打开气阀时就受压力作用。

（2）磨床液压装置的活塞杆，当驱动工作台移动时受到压力作用。

（3）空气压缩机，蒸汽机的连杆。

（4）桁架结构的某些杆件。

（5）建筑物中的柱。

2．压杆分类⎪⎩⎪⎨⎧⎭⎬⎫--.,,.3.2.1曲线平衡而发生失稳杆件会由直线平衡变成比例极限甚至低于或者强度极限当应力低于屈服极限稳定问题细长杆中长杆强度问题短杆b b s σσσ 3．压杆失稳：压杆由直线形状的稳定平衡而过渡到曲线平衡称为失稳或者屈曲。

第 1 页/共 2 页9-5 未失稳失，轴向压缩 T F L L ∆=∆TEA F TL L EAFL L l l T F αα=⇒=∆=∆， 临界状态 kN 3.109)5.0(22cr ==L EIF π由cr F F =得，温升C EALEI T l ︒==2.29422απ 9-8 由铰B 平衡，22BC AB F F F +=，ABBC F F =θtan F 最大时，AB F 与BC F 均达到临界值2222)sin ()cos (βπβπAC EI F AC EI F BC AB ==， )arctan(cot cot tan 22βθβθ==⇒， 9-10 柔度临界值 p2p σπλE = （1）5.72p =λ，（2）8.65p =λ，（3）6.73p =λ 9-12 AB 与BC 均为两力杆，由铰B 平衡可得 F F BC 75=（压） 柔度 m m 320m 5.215.216=====i l i l，，，其中μμλ 稳定因素 06.028002==λϕ稳定许用应力 MPa 6.0][][st ==σϕσ st ][MPa 58.0σσ<==AF BC ，满意稳定性条件。

9-15 组合压杆的临界力cr F 为杆BC 与AB 临界力的最小值柔度临界值 1002==PP E σπλ P ACAC P BC BC i AC i BC λλλλ>=====1047.0100，大柔度杆，由欧拉公式N 1094.0)7.0(N 1004.1622622⨯==⨯==AC EIF BC EIF AC BC ππ，N 1094.06cr ⨯==⇒AC F F许用压力 kN 376][stcr ==n F F ⎪⎪⎭⎫ ⎝⎛======kN 416MPa 8.82][MPa 1.207BC kN 376MPa 6.76][MPa 4.191AC st cr st cr F F ，，：，，：σσσσ 9-17 杆AC ，强度许用应力 MPa 118][st ==n σσ 最大弯矩 26132bh W F M B ==， 最大应力 kN 6.95][41][2max =≤⇒≤=bh F W M B σσσ 杆CD ，柔度P iCD λλ>==200，大柔度杆 由欧拉公式 MPa 3.4922cr ==λπσE 稳定许用应力 MPa 4.16][st cr st ==n σσ 压力 F F CD 31=应力 kN 5.15][3][st st =≤⇒≤=A F AF CD σσσ 结构的许可荷载 kN 5.15][=F。