标准正态分布曲线N

标准正态分布标准正态分布（英语：standard normal distribution，德语Standardnormalverteilung），是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。

期望值μ=0，即曲线图象对称轴为Y轴，标准差σ=1条件下的正态分布，记为N(0，1)。

定义：标准正态分布又称为u分布，是以0为均数、以1为标准差的正态分布，记为N（0，1）。

标准正态分布曲线下面积分布规律是：在-1.96～+1.96范围内曲线下的面积等于0.9500，在-2.58～+2.58范围内曲线下面积为0.9900。

统计学家还制定了一张统计用表（自由度为∞时），借助该表就可以估计出某些特殊u1和u2值范围内的曲线下面积。

正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线。

我们通常所说的标准正态分布是位置参数均数为0, 尺度参数：标准差为1的正态分布特点：密度函数关于平均值对称平均值与它的众数（statistical mode）以及中位数（median）同一数值。

函数曲线下68.268949%的面积在平均数左右的一个标准差范围内。

95.449974%的面积在平均数左右两个标准差的范围内。

99.730020%的面积在平均数左右三个标准差的范围内。

99.993666%的面积在平均数左右四个标准差的范围内。

函数曲线的反曲点（inflection point）为离平均数一个标准差距离的位置。

标准偏差：深蓝色区域是距平均值小于一个标准差之内的数值范围。

在正态分布中，此范围所占比率为全部数值之68%，根据正态分布，两个标准差之内的比率合起来为95%；三个标准差之内的比率合起来为99%。

在实际应用上，常考虑一组数据具有近似于正态分布的概率分布。

若其假设正确，则约68.3%数值分布在距离平均值有1个标准差之内的范围，约95.4%数值分布在距离平均值有2个标准差之内的范围，以及约99.7%数值分布在距离平均值有3个标准差之内的范围。

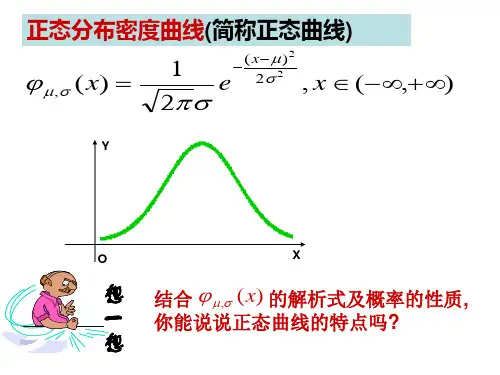
§ 1.5 正态分布山东省德州一中 高级教师 房新宝教学目标：1. 使学生了解正态分布的意义；2. 借助实例研讨，使学生了解正态曲线与正态分布的性质；3. 使学生了解生产过程的质量控制原理； 教学重点：正态分布意义的了解。

教学方法： 实验研讨 教学建议：1. 利用实例研究，引导学生认识正态分布N ()ωσ，2； 2. 利用实例观察标准正记分布N （0，1）；以及分布表； 3. 利用实例引导学生了解生产过程质量测控原理；知识要点巩固与梳理1. 正态分布：总体密度曲线近似地是下面函数的图象；f x e x x ()()()=∈-∞+∞--12222πσμσ，，…………（1） 式中的μσσ，(>0)是参数，分别表示总体的平均数与标准差，这个总体是有限容量的抽象总体，其分布叫做正态分布。

2. 正态曲线正态分布常记作N ()μσ，，（1）的图象被称为正态曲线。

如图1-14，1-15，1-16是三条正态曲线μσ、取值不同。

3. 标准正态总体在函数式（1）中，当μσ==01，时，正态总体称为标准正态总体，此时相应的函数表示式是：f x e x ()()=∈-∞+∞-1222ππ，， (2)4. 标准正态曲线函数式（2）所对应的曲线称为标准正态曲线，它有如下性质： （1）曲线在x 轴上方，与x 轴不相交 （2）曲线关于直线x=0对称 （3）曲线在x=0时位于最高点（4）当x<0时，曲线上升；当x>0时，曲线下降，并且当曲线向左、右两边无限延伸时，此x 轴为渐近线，向它无限靠近。

（5）曲线的形状由σ确定，σ越大，曲线越“矮胖”，表示总体的分布越分散；σ越小，曲线越“瘦高”，表示总体的分布越集中，如图1-17。

由于标准正态曲线关于y 轴对称，表中只给出了对应于非负值x 0的值Φ()x 0，如果x 00<，由图1-18中两个阴影部分面积相等知：ΦΦ()()x x 001=-- 利用“标准正态分布表”可以求出标准正态总体在任一区间（x x 12，）内取值的概率，如图1-19。

标准正态分布怎么算
首先，我们来了解一下标准正态分布的概念。

标准正态分布又称为正态分布或者高斯分布，它是一种连续型的概率分布。

其概率密度函数呈钟形，左右对称，中心峰较高，两侧逐渐减小。

标准正态分布的均值为0，标准差为1，记为N(0,1)。

在标准正态分布曲线下，横坐标为z值，纵坐标为概率密度值。

标准正态分布的曲线下的面积等于1。

其次，我们来了解一下标准正态分布的性质。

标准正态分布具有一些重要的性质，包括对称性、稳定性和独立性。

其中，对称性是指标准正态分布曲线以均值为对称轴对称；稳定性是指标准正态分布的均值和标准差都是固定的；独立性是指标准正态分布的每一个数值都是独立的，不受其他数值的影响。

这些性质使得标准正态分布在实际应用中具有重要的意义。

最后，我们来了解一下标准正态分布的计算方法。

在实际应用中，我们经常需要计算标准正态分布的概率值或者反向求解。

计算标准正态分布的概率值可以通过查表或使用统计软件进行计算。

而反向求解则可以利用标准正态分布的性质和公式进行计算。

在计算过程中，我们需要注意使用标准正态分布的累积分布函数和反函数
来进行计算，以确保计算结果的准确性。

综上所述，标准正态分布在统计学中具有重要的意义，它的概念、性质和计算方法都是我们需要深入了解和掌握的内容。

通过本文的介绍，希望能够帮助读者更加清晰地理解标准正态分布，并能够在实际应用中灵活运用。

正态分布曲线的特点及曲线所表示的意义【知识点的知识】1．正态曲线及性质（1）正态曲线的定义函数φμ，σ（x）＝，x∈（﹣∞，+∞），其中实数μ和σ（σ＞0）为参数，我们称φμ，σ（x）的图象（如图）为正态分布密度曲线，简称正态曲线．（2）正态曲线的解析式①指数的自变量是x定义域是R，即x∈（﹣∞，+∞）．②解析式中含有两个常数：π和e，这是两个无理数．③解析式中含有两个参数：μ和σ，其中μ可取任意实数，σ＞0这是正态分布的两个特征数．④解析式前面有一个系数为，后面是一个以e为底数的指数函数的形式，幂指数为﹣．2．正态分布（1）正态分布的定义及表示如果对于任何实数a，b（a＜b），随机变量X满足P（a＜X≤b）＝φμ，σ（x）dx，则称X的分布为正态分布，记作N（μ，σ2）．（2）正态总体在三个特殊区间内取值的概率值①P（μ﹣σ＜X≤μ+σ）＝0.6826；②P（μ﹣2σ＜X≤μ+2σ）＝0.9544；③P（μ﹣3σ＜X≤μ+3σ）＝0.9974．3．正态曲线的性质正态曲线φμ，σ（x）＝，x∈R有以下性质：（1）曲线位于x轴上方，与x轴不相交；（2）曲线是单峰的，它关于直线x＝μ对称；（3）曲线在x＝μ处达到峰值；（4）曲线与x轴围成的图形的面积为1；（5）当σ一定时，曲线随着μ的变化而沿x轴平移；（6）当μ一定时，曲线的形状由σ确定，σ越小，曲线越“瘦高”，表示总体的分布越集中；σ越大，曲线越“矮胖”，表示总体的分布越分散．4．三个邻域会用正态总体在三个特殊区间内取值的概率值结合正态曲线求随机变量的概率．落在三个邻域之外是小概率事件，这也是对产品进行质量检测的理论依据．【典型例题分析】题型一：概率密度曲线基础考察典例1：设有一正态总体，它的概率密度曲线是函数f（x）的图象，且f（x）＝，则这个正态总体的平均数与标准差分别是（）A．10与8 B．10与2 C．8与10 D．2与10解析：由＝，可知σ＝2，μ＝10．答案：B．典例2：已知随机变量ξ服从正态分布N（2，σ2），且P（ξ＜4）＝0.8，则P（0＜ξ＜2）等于（）A．0.6 B．0.4 C．0.3 D．0.2解析：由P（ξ＜4）＝0.8知P（ξ＞4）＝P（ξ＜0）＝0.2，故P（0＜ξ＜2）＝0.3．故选C．典例3：已知随机变量X服从正态分布N（3，1），且P（2≤X≤4）＝0.682 6，则P（X＞4）等于（）A．0.158 8 B．0.158 7 C．0.158 6 D．0.158 5解析由正态曲线性质知，其图象关于直线x＝3对称，∴P（X＞4）＝0.5﹣P（2≤X≤4）＝0.5﹣×0.682 6＝0.1587．故选B．题型二：正态曲线的性质典例1：若一个正态分布的概率密度函数是一个偶函数，且该函数的最大值为．（1）求该正态分布的概率密度函数的解析式；（2）求正态总体在（﹣4，4]的概率．分析：要确定一个正态分布的概率密度函数的解析式，关键是求解析式中的两个参数μ，σ的值，其中μ决定曲线的对称轴的位置，σ则与曲线的形状和最大值有关．解（1）由于该正态分布的概率密度函数是一个偶函数，所以其图象关于y轴对称，即μ＝0．由＝，得σ＝4，故该正态分布的概率密度函数的解析式是φμ，σ（x）＝，x∈（﹣∞，+∞）．（2）P（﹣4＜X≤4）＝P（0﹣4＜X≤0+4）＝P（μ﹣σ＜X≤μ+σ）＝0.6826．点评：解决此类问题的关键是正确理解函数解析式与正态曲线的关系，掌握函数解析式中参数的取值变化对曲线的影响．典例2：设两个正态分布N（μ1，）（σ1＞0）和N（μ2，）（σ2＞0）的密度函数图象如图所示，则有（）A．μ1＜μ2，σ1＜σ2B．μ1＜μ2，σ1＞σ2C．μ1＞μ2，σ1＜σ2D．μ1＞μ2，σ1＞σ2解析：根据正态分布N（μ，σ2）函数的性质：正态分布曲线是一条关于直线x＝μ对称，在x＝μ处取得最大值的连续钟形曲线；σ越大，曲线的最高点越低且较平缓；反过来，σ越小，曲线的最高点越高且较陡峭，故选A．答案：A．题型三：服从正态分布的概率计算典例1：设X～N（1，22），试求（1）P（﹣1＜X≤3）；（2）P（3＜X≤5）；（3）P（X≥5）．分析：将所求概率转化到（μ﹣σ，μ+σ]．（μ﹣2σ，μ+2σ]或[μ﹣3σ，μ+3σ]上的概率，并利用正态密度曲线的对称性求解．解析：∵X～N（1，22），∴μ＝1，σ＝2．（1）P（﹣1＜X≤3）＝P（1﹣2＜X≤1+2）＝P（μ﹣σ＜X≤μ+σ）＝0.682 6．（2）∵P（3＜X≤5）＝P（﹣3＜X≤﹣1），∴P（3＜X≤5）＝[P（﹣3＜X≤5）﹣P（﹣1＜X≤3）]＝[P（1﹣4＜X≤1+4）﹣P（1﹣2＜X≤1+2）]＝[P（μ﹣2σ＜X≤μ+2σ）﹣P（μ﹣σ＜X≤μ+σ）]＝×（0.954 4﹣0.682 6）＝0.1359．（3）∵P（X≥5）＝P（X≤﹣3），∴P（X≥5）＝[1﹣P（﹣3＜X≤5）]＝[1﹣P（1﹣4＜X≤1+4）]＝[1﹣P（μ﹣2σ＜X≤μ+2σ）]＝×（1﹣0.954 4）＝0.0228．求服从正态分布的随机变量在某个区间取值的概率，只需借助正态曲线的性质，把所求问题转化为已知概率的三个区间上．典例2：随机变量ξ服从正态分布N（1，σ2），已知P（ξ＜0）＝0.3，则P（ξ＜2）＝．解析：由题意可知，正态分布的图象关于直线x＝1对称，所以P（ξ＞2）＝P（ξ＜0）＝0.3，P（ξ＜2）＝1﹣0.3＝0.7．答案：0.7．题型4：正态分布的应用典例1：2011年中国汽车销售量达到1 700万辆，汽车耗油量对汽车的销售有着非常重要的影响，各个汽车制造企业积极采用新技术降低耗油量，某汽车制造公司为调查某种型号的汽车的耗油情况，共抽查了1 200名车主，据统计该种型号的汽车的平均耗油为百公里8.0升，并且汽车的耗油量ξ服从正态分布N（8，σ2），已知耗油量ξ∈[7，9]的概率为0.7，那么耗油量大于9升的汽车大约有辆．解析：由题意可知ξ～N（8，σ2），故正态分布曲线以μ＝8为对称轴，又因为P（7≤ξ≤9）＝0.7，故P（7≤ξ≤9）＝2P（8≤ξ≤9）＝0.7，所以P（8≤ξ≤9）＝0.35，而P（ξ≥8）＝0.5，所以P（ξ＞9）＝0.15，故耗油量大于9升的汽车大约有1 200×0.15＝180辆．点评：服从正态分布的随机变量在一个区间上的概率就是这个区间上，正态密度曲线和x 轴之间的曲边梯形的面积，根据正态密度曲线的对称性，当P（ξ＞x1）＝P（ξ＜x2）时必然有＝μ，这是解决正态分布类试题的一个重要结论．典例2：工厂制造的某机械零件尺寸X服从正态分布N（4，），问在一次正常的试验中，取1 000个零件时，不属于区间（3，5]这个尺寸范围的零件大约有多少个？解∵X～N（4，），∴μ＝4，σ＝．∴不属于区间（3，5]的概率为P（X≤3）+P（X＞5）＝1﹣P（3＜X≤5）＝1﹣P（4﹣1＜X≤4+1）＝1﹣P（μ﹣3σ＜X≤μ+3σ）＝1﹣0.9974＝0.0026≈0.003，∴1 000×0.003＝3（个），即不属于区间（3，5]这个尺寸范围的零件大约有3个．【解题方法点拨】正态分布是高中阶段唯一连续型随机变量的分布，这个考点虽然不是高考的重点，但在近几年新课标高考中多次出现，其中数值计算是考查的一个热点，考生往往不注意对这些数值的记忆而导致解题无从下手或计算错误．对正态分布N（μ，σ2）中两个参数对应的数值及其意义应该理解透彻并记住，且注意第二个数值应该为σ2而不是σ，同时，记住正态密度曲线的六条性质．。

标准正态分布曲线的计算公式为正态分布标准化的公式：Y=（X-μ）/σ～N（0，1）。

证明；因为X～N（μ，σ^2），所以P（x）=（2π）^（-1/2）*σ^（-1）*exp{[-（x-μ）^2]/（2σ^2）}。

注：F（y）为Y的分布函数，Fx（x）为X的分布函数。

而F（y）=P（Y≤y）=P（（X-μ）/σ≤y）=P（X≤σy+μ）=Fx（σy+μ）。

所以p（y）=F'（y）=F'x（σy+μ）*σ=P（σy+μ）*σ=[（2π）^（-1/2）]*e^[-（x^2）/2]。

从而，N（0，1）。

正态分布标准化的意义是可以方便计算，是一种统计学概念。

原本的正态分布图形有高矮胖瘦不同的形态，实际上是积分变换的必然结果，就好比是：
1.y=kx+b直线，它不一定过原点的，但是通过变换就可以了：大Y=y-b；大
X=kx；===>大Y=大X。

2.y=a*b乘积，通过变换就可以变成加法运算：Ln（y）=Lna+Lnb。

3.y=ax²+bx+c通过变换就可以变成标准形式：y=a（x+b/（2a））²+（c-b²
/（4a））。

正态分布的标准化也只不过是“积分变换”而已，虽然高矮胖瘦不同的形态，但是变量的线性伸缩变换并不改变其量化特性，虽然标准化以后都变成期望是0，方差是1的标准分布了，但这种因变量自变量的依赖关系仍然存在，不用担心会“质变”。

正态分布n(μ,σ2)的两个参数正态分布是一种常见的统计分布，它可以用于描述许多自然现象和实验数据。

一个正态分布可以由两个参数来完全描述，分别是均值(μ)和方差(σ^2)。

均值(μ)是正态分布曲线的中心点，它决定了曲线的位置。

在正态分布中，均值是对称的，即曲线左右两侧的面积相等。

均值的选择会直接影响曲线的位置。

当均值增大时，曲线整体向右移动；当均值减小时，曲线整体向左移动。

方差(σ^2)是正态分布曲线的扁平程度，它决定了曲线的形状。

方差越大，曲线越扁平；方差越小，曲线越陡峭。

方差的选择会直接影响曲线的宽度。

当方差增大时，曲线变得更宽；当方差减小时，曲线变得更窄。

正态分布的均值和方差是非常重要的统计参数，它们可以用来描述和比较不同的数据集。

在实际应用中，通过计算样本的均值和方差，我们可以估计总体的均值和方差。

此外，正态分布还具有一些特殊的性质，例如68-95-99.7规则，它可以帮助我们对数据进行推断和预测。

拓展：除了均值和方差，正态分布还有一个用于描述分布形态的参数，即标准差(σ)。

标准差是方差的平方根，它具有与方差相同的单位，可以度量数据离均值的平均距离。

标准差越大，数据点相对于均值的离散程度就越大。

标准差和方差的关系是：σ = √(σ^2)。

除了单峰正态分布(n(μ,σ^2))，还有一些其他类型的正态分布。

例如，双峰正态分布具有两个峰值，可以描述具有两个主要模式的数据集。

多峰正态分布可以具有多个峰值，适用于描述具有多个主要模式的数据集。

此外，还存在偏态正态分布，其中数据在分布中不对称地倾斜。

这些不同类型的正态分布通过适当选择均值和方差来描述数据的不同特征和分布形态。