小波阈值去噪法在建筑物变形监测数据处理中的应用研究
- 格式:doc
- 大小:28.50 KB
- 文档页数:4

小波阈值去噪技术研究及其在信号处理中的应用
关山;王龙山
【期刊名称】《计算机工程与设计》
【年(卷),期】2008(29)22
【摘要】阈值函数的选取以及阈值的确定是小波收缩消噪的关键问题,阐述了小波变换及小波阈值去噪的基本原理.基于噪声和信号在小波变换下表现出截然不同的性质:噪声对应的小波变换系数将随着尺度的增大迅速衰减,建立了小波收缩消噪的统一框架.在该框架下总结了各种阈值函数的形式以及阈值确定的方式,研究了它们的性能及特点.仿真实验结果表明,该方法既能有效地去除信号噪声,又能较好地保留原信号中的突变信息.
【总页数】3页(P5857-5859)
【作者】关山;王龙山
【作者单位】吉林大学,机械科学与工程学院,吉林,长春,130025;吉林大学,机械科学与工程学院,吉林,长春,130025
【正文语种】中文
【中图分类】TN911.32;TH133
【相关文献】
1.小波阈值去噪在光纤持气率计信号处理中的应用 [J], 孔令富;孔维航;解娜;李英伟
2.小波阈值去噪在FMCW雷达信号处理中的应用 [J], 陈文会;刘芹;刘小民;李喆
3.小波阈值去噪法在非稳定信号处理中的应用 [J], 吕游;王崇倡
4.小波阈值去噪技术研究及其在生物医学信号处理中的应用 [J], 赵治栋;吴涛;潘敏;陈裕泉
5.小波阈值去噪在深小孔钻削声发射信号处理中的应用 [J], 李占国; 宗姝; 史尧臣因版权原因,仅展示原文概要,查看原文内容请购买。

基于小波分解的建筑物变形监测数据处理发表时间:2018-12-17T15:48:45.783Z 来源:《防护工程》2018年第23期作者:任亚光[导读] 小波分析是最近十几年发展起来的新的信号处理技术,其在时域和频域上都可达到高的分辨率,有“数学显微镜”之称合肥市测绘设计研究院安徽省合肥市 238000摘要:小波分析是最近十几年发展起来的新的信号处理技术,其在时域和频域上都可达到高的分辨率,有“数学显微镜”之称。
利用小波滤波进行多尺度分析,对原始信号中包含的各种频率成分进行分解,去除观测序列的噪声(测量误差),提取变形监测对象的动态特性,评定观测结果的质量,在工程实践中有很高的应用价值。
关键词:小波分解;建筑物变形;监测数据处理;由于观测环境和设备等因素的影响,建筑物变形监测的数据与建筑物真实的变形量有一定的误差。
这些误差对建筑物的安全评价有一定的影响,因此需要对数据进行去噪处理,获取其准确的变形信息,以便掌握变形的情况,及时发现问题,保证工程建筑的安全。
在传统的降噪滤波方法中,需要待检测信号的先验知识(如卡曼滤波),而傅立叶变换主要对长期持续的周期性信号有效。
由于小波变换适于分析由短时高频成分和长时低频成分组成且无太多先验知识的信号,可以考虑将小波分析方法用于建筑物变形监测数据的处理之中(这里信号等同于观测数据,噪声即观测误差),去除观测误差,即可得到消噪之后的观测数据。
一、基本原理利用小波分析去噪,即是在不同尺度下作小波变换,其实质就是用不同中心频率的带通滤波器对信号进行滤波,把那些主要反映噪声频率的尺度小的小波变换去掉,即可得到质量较好的有用信号。
同时,根据被滤除的噪声信号,可以评定噪声的大小。
由于实际观测到的信号都是离散的,所以,信号处理都是用离散小波变换(DWT)。
对任一信号,离散小波变换的第1 步是将信号分为低频部分(近似部分)和高频部分(细节部分)。
近似部分代表了信号的主要特征。
第2 步对低频部分再进行相似运算(这时尺度因子已改变),并依次进行到所需要的尺度。



基于LMD的小波包去噪法在变形监测数据去噪中的应用
洪垒;蔡永春
【期刊名称】《测绘技术装备》
【年(卷),期】2024(26)1
【摘要】为了解决工程类变形监测数据受噪声干扰,无法表现变形体真实变形趋势的问题,本文在传统局部均值分解(LMD)技术的基础上引入小波包去噪法,构建新的
基于LMD的小波包去噪法。
该组合去噪法实现去噪的主要步骤是:首先,使用LMD 对原始信号进行分解,得到若干个分量,其中,信号的有用信息主要包含在低频分量中,噪声成分包含在高频分量中;其次,使用小波包去噪法对高频分量进行去噪,尽可能提取高频分量中的有用信息;最后,将去噪处理的高频分量与低频分量进行重构,得到最终去噪信号。
另外,还使用仿真信号与实测变形监测信号对本文提出的去噪方法进
行了检验。
结果表明,相较于传统的LMD去噪法与小波包去噪法,本文基于LMD的小波包去噪法得到的相关系数、信噪比更高,均方根误差更低,具有更好的去噪效果。
【总页数】6页(P93-98)
【作者】洪垒;蔡永春
【作者单位】浙江省测绘科学技术研究院;浙江省国土勘测规划有限公司杭州分公
司
【正文语种】中文
【中图分类】P258
【相关文献】
1.建筑物变形监测数据去噪的LMD方法
2.改进的小波包阈值法去噪的桥梁变形监测数据处理
3.基于小波阈值法去噪的建筑物变形监测数据处理
4.小波阈值去噪法在矿区地表变形监测数据处理中的应用
5.小波阈值去噪在侧扫雷达监测数据去噪中的应用
因版权原因,仅展示原文概要,查看原文内容请购买。
基于小波消噪的时序分析法在变形监测数据处理中的应用的开题报告一、选题背景及意义随着现代化建设的不断推进,地下工程的规模和数量也越来越大。
而地下工程的变形监测与预测是保证地下工程安全和稳定的重要手段。
在地下工程建设中,变形监测的数据是判断地下工程变形状态的重要依据。
基于小波消噪的时序分析方法是目前常用的变形监测数据处理方法之一,在地下工程变形监测领域中具有广泛的应用。
本研究拟通过对基于小波消噪的时序分析法在变形监测数据处理中的应用进行探讨,进一步深化地下工程变形监测与预测领域的研究。
二、研究目的及内容本研究的目的在于探讨基于小波消噪的时序分析法在地下工程变形监测数据处理中的应用,通过对该方法的分析和研究,可为地下工程变形监测领域的相关研究提供重要理论基础和实际应用技术。
研究内容包括:1.地下工程变形监测概述及其数据处理方法技术综述。
2.小波分析原理及其在变形监测领域中的应用。
3.基于小波消噪的时序分析法的理论及其在变形监测数据处理中的应用方法。
4.利用基于小波消噪的时序分析法对实际变形监测数据进行处理,探讨该方法在变形监测领域的应用效果。
三、研究方法及实现途径本研究采用文献调研、实例分析和计算机仿真等多种方法进行。
具体实现途径包括:收集整理相关的文献和资料;利用Matlab 等软件结合实际变形监测数据进行研究和计算机仿真。
四、预期成果及研究价值本研究预期可获得以下成果:1.系统性掌握基于小波消噪的时序分析法在地下工程变形监测数据处理中的理论基础和实际应用技术;2.对基于小波消噪的时序分析法进行分析和研究,从而为地下工程变形监测领域的相关研究提供重要理论基础和实际应用技术;3. 通过实例分析和计算机仿真等方法,探讨基于小波消噪的时序分析法在变形监测领域中的应用效果。
本研究的研究价值不仅在于深化地下工程变形监测与预测领域的研究,更在于为地下工程建设提供重要的技术保障和理论参考。
改进的小波包阈值法去噪的桥梁变形监测数据处理冯立朋;朱军桃;熊东旭;王炯;程胜【摘要】本文采用改进的小波包去噪方法对桥梁的变形监测数据进行去噪分析.研究了改进的小波包去噪三种不同阈值函数的去噪方法,分别从最优小波基的选取、最大尺度的确定、阈值函数的改进等三个方面进行分析.通过实验分析和去噪后的评价指标分析,结果表明改进的小波包阈值函数去噪效果要优于硬阈值函数和软阈值函数去噪,并且其去噪效果也要优于传统的小波包去噪.因此,改进的小波包阈值函数去噪方法为在高精度的变形监测数据处理分析提供了一种新的方法.【期刊名称】《北京测绘》【年(卷),期】2018(032)003【总页数】5页(P344-348)【关键词】变形监测;数据处理;小波包去噪;阈值函数【作者】冯立朋;朱军桃;熊东旭;王炯;程胜【作者单位】桂林理工大学测绘地理信息学院,广西桂林 541006;桂林理工大学广西空间信息与测绘重点实验室,广西桂林 541006;桂林理工大学测绘地理信息学院,广西桂林 541006;桂林理工大学广西空间信息与测绘重点实验室,广西桂林541006;桂林理工大学测绘地理信息学院,广西桂林 541006;桂林理工大学广西空间信息与测绘重点实验室,广西桂林 541006;桂林理工大学测绘地理信息学院,广西桂林 541006;桂林理工大学广西空间信息与测绘重点实验室,广西桂林 541006;桂林理工大学测绘地理信息学院,广西桂林 541006;桂林理工大学广西空间信息与测绘重点实验室,广西桂林 541006【正文语种】中文【中图分类】P258;P2080 引言近几十年以来,国民经济建设高速发展,国家的各项基础建设也与时俱进,各式各样的大型桥梁工程的进入我们的视野,如杭州湾跨海大桥,胶州湾跨海大桥等。
这些桥梁在实际运营过程中不可避免地会受到各种复杂因素的影响如海风,海浪等自然条件以及桥梁的承受的荷载,都将对桥梁的正常运营产生一定的影响。
小波阈值去噪法在建筑物变形监测数据处理中的应用研究
【摘要】基于小波阈值法具有非常明显的渐进近似最优性质,可以在均方差意义下取得最优的去噪效果,利用小波阈值法去噪的技术,对一组建筑物变形监测数据进行去噪处理。
实验结果表明,小波阈值去噪合理有效,能够敏感识别观测噪声和有用信息,不需要待检测信号的先验知识,特别适合于建筑物变形监测数据处理。
【关键词】变形监测;小波分析;阈值去噪;软硬阈值折衷法;改进软硬阈值折衷法
1. 引言
(1)小波分析是最近十几年发展起来的新的信号处理技术,其在时域和频域上都可达到高的分辨率,有”数学显微镜”之称。
由于小波变换适于分析由短时高频成分和长时低频成分组成且无太多先验知识的信号,可以考虑将小波分析方法用于建筑物变形监测数据的处理之中(这里信号等同于观测数据,噪声即观测误差),去除观测误差,得到去噪后数据。
(2)在众多小波滤波方法中,阈值方法得到广泛应用。
小波阈值法是小波域去噪的主要方法之一,该方法通过选取合适的阈值,采用阈值函数对小波系数进行相应的非线性处理,在最小均方误差意义下可达到近似最优并且可取得较好的视觉效果,因而得到了深入的研究和广泛的应用。
其中选取合适的阈值函数是该方法最基本的问题之一。
2. 小波阈值法去噪的基本原理
2.11995年,Dohono D.l[3] 在小波变换的基础上提提出了阈值去噪的方法,其基本思想是,当小波系数Wj,k小于某个临界阈值时,认为这时的Wj,k主要是由噪声引起的,应该舍弃;当Wj,k大于这个临界阈值时,认为这时的小波系数主要是由信号引起的,那么就把这一部分的Wj,k直接保留下来(硬阈值方法)或者按某一个固定量向零收缩(软阈值方法),然后用新的小波系数进行小波重构得到去噪后信号。
2.2小波阈值去噪基本处理过程[4] :
(1)分解过程:选定一种小波,对信号进行N层分解。
(2)高频系数的阈值选择与量化过程:对于从第一层到第N层的每一层,选择一个阈值,并且对高频系数作用软阈值处理。
(3)重建过程:降处理后的系数通过小波重建恢复原始信号。
如何将噪声很好的分离,需要考虑选取适当的小波、确立最佳的分解层数和选取合适的阈值;阈值选取和量化是最关键的。
3. 改进的小波阈值去噪方法
3.11995年Dohono D.L和Johnstone教授在小波变换的基础上提出了阈值去噪的方法(wavelet shrinkage)。
他们先后提出了硬阈值、软阈值[5] 和几乎硬阈值[6] 等阈值处理函数。
万永福,袁震东[7] 分析了各种传统的阈值处理方法,提出了一个一般化的带有参数α阈值策略分数幂模型。
3.2软、硬阈值方法虽然在实际工程中得到了比较广泛的应用,并且也取得了较好的效果,但其本身还存在一些缺陷:在硬阈值函数处理过程中,估计小波系数的连续性比较差,当利用估计小波系数重构所得的信号可能会产生一些振荡;而软阈值函数虽然整体连续性较好,但软阈值法对所有大于阈值的系数共同做了收缩,估计的小波系数和原来的小波系数有恒定的偏差,这也影响了去噪后的信号和原始信号的逼近误差。
3.3为此根据上述两种方法的不足之处做了一些改进,人们提出了软硬阈值折衷法。
软硬阈值折衷法相对传统的阈值函数去噪,通过调整α 的值可以达到不同程度的去噪效果。
但是它只是软硬阈值的折衷,重构的信号会引起一定程度的振荡。
因此根据上述软硬阈值折衷法的不足,本文对软硬阈值折衷发进行了改进,改进的阈值函数为:
3.4从式(2)和式(3)可以说明,当a1时式(1)接近软阈值函数;而当a∞时,式(1)接近硬阈值函数,由此可知,改进的阈值函数是介于软、硬阈值函数之间的,并且可以通过调整α和β的值来得到不同的去噪效果。
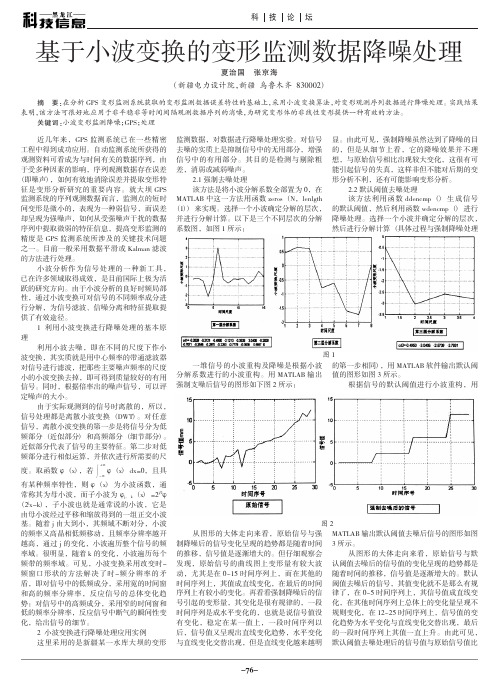
3.5该改进的软硬阈值折衷法如图1所示:
可以看出函数f(x)是以y=x 为渐近线的,也就是说,改进的阈值函数是以m,b= wm,b为渐近线的,wm,b 越大,m,b 就逐渐接近wm,b ,这样减小了软阈值函数处理后m,b与wm,b之间有恒定的偏差。
另外,无论α、β取何值改进的阈值函数都具有连续性,并且参数α取值空间要比在软硬阈值折衷法中更大。
所以改进的软硬阈值较传统的阈值函数要更加优越。
4. 仿真实验
4.1在变形监测工作中,监测数据是典型的时变信号,它反映的被监测对象的变化趋势。
如果存在观测噪声,观测值就不精确,这样会降低对建筑物变形预测的精确度。
因此得到准确的原始信号对建筑物变形预测至关重要。
4.2但是要准确的获取原始信号,仅保留低频部分还是不行的,因为是,原始信号中本身也可能包含有一些高频信息,如果简单地将所有分解出来的高频分一概去掉,将导致去噪后信号失真。
解决的办法就是选择合理阈值以及阈值策略
函数来决定哪些部分保留,哪些部分除去,然后用保留下来的小波分解系数进行重构运算。
图2五种阈值函数去噪效果比较
4.3在某市地铁站基坑开挖影响范围内有一9层民用建筑,为了监测其倾斜变形情况,设立倾斜观测点,采用TOPCOM全站仪以小角度法进行。
其中的Q-18点用于监测建筑物沿垂直于基坑轴线方向的倾斜。
规定:偏向基坑时的倾斜率为正,偏离基坑时的倾斜率为负值。
Q-18点的倾斜观测数据见表1。
显然这些数据可以视为离散信号序列,从而作为原始信号。
通过MATLAB软件,以含有噪声的倾斜观测数据作为信号进行仿真实验,选用分层阈值选取方式,使用软、硬阈值函数以及软硬阈值折衷法进行仿真实验,实验中采用的小波基是sym4小波,分解层数为3层。
结果如图2所示。
4.4从图2可以看到,以上方法去噪后的信号较原信号光滑了很多,而且可以明显观察到累积倾斜值的变化趋势。
但是四种阈值函数去噪的效果有所不同,从图上看硬阈值函数去噪后信号产生了一些振荡与其它两种阈值函数去噪效果相比不够光滑。
改进阈值函数具有连续性,减小了重构所得的信号可能产生一些振荡,使信号变得光滑(见表2)。
4.5从表2可以看出,改进的几种阈值函数去噪后的信号的信噪比[9]都要比软阈值法去噪后信号的信噪比大,这是因为这几种函数可以减小了软阈值函数处理后m,b与wm,b之间有恒定的偏差。
所以这几种阈值函数去噪后信号的信噪比要比软阈值函数大,而且去噪后信号也比硬阈值去噪后要光滑。
也就是说,它们是软。
硬阈值的折衷。
但是α和β 值不是唯一的,如果在一定的范围内选取合适的α和β,其效果会更加明显。
5. 结论
(1)基于小波阈值法去噪,不但能够有效滤除原始观测值中的高频噪声,而且可以从被高频噪声淹没的观测值中提取有用信息,得到关于被观测对象的长期变化趋势,尤其适合建筑物变形监测的数据处理。
(2)阈值以及阈值策略函数的选取是小波阈值去噪方法的关键,这也是小波去噪的核心步骤,它直接影响了小波去噪效果的优劣。
不同的阈值选取和阈值函数都会产生不同的去噪效果。
本文给出的改进的阈值函数是传统的软、硬阈值函数的一种折衷,可以调节系数产生不同的去噪效果。
(3)小波基的构造与选择必须符合具体情况,计算实例表明,使用sym4小波对变形监测数据进行去噪,能够得到满意结果。
因此小波阈值法去噪方法在变形监测数据处理方面有很大的应用价值。
参考文献
[1]飞思科技产品研发中心.小波分析理论与MATLAB 7实现[M].北京:电子工业出版社.2005.
[2]赵瑞珍,胡占义,胡绍海. 天体光谱信号去噪的小波域符合阈值新算法[J].2007,27(8):1647~1647.
[3]王红燕,邵玉槐,张海,齐锋光.基于小波阈值方法的电能质量扰动去噪分析[J].太远理工大学学报,2006,37(2)185~187.
[4] 懂长虹,小波分析工具箱原理与应用[M].北京:国防工业出版社.2003.
[5]王红燕,邵玉愧,张海,齐锋光.基于小波阈值方法的电能质量扰动去噪分析[J].太远理工大学学报,2006,37(2):185~187.
[6]赵瑞珍,胡占义,胡绍海.天体光谱信号去噪的小波域复合阈值新算法[J].光谱学与光谱分析,2007,27(8):1644~1647.
[7]万福永,袁震东.小波收缩策略的广义分数幂模型[J].华东师范大学学报(白然科学版),2001,8(3):164~167.
[8]赵瑞珍,宋国乡.一种基于小波变换的白噪声消噪方法的改进[J].西安电子科技大学学报,2000,27(5):619~622.
[9]程忠良,贾振红,覃锡忠. 基于改进阈值的低压电力线信道中的小波去噪方法[J].电视技术,2009,49(8):18~21.。