【湘教版】初一七年级数学上册《2.5 第3课时 整式的加减》习题(点击出答案)
- 格式:ppt
- 大小:1.26 MB
- 文档页数:7

七年级上册《数学》整式的加减练习题2.1 第1课时单项式一、能力提升1.下列结论正确的是()A.a是单项式,它的次数是0,系数为1B.π不是单项式C.是一次单项式D.-是6次单项式,它的系数是-2.已知是8次单项式,则m的值是()A.4B.3C.2D.13.3×105xy的系数是,次数是.4.下列式子:①ab;②-;③;④-a2+a;⑤-1;⑥a-,其中是单项式的是.(填序号)5.写出一个含有字母x,y的五次单项式:.6.观察下面的单项式:a,2a2,4a3,8a4,…,根据你发现的规律,第8个式子是.7.某学校到文体商店买篮球,篮球单价为a元,买10个以上(包括10个)按8折优惠.用单项式填空:(1)购买9个篮球应付款元;(2)购买m(m≥10)个篮球应付款元.8.若单项式(k-3)x|k|y2是五次单项式,则k=.9.观察下列各数,用含n的单项式表示第n个数.-2,-4,-6,-8,-10,…,.二、创新应用10.观察下列单项式:-x,3x2,-5x3,7x4,…,-37x19,39x20,…,回答下列问题:(1)这组单项式的系数的规律是什么?(2)这组单项式的次数的规律是什么?(3)根据上面的归纳,你可以猜想出第n个单项式是什么吗?(4)请你根据猜想,写出第2020,2021个单项式.答案一、能力提升1.D a是单项式,次数、系数均为1,所以A错;因为π是单独的一个数,所以π是单项式,所以B错;的分母中含有字母,无法写成数字与字母的积,所以不是单项式,所以C错;对于D项,它的系数为-,次数为2+3+1=6,所以D正确.2.C由单项式的次数的定义,得2m+3+1=8,将A,B,C,D四选项分别代入验证知C为正确答案.3.3×105;2.4.①②⑤.5.-x4y(答案不唯一).6.128a8.7.(1)9a.(2)0.8ma.8.-3;由题意,得|k|+2=5,且k≠3,解得k=-3.9.-2n;-2,-4,-6,-8,-10,这些数都是负数,且都是偶数,因此第n个数为-2n.二、创新应用10.解:(1)这组单项式的系数的符号规律是(-1)n,系数的绝对值规律是2n-1,故系数的规律是(-1)n(2n-1).(2)次数即x的指数的规律是从1开始的连续自然数.(3)第n个单项式是(-1)n(2n-1)x n.(4)第2020个单项式是4039x2020,第2021个单项式是-4041x2021.2.1 第2课时多项式一、能力提升1.下列说法正确的是()A.多项式ax2+bx+c是二次多项式B.四次多项式是指多项式中各项均为四次单项式C.-ab2,-x都是单项式,也都是整式D.-4a2b,3ab,5是多项式-4a2b+3ab-5中的项2.如果一个多项式是五次多项式,那么它任何一项的次数()A.都小于5B.都等于5C.都不小于5D.都不大于53.一组按规律排列的多项式:a+b,a2-b3,a3+b5,a4-b7,……其中第10个式子是()A.a10+b19B.a10-b19C.a10-b17D.a10-b214.若x n-2+x3+1是五次多项式,则n的值是()A.3B.5C.7D.05.-3x2y-2x2y2+xy-4的最高次项为.6.若一个关于a的二次三项式的二次项系数为2,常数项和一次项系数都是-3,则这个二次三项式为.7.多项式的二次项系数是.8.如图(1)(2),某餐桌桌面可由圆形折叠成正方形(图中阴影部分表示可折叠部分).已知折叠前圆形桌面的直径为am,折叠成正方形后其边长为bm.如果一块正方形桌布的边长为am,并按图(3)所示把它铺在折叠前的圆形桌面上,那么桌布垂下部分的面积是多少?如果按图(4)方式把这块桌布铺在折叠后的正方形桌面上呢?并求当a=2,b=1.4时它们的面积大小(π取3.14).9.四人做传数游戏,甲任取一个数传给乙,乙把这个数加1传给丙,丙再把所得的数平方后传给丁,丁把所得的数减1报出答案,设甲任取的一个数为a.(1)请把游戏最后丁所报出的答案用整式的形式描述出来;(2)若甲取的数为19,则丁报出的答案是多少?二、创新应用10.如图,观察点阵图形和与之对应的等式,探究其中的规律:(1)请在④和⑤后面的横线上分别写出相应的等式:(2)通过猜想,写出与第n个图形相对应的等式.答案一、能力提升1.C.2.D;多项式的次数指的是次数最高项的次数,故一个五次多项式次数最高项的次数为5.3.B;根据多项式排列的规律,字母a的指数是按1,2,3,…的正整数排列,故第10个式子应为a10.字母b的指数是按1,3,5,7,…的奇数排列,故第10个式子应为b19.中间的符号第1个式子是正,第2个式子是负,这样正、负相间,故第10个式子应为a10-b19.4.C;由题意,得n-2=5,解得n=7.5.-2x2y2;6.2a2-3a-3.7.=-,二次项为,故二次项系数为.8.解:m2;(a2-b2)m2;2.04m2.当a=2,b=1.4时,a2-a2=22-×22=4-3.14=0.86(m2),a2-b2=22-1.42=2.04(m2).9.解:(1)由甲传给乙变为a+1;由乙传给丙变为(a+1)2;由丙传给丁变为(a+1)2-1.故丁所报出的答案为(a+1)2-1.(2)由(1)知,代入a=19,得399.二、创新应用10.解:(1)④4×3+1=4×4-3.⑤4×4+1=4×5-3.(2)4(n-1)+1=4n-3.2.2 第1课时合并同类项一、能力提升1.下列各组式子为同类项的是()A.x2y与-xy2B.0.5a2b与0.5a2cC.3b与3abcD.-0.1m2n与nm22.若-2a m b2m+n与5a n+2b2m+n可以合并成一项,则m-n的值是()A.2B.0C.-1D.13.若x a+2y4与-3x3y2b是同类项,则(a-b)2021的值是()A.-2021B.1C.-1D.20214.已知a=-2021,b=,则多项式3a2+2ab-a2-3ab-2a2的值为()A.1B.-1C.2021D.-5.若2x2y m与-3x n y3的和是一个单项式,则m+n=.6.若关于字母x的整式-3x2+mx+nx2-x+3的值与x的值无关,则m=,n=.7.把(x-y)和(x+y)各看作一个字母因式,合并同类项3(x+y)2-(x-y)+2(x+y)2+(x-y)-5(x+y)2=.8.合并下列各式的同类项:(1)-2x2-8y2+4y2-5x2-5x+5x-6xy;(2)3x2y-4xy2-3+5x2y+2xy2+5.9.已知-2a m bc2与4a3b n c2是同类项,求多项式3m2n-2mn2-m2n+mn2的值.10.先合并同类项,再求值:(1)7x2-3+2x-6x2-5x+8,其中x=-2;(2)3x-4x3+7-3x+2x3+1,其中x=-2.二、创新应用11.有这样一道题:“当a=0.35,b=-0.28时,求多项式7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3的值.”有一名同学指出,题目中给出的条件“a=0.35,b=-0.28”是多余的,他的说法有没有道理?为什么?答案一、能力提升1.D2.A;∵-2a m b2m+n与5a n+2b2m+n可以合并成一项,∴m=n+2,则m-n=2.故选A.3.C;由同类项的定义,得a+2=3,2b=4,解得a=1,b=2.所以(a-b)2021=(1-2)2021=(-1)2021=-1.4.A;把多项式合并同类项,得原式=-ab,当a=-2021,b=时,原式=1.5.5;2x2y m与-3x n y3的和是一个单项式,说明2x2y m与-3x n y3是同类项,即m=3,n=2,故m+n=5.6.1;3;算式的值与x的值无关,说明合并同类项后,所有含x项的系数均为0.-3x2+mx+nx2-x+3=(-3+n)x2+(m-1)x+3,则m=1,n=3.7.0.8.解:(1)-2x2-8y2+4y2-5x2-5x+5x-6xy=(-2-5)x2+(-8+4)y2+(-5+5)x-6xy=-7x2-4y2-6xy.(2)3x2y-4xy2-3+5x2y+2xy2+5=(3+5)x2y+(-4+2)xy2+(-3+5)=8x2y-2xy2+2.9.解:由同类项定义,得m=3,n=1.3m2n-2mn2-m2n+mn2=(3-1)m2n+(-2+1)mn2=2m2n-mn2.当m=3,n=1时,原式=2×32×1-3×12=18-3=15.10.解:(1)原式=(7-6)x2+(2-5)x+(8-3)=x2-3x+5,当x=-2时,原式=(-2)2-3×(-2)+5=15.(2)原式=-2x3+8,当x=-2时,原式=-2×(-2)3+8=24.二、创新应用11.解:他的说法有道理.因为原式=(7+3-10)a3+(-6+6)a3b+(3-3)a2b=0,所以原式的值与a,b的值无关.即题目中给出的条件“a=0.35,b=-0.28”是多余的.2.2 第2课时去括号一、能力提升1.三角形的第一条边长是(a+b),第二条边比第一条边长(a+2),第三条边比第二条边短3,这个三角形的周长为()A.5a+3bB.5a+3b+1C.5a-3b+1D.5a+3b-12.如果a-3b=-3,那么5-a+3b的值是()A.0B.2C.5D.83.今天数学课上,老师讲了多项式的加减,放学后,小明回到家拿出课堂笔记复习老师课上讲的内容,他突然发现一道题:(x2+3xy)-(2x2+4xy)=-x2【】.【】处被钢笔水弄污了,则此处中的一项是()A.-7xyB.7xyC.-xyD.xy4.化简(3x2+4x-1)+(-3x2+9x)的结果为.5.若一个多项式加上(-2x-x2)得到(x2-1),则这个多项式是.6.已知a-b=3,c+d=2,则(b+c)-(a-d)的值为.7.某轮船顺水航行了5h,逆水航行了3h,已知船在静水中的速度为akm/h,水流速度为bkm/h,则轮船顺水航行的路程比逆水航行的路程多.8.先化简,再求值:(1)(x2-y2)-4(2x2-3y2),其中x=-3,y=2;(2)a-2[3a+b-2(a+b)],其中a=-21,b=1000.9.已知A=2x2+3xy-2x-1,B=-x2+kxy-1,且A+B的值与y无关,求k的值.10.观察下列各式:①-a+b=-(a-b);②2-3x=-(3x-2);③5x+30=5(x+6);④-x-6=-(x+6).探索以上四个式子内的括号的变化情况,思考它和去括号法则有什么不同?利用你探索出来的规律,解答下面的题目:已知a2+b2=5,1-b=-2,求-1+a2+b+b2的值.二、创新应用11.有理数a,b,c在数轴上的位置如图所示,试化简|a-b|-|c-a|+|b-c|-|a|.答案一、能力提升1.B;三角形的周长为a+b+(a+b+a+2)+(a+b+a+2-3)=a+b+a+b+a+2+a+b+a+2-3=5a+3b+1.2.D;由a-3b=-3,得-(a-3b)=3,即-a+3b=3.因此5-a+3b=5+3=8.3.C.4.13x-1;(3x2+4x-1)+(-3x2+9x)=3x2+4x-1-3x2+9x=13x-1.5.2x2+2x-1;(x2-1)-(-2x-x2)=x2-1+2x+x2=2x2+2x-1.6.-1;由a-b=3,可得a-b的相反数为-3,即-(a-b)=-3,即-a+b=-3,因此(b+c)-(a-d)=b+c-a+d=(-a+b)+(c+d)=-3+2=-1.7.(2a+8b)km轮船在顺水中航行了5(a+b)km,在逆水中航行了3(a-b)km,因此轮船顺水航行的路程比逆水航行的路程多5(a+b)-3(a-b)=5a+5b-3a+3b=(2a+8b)km.8.解:(1)原式=-x2+y2.当x=-3,y=2时,原式=-.(2)原式=2b-a.当a=-21,b=1000时,原式=2021.解:A+B=(2x2+3xy-2x-1)+(-x2+kxy-1)=2x2+3xy-2x-1-x2+kxy-1=x2+(3+k) xy-2x-2.因为A+B的值与y无关,所以3+k=0,解得k=-3.10.解:因为a2+b2=5,1-b=-2,所以-1+a2+b+b2=-(1-b)+(a2+b2)=-(-2)+5=7.二、创新应用11.解:由题意知a-b<0,c-a>0,b-c<0,a<0,因此原式=-(a-b)-(c-a)-(b-c)-(-a)=-a+b-c+a-b+c+a=a.2.3 第3课时整式的加减一、能力提升1.已知一个多项式与3x2+9x的和等于3x2+4x-1,则这个多项式是()A.-5x-1B.5x+1C.-13x-1D.13x+12.化简-3x-的结果是()A.-16x+B.-16x+C.-16x-D.10x+3.如图①,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“”图案,如图②所示,再将剪下的两个小长方形拼成一个新的长方形,如图③所示,则新长方形的周长可表示为()A.2a-3bB.4a-8bC.2a-4bD.4a-10b4.小明在复习课堂笔记时,发现一道题:=-x2-xy+y2,括号处被钢笔弄污了,则括号处的这一项是()A.y2B.3y2C.-y2D.-3y25.已知a3-a-1=0,则a3-a+2020=.6.多项式(4xy-3x2-xy+x2+y2)-(3xy-2x2+2y2)的值与无关.(填“x”或“y”)7.若a2+ab=8,ab+b2=9,则a2-b2的值是.8.若2x-y=1,则(x2+2x)-(x2+y-1)=.9.先化简,再求值:2(a2b+ab2)-(2ab2-1+a2b)-2,其中a=-,b=-2.10.计算:(1)3(a2-4a+3)-5(5a2-a+2);(2)3x2-.11.规定一种新运算:a*b=a+b,求当a=5,b=3时,(a2b)*(3ab)+5a2b-4ab的值.二、创新应用12.扑克牌游戏.小明背对小亮,让小亮按下列四个步骤操作:第一步:分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌现有的张数相同;第二步:从左边一堆拿出两张,放入中间一堆;第三步:从右边一堆拿出一张,放入中间一堆;第四步:左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.这时,小明准确地说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是多少?并说明你的理由.13.小黄做一道题“已知两个多项式A,B,计算A-B”.小黄误将A-B看作A+B,求得结果是9x2-2x+7.若B=x2+3x-2,请你帮助小黄求出A-B的正确答案.答案一、能力提升1.A;由题意,得(3x2+4x-1)-(3x2+9x)=3x2+4x-1-3x2-9x=-5x-1.2.B.3.B;所得新长方形的长为a-b,宽为a-3b,则其周长为2[(a-b)+(a-3b)]=2(2a-4b)=4a-8b.4.C;=-x2+3xy-y2+x2-4xy-()=-x2-xy-y2-()=-x2-xy+y2,故括号处的这一项应是-y2.5.2021;由a3-a-1=0,得a3-a=1,整体代入得a3-a+2020=1+2020=2021.6.x;因为(4xy-3x2-xy+x2+y2)-(3xy-2x2+2y2)=4xy-3x2-xy+x2+y2-3xy+2x2-2y2=-y2, 所以多项式的值与x无关.7.-1;a2+ab-(ab+b2)=a2+ab-ab-b2=a2-b2=8-9=-1.8.2;当2x-y=1时,(x2+2x)-(x2+y-1)=x2+2x-x2-y+1=2x-y+1=1+1=2.故答案为2.9.解:原式=2a2b+2ab2-2ab2+1-a2b-2=a2b-1,当a=-,b=-2时,原式=×(-2)-1=×(-2)-1=--1=-.10.解:(1)3(a2-4a+3)-5(5a2-a+2)=3a2-12a+9-25a2+5a-10=-22a2-7a-1.(2)3x2-=3x2-5x+x-3-2x2=x2-x-3.11.解:原式=a2b+3ab+5a2b-4ab=(1+5)a2b+(3-4)ab=6a2b-ab.当a=5,b=3时,原式=6×52×3-5×3=450-15=435.二、创新应用12.解:设第一步每堆各有x张牌;第二步左边有(x-2)张牌,中间有(x+2)张牌,右边有x张牌;第三步左边有(x-2)张牌,中间有x+2+1=x+3张牌,右边有(x-1)张牌;第四步中间有x+3-(x-2)=x+3-x+2=5张牌,因此中间一堆牌现有的张数是5.13.解:因为A+B=9x2-2x+7,B=x2+3x-2,所以A=9x2-2x+7-(x2+3x-2)=9x2-2x+7-x2-3x+2=8x2-5x+9,所以A-B=8x2-5x+9-(x2+3x-2) =8x2-5x+9-x2-3x+2=7x2-8x+11.。

初中数学湘教版七年级上册第二章2.5整式的加法和减法练习题一、选择题1.如果M是五次多项式,N是五次多项式,那么M+N一定是()A. 十次多项式B. 次数不高于五的整式C. 五次多项式D. 次数不低于五的整式2.计算2a−3a,结果正确的是()A. −1B. 1C. −aD. a3.一个多项式加上ab−3b2等于b2−2ab+a2,则这个多项式为()A. 4b2−3ab+a2B. −4b2+3ab−a2C. 4b2+3ab−a2D. a2−4b2−3ab4.如果2x a+1y与x2y b−1是同类项,那么ab的值是()A. 12B. 32C. 1D. 35.若A=x2−2xy+y2,B=x2+2xy+y2,则4xy=()A. B−AB. B+AC. A−BD. 2A−2B6.化简13(9x−3)−2(x+1)的结果是()A. 2x−2B. x+1C. 5x+3D. x−37.若x+y=2,z−y=−3,则x+z的值等于()A. 5B. 1C. −1D. −58.下列运算正确的是()A. 3x+2x=5x2B. 3x−2x=xC. 3x⋅2x=6xD. 3x÷2x=23二、填空题9.计算(x+a)(2x−1)的结果中不含关于字母x的一次项,则a=______.10.若单项式−12x2y a与−2x b y5的和仍为单项式,则这两个单项式的和为______.11.若单项式2x2y m与−13x n y4可以合并成一项,则n m=______.12.若代数式M=5x2−2x−1,N=4x2−2x−3,则M,N的大小关系是M______N(填“>”“<”或“=”)三、计算题13.已知代数式A=x2+3xy+x−12,B=2x2−xy+4y−1(1)当x=y=−2时,求2A−B的值;(2)若2A−B的值与y的取值无关,求x的值.14.已知代数式A=x2+xy−2y,B=2x2−2xy+x−1(1)求2A−B;(2)若2A−B的值与x的取值无关,求y的值.四、解答题15.郊区某中学学霸父母只要有时间就陪孩子一起完成家庭作业,在某天晚上,勤芬准备完成作业时:化简(x2+7x+6)−(7x+8x2−4).发现系数“”印刷不清楚.(1)她把“”猜成3,请你化简:(3x2+7x+6)−(7x+8x2−4);(2)爸爸说:“你猜错了,我看了标准答案的结果是常数.”请你通过计算说明来帮助勤芬得到原题中“”是几.16.有这样一道题:“当a=0.35,b=−0.28时,求多项式7a3−6a3b+3a2b+3a3+6a3b−3a2b−10a3的值.”小明说:本题中a=0.35,b=−0.28是多余的条件;小强马上反对说:这不可能,多项式中每一项都含有a和b,不给出a,b的值怎么能求出多项式的值呢?你同意哪名同学的观点?请说明理由.答案和解析1.【答案】B【解析】解:如果M是五次多项式,N是五次多项式,那么M+N一定是次数不高于五的整式,故选:B.根据整式的加减法则判断即可.此题考查了整式的加减,熟练掌握运算法则是解本题的关键.2.【答案】C【解析】解:2a−3a=−a,故选:C.根据合并同类项法则合并即可.本题考查了合并同类项法则的应用,能熟记合并同类项法则的内容是解此题的关键.3.【答案】A【解析】解:∵一个多项式加上ab−3b2等于b2−2ab+a2,∴这个多项式是(b2−2ab+a2)−(ab−3b2)=b2−2ab+a2−ab+3b2=4b2−3ab+a2,故选:A.先根据题意列出算式,再去括号,合并同类项即可.本题考查整式的加减的应用,解此题的关键是能根据题意列出算式.4.【答案】A【解析】【分析】此题考查了同类项的概念,代数式求值,属于基础题,掌握同类项所含字母相同,并且相同字母的指数也相同,是解答本题的关键.根据同类项:所含字母相同,并且相同字母的指数也相同,可得出a、b的值,然后代入求值.【解答】解:∵2x a+1y与x2y b−1是同类项,∴a+1=2,b−1=1,解得a=1,b=2.∴ab =12.故选A.5.【答案】A【解析】解:∵A=x2−2xy+y2,B=x2+2xy+y2,∴B−A=(x2+2xy+y2)−(x2−2xy+y2)=x2+2xy+y2−x2+2xy−y2=4xy,则4xy=B−A.故选:A.将A与B代入B−A中,去括号合并得到结果为4xy,可得出4xy=B−A.此题考查了整式的加减运算,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握法则是解本题的关键.6.【答案】D【解析】【分析】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.原式去括号合并即可得到结果.【解答】解:原式=3x−1−2x−2=x−3,故选:D.7.【答案】C【解析】解:∵x+y=2,z−y=−3,∴(x+y)+(z−y)=2+(−3),整理得:x+y+z−y=2−3,即x+z=−1,则x+z的值为−1.故选:C.已知两等式左右两边相加即可求出所求.此题考查了整式的加减,熟练掌握运算法则是解本题的关键.8.【答案】B【解析】解:(A)原式=5x,故A错误;(C)原式=6x2,故C错误;(D)当x≠0时,原式=32,故D错误;故选:B.根据整式的运算法则即可求出答案.本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.9.【答案】12【解析】解:(x+a)(2x−1)=2x2+2ax−x−a=x2+(2a−1)x−a由题意得2a−1=0则a=12,故答案为:12首先利用多项式的乘法法则计算:(x+a)(2x−1),结果中不含关于字母x的一次项,即一次项系数等于0,即可求得a的值.此题考查整式的化简求值,注意先化简,再进一步代入求得数值即可.10.【答案】−52x2y5【解析】解:∵单项式−12x2y a与−2x b y5的和仍为单项式,∴b=2,a=5,∴−12x2y a−2x b y5=−12x2y5−2x2y5=−52x2y5.故答案是:−52x2y5.根据题意可知单项式−12x2y a与−2x b y5是同类项,故此可求得a、b的值,然后再合并这两个单项式即可.本题主要考查的是同类项、合并同类项,掌握同类项的定义是解题的关键.11.【答案】16【解析】解:由题意得,n=2,m=4,则n m=16,故答案为:16.根据同类项的定义计算.本题考查的是合并同类项,要掌握同类项的概念,会辨别同类项,并准确地掌握判断同类项的两条标准:带有相同系数的代数项;字母和字母指数.12.【答案】>【解析】解:M−N=5x2−2x−1−(4x2−2x−3),=5x2−2x−1−4x2+2x+3,=x2+2>0,∴M>N,故答案为:>.首先计算出M、N的差,再分析差的正负性可得答案.此题主要考查了整式的加减,关键是注意去括号时符号的变化.13.【答案】解:(1)2A−B=2(x2+3xy+x−12)−(2x2−xy+4y−1)=2x2+6xy+2x−24−2x2+xy−4y+1=7xy+2x−4y−23.当x=y=−2时,原式=7×(−2)×(−2)+2×(−2)−4×(−2)−23=9.(2)∵2A−B=7xy+2x−4y−23=(7x−4)y+2x−23.由于2A−B的值与y的取值无关,∴7x−4=0∴x=4.7【解析】(1)先化简多项式,再代入求值;(2)合并含y的项,因为2A−B的值与y的取值无关,所以y的系数为0.本题主要考查整式的加减−化简求值,给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.14.【答案】解:(1)2A−B=2(x2+xy−2y)−(2x2−2xy+x−1)=2x2+2xy−4y−2x2+2xy−x+1=4xy−x−4y+1;(2)∵2A−B=4xy−x−4y+1=(4y−1)x−4y+1,且其值与x无关,∴4y−1=0,.解得y=14【解析】(1)把A与B代入2A−B中,去括号合并即可得到结果;(2)由2A−B与x取值无关,确定出y的值即可.此题主要考查了整式的加减运算,正确合并同类项是解题关键.15.【答案】解:(1)原式=3x2+7x+6−7x−8x2+4=−5x2+10;(2)设看不清的数字为a,则原式=(ax2+7x+6)−(7x+8x2−4)=ax2+7x+6)−7x−8x2+4=(a−8)x2+10;因为结果为常数,所以a−8=0,解得:a=8即原题中的数为8.【解析】(1)直接去括号进而合并同类项得出答案;(2)直接利用合并同类项法则进而得出未知数的系数为零进而得出答案.此题主要考查了整式的加减,正确合并同类项是解题关键.16.【答案】解:我同意小明的观点.理由如下:7a3−6a3b+3a2b+3a3+6a3b−3a2b−10a3=(7+3−10)a3+(−6+6)a3b+(3−3)a2b=0,所以a=0.35,b=−0.28是多余的条件,故小明的观点正确.【解析】根据整式的加减混合运算法则把原式化简,根据化简结果解答.本题考查的是整式的化简求值,掌握整式的加减混合运算法则是解题的关键.。

整式的加法和减法(第3课时)(30分钟50分)一、选择题(每题4分,共12分)7a2 -7ab ( )A.(3a2 -ab +7) -(4a2 +6ab +7)B.(3a2 -ab +7) -(-4a2 -6ab +7)C.(3a2 -ab +7) -(-4a2 -6ab -7)D.(3a2 -ab +7) -(-4a2 +6ab +7)【解析】选D.因为(3a2 -ab +7) -(4a2 +6ab +7) =3a2 -ab +7-4a2 -6ab -7 = -a2 -7ab;(3a2 -ab +7) -(-4a2 -6ab +7)=3a2 -ab +7 +4a2 +6ab -7 =7a2 +5ab;(3a2 -ab +7) -(-4a2 -6ab -7)=3a2 -ab +7 +4a2 +6ab +7=7a2 +5ab +14;(3a2 -ab +7) -(-4a2 +6ab +7)=3a2 -ab +7 +4a2 -6ab -7=7a2 -7ab.【变式训练】假设A =x2 -2xy +y2,B =x2 +2xy +y2,那么以下各式运算结果等于4xy的是( )【解析】选C.因为A =x2 -2xy +y2,B =x2 +2xy +y2,所以 -A = -x2 +2xy -y2,所以 -A +B = -x2 +2xy -y2 +x2 +2xy +y2 =4xy,所以运算结果等于4xy的是 -A +B.2.有一道题是一个多项式减去xy -2yz +3zx,小红误当成了加法算式,所得答案是2yz -3zx +2xy,那么正确的答案应该是( )【解题指南】解答此题根本思路(1)先确定这个多项式(被减数).(2)再按原来的要求算出正确的答案.【解析】选B.被减数应为2yz -3zx +2xy -(xy -2yz +3zx)=2yz -3zx +2xy -xy +2yz -3zx=4yz -6zx +xy,正确的答案应为:4yz -6zx +xy -(xy -2yz +3zx)=4yz -6zx +xy -xy +2yz -3zx=6yz -9zx.【互动探究】如果原来是加法运算,被小红当成了减法运算,那么正确的答案应该是什么?【解析】根据题意,正确的答案应该是2yz -3zx +2xy +2(xy -2yz +3zx)=2yz -3zx +2xy +2xy -4yz +6zx= -2yz +3zx +4xy.3.下面四个整式中,不能表示图中阴影局部面积的是( )A.(x +3)(x +2) -2xB.x(x +3) +6C.3(x +2) +x22 +5x【解析】选D.A、大长方形的面积为:(x +3)(x +2),空白处小长方形的面积为:2x,所以阴影局部的面积为(x +3)(x +2) -2x,故正确;B、阴影局部可分为长为x +3,宽为x和长为3,宽为2的两个长方形,它们的面积分别为x(x +3)和3×2 =6,所以阴影局部的面积为x(x +3) +6,故正确;C、阴影局部可分为一个长为x +2,宽为3的长方形和边长为x的正方形,那么它们的面积为:3(x +2) +x2,故正确.二、填空题(每题4分,共12分)4.多项式x -y减去 -x +3y的差是.【解析】依题意得:(x -y) -( -x +3y) =2x -4y.答案:2x -4y【易错提醒】当多项式相减时,要在后面的多项式前面加上括号,此题不要出现x -y +x +3y =2x +2y这样的错误.【变式训练】一个多项式减去( -3 +x -2x2)得到x2 -1,这个多项式是.【解析】设这个多项式为M,那么M =x2 -1 +( -3 +x -2x2)=(1 -2)x2 +x -4= -x2 +x -4.答案: -x2 +x -45.如果A =3m2 -m +1,B =2m2 -m -7,且A -B +C =0,那么C = .【解析】因为A -B +C =0,所以C =B -A =(2m2 -m -7) -(3m2 -m +1)=2m2 -m -7-3m2 +m -1= -m2 -8.答案: -m2 -85a +4b,剪下一局部围成一个长为a宽为b的长方形,那么这根铁丝还剩下.【解析】剪下的长方形的周长为2(a +b),那么这根铁丝还剩下5a +4b -2(a +b) =3a +2b.答案:3a +2b三、解答题(共26分)7.(8分):A -2B =7a2 -7ab,B =-4a2 +6ab +7.(1)求A.(2)假设|a +1| +(b -2)2 =0,计算A的值.【解析】(1)由题意得:A =2(-4a2 +6ab +7) +7a2 -7ab=-8a2 +12ab +14 +7a2 -7ab= -a2 +5ab +14.(2)因为|a +1| +(b -2)2 =0,所以a = -1,b =2,所以A = -( -1)2 +5×( -1)×2 +14 =3.8.(8分)三角形的周长为a,它的一边长是周长的,另一边长是周长与4的差的一半,求第三边的长.【解析】依题意得,第|一边长为,第二边长为(a -4),所以第三边长为a - -(a -4)=a - - a +2 = a +2.【培优训练】9.(10分)有这样一道题: "先化简,再求值:(7a3-6a3b +3a2b) -(-3a3-6a3b +3a2b)-10a3 +2,其中a = -3,b = -0.39.〞小宝说:此题中 "a = -3,b = -”是多余的条件;小玉马上反对说:这个多项式中每一项都含有a和b,不给出a,b的值怎么能求出多项式的值呢?你同意哪名同学的观点?请说明理由.【解析】同意小宝的观点.因为(7a3-6a3b +3a2b) -( -3a3-6a3b +3a2b) -10a3 +2=7a3-6a3b +3a2b +3a3 +6a3b-3a2b-10a3 +2=2,所以此题中a = -3,b = -0.39是多余的条件.。

第3课时整式加减的应用与化简求值60座客车的人数是(A . 75—15x知识要点分类练知识点1整式加减的应用1.多项式 x 2 — y 2减去x 2 + y 2所得的差是( A . — 2y 2 2y 2 C . 2x 2—2x 22. 一个整式与x 2— y 2的和是x 2+ y 2,则这个整式是()22x2B . 2y3. 2 —2x 2D . — 2y已知三角形的周长为 3m — n ,其中两边的和为 m + n — 4,则此三角形第三边的长为2m — 4 B . 2m — 2n —42m — 2n + 4D . 4m — 2n + 44.将多项式x 3— 3x 2y + 3xy 2— y 3写成两个二项式的差,下列写法错误的是()3322(x — y )— (3x y — 3xy )QO2Q(x 3 + 3xy 2)— (3x 2y + y 3),322 |3、(x — 3xy )— (3xy + y ) (3xy 2—3x 2y)—(y 3 —X 3)5.某校组织若干名师生进行社会实践活动. 人无座位;若租用60座的客车,则可少租用若学校租用 45座的客车x 辆,则余下151辆,且最后一辆还没坐满,那么乘坐最后一辆135— 15x 135—60x6.五个连续偶数中,中间一个是n ,则这五个数的和是C. 75+ 15x知识点2整式的化简求值& 当x=- 1时,多项式一2x—(2x + 1)的值为()A . 3B 1 C. 1 D 59. 当a =—1, b = 1 时,(a3—b3) —(a3—3a2b+ 3ab2—b3)的值是( )A. 0B. 6C.—6D. 92 210. 当a = —3 时,2a —(1 —2a + a ) —(—1 + 3a —a ) = __ .11. 先化简,再求值:2 3 3(1) (4 a+ 3a —3 + 3a ) + (a —4a ),其中a=—2;(2) 2(2x—3y)—(3x+ 2y+ 1),其中x= 2, y = —0.5;7. 一根铁丝的长为5a + 4b,剪下一部分围成一个长为a,宽为b的长方形,则这根铁丝剩下的长度为 ________2 2 2 2(3)5(3 a b — ab) — 4( — ab + 3a b),其中 a =- 1, b = 2.12.若 A = 3a 2— 5a + 6,B = 2a 2— 5a + 3,贝V A 与 B 的大小关系是()A . A =B B . A > BC . A V BD .不能确定13.已知 a — b = 4, c + d = 3,则(b +c) — (a — d)的值为()A . — 1B . 1C . — 5D . 1514 .长方形的一边长等于 3a + 2b ,与其相邻的另一边长比它大 a — b ,那么这个长方形的周长是()A . 14a + 6b规律方】去综合练B . 7a + 3bC . 10a+ 10bD . 12a + 8b15 .若a2+ 2b2= 5,则多项式(3a2—2ab+ b2)—(a2—2ab—3b2)的值是_________16. 有这样一道题:“求3a2—4a2b+ 3ab+ 4a2b—ab+ a2—2ab 的值,其中a=—1, b= 才”小明同学把b = *错写成了b= —2,但他计算的结果是正确的,请你通过计算说明这是怎么回事.217. 已知A = 2a —a, B = —5a + 1.⑴化简:3A—2B + 2;1⑵当a=—寸时,求3A —2B + 2的值.18. 一个三角形的一边长为 a + b,另一边比这条边长b,第三条边比这条边短a—b.(1) 求这个三角形的周长;(2) 若a = 5, b= 3,求三角形的周长.拓广探究创新练淖知满令1 a b 1 a b19.定义为二阶行列式,规疋匕的运算法则为=ad —be,那么当x= 11 c d I c dx+ 1x—2时,二阶行列式的值为()3—5A . 7B. —7C. 1 D . —120.把四张形状、大小完全相同的小长方形卡片(如图2 —5-3①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示. 求图②中两块阴影部分的周长和.①教师详解详析I. A 2.B3 . C [解析]根据题意,得(3m—n) —(m+ n —4) = 3m—n—m—n + 4= 2m —2n+ 4.故选 C.4. C5. B [解析]总人数为45x+ 15,则最后一辆车的人数为45x+ 15—60(x—2) = 135 —15x. 故选B.6. 5n7.3a+ 2b8. A [解析]原式=—2x—2x —1 = —4x —1.当x = —1 时,原式=—4X (—1) —1 = 3.9. B10. —32 3 3 3 2II. 解:(1)原式=4a + 3a —3+ 3a + a —4a = —a + 3a + 5a—3.当a=—2时,原式=—(—2)3+ 3X (—2)2+ 5X ( —2) — 3 = 7.(2) 原式=4x—6y—3x—2y —1 = x—8y—1,将x= 2, y= —0.5 代入,得原式=x—8y— 1 = 2 —8 X (—0.5) —1 = 2 + 4— 1 = 5.2 2 2 2 2 2(3) 原式=15a b—5ab + 4ab —12a b= 3a b—ab ,当a=—1, b = 2 时,原式=6+ 4 = 10.12. B [解析]用取差法比较大小:A—B = (3a2—5a + 6) —(2a2—5a + 3) = a2+ 3>0,所以A> B.13. A 14.A 15. 1016. 解:原式化简后的结果为4a2.1 1因为化简后的结果与b的取值无关,所以小明同学把b= 1错写成b= —1,计算结果仍是正确的.2 2 217. 解:(1)3A—2B + 2 = 3(2a —a)—2( —5a+ 1) + 2 = 6a —3a+ 10a—2+ 2 = 6a + 7a.(2)当a= —2时,3A —2B+ 2= 6 X - 2 + 7X —2 =- 2.18. 解:(1)这个二角形的周长是(a+ b) + (a + 2b)+ [a + b —(a —b)] = a+ b+ a + 2b+ a +b —a+ b = 2a+ 5b.(2)当a = 5, b= 3 时,三角形的周长=2a + 5b = 2 X 5+ 5 X 3= 25.x + 1 x—219 B [解析] =—5(x+ 1) —3(x—2)=—5x—5 —3x+ 6 =—8x+ 1.3 —5当x= 1时,原式=—8 + 1 = —7•故选B.20.解:设小长方形的长为a,宽为b,则上面阴影部分的周长为2(n —a+ m —a),下面阴影部分的周长为2(m —2b+ n —2b),所以阴影部分的周长和为2(n —a+ m—a) + 2(m —2b + n —2b) = 4m+ 4n —4(a + 2b). 因为a+ 2b= m,所以4m+ 4n —4(a+ 2b)= 4n.即两块阴影部分的周长和为4n.。
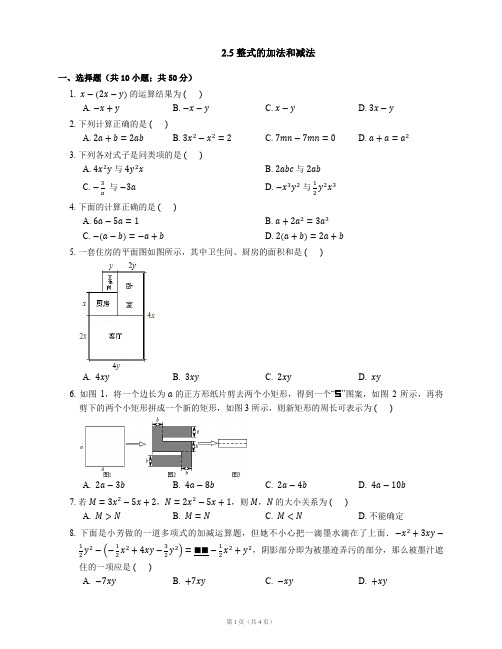
2.5 整式的加法和减法一、选择题(共10小题;共50分)1. x−(2x−y)的运算结果为 ( )A. −x+yB. −x−yC. x−yD. 3x−y2. 下列计算正确的是 ( )A. 2a+b=2abB. 3x2−x2=2C. 7mn−7mn=0D. a+a=a23. 下列各对式子是同类项的是 ( )A. 4x2y与4y2xB. 2abc与2abC. −3a 与−3a D. −x3y2与12y2x34. 下面的计算正确的是 ( )A. 6a−5a=1B. a+2a2=3a3C. −(a−b)=−a+bD. 2(a+b)=2a+b5. 一套住房的平面图如图所示,其中卫生间、厨房的面积和是 ( )A. 4xyB. 3xyC. 2xyD. xy6. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“”图案,如图2 所示,再将剪下的两个小矩形拼成一个新的矩形,如图 3 所示,则新矩形的周长可表示为 ( )A. 2a−3bB. 4a−8bC. 2a−4bD. 4a−10b7. 若M=3x2−5x+2,N=2x2−5x+1,则M,N的大小关系为 ( )A. M>NB. M=NC. M<ND. 不能确定8. 下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面.−x2+3xy−1 2y2−(−12x2+4xy−32y2)=■■−12x2+y2,阴影部分即为被墨迹弄污的部分,那么被墨汁遮住的一项应是 ( )A. −7xyB. +7xyC. −xyD. +xy9. 要使多项式6x+5y−3+2ky+4k不含y的项,则k的值是 ( )A. 0B. 25C. 52D. −5210. 在两个形状、大小完全相同的大长方形内,分别互不重叠地放入四个如图③的小长方形后得图①,图②,已知大长方形的长为a,两个大长方形未被覆盖部分分别用阴影表示,则图①阴影部分周长与图②阴影部分周长的差是 ( )(用a的代数式表示)A. −aB. aC. −12a D. 12a二、填空题(共10小题;共50分)11. 化简a−(−2b+c)=.12. 在括号内填上适当的项.(1)a+b−c=+=−=a−;(2)a−b−c=−=a−=+−c.13. 无论字母a,b取何值,代数式−13ab2+56ab2−12ab2−2的值总是.14. m−[n−2m−( )]=4n−2m.在横线处填空.15. 已知有理数a,b互为相反数,c,d互为倒数,∣m∣=4,则2a−7cd−m+2b的值为.16. 当b=时,式子2a+ab−5的值与a无关.17. 若∣x+y+3∣+(xy−2)2=0,则(4x−2xy+3)−(2xy−4y+1)的值为.18. 已知代数式(2x2+ax−y+6)−(2bx2−3x+5y−1).① 当a=,b=时,此代数式的值与字母x的取值无关;② 在①的条件下,多项式3(a2−2ab−b2)−(4a2+ab+b2)的值为.19. 如果3x2y m与−2x n−1y3是同类项,那么m+n=.20. 设−1≤x≤2,则∣x−2∣−12∣x∣+∣x+2∣的最大值与最小值之差为三、解答题(共5小题;共65分)21. 先化简,再求值:2x+7+3x−2,其中x=2.22. 有一个多项式,当减去2x2−3x+7时,某学生因把“减去”误认为“加上”,得到结果为5x2−2x+4.那么按照正确的运算要求,最后结果应该是什么?23. 化简求值:(x2y−2xy2)−[(−3x2y2+2x2y)+(3x2y−2xy2)],其中x=2,y=−1.24. 如图,在数轴上点A,B,C表示的数分别为−2,1,6,点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.Ⅰ则AB=,BC=,AC=;Ⅱ点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B 和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.请问:BC−AB的值是否随着运动时间t的变化而改变?若变化,请说明理由;若不变,请求其值;Ⅲ由第(1)小题可以发现,AB+BC=AC.若点C以每秒3个单位长度的速度向左运动,同时,点A和点B分别以每秒1个单位长度和每秒2个单位长度的速度向右运动.请问:当运动时间t在0∼1秒之间时,AB,BC,AC之间是否存在类似于(1)的数量关系?请说明理由.25. 若关于x,y的多项式x m−1y3+x3−m y∣n−2∣+x m−1y+x2m−3y∣n∣+m+n−1合并同类项后得到一个四次三项式,直接写出m,n的值(所有指数均为正整数).答案第一部分1. A2. C3. D4. C5. B6. B7. A8. C9. D 10. C 第二部分 11. a +2b −c12. (1)a +b −c ;−a −b +c ;−b +c ;(2)−a +b +c ;b +c ;a −b 13. −2 14. 5n −5m 15. −11 或 −3 16. −2 17. −1818. ① −3;1 ② 8 19. 6 20. 1 第三部分21. 2x +7+3x −2 =5x +5, 当 x =2 时, 原式=5×2+5=15.22. x 2−4x +10.23. 原式=x 2y −2xy 2−(−3x 2y 2+2x 2y +3x 2y −2xy 2)=x 2y −2xy 2+3x 2y 2−2x 2y −3x 2y +2xy 2=3x 2y 2−4x 2y. 当 x =2,y =−1 时,原式=3×22×(−1)2−4×22×(−1)=12+16=28.24. (1) 3;5;8(2) BC =5t −2t +5,AB =t +2t +3,BC −AB =(5t −2t +5)−(t +2t +3)=2,故 BC −AB 的值不会随着时间 t 的变化而改变. (3) AB +BC =AC .由题意得,AB =t +3,BC =5−5t ,AC =8−4t , 所以 AB +BC =(t +3)+(5−5t )=8−4t =AC . 25. m =2,n =1 或 3.。

整式的加法和减法(第3课时)(30分钟50分)一、选择题(每小题4分,共12分)1.下列哪个式子的计算结果为7a2-7ab ( )A.(3a2-ab+7)-(4a2+6ab+7)B.(3a2-ab+7)-(-4a2-6ab+7)C.(3a2-ab+7)-(-4a2-6ab-7)D.(3a2-ab+7)-(-4a2+6ab+7)【解析】选D.因为(3a2-ab+7)-(4a2+6ab+7)=3a2-ab+7-4a2-6ab-7=-a2-7ab;(3a2-ab+7)-(-4a2-6ab+7)=3a2-ab+7+4a2+6ab-7=7a2+5ab;(3a2-ab+7)-(-4a2-6ab-7)=3a2-ab+7+4a2+6ab+7=7a2+5ab+14;(3a2-ab+7)-(-4a2+6ab+7)=3a2-ab+7+4a2-6ab-7=7a2-7ab.【变式训练】若A=x2-2xy+y2,B=x2+2xy+y2,则下列各式运算结果等于4xy的是( ) A.A+B B.A-BC.-A+BD.-A-B【解析】选C.因为A=x2-2xy+y2,B=x2+2xy+y2,所以-A=-x2+2xy-y2,所以-A+B=-x2+2xy-y2+x2+2xy+y2=4xy,所以运算结果等于4xy的是-A+B.2.有一道题是一个多项式减去xy-2yz+3zx,小红误当成了加法算式,所得答案是2yz-3zx+2xy,那么正确的答案应该是( )A.-6yzB.6yz-9xzC.4yz-6xz+4xyD.3xy【解题指南】解答本题基本思路(1)先确定这个多项式(被减数).(2)再按原来的要求算出正确的答案.【解析】选B.被减数应为2yz-3zx+2xy-(xy-2yz+3zx)=2yz-3zx+2xy-xy+2yz-3zx=4yz-6zx+xy,正确的答案应为:4yz-6zx+xy-(xy-2yz+3zx)=4yz-6zx+xy-xy+2yz-3zx=6yz-9zx.【互动探究】如果原来是加法运算,被小红当成了减法运算,那么正确的答案应该是什么? 【解析】根据题意,正确的答案应该是2yz-3zx+2xy+2(xy-2yz+3zx)=2yz-3zx+2xy+2xy-4yz+6zx=-2yz+3zx+4xy.3.下面四个整式中,不能表示图中阴影部分面积的是( )A.(x+3)(x+2)-2xB.x(x+3)+6C.3(x+2)+x2D.x2+5x【解析】选D.A、大长方形的面积为:(x+3)(x+2),空白处小长方形的面积为:2x,所以阴影部分的面积为(x+3)(x+2)-2x,故正确;B、阴影部分可分为长为x+3,宽为x和长为3,宽为2的两个长方形,它们的面积分别为x(x+3)和3×2=6,所以阴影部分的面积为x(x+3)+6,故正确;C、阴影部分可分为一个长为x+2,宽为3的长方形和边长为x的正方形,则它们的面积为:3(x+2)+x2,故正确.二、填空题(每小题4分,共12分)4.多项式x-y减去-x+3y的差是.【解析】依题意得:(x-y)-(-x+3y)=2x-4y.答案:2x-4y【易错提醒】当多项式相减时,要在后面的多项式前面加上括号,本题不要出现x-y+x+3y=2x+2y这样的错误.【变式训练】一个多项式减去(-3+x-2x2)得到x2-1,这个多项式是.【解析】设这个多项式为M,则M=x2-1+(-3+x-2x2)=(1-2)x2+x-4=-x2+x-4.答案:-x2+x-45.如果A=3m2-m+1,B=2m2-m-7,且A-B+C=0,则C= .【解析】因为A-B+C=0,所以C=B-A=(2m2-m-7)-(3m2-m+1)=2m2-m-7-3m2+m-1=-m2-8.答案:-m2-86.一根铁丝的长为5a+4b,剪下一部分围成一个长为a宽为b的长方形,则这根铁丝还剩下.【解析】剪下的长方形的周长为2(a+b),则这根铁丝还剩下5a+4b-2(a+b)=3a+2b.答案:3a+2b三、解答题(共26分)7.(8分)已知:A-2B=7a2-7ab,B=-4a2+6ab+7.(1)求A.(2)若|a+1|+(b-2)2=0,计算A的值.【解析】(1)由题意得:A=2(-4a2+6ab+7)+7a2-7ab=-8a2+12ab+14+7a2-7ab=-a2+5ab+14.(2)因为|a+1|+(b-2)2=0,所以a=-1,b=2,所以A=-(-1)2+5×(-1)×2+14=3.8.(8分)三角形的周长为a,它的一边长是周长的,另一边长是周长与4的差的一半,求第三边的长.【解析】依题意得,第一边长为,第二边长为(a-4),所以第三边长为a--(a-4)=a--a+2=a+2.【培优训练】9.(10分)有这样一道题:“先化简,再求值:(7a3-6a3b+3a2b)-(-3a3-6a3b+3a2b)-10a3+2,其中a=-3,b=-0.39.”小宝说:本题中“a=-3,b=-0.39”是多余的条件;小玉马上反对说:这个多项式中每一项都含有a和b,不给出a,b的值怎么能求出多项式的值呢?你同意哪名同学的观点?请说明理由.【解析】同意小宝的观点.因为(7a3-6a3b+3a2b)-(-3a3-6a3b+3a2b)-10a3+2=7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3+2=2,所以本题中a=-3,b=-0.39是多余的条件.教师个人研修总结在新课改的形式下,如何激发教师的教研热情,提升教师的教研能力和学校整体的教研实效,是摆在每一个学校面前的一项重要的“校本工程”。
温馨提示:此套题为Word 版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
第3课时整式的加减回|分层作业基础达标〜1. [2018秋拱墅区期末]下列各式去括号正确的是()A. - 2 Qx—y = —x—2yB. —0.5(1 —2x)= —0.5+ xC. —(2x2—x+ 1)= —2x2—x+1D. 3(2x—3y)= 6x—3y2. [2018秋平定县期末]计算6a2—5a + 3与5a2+ 2a—1的差, 结果正确的是()A. a2—3a+ 4B. a2—3a + 2C. a2—7a+ 2D. a2—7a + 43. _________________________________________ 计算:(5a2+ 2a)—4(2 + 2a2)= ________________________________ .4. 计算:(1)3(3a2—2ab) —2(4a2—ab);(2)2x—[2(x + 3y)—3(x—2y)].5. [2018秋老河口市期中]先化简再求值:2x^ —Rxy2—2(x『+12x2y)],其中x=2,y= —2.「Bill •繼力握升「6. [2018 秋和平区期末]已知A= 3x2+ 3y2—5xy, B= 2xy—3y2 + 4x2.(1) 化简:2B —A;(2) 已知一a|x—2|b2与3ab y是同类项,求2B —A的值.7. 已知代数式(2x2+ ax—y+ 6)—(2bx2—3x—5y—1)的值与字母1 1 、x无关,求代数式3a3—2b2— 2 — 3a3+ b2的值.8.如图2-5-2, —只蚂蚁从点A沿数轴向右爬2个单位长度到3达点B,若点A表示的数是a=-2,设点B表示的数为b.(1) 求b的值;(2) 化简:2(a2- 2ab) - [2a2- 2b+ 2(ab + b)],再求值.图2-5-2参考答案1. B2.D 2.- 2a2+ 2a-84. (1)a2—4ab (2)2x- 12y5. 6x2y-xy2,原式=-5・6. (1)9xy—9y2+ 5x2(2)当x= 1, y= 2 时,2B-A=- 13;当x =2, y= 2 时,2B- A = 62.7. - 2118. (1)b= 2 (2)-8ab,原式=6.关闭Word 文档返回原板块。