当前位置：文档之家 › 第三章2-薄膜干涉分解

第三章2-薄膜干涉分解

  • 格式：ppt
  • 大小：1.23 MB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

第三章 干涉

第三章 干涉

两波到达P点的相位差为：
2 1 2 ( n2 r2 n1r1 ) ( 01 02 ) 2 c c ( 2 c , n1 , n2 ) 1 2
( r2 r1 ) ( 01 02 )
1、相位差

2
频率相等，振动方向（光矢量 E ）平行、相
位差恒定。
3、波动的特征 “干涉”和“衍射”现象是波动的重要特征。
四、相干叠加与非相干叠加
1、两简谐振动的合成
1 A t 1 ) 1 cos(
2 A2 cos( t 2 )
1 2 A cos( t )
'
dx r2 r1 d sin d tan D
考虑到移动方向相反
D x s R
例1：用白光做光源观察双缝干涉，缝间距为d，试 求能观察到的清晰可见光谱的级次。白光波长范围 390—750nm。
例2：一双缝实验中，两缝间距为0.15mm，在1.0m处 测得第一级和第十级暗纹之间距离为36mm。试求所 用单色光的波长。
——分波阵面法
(3) 劳埃德镜
P'
P
s1
d
s2
M
L
d'
半波损失 ：光由光疏介质射向光密介质时， 反射光相位突变π 。
三、干涉条纹的移动
零级条纹在P0 光源移动δs 条纹移动δx
R2 r2 R1 r 1
R1 R2 (r1 r2 )
傍轴, 小角度下:
R1 R2 d sin ' ds d tan R
n2 n

2
Q

2 L 2h n 2 n1 sin 2 i1

第三章 干涉3

第三章 干涉3

v L0 ct c(t1 t 2 ) l c
2
将干涉仪沿垂直轴旋转90o，时间差或光程差改变了正 负号，相对于观察点光程差有一个改变量：
v d (L) 2L0 2l c
2
在旋转中应该观察到干涉条纹的移动。
光源为钠黄光，=590nm，地球公转和自转的速度估计 为v=30km/s，臂长l=11m，可以推算条纹移动N=0.4。但 是没有观察到条纹移动。 零的结果最终导致人们放弃了伽利略变换，寻求与相对 性原理和麦克斯韦电磁理论和谐统一的新时空变化，产生 了狭义相对论。
例（1）迈克尔逊干涉仪可用来测量单色光波，当 M2移动距离 d 0.322mm 时，测得单色光的干涉条 纹移过N＝1024条，试求单色光的波长。（2）在 M2前，插一透明薄片n＝1.632 ，可观察到150条干 涉条纹向一方移动，所用单色光的波长=5000A， 求薄片厚度。
解：
2 o 2d 2 0.322 103 6289 A N 1024
§3-4 薄膜干涉（二） ——等倾干涉
等倾干涉 （薄膜厚度均匀） 1. 两条光线的光程差
面光源
n2 (ab bc) n1 ad 2 2n2 e cos
2

s
P L 1 2E
i d i
n
1
2e n n sin i
2 2 2 1 2

2
e a
c n n 2 1
n
1
b

e ab bc , cos (2k 1) , k 0,1, 暗纹 2 ad ac sin i 2etg sin i
注意： • Half – wave loss • 透镜不产生附加光程差

薄膜干涉 讲解

薄膜干涉 讲解

1
2
,
2 nd ( 2 k 2 1 )
2
2
2 k1 1 2 7 2 k 2 1 1 5
即： 10 k1 5 14 k2 7
求得：
k1 3 ,
k2 2
2 k1 1 d 1 673nm 4n
例题 4-7：
白光垂直入射在肥皂膜上，观察反射光，在可见光中对λ1= 600 nm 的光 有一干涉极大，而对λ2 = 450 nm的光有一干涉极小。肥皂膜折射率为 n = 1.33，求满足以上条件时，肥皂膜的最小厚度。
解： ⑴ 由条纹突起的方向可判断是凹槽。 ⑵ 由下图：
a sin h b sin sin sin a h b 2
a
h
a
b

2

2b
α
b a
h
dk
解得：
dk+1
h
例题4-11：
当牛顿环装置中的透镜与玻璃板间充以某种液体时，牛顿环中第 10个亮 环的直径由 1.40 cm 变为 1.27 cm ，求这种液体的折射率。
r 2 R 2 ( R d )2 2 Rd d 2 2 Rd
r 2 Rd ( L
牛顿环仪

2
)R
明环半径
暗环半径
r
1 ( k )R 2
r
kR
O点处：d = 0、 Δ L = λ /2 —→ 暗斑
以O为圆心的一 组同心圆环
牛顿环可应用于测量透镜曲率半径、检查表面平整度等。 例：测量透镜的曲率半径 R 。 设测得 k、k+1 级暗环的半径为 rk、rk+m，则
d n

3-02 薄膜干涉(一)——等厚条纹

3-02 薄膜干涉(一)——等厚条纹

n
h
第三章：干涉装置 光场的时空相干性 § 2 薄膜干涉（一）——等厚条纹
2.6 薄膜的颜色、增透膜和高反膜 薄膜的颜色：干涉导致不同波长光的反射率不同。 增透膜：
n1 < n < n 2 nh = λ 4 , n1 n n2
例： n1 = 1,
3λ 4 ,
n1 n 2 时完全消光
→ n 0 = 1 . 23
2.2 薄膜表面的等厚条纹（i固定，h变化） 光程差计算：
Q
i1
C
n
A
i
B
P
h
Δ L ( P ) = ( QABP ) − ( QP ) = ( QA ) − ( QP ) + ( ABP ) Δ L ( P ) ≈ 2 nh cos i
第三章：干涉装置 光场的时空相干性 § 2 薄膜干涉（一）——等厚条纹
2 nh cos i = conL ) = − 2 nh sin i δ i + 2 n cos i δ h = 0
第三章：干涉装置 光场的时空相干性 § 2 薄膜干涉（一）——等厚条纹
2.5 等厚干涉条纹的观测方法及倾角的影响 ii)反衬度下降： 眼睛瞳孔限制扩展光源 参与干涉的区域。光源 不同处的 i 不同， h 越 大，反衬度越低。
rk2+ m − rk2 R= mλ
由于半波损失，中心时暗纹。
rk
DP k2 = CP k2 − CD 2 rk2 = R 2 − ( R − h k ) 2 = 2 Rh k − h k2
第三章：干涉装置 光场的时空相干性 § 2 薄膜干涉（一）——等厚条纹
2.5 等厚干涉条纹的观测方法及倾角的影响 严格的等厚干涉要求点光源、正入射。但扩展光源、斜入 射，用眼睛也能观察到干涉现象。主要是眼睛的瞳孔对光 束进行了限制，只是干涉的结果会受到一定的影响。 i) 条纹偏离等厚线： 干涉条纹：

第三节薄膜干涉

第三节薄膜干涉

《大学物理》
教师：
胡炳全
《大学物理》
教师：
胡炳全
L 2ne / 2 k
k 1对应的薄膜厚度最小
emin
emin

4n
无半波损失时,增反膜的 最小厚度:

2n
《大学物理》
教师：
胡炳全
增透膜的最小厚度与增反膜情况正好相反(如下表):
最小厚度 有半波损 无半波损 失 失 λ/4n λ/2n 增反膜
增透膜 λ/2n λ/4n
《大学物理》
教师：
胡炳全
第三节 薄膜干涉
一、薄膜干涉及其分类： 光线经过薄膜的两个 界面反射后在入射光一侧 发生的干涉,或透射光与 经过反射的透射光在入射 光的另一侧发生的干涉称 为薄膜干涉.前者反射光 (薄膜)干涉，后者叫透射 光(薄膜）干涉. 薄膜干涉发生的位置,可以 在薄膜的上下两个表面附近,也 可以在其它任何地方.通常我们 考虑的是发生在薄膜表面附近 的等厚干涉. P
由三角形AOO’，可得该处干涉的 光程差与半径r的关系为：
R ( R e) r
2 2
2
r e r e 2R 2R
2 2 2
nr L {0, / 2} R
干涉条纹一定是圆环，因为r相同， 厚度相同，光程差相同：
《大学物理》
教师：
胡炳全
•牛顿环干涉明纹和暗纹的半径（有半波损）
nr 由L / 2 k , 可得 : R
2
(2k 1) R r明 2n
nr 1 由L / 2 (k ) , 可得 : R 2
2
kR 空气中 r暗 kR n
牛顿环干涉 中心处为暗 纹（斑）

光的干涉1-2(简)

光的干涉1-2(简)

试 件 标准件
出现的 位置
课
堂
讨
论
劈尖干涉的应用 ——检验平面的平整度
例 3.4（P145） 试根据干涉条纹弯曲方向判断工件变形是凹还是凸？ 并求出纹路深度h 。 分析：
(1) 凹凸判断
(2) 深度计算
(参P145146 ) 试 件
标准件
例3.5 （P146） 把金属丝夹在两块平玻璃间形成劈尖。如测得金属 丝和棱边间距离为D=28.88mm，用波长λ=589.3nm 的钠黄光垂直照射时，测得30条明纹间的总距离为 4.295mm。求金属丝直径d。 待测工件 解： 由图示几何关系可知 d = D tg α D sinα 因条纹间距 而
课
堂
讨
论
例3.6（P149） 用波长为 的单色光观察等倾干涉条纹，视场中 心为一亮斑。外面围以若干圆环。若慢慢增大薄 膜厚度，则看到的干涉圆环会有什么变化？ 分析： 由 2e n 2 sin 2 i 2 k , (k 1,2,3,) 2k 1 , (k 0,1,2,)


e
B
2
2ne cos

2
3
4
二、薄膜干涉分析 (分振幅干涉) 2. 分析——光以入射角 i 入射 2ne cos
2
∵ sin i n sin n 1 - cos
2
S

n

·
i
A
1
D
2
C
sin i n (1 cos ) n2 cos2 n2 sin2 i

反射光1
反射光2
e
2e

2

高二物理竞赛薄膜干涉等厚条纹PPT(课件)


（2）检测平板玻璃表面的光洁度 有半波损
（1）这是一个近似公式 （1）中心条纹的级次低， （3）薄膜的厚度不均匀 （1）中心条纹的级次低，
（4）满足n1 n n2或 n1 n n2 时
有半波损 L(P) 2nh cos i 0 / 2
（5）有无半波损只影响条纹的绝对 若已知入射光的波长： ，
4）薄膜干涉的分类 等厚条纹和等倾条纹
2．等厚条纹
1）厚度不均匀薄膜的光程差
L(P) (QABP) (QP)
(QA) (QP) (ABP)
(QA) (QP)_____(CP) n1__A__P_ sin i1 n AP sin i
Q
i1 C
n1
Ai P h n
n(2h tan i)sin i 2nhsin2 i / cos i
第三章 干涉装置和光场的时空相干性
§1、薄膜干涉等厚条纹 （3）检测楔形薄膜交楞的位置
边缘条纹密集。
（4）判断平板平移方向和平移量
1．薄膜干涉是分振幅干涉 透明介质分界面多次反射光或
边缘条纹密集。
透明介质分界面多次反射光或
表面的干涉条纹称为等厚条纹。
1）分振幅干涉的定义 （1）这是一个近似公式
（2）条纹定位于薄膜的表面附近
(ABP) 2(AB) 2nh / cosi
B
n2
L(P) 2nh cosi
2）讨论
（1）这是一个近似公式
（3）薄膜的厚度不均匀
（2）干涉区域位于薄膜表面附近
若已知入射光的波长： ，
（3） i 是折射角，不是入射角。 （1）点光源产生的平行光垂直入射到薄
（4）空气层厚度变化， 由此可以确定等厚干涉条纹的形状
rk2 kR0 或 rk kR0

第三章 光的干涉和干涉仪-2


加强
根据具体 情况而定
1
2 L 3
( k 1, 2,L )
n2 n1
M1 M2
P
r
(2k 1) 2
减弱
n1
i
A
2
D
2
n2
n1
C
d
E 4 F 5
( k 0,1, 2, L )
B
透射光的光程差 t n2 BC CE n1 EF 2n2 d cos 2
明纹
暗纹
当光程差Δ满足条件 :
极大:
2nh

极小:
2nh

2
m
2
2m 1

2
对于楔形平板，厚度相同点的轨迹是一些平行于楔棱的
等距直线，所以，楔形平板所生的等厚条纹就是一些平
行于楔棱的等距条纹.
讨论
b
n1 n
1）棱边处 h =0, 对应着
n

h
2 半波损失的又一“例证”



2n2 h sin 2


2n1h sin 2
∴ 条纹丌等间隔，中心疏，边缘密
2 反 2h n2 n12 sin 2 1 / 2 k
③、条纹级次分布: h一定时
k 反 i1 rk
k , h一定, i1 rk
R 2º相邻两环的间隔为 r rk 1 rk k 1R kR 2 k
3º复色光入射, 彩色囿环， 4º透射光不之互补 5º 动态反应 连续增加薄膜的厚度,视 场中条纹缩入。反之,冒出。 0 1 2 345…….
L D D L N 2nb b 2n

薄膜干涉2


得：
2encosFra bibliotekr(0或
2
)
相位突变，则必须 考虑半波损失，加上
(2d
n2
n2 1
s in2
i
)
(0或
2
)
附加光程差
问题：什么情况下加附加光程差？
2encosr
？
2
1) 若 n1 n n2 或 n1 n n2
折射率为“夹心饼干”型，总有一束反射光存在 “半波损失”，须加附加光程差/2
)
k (2k
1)
2
(k 1,2 ) (k 0,1,2 )
加强（明纹） 减弱（暗纹）
（1）式中各量意义以及半波损失问题
（2）干涉加强减弱与膜厚 e 、入射角 i （或 r ）有关
特殊情况 光垂直入射到薄膜上 i 0
垂直入射到薄膜的干涉条件
2ne ( ) 2
k
(k 1,2,)
(2k 1) (k 0,1,2,) 2
Δe
k 1 k 2 ek
第k级条纹对应的厚度 ek
同一级条纹对应同一膜厚，
ek
1
(2k
k
1)
2n
第k级暗条纹
4n
明纹 (k 1,2)
暗纹(k 0,1,2)
故称为等厚条纹或等厚干涉
K=0，对应e=0，为劈尖边缘，叫做边缘暗条纹 ， k=1，e=/2n——第一级暗纹下面的薄膜厚度， e=/4n——第一级明纹下面的薄膜厚度……
l
Δe
ek ek1
条纹特点： 平行、等间距、明暗交替。
注意： 在两块玻璃片接触处： e 0
应看到暗条纹，而事实正是这样，这 是“半波损失”的一个有力的证据。

第3章光的干涉2薄膜干涉

许多著名的实验都堪称科学中的艺术，如： 全息照相实验，吴健雄实验，兰姆移位实验 等等。
重要的物理思想＋巧妙的实验构思＋精湛 的实验技术 科学中的艺术
26
二、法布里-珀罗干涉仪 多光束薄膜干涉的应用
A
B
i
r CD
nd
基本装置图
原理图
主极大满足的光程差？
2n AB CD 2nd cos r m 未考虑镀膜面对相位的2影7 响
19
§6 干涉仪 一、迈克耳逊干涉仪 1. 工作原理 光束2′和1′发生干涉
补偿板G2的作用
M2 M1
2
G1 G2 M1
S
1
半透半反膜 2 1
E
无G2时的光程差： Δ 2nt 2l2 2l1
有G2时的光程差： Δ 2l2 2l1
20
• 获得等倾条纹的条件
M1、M2平行 发散光入射
§5 分振幅法双光束干涉 一、相干光束和光程差 二、等厚条纹 三、等倾条纹
1
一、相干光 束和光程差
反射光干涉
1
i
2
薄膜
ne
2ne cosr
2 sini nsinr
· S
单色
n n
反射光2 反射光1
· A e
n (设n > n )
透射光干涉
i
薄膜
ne
2
1
2necosr

m
(m
1,2,3,)
l
明纹 暗纹

•条纹疏密的变化
（反映楔角的改变） Δl 2n
变 密F
F变 疏
平 移
改变 楔角
怎么看条纹移动？ 盯住某一级 看
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
上面用的都是单色光，若用复色光（如白光） 将会看到彩色条纹 看到的级次少，为什么？
2k 1 rk R 2
例1 利用空气劈尖的等厚干涉条纹可以检测工件表面 存在的极小的凹凸不平。
在经过精密加工的工件表面上放一光学平面玻璃， 使其间形成空气劈尖，用单色光垂直照射玻璃表面
在显微镜下观察干涉条纹。 试根据干涉条纹弯曲的方向， 说明工件表面是凹还是凸？ 并证明深度可用下式求的。
2 2 2

2
k
( 2k 1)

2
减弱
k 0,1,2,...
三. 等倾干涉
1. 等倾干涉现象 当 d 常数 薄膜为厚度均匀的
S●
n1 n2
1
L
●
P
n1
n2 n1
i D
A r
2
i
3 C 4 E
r
d
5
B
平面膜
干涉条件：
2d n2 n1 sin i
2 2 2

2
r
d
r 2R d
2
明环： 2d k k = 1, 2, … 2 2k 1 第k个明环半径 rk R 2
r2 d 2R
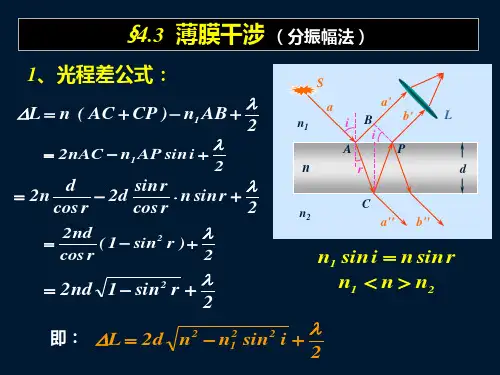
光程差：
2d
r2 d 2R
o

2

① ②
R
r
d
(k
暗环：
2d ( 2k 1) 2 2
= 0, 1, 2, …)
rk
2k 1 R 0.03 2
rk 5
2(k 5) 1 R 2
0.046
R 1.03
k一定, d i rk

• 膜厚变化时，条纹的移动：
o
i
r环
i
P
S
i i 1 2 n n > n n
L
讨论 • 条纹间隔分布: 内疏外密
r
d
rk
越大条纹越密
2dn cos r

2
k
k 1,2,...
2dn sin rr k
k 1 可得相邻两条纹的角间距 r 2dn sin r
k
( 2k 1)
明纹
k 1,2,...

2
暗纹
k 0,1,2,...
o
i
r环
i
P
S
i n
·
i
L
1
2
3. 条纹特点 • 形状: 一系列同心圆环 • 条纹级次分布:
n > n n
·
r
d
• 明暗: 干涉条纹更加明亮
rk
越大条纹级次越小
• 条纹间隔分布: 内疏外密
rk
越大条纹越密
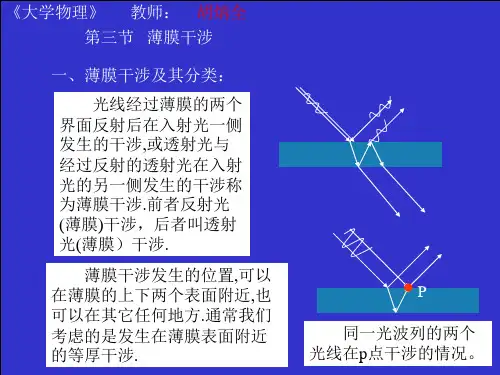
§3.6;3.7 “分振幅法”获得相干光——薄膜 干涉 一. 薄膜干涉现象 二. 薄膜干涉的一般公式 三. 等倾干涉 四. 等厚干涉
2dn2 cos r

2
k
( 2k 1)
加强 k 1,2,...

2
减弱
k 0,1,2,...
加强 k 1,2,...
2d n2 n1 sin i

明纹
2d


①
②
2 k 1,2,...
k
2
暗纹
2d ( 2k 1)
2


2
d d k d k 1
n
k 0,1,2,...
任何两个相邻的明条纹或暗条纹之间所对应的 空气层厚度之差为：
d k 1 d k
2
明纹
2d


①
②
第k个暗环半径
rk kR k
r 越大条纹越密
应用：
2 rk m
2 rk
mR
• 测透镜球面的半径R： 已知, 测 m、rk+m、rk，可得R 。 • 测波长λ： 已知R，测出m 、 rk+m、rk， 可得λ。 • 检验透镜球表面质量

标准验规 待测透镜
暗纹
上面介绍的劈尖和牛顿环的干涉现象， 都是在薄膜的反射光中看到的， 在透射光中，也同样有干涉条纹， 但这时条纹的明暗情形与反射时恰好相反， 在接触处为明纹（为什么）。
b h a2
a
b
a
b
d k 1
b a h dk
h
解： 干涉条纹弯曲说明工件表面不平， 因为k 级干涉条纹各点都相应于同一气隙厚度， 如果条纹向劈尖棱的一方弯曲，由式
2 2 说明该处气隙厚度有了增加，可判断该处为下凹 h
2d

(2k 1)


2
a b
a h b2
例2、用波长为λ的平行单色光垂直照射图中所示装置，下半部 分为一圆柱形凹面，观察空气薄膜上下表面反射光形成的等厚 干涉条纹，计算各级暗纹的位置并在装置下方的方框内画出相 应的暗条纹的大致位置（要表示出它们的形状，条数和疏密）。
解:
7 4
玻璃 空气
等厚干涉 形状：直条纹 条数：8条暗纹
暗纹条件：
2dn (2k 1) 2 2
k = 0,1,2, …
7 d 4
7 k 2
k 3
d=0处是暗纹
解:
等厚干涉 形状：直条纹 条数：8条暗纹 暗纹条件：
2d (2k 1) 2 2
2.
牛顿环
①
②
在一块光平的玻璃片B上，
放一曲率半径R 很大的
平凸透镜A， 在A 、 B之间形成一劈形空气薄膜 当垂直入射的单色平行光透过平凸透镜后， 在空气薄膜的上、下表面发生反射， 这两束光是相干光， 它们在透镜下表面处相遇而发生干涉， 空气薄膜
2.
牛顿环
①
②
光程差
2d

2
k
( 2k 1)
明纹
k 1,2,...


暗纹
k 0,1,2,... 由牛顿环结构可知， 等厚线为以接触点为圆心的同心圆， 所以牛顿环干涉图样为同心的明暗相间的圆环。
接触点
d 0
2
暗斑
下面确定明、暗圆环的半径：
光程差：
2d
2 2
o

2
2

① ②
R
r R (R d ) 2 d R d 略去
7 4
k3
k 0 k 1 k 2
k 3
d=0处是暗纹
疏密（位置分布）: 外密内疏
d 0 d /2 d 3 d 2
例3 用单色光观察牛顿环，测得某一明环的直径为 3.00mm，它外面第五个明环的直径为4.60mm, 平凸透镜的半径为1.03m，求此单色光的波长。
解：
明环的级次为k
2 k 1,2,...
k
2
d d k d k 1 2d ( 2k 1) k 0,1,2,... 2 2
暗纹

n
d k 1 d k

2
任何两个相邻的明条纹或暗条纹之间的距离
d k 1 d k θ 越小，干涉条纹愈疏， l sin 2 sin θ 越大，干涉条纹愈密。