频率选择表面(学习笔记)
- 格式:doc
- 大小:71.00 KB
- 文档页数:5

频率选择表面单元频率选择表面是一种特殊的电路板,用于在射频(无线电频率)电路中选择或过滤特定的频率。
频率选择表面通常包含一个具有不同电学性质的局部尺度结构,可以通过控制这些结构来实现所需的频率选择。
这种结构可以是互连电缆、电容器和电感器等电子元件,也可以是印在陶瓷板上的金属图案。
频率选择表面通常使用于天线、收发机、阻尼器、滤波器、功率放大器等电路设计中。
它们被广泛应用于移动通信、无线电交通、卫星通信、雷达、航天器等领域,因为这些领域的要求都需要能够对频率进行选择和控制。
频率选择表面的原理基于阻尼器(Damping circuit)的变化,可以将选定的信号通过。
该技术基于与其余传输线不同的亚波长结构。
在频率选择表面上,所传输的波被反射和散射,并在该表面上的亚波长结构中产生了相干的干涉效应。
其中,通过改变这些结构的电学性质,可以实现所需的频率选择。
过滤器和谐振器是频率选择表面的两种主要形式。
过滤器的设计是使射频信号在特定频率范围内通过,而在其他频率下被隔离或反射。
谐振器则是在特定频率处发生共振,抑制或反射不需要的频率。
频率选择表面通常由由介电体基板和局部尺度电路图案两部分组成。
介电体材料通常使用高频率的低损耗材料,如陶瓷、聚合物等。
局部尺度电路图案是由金属、导体薄膜和电介质图案构成的。
这些局部尺度的变化是通过印刷、蒸镀、切割等技术在介电体表面上制造而成的。
在频率选择表面的制造和设计中,需要考虑的一些关键因素包括尺寸、形状、特定的电学性质、温度影响和特定频率的选择。
尺寸和形状的变化可以影响频率的选择精度和灵敏度。
特定的电学性质取决于材料的选择,可以影响频率选择的带宽和阻带深度。
温度影响也是一个关键因素,因为频率选择表面对温度的变化非常敏感。
最后,特定频率的选择将影响所需的图案尺寸和电学特性。
总的来说,频率选择表面是一种非常特殊的电路板,具有许多应用领域。
它的工作原理基于阻尼器的变化,可以选择和控制信号的频率。

频率选择表面5.3.1 设计背景频率选择表面(Frequency Selective Surface,FSS)是一种二维周期性结构,可以有效地控制电磁波的反射与传输。
目前FSS的应用十分广泛,可用于反射面天线的负反射器以实现频率复用,提高天线的利用率;也可以用于波极化器、分波数仪和激光器的“腔体镜”,以提高激光器的泵浦功率;还可以用于隐身技术,应用设计的雷达天线罩能够有效地降低雷达系统的雷达散射界面。
5.3.2 设计原理FSS是一种而为周期排列的阵列结构,本身不能吸收能量,但是却能起到滤波的作用。
通常有两种形式,以后总是贴片型,是在介质衬底层上周期性地印上规则的导体贴片单元组成金属阵列;另一种是孔径型,是在很大的金属屏上周期性开孔的周期孔径结构。
这两种结构都可以实现对电磁场的频率选择作用和极化选择作用,对于谐振情况下的入射电磁波,这两种阵列分别表现出全反射(单元为导体贴片)、全透射(单元为缝隙、孔径),它们也被分别称为带阻型FSS和带通型FSS。
频率选择表面的频率选择特性主要取决于写真单元的形式、单元的排布方式以及周围戒指的电性能。
FSS的基本结构如图5-3-1所示,上下层为介质层,中间层为金属层,金属层也可以位于介质层的上下面上。
1.基本的偶极子或缝隙形式的频率选择表面FSS的两类基本形式是导线阵列和缝隙阵列,如图5-3-2所示。
介质基板PECε1 μ1ε2 μ2图5-3-1 FSS的基本结构如图5-3-2(a )所示的谐振偶极子的阵列作为带阻滤波器,不能通行偶极子谐振频率的波,但可以通行高于和低于谐振频率的波。
与之互补的在理想导电片上的缝隙阵列,如图5-3-2(b )所示,用作带通滤波器,可通行等于缝隙谐振频率的波,但拒绝较高和较低频率的波。
两种情况的传输系数图如图5-3-3所示。
2. 其他形式的频率选择表面单元形状各种各样的FSS 单元形状都是从最基本的直偶极子单元开始的。
现在讲偶极子单元分成四类,分别为:(1) “中心连接”或“N-极子”单元。

频率选择表面在无线通信中的应用频率选择表面(Frequency Selective Surface,FSS)是一种由导电和非导电材料组成的平面结构,通过布置不同形状和分布的小结构单元来实现对电磁波的频率选择或滤波。
FSS具有轻薄、低成本、方便制备等优点,已经广泛应用于无线通信系统中。
一、FSS的基本结构和原理FSS的基本单元是一些电性能良好的片状元器件,由互相平行和等间隔排列而成。
这些单元被各自固定在一种介质材料的表面上,形成一个平面结构。
这个平面上的单元由电导材料或其他具有介电性的材料组成,可以通过改变单元的形状和分布,调节电磁波的穿透性能,选择特定的频率。
FSS的原理是基于一系列小电偶极子与辐射之间的相互作用来实现的。
当电波穿过FSS时,部分电波穿过FSS的通道,部分被反射,部分被吸收。
反射和吸收的电波量与FSS单元的大小、形状、距离和流动方向等因素有关。
通过改变这些因素的不同组合,FSS可以实现对不同频率电磁波的选择,并产生频率选择的效应。
二、FSS在无线通信中的应用1.微波通信FSS在微波通信系统中,可以作为一个低成本、高效率的无源光学元件来调节电磁波信号的衰减,延长电磁波信号的传输距离。
另外,FSS还可以作为微波天线的附属元器件,用于优化微波天线的性能。
例如,在机载雷达系统和微波无线电链路等应用中,FSS都具有重要的传输和接收功能。
2.毫米波通信毫米波通信是目前无线通信领域的一个热门话题。
毫米波通信是指在30-300GHz频段内实现宽带无线通信。
由于毫米波频段的传输距离相对较短,适合在狭小的空间内或近距离通信。
FSS在毫米波通信中可以用作频率选择器,用于对不同频率的毫米波进行选择和滤波,优化毫米波通信的传输质量。
3.防御领域在防御领域,FSS可以用作防御性屏蔽罩,以保护关键设备不受电磁干扰和电磁泄漏的影响。
FSS通过改变材料和单元的组合方式和布局,实现对不同频率电磁波的遮蔽和绕射,减小电磁波泄漏的危险。

频率选择表面HFSS报告记录————————————————————————————————作者:————————————————————————————————日期:频率选择表面5.3.1 设计背景频率选择表面(Frequency Selective Surface,FSS)是一种二维周期性结构,可以有效地控制电磁波的反射与传输。
目前FSS的应用十分广泛,可用于反射面天线的负反射器以实现频率复用,提高天线的利用率;也可以用于波极化器、分波数仪和激光器的“腔体镜”,以提高激光器的泵浦功率;还可以用于隐身技术,应用设计的雷达天线罩能够有效地降低雷达系统的雷达散射界面。
5.3.2 设计原理FSS是一种而为周期排列的阵列结构,本身不能吸收能量,但是却能起到滤波的作用。
通常有两种形式,以后总是贴片型,是在介质衬底层上周期性地印上规则的导体贴片单元组成金属阵列;另一种是孔径型,是在很大的金属屏上周期性开孔的周期孔径结构。
这两种结构都可以实现对电磁场的频率选择作用和极化选择作用,对于谐振情况下的入射电磁波,这两种阵列分别表现出全反射(单元为导体贴片)、全透射(单元为缝隙、孔径),它们也被分别称为带阻型FSS和带通型FSS。
频率选择表面的频率选择特性主要取决于写真单元的形式、单元的排布方式以及周围戒指的电性能。
FSS的基本结构如图5-3-1所示,上下层为介质层,中间层为金属层,金属层也可以位于介质层的上下面上。
1.基本的偶极子或缝隙形式的频率选择表面FSS的两类基本形式是导线阵列和缝隙阵列,如图5-3-2所示。
介质基PECε1ε2 μ2图5-3-1 FSS的如图5-3-2(a )所示的谐振偶极子的阵列作为带阻滤波器,不能通行偶极子谐振频率的波,但可以通行高于和低于谐振频率的波。
与之互补的在理想导电片上的缝隙阵列,如图5-3-2(b )所示,用作带通滤波器,可通行等于缝隙谐振频率的波,但拒绝较高和较低频率的波。

频率选择表面的谱域计算及其在WLAN中的应用的
开题报告
本文开题报告的主要内容是关于频率选择表面(FSS)的谱域计算及其在无线局域网络(WLAN)中的应用。
在现代通信系统中,频率选择表面是一种用于实现频率选择和信号
隔离的新型材料。
它由一些具有特殊几何形状的金属结构组成,可以通
过调整这些结构的形状和大小来选择特定的频率带。
本文旨在对FSS的谱域计算方法进行研究,以便更好地理解FSS在WLAN中的应用。
具体来说,本文将从以下两个方面进行研究:
1. FSS的谱域计算方法学习:
本文将介绍几种常用的FSS谱域计算方法,如逆傅里叶变换(IFT)、离散傅里叶变换(DFT)等。
同时,将详细介绍如何用MATLAB编写程序来实现这些计算方法。
2. FSS在WLAN中的应用研究:
本文将研究FSS在WLAN中的应用,主要是在抑制木质材料引起的
信号衰减和提高室内覆盖范围方面的应用。
本文将通过模拟和实验来验
证FSS在WLAN中的应用效果,并进行定量评估。
综上所述,本文将对FSS的谱域计算方法和在WLAN中的应用进行
深入研究,为FSS技术的发展和应用提供有力的理论和实验基础。

频率选择表面的研究起始于上世纪60年代,国内外大批学者均为之投入了大量精力进行广泛深入的工作,提出了各种不同的数学分析与计算方法,如交分法,等效电路法,模式匹配法,谱方法等,这些计算方法主要可分为两大类,即标量分析方法与矢量分析方法。
前者包括变分法,等效电路法等,其仅可通过计算获得关于反射透射系数的幅度信息,通用性差,但计算量小,耗时短;后者包括模式匹配法,谱方法等,其通过计算不仅可获得反射透射系数的幅度信息,还可以获得相关的相位与极化信息,通用性强,但计算量大且耗时长。
值得一提的是,国内研究目前普遍采用模式匹配法进行计算分析,该方法不仅适用于求解任意单元形 状及排列方式的无限大平面FSS 结构,还可应用于多层的FSS 以及均匀层状衬底等组合结构。
但这种方法 依然存在不足,即处理复杂多层FSS 时计算量非常大,而且在数值求解过程中,选择适合复杂单元形状的 基函数非常困难,因而难以保证解的收敛速度,降低了有效性。
与一般模式匹配法相比,谱方法原理上也能分析任意单元形状的FSS 结构,在求解无限大FSS 问题时 与模式匹配法相当,该方法在求解过程中要求选取合适的基函数来保证收敛性,但可直接用于求解有耗FSS 的散射问题,与迭代技术相结合可以求解有限尺寸的FSS 散射问题。
并且谱方法利用了场的周期性,注意 电流分布的周期性特征,所以求解模型简单,计算量小,是一种很好的方法。
谱展开法在周期性结构的分析中,谱展开法是一种重要的分析方法。
Floquet 定理;一维周期结构如图2.5所示。
设入射平面波z TM()0j wt z E E e ϕ-=则空间沿x 方向相距为m 个周期的两点之间场为cos ,(,,)x jm D x x mD y w x y w e βθ-ψ(+,) =ψ式中ψ为电磁场的某一分量。
m 为一整数,β为传播常数,x D 为沿x 方向的周期长度,θ为入射角,上式即是Floquet 定理。
如果这个周期结构的单元是偶极子等贴片型类型,则入射场在单元上将感应出电压,并产生电流,如果我们将其中一个单元的电流作为基准单元电流(表示为0I ),则距它m 个周期的单元电流表示为m I 。

频率选择表面设计原理频率选择表面(Frequency Selective Surface,FSS)是一种具有特定频率选择性的电磁波滤波器,通常被应用于天线、雷达等领域。
频率选择表面的设计原理是非常复杂的,下面我们将逐步详细介绍。
一、频率选择表面的基本原理频率选择表面通常由单元结构重复排列组成,其中每个单元结构都是由金属贴片和介质板组成。
金属贴片的形状及大小、介质板的介电常数等参数决定了频率选择表面的频率特性。
当电磁波传播到频率选择表面上时,会被金属贴片接收、反射、透过或吸收。
通过设置金属贴片的形状及大小,可以控制电磁波的反射和透过,从而实现特定频段的电磁波滤波。
二、频率选择表面的设计步骤1. 确定使用频段在设计频率选择表面之前,需要明确所要使用的频段。
根据频段的不同,需要调整金属贴片的大小、形状、分布方式以及介质板的材料及结构等参数。
2. 选择金属贴片形状不同形状的金属贴片对电磁波的反射和透过具有不同的影响。
在选择金属贴片形状时,需要考虑其反射和透过的频率特性,并确定最佳的形状。
3. 优化金属贴片大小和间距金属贴片的大小和间距也对频率选择表面的频率特性有重要的影响。
通过适当地调整金属贴片大小和间距,可以使频率选择表面在目标频段内具有更优异的性能。
4. 选择介质板材料介质板材料的介电常数对频率选择表面的频率特性也有很大的影响。
需要根据所选频段的介电常数,选择合适的介质板材料。
5. 确定金属贴片的分布方式金属贴片的分布方式是影响频率选择表面性能的另一个因素。
在设计过程中,需要综合考虑金属贴片的形状、大小、间距和介质板材料等因素,确定合适的金属贴片分布方式。
三、应用前景频率选择表面作为一种有效的电磁波滤波器,已经在天线、雷达等领域得到广泛的应用。
在未来,随着通信、雷达等技术的不断发展,频率选择表面的应用前景也将不断拓展。
总之,频率选择表面的设计原理是非常复杂的,需要考虑各种参数的综合影响。
只有深入研究其设计原理,才能够更好地应用于实际场景中,为人们的生活和工作带来更多便利。

带阻频率选择表面的设计详细教程
带阻频率选择表面的设计详细教程
1 引言
频率选择表面(FSS)是二维周期阵列结构,它由周期性排列的金属贴片单元或在金属屏上周期性排列的孔径单元构成。
这种表面可以在单元谐振频率附近呈现全反射(贴片型)或全传输特性(孔径型),分别称为带阻或带通FSS。
实际的带阻段是由一层或多层被介质层分开的FSS贴片层组成。
为了FSS的频率响应相对于入射角和极化的稳定性,金属贴片层通常镶嵌在多层介质层里。
另外,两层或多层FSS 贴片层背靠背叠加在一起可以产生很好的通带特性(平坦的通带,陡降的边带)。
2 带阻频率选择表面的设计
通常的带阻滤波器是由两层FSS金属层和中间的介质层组成。
中间的介质片决定了传输曲线通带的平坦性,FSS金属层决定了传输曲线的带宽和谐振频率。
介质片的厚度和介电常数非常重要。
介质片的厚度典型的被取在0.5,是阻带中心的波长。
两个FSS层之间的介质层提高了带阻滤波器相对于入射角的稳定性。
尽管从稳定性的角度看,介电系数的值越高越好,但是高的值也引入了高的传输损耗。
这样,根据设计需要,必须对介电系数的取值做综合的考虑。
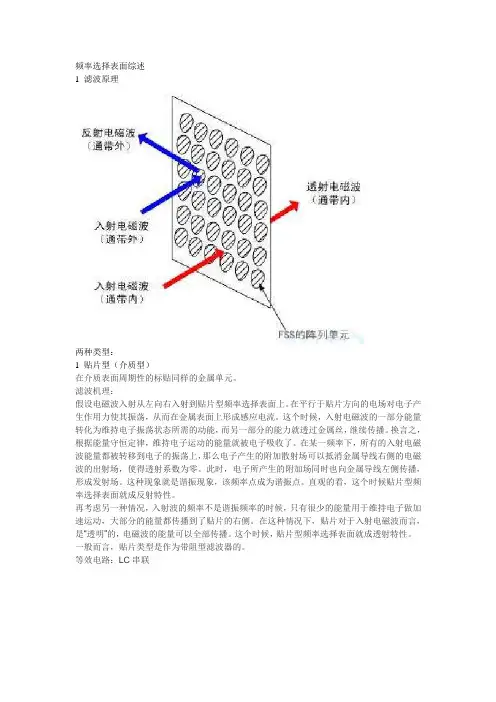
频率选择表面综述1 滤波原理两种类型:1 贴片型(介质型)在介质表面周期性的标贴同样的金属单元。
滤波机理:假设电磁波入射从左向右入射到贴片型频率选择表面上。
在平行于贴片方向的电场对电子产生作用力使其振荡,从而在金属表面上形成感应电流。
这个时候,入射电磁波的一部分能量转化为维持电子振荡状态所需的动能,而另一部分的能力就透过金属丝,继续传播。
换言之,根据能量守恒定律,维持电子运动的能量就被电子吸收了。
在某一频率下,所有的入射电磁波能量都被转移到电子的振荡上,那么电子产生的附加散射场可以抵消金属导线右侧的电磁波的出射场,使得透射系数为零。
此时,电子所产生的附加场同时也向金属导线左侧传播,形成发射场。
这种现象就是谐振现象,该频率点成为谐振点。
直观的看,这个时候贴片型频率选择表面就成反射特性。
再考虑另一种情况,入射波的频率不是谐振频率的时候,只有很少的能量用于维持电子做加速运动,大部分的能量都传播到了贴片的右侧。
在这种情况下,贴片对于入射电磁波而言,是“透明”的,电磁波的能量可以全部传播。
这个时候,贴片型频率选择表面就成透射特性。
一般而言,贴片类型是作为带阻型滤波器的。
等效电路:LC串联2 开槽型(波导型)在金属板上周期性的开一些金属单元的槽孔。
滤波机理:当低频电磁波照射开槽型频率选择表面时,将激发大范围的电子移动,使得电子吸收大部分能量,且沿缝隙的感应电流很小,导致透射系数比较小。
随着入射波频率的不断升高,这种电子移动的范围将逐渐较小,沿缝隙流动的电流在不断增加,从而透射系数会得到改善。
当入射电磁波的频率达到一定值时,槽两侧的电子刚好在入射波电场矢量的驱动下来回移动,在缝隙周围形成较大的感应电流。
由于电子吸收大量入射波的能量,同时也在向外辐射能量。
运动的电子透过偶极子槽的缝隙向透射方向辐射电场,此时的偶极子槽阵列反射系数低,透射系数高。
当入射波频率继续升高时,将导致电子的运动范围减小,在缝隙周围的电流将分成若干段,电子透过槽缝隙辐射出去的电磁波减小,因此,透射系数降低。

带阻频率选择表面的设计详细教程
1 引言
频率选择表面(FSS)是二维周期阵列结构,它由周期性排列的金属贴片单元或在金属屏上周期性排列的孔径单元构成。
这种表面可以在单元谐振频率附近呈现全反射(贴片型)或全传输特性(孔径型),分别称为带阻或带通FSS。
实际的带阻段是由一层或多层被介质层分开的FSS贴片层组成。
为了FSS的频率响应相对于入射角和极化的稳定性,金属贴片层通常镶嵌在多层介质层里。
另外,两层或多层FSS贴片层背靠背叠加在一起可以产生很好的通带特性(平坦的通带,陡降的边带)。
2 带阻频率选择表面的设计
通常的带阻滤波器是由两层FSS金属层和中间的介质层组成。
中间的介质片决定了传输曲线通带的平坦性,FSS金属层决定了传输曲线的带宽和谐振频率。
介质片的厚度和介电常数非常重要。
介质片的厚度典型的被取在0.5,是阻带中心的波长。
两个FSS层之间的介质层提高了带阻滤波器相对于入射角的稳定性。
尽管从稳定性的角度看,介电系数的值越高越好,但是高的值也引入了高的传输损耗。
这样,根据设计需要,必须对介电系数的取值做综合的考虑。

频率选择变面的边界条件的反射率一、概述1. 频率选择表面是一种特殊的表面结构,能够对特定频率的电磁波进行选择性反射或透射。
2. 在设计频率选择表面时,其边界条件的反射率是一个非常重要的参数。
3. 本文将从数学模型和实际应用两个方面探讨频率选择变面的边界条件的反射率。
二、数学模型4. 频率选择变面可以用Maxwell方程组描述,其中包括电磁波在频率选择表面上的传播和反射。
5. 在边界条件的处理上,常用的方法包括矢量电磁场理论、电偶极子理论等。
6. 通过建立数学模型,可以分析出频率选择表面在不同频率下的反射率特性。
三、频率选择表面的边界条件7. 频率选择表面通常包括导电片和介质层,其边界条件对反射率有重要影响。
8. 不同形式的频率选择表面,如金属贴片阵列、绝缘贴片阵列等,其边界条件的处理方法有所不同。
9. 针对不同形式的频率选择表面,需要分别进行边界条件的求解和反射率的计算。
四、频率选择表面的反射率计算10. 在实际应用中,需要根据频率选择表面的结构和工作频率,计算其边界条件下的反射率。
11. 通过数值计算或仿真模拟,可以得到频率选择表面在不同频率下的反射率曲线。
12. 反射率的计算结果可以用于指导频率选择表面的设计和优化,以满足特定的应用需求。
五、频率选择表面在通信和雷达中的应用13. 频率选择表面在通信和雷达系统中有着广泛的应用,如天线、隐身技术等。
14. 通过调整频率选择表面的反射率特性,可以实现对电磁波的精确控制和调制。
15. 在通信和雷达系统中,频率选择表面的边界条件的处理和反射率的设计是十分关键的。
六、结论16. 频率选择变面的边界条件的反射率是影响其性能的重要参数,需要通过数学建模和实际计算来确定。
17. 通过合理设计频率选择表面的边界条件和反射率特性,可以实现对电磁波的有效控制和利用。
18. 频率选择表面在通信和雷达等领域的应用前景广阔,对其反射率特性的研究具有重要意义。
七、频率选择表面的设计与优化1. 频率选择表面的设计与优化是一个复杂而重要的工作。
三维频率选择表面一、引言频率选择表面(FSS)是一种重要的电磁特性材料,能够实现特定频率的电磁波的传输和反射。
传统的二维频率选择表面已经得到了广泛的应用,但是随着科技的发展,人们对频率选择表面的性能和应用领域提出了更高的要求。
因此,三维频率选择表面应运而生,具有更高的灵活性和更广泛的应用前景。
二、三维频率选择表面的基本原理频率选择表面的工作原理主要是利用金属或半导体的薄膜或贴片在特定频率下呈现出不同的电导性和介电常数,从而实现对电磁波的传输和反射。
三维频率选择表面则是将传统的二维结构扩展到三维空间,通过设计不同形状和大小的单元结构,实现对不同方向和角度的电磁波的传输和反射。
三、三维频率选择表面的研究现状目前,国内外对三维频率选择表面的研究主要集中在设计方法、制备工艺和性能优化等方面。
一些最新的研究成果已经展示了三维频率选择表面的巨大潜力。
例如,一种基于FDTD算法的三维频率选择表面设计方法,可以实现精确的电磁波控制和优化;一种基于纳米压印技术的三维频率选择表面制备工艺,可以获得高精度、高稳定性的结构;一种具有高透射率和宽频带的三维频率选择表面,可以实现高效的电磁波传输和反射。
四、三维频率选择表面的应用领域三维频率选择表面具有广泛的应用领域,包括军事、通信和雷达系统等。
在军事领域,三维频率选择表面可以实现雷达隐身、红外隐身和电磁防护等功能;在通信领域,三维频率选择表面可以用于天线设计、电磁屏蔽和电磁兼容等方面;在雷达系统领域,三维频率选择表面可以用于雷达信号处理、目标识别和跟踪等方面。
五、三维频率选择面的挑战与解决方案尽管三维频率选择表面具有广泛的应用前景,但也面临着一些挑战,如制造工艺、性能提升和应用拓展等。
针对这些问题,可以采取一些解决方案,如采用先进的纳米压印技术实现高精度结构制备;通过优化设计方法和制备工艺提高三维频率选择表面的性能;拓展三维频率选择表面的应用领域,如生物医学、环境监测等领域。
文章编号:100526122(2006)0120048204含各向异性介质衬底频率选择表面的直线法分析3林宝勤,徐利军,袁乃昌(国防科技大学电子科学与工程学院微波技术中心,长沙410073)摘 要: 运用直线法对一以单轴各向异性介质层为衬底的频率选择表面(FSS)进行了分析,考虑到介质层的各向异性,文中对直线法的常用方式作出了一定的修改,并详细介绍了整个方法实现过程。
最后,对几套不同介电参数的FSS进行了计算,考虑了介质衬底的各向异性对FSS电磁特性的影响。
关键词: 频率选择表面,介质各向异性,直线法Analysis of Frequency Selecti ve Surfaces withUn i a xi a l An isotropi c SubstrateL I N Bao2q i n,XU L i2jun,Y UAN Na i2chang(Institute of Electronic Science and Engineering,NUD T,Changshai410073,China)Abstract: The scattering of electr omagnetic waves fr om Frequency Selective Surfaces(FSS)with uniaxial anis otr op ic substrates is investigated by means of the M ethod of L ines.The Method of L ines is modified because of the dielectric anis ot2 r opy and the p r ocess of the method is p resented in detailed.Finally,Some FSS with different dielectric para meters are com2 puted,and the influence of dielectric anis otr opy on the electr omagnetic characteristics of FSS is considered.Key words: Frequency selective surfaces(FSS),D ielectric anis otr opy,Method of line引 言频率选择表面(FSS)是一种周期性的平面结构,对不同频段的入射电波具有有选择性的反射或透射特性,因而在卫星、雷达以及现代通信系统中得到了广泛应用[1~4]。
频率选择表面滤波器设计优化在电子学领域中,频率选择表面滤波器是一个重要的器件,它可以帮助我们过滤掉不需要的频段,将信号保留在我们想要的频域中。
它的广泛应用范围包括无线通信、卫星通信和雷达等领域。
今天,我将会和大家分享一些频率选择表面滤波器设计优化的方法。
首先,让我们回忆一下频率选择表面滤波器的基本原理。
它是由介电材料层和金属导电层交替组成的结构。
而滤波器的性能取决于介电常数、尺寸和层数等参数。
在选取材料方面,我们应该选择具备高介电常数和低损耗的材料,这样可以帮助我们提高滤波器的性能。
在此基础上,我们通过优化尺寸和层数等参数,以达到更好的滤波效果。
接着,让我们来谈谈如何进行优化设计。
一般来说,优化设计需遵循以下步骤:第一步,制定设计目标。
我们需要明确具体的设计需求,如中心频率、带宽和插入损耗等。
第二步,确定初始结构参数。
我们需要在制定好设计目标后,初步确定滤波器的结构参数,如层数、介质种类、缝隙宽度等等。
第三步,选择合适的优化算法。
现在常用的优化算法包括遗传算法、粒子群算法、模拟退火算法和蚁群算法等。
不同的算法适用于不同的问题,我们需要根据实际情况选择合适的算法。
第四步,优化计算模型。
为了方便计算,我们需要利用电磁场仿真软件进行滤波器的仿真计算。
而在利用仿真进行优化时,我们需要根据实际情况制定仿真模型,学习仿真技巧和方法,以确保仿真计算的准确性和可靠性。
第五步,进行优化计算。
在确定好优化算法和计算模型后,我们可以进行优化计算了。
在进行计算时,需要注意求解的精度、迭代次数和收敛条件等。
第六步,优化结果分析。
在计算结束后,我们需要对结果进行分析和评价。
分析结果的优劣,判断是否达到设计目标,为下一步的设计工作提供更好的方向和条件。
除了上述基本步骤外,我们在进行频率选择表面滤波器设计与优化的过程中,还需要注意以下几个基本问题:一是优化目标的确定。
因为不同的设计目标,需要寻找不同的优化算法。
比如,我们优化插入损耗和中心频率时,可以选用遗传算法或者粒子群算法。
硕士学位论文基于等效电路的频率选择表面分析与设计摘要频率选择表面(FSS)单元结构的传统设计方法,更多依赖设计者的经验和多次全波仿真的尝试,而本文将根据FSS的等效电路,结合贴片电感、贴片电容、叉指电容、弯折线电感等构建周期单元,以探索FSS的高效设计方法,具体内容如下1.基于集总电感电容的FSS设计及研制基于单双频FSS的等效电路,利用集总贴片电感、电容构建FSS单元结构,完成了谐振频率为4.37GHz的单频FSS和谐振频率为2.5GHz、5.25GHz的双频FSS设计、加工和测试,两种FSS的单元尺寸分别达到1/14波长和1/12波长,并具备良好的极化和倾斜角度稳定性。
2.基于准集总电感电容的FSS设计及研制为解决贴片电感、电容加载FSS需要焊接、成本高等问题,基于单双频FSS 等效电路,利用叉指电容、弯折线电感构建全平面的FSS谐振单元,完成了谐振频率为2.6GHz和5GHz的双频FSS设计、加工和测试,测试结果与仿真结果较为一致。
3.基于等效电路的FSS吸波体设计研究研究了FSS吸波体的工作原理和等效电路,利用集总贴片电阻,开展了8-20GHz波段吸波体设计研究,获得了比较好的带宽和吸波性能,其单元厚度为1/12波长,8-20GHz波段反射系数小于-10dB。
关键词:频率选择表面、等效电路、电感、电容、吸波体IAbstract 硕士学位论文II AbstractThe traditional design methods of Frequency Selective Surface (FSS) depend more on the designers’ experience and their multiple attempts of full wave simulation. According to the equivalent circuit of FSS, this article will explore an effective design method of FSS, combining lumped inductors, lumped capacitors, interdigital capacitors, meander line inductors and other construction cycle units. Specific content is as follows.1. FSS design based on lumped inductance and capacitanceBased on the equivalent circuit of single-frequency and double-frequency FSS, and the use of lumped inductance and capacitance to build FSS unit, this author completes the design, processing and test of the single-frequency FSS with resonant frequency of 4.37 GHz and the double-frequency FSS with resonant frequencies of 2.5 GHz and 5.25 GHz. The cell sizes of these two kinds of FSS respectively are 1/14 wavelength and 1/12 wavelength, with good polarization and tilt angle stability.2. FSS design based on quasi-lumped inductance and capacitanceWhen lumped inductance and capacitance loads FSS, it needs welding and is of high cost. In order to solve this problem, this author bases the design on the equivalent circuit of single-frequency and double-frequency FSS, uses the interdigital capacitor and meander line inductor to build a full-plane FSS resonant unit, and completes the design, processing and test of double-frequency FSS with resonant frequencies of 2.6GHz and 5GHz. The test results are consistent with the simulation results.3. FSS absorber design research based on equivalent circuitThe working principle and equivalent circuit of FSS absorber are studied. The lumped patch resistance is used to do design research on absorber of 8-20GHz waveband, and good bandwidth and absorption property are obtained. The unit size is 1/12 wavelength and the reflection coefficient of 8-20GHz waveband is less than -10db.Key word: frequency selective surface, equivalent circuit, inductance, capacitance, absorber硕士学位论文基于等效电路的频率选择表面分析与设计目录摘要 (I)Abstract (II)目录 (III)1绪论 (1)1.1研究背景及意义 (1)1.2频率选择表面简介 (2)1.2.1频率选择表面概述 (2)1.2.2频率选择表面的主要研究方法 (3)1.3本文研究工作 (5)2基于集总电感电容的FSS设计及研制 (6)2.1 等效电路阐述 (6)2.1.1 单频透射型FSS及等效电路分析 (6)2.1.2单频反射型FSS及等效电路分析 (6)2.2 基于等效电路的集总元件小型化单频FSS仿真设计 (7)2.2.1结构设计 (7)2.2.2 仿真及性能分析 (8)2.2.3 小结 (10)2.3基于等效电路的集总电感电容加载双频FSS设计与制备 (10)2.3.1 基于等效电路的结构设计 (10)2.3.2仿真及性能分析 (12)2.3.3样品加工和测试 (15)2.4本章小结 (16)3基于准集总电感电容的FSS设计及研制 (17)3.1引言 (17)3.2基于弯折线和贴片电容双频FSS设计与仿真 (17)3.2.1 改进结构一 (17)3.2.2仿真及性能分析 (18)3.2.3改进结构二 (20)3.2.4仿真及性能分析 (21)3.3基于等效电路的叉指电容和弯折线电感双频FSS设计与制备 (22)III目录硕士学位论文IV 3.3.1结构设计 (22)3.3.2仿真及性能分析 (23)3.3.3样品加工与测试 (25)3.4 本章小结 (28)4基于等效电路的FSS吸波体设计研究 (29)4.1 吸波材料简介 (29)4.2结构设计 (30)4.3等效电路分析 (30)4.4仿真及性能分析 (31)4.5本章小结 (35)5总结与展望 (36)致谢 (37)参考文献 (38)附录 (42)硕士学位论文 基于等效电路的频率选择表面分析与设计 11绪论1.1研究背景及意义频率选择表面(Frequency Selective Surface ,简称FSS )[1]是一种由贴片金属单元[2]或金属开槽单元构成的起空间滤波作用的二维周期性阵列结构。
频率选择表面的制备与应用研究频率选择表面(FSS)作为一种新兴的微波器件,具有广泛的应用前景。
其核心技术是在介电基板的表面上通过打印等方式制作出周期性电磁结构,以达到对微波信号的选择性反射或透射作用。
随着科技的不断发展,FSS在雷达、天线、无线通信等领域得到了广泛应用,是目前研究的热点之一。
一、FSS的制备方法FSS的制备方法主要有三种:压致法、光固化法和微细加工法。
1. 压致法:将聚合物基质加热至玻璃化转变温度以上,在压力作用下使介电芯片表面的FSS压成周期性结构,在热处理过程中使其固化后即可得到FSS。
压致法制备FSS具有制备简单、成本低、适用范围广等优点,但是FSS的周期和结构参数难以控制,品质不稳定。
2. 光固化法:利用紫外线将定位的光敏树脂加热凝固,然后在树脂中加入铜结构的模板,再照光,最后将树脂进行清洗,在铜结构内填充金属,形成一层铜膜,即为FSS。
光固化法制备FSS具有制备精度高、过程可控等优点,但是需要使用高精度的曝光和刻蚀设备,成本较高。
3. 微细加工法:将FSS图案加工至铜箔中,然后将铜箔刻蚀后,采用电解金属沉积技术制备出FSS。
微细加工法制备FSS具有周期约束性、FSS金属膜阻抗适应性好、制备精度高等优点,但是加工难度大、制备周期长、成本高。
二、FSS的应用研究1.雷达技术雷达技术在航空、航海、军事等领域有着重要的应用。
FSS在雷达技术中可以用来设计一些用于欺骗和误导敌方雷达系统的复杂结构。
通过设计FSS的反射、透射系数,可以使雷达无法探测目标,产生干扰信号,从而实现战争中的优势。
2. 天线技术FSS在天线技术中也是有着广泛的应用。
在卫星通信中,FSS可以用于设计某些方向性天线,控制信号的传播方向,具有指向性和频率选择性。
在车载天线等应用中,FSS可以用于解决可能出现的多重信号干扰问题,加强信号的传输效果。
3. 无线通信技术FSS在无线通信技术中的应用也是非常广泛的。
在5G通信中,FSS可以用于设计某些用于增强信号强度和波束成形的结构。
FSS--相关知识整理
一、基本概念
1、频率选择表面(Frequency Selective Surface ,FSS) 是一种二维周期阵列结构,就其本质而言是一个空间滤波器,与电磁波相互作用表现出明显的带通或带阻的滤波特性。
FSS 具有特定的频率选择作用而被广泛地应用于微波、红外至可见光波段。
2、分类
频率选择表面有两种:贴片类型也叫介质类型,开槽类型也叫波导类型。
贴片类型是在介质表面周期性的标贴同样的金属单元,一般而言是作为带阻型滤波器的;低频透射,高频反射;
开槽类型是在金属板上周期性的开一些金属单元的槽孔,从频率特性相应上看是带通型频率选择表面;低频反射,高频透射。
3、频率选择表面的应用
雷达罩:通过安装频率选择表面减少雷达散射截面积。
卡塞哥伦天线副反射面:实现波束的复用与分离。
准光滤波器:实现波束的复用与分离。
吸波材料:基于高损耗的介质,可以实现大带宽的吸波材料。
极化扭转:折线形的频率选择表面是一个线极化变成圆极化的极化扭转器。
天线主面:降低带外的噪声。
4、滤波机理
图1 频率选择表面的滤波机理
频率选择表面和一般意义上的通过电容、电感组成的滤波器在目的上是一致。
而滤波机理和有很大的区别(图1)。
最大的区别是,一般的滤波器作用的对象是电路中的电流,而且一般滤波器我们主要关心通带的波形是不是有畸变,而对于阻带就就不必关心了。
而频率选择表面是对于场的滤波器,不论是透射波还是反射波都是十分重要,不仅仅要关注其幅度、相位的变化,还要关心交叉极化和热损耗等。
A、贴片类型:在介质表面周期性的标贴同样的金属单元。
图2 贴片类型频率选择表面的等效电路
滤波机理:
假设电磁波入射从左向右入射到贴片型频率选择表面上。
在平行于贴片方向的电场对电子产生作用力使其振荡,从而在金属表面上形成感应电流。
这个时候,入射电磁波的一部分能量转化为维持电子振荡状态所需的动能,而另一部分的能力就透过金属丝,继续传播。
换言之,根据能量守恒定律,维持电子运动的能量就被电子吸收了。
在某一频率下,所有的入射电磁波能量都被转移到电子的振荡上,那么电子产生的附加散射场可以抵消金属导线右侧的电磁波的出射场,使得透射系数为零。
此时,电子所产生的附加场同时也向金属导线左侧传播,形成发射场。
这种现象就是谐振现象,该频率点成为谐振点。
直观的看,这个时候贴片型频率选择表面就成反射特性。
再考虑另一种情况,入射波的频率不是谐振频率的时候,只有很少的能量用于维持电子做加速运动,大部分的能量都传播到了贴片的右侧。
在这种情况下,贴片对于入射电磁波而言,是“透明”的,电磁波的能量可以全部传播。
这个时候,贴片型频率选择表面就成透射特性。
一般而言,贴片类型是作为带阻型滤波器的。
等效电路:LC串联
B、贴片类型:在金属板上周期性的开一些金属单元的槽孔。
滤波机理:
当低频电磁波照射开槽型频率选择表面时,将激发大范围的电子移动,使得电子吸收大部分能量,且沿缝隙的感应电流很小,导致透射系数比较小。
随着入射波频率的不断升高,这种电子移动的范围将逐渐较小,沿缝隙流动的电流在不断增加,从而透射系数会得到改善。
当入射电磁波的频率达到一定值时,槽两侧的电子刚好在入射波电场矢量的驱动下来回移动,在缝隙周围形成较大的感应电流。
由于电子吸收大量入射波的能量,同时也在向外辐射能量。
运动的电子透过偶极子槽的缝隙向透射方向辐射电场,此时的偶极子槽阵列反射系数低,透射系数高。
当入射波频率继续升高时,将导致电子的运动范围减小,在缝隙周围的电流将分成若干段,电子透过槽缝隙辐射出去的电磁波减小,因此,透射系数降低。
而对于在远离缝隙的金属板上所产生的感应电流则向反射方向辐射电磁场,并且由于高频电磁波的电场变化周期的限制了电子的运动,辐射能量有限。
因此,当高频电磁波入射时,透射系数减小,反射系数增大。
图5-1 贴片类型频率选择表面的等效电路
图3 贴片类型频率选择表面的等效电路
从频率特性相应上看,开槽型频率选择表面是带通型频率选择表面。
等效电路:LC并联
C、贴片类型和开槽类型频率选择表面的关系:
在不考虑介质的情况下,他们是互补的,可以看出开槽类型的频率选择表面与贴片型频率选择表面相比,开槽型频率选择表面具有相反的频率响应特性。
在低于谐振频率时,开槽类型的呈现感性电路特性;在高于谐振频率是呈现容性电路特性。
从等效电路方法的角度来看,开槽型频率选择表面可以表述为电容电感并联的等效电路。
在入射电磁波频率为谐振频率时,开槽型频率选择表面对谐振频率的电磁波是“透明”的。
而贴片类型的频率选择表面恰恰相反。
二、存在的问题,设计的思路
描述FSS 频率响应特性的主要指标有中心频率、中心频率处的透过率、传输带宽等。
这些特性主要取决于FSS 谐振单元的形式,单元的排布方式以及周围介质的电性能。
影响这些特性的因素很多,其中入射波的极化方式与入射角度是两个重要的影响因素。
1、在FSS 的实际工程应用中,很多情况下入射波的极化方式是未知的,并且入射角度范围大,此时要采用一种对不同入射角度和极化方式性能都稳定的FSS 结构,即兼具极化和角度稳定性的FSS。
2、传统正方形栅格排布的十字单元FSS 具有结构的对称性,在正入射时具有极化稳定性,但是当入射电磁波的入射角度增大时, 谐振频率随极化方式的改变有很大的漂移,这极大地降低了FSS 的性能;另一方面十字单元和一般普通单元一样随入射角度的变化,中心频率不具备角度稳定性,漂移量很大。
这是FSS 实现工程应用急需解决的问题。
同时对于FSS 极化稳定性的问题,正入射时可以选取对称单元实现极化稳定性,但是工程应用中往往涉及到大的入射角度,此时仅仅依靠单元的对称性已经不能实现结构的极化稳定性。
3、侯新宇等通过优选图形单元2Y孔单元的方法来实现FSS 对入射角度的稳定性,但Y 形单元极化稳定性不好。
4、Munk 等则是采用加载电介质的方式改善大角度入射时FSS 的传输特性,但加载电介质又往往会增加传输损耗。
三、分析的方法
沿一维或二维方向周期排列的金属贴片阵列或金属平面上的孔径阵列可实现低通、高通、带通和带阻等不同的滤波器特性, 常被称为频率选择表面(FSS)。
习惯上, 低通和高通的FSS 又分别被称为感性FSS 和容性FSS。
FSS 的应用几乎涉及所有的电磁波谱, 如卫星天线的频率复用、天线罩、电路模拟吸收体以及各种空间滤波器和准光频率器件等。
由于结构复杂、参数众多, FSS 的理论分析和设计非常困难。
近年来已发展的一些数值方法, 如时域有限差分(FDTD )、有限元(FEM ) 以及积分方程( IE) 方法等由于计算内存占用量大、计算量大, 从而导致计算效率很低。
FSS 在入射波作用下所表现出来的物理现象,可以通过传输线理论近似, 因此根据等效电路的原理, 加以不同的极化和角度入射条件, 可将FSS 单元用相
应的电路元件来等效。
从而对FSS 进行快捷的分析。
形状简单的单元(带栅型、网格型、栅环型、方环型等) , 其等效电路及相关的等效参数容易确定,而且分析结果与实际吻合很好[2, 3 ]。
其它几何形状的单元, 则由于等效电路参数不易直接获取而在应用中受到限制[4, 5 ]。