5.1图(经典运筹学)
- 格式:ppt
- 大小:3.22 MB
- 文档页数:43


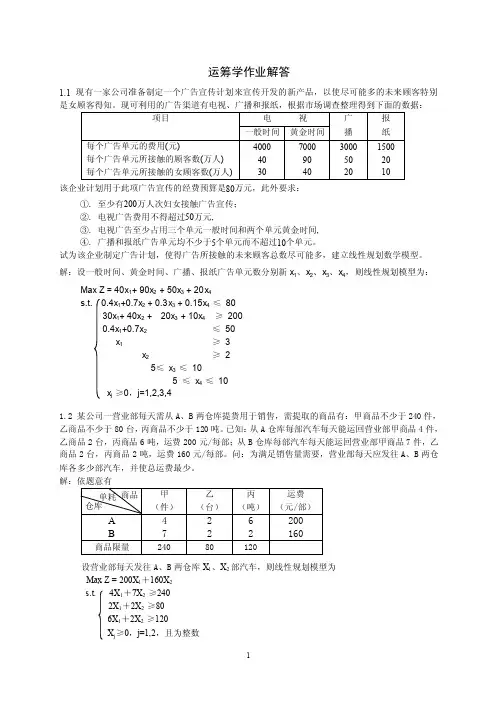
运筹学作业解答1.1 现有一家公司准备制定一个广告宣传计划来宣传开发的新产品,以使尽可能多的未来顾客特别是女顾客得知。
现可利用的广告渠道有电视、广播和报纸,根据市场调查整理得到下面的数据:该企业计划用于此项广告宣传的经费预算是80万元,此外要求:①. 至少有200万人次妇女接触广告宣传;②. 电视广告费用不得超过50万元,③. 电视广告至少占用三个单元一般时间和两个单元黄金时间,④. 广播和报纸广告单元均不少于5个单元而不超过10个单元。
试为该企业制定广告计划,使得广告所接触的未来顾客总数尽可能多,建立线性规划数学模型。
解:设一般时间、黄金时间、广播、报纸广告单元数分别新x1、x2、x3、x4,则线性规划模型为:1.2 某公司一营业部每天需从A、B两仓库提货用于销售,需提取的商品有:甲商品不少于240件,乙商品不少于80台,丙商品不少于120吨。
已知:从A仓库每部汽车每天能运回营业部甲商品4件,乙商品2台,丙商品6吨,运费200元/每部;从B仓库每部汽车每天能运回营业部甲商品7件,乙商品2台,丙商品2吨,运费160元/每部。
问:为满足销售量需要,营业部每天应发往A、B两仓库各多少部汽车,并使总运费最少。
解:依题意有设营业部每天发往A、B两仓库X1、X2部汽车,则线性规划模型为Max Z = 200X1+160X2s.t. 4X1+7X2 ≥2402X1+2X2 ≥806X1+2X2 ≥120X j≥0,j=1,2,且为整数用图解法得最优解为:X* = (10, 30)TZ* = 6800答案:最优解为X*=(15/4 , 3/4 , 0 , 0 )T,Z* =33/41.4 用二阶段法求下列线性规划问题,并用图解法说明二个阶段各步迭代与图解的基本解点的对应关系。
Min Z = 2x1 +4x2s.t.x1 +5x2 ≤ 804x1 +2x2 ≥ 20x1 +x2 = 10x1、x2 ≥ 0答案:最优解为X* = (10,0)T,Z* = 201.5判断下列说法是否正确? 为什么?(1) 在单纯形法迭代中,任何从基变量中替换出来的变量在紧接着的下一次迭代中可能会再进入基变量。


第五章 目标规划§5.1重点、难点提要一、目标规划的基本概念与模型特征 (1)目标规划的基本概念。
当人们在实践中遇到一些矛盾的目标,由于资源稀缺和其它原因,这些目标可能无法同时达到,可以把任何起作用的约束都称为“目标”。
无论它们是否达到,总的目的是要给出一个最优的结果,使之尽可能接近制定的目标。
目标规划是处理多目标的一种重要方法,人们把目标按重要性分成不同的优先等级,并对同一个优先等级中的不同目标赋权,使其在许多领域都有广泛应用。
在目标规划中至少有两个不同的目标;有两类变量:决策变量和偏差变量;两类约束:资源约束(也称硬约束)和目标约束(也称软约束)。
(2)模型特征。
目标规划的一般模型:⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=≥==-+=≤⎪⎭⎫ ⎝⎛+=+-=+-===++--∑∑∑∑.,,2,1;0,;,,2,10,,2,1,,2,1..)(min 1111K k d d n j x K k g d d x c m i b x a t s d d P Z k k j n j k k k j kj i nj j ij Lr K k k rk k rk r ωω 其中r P 为目标优先因子,+-rk rk ωω,为目标权系数,+-k k d d ,为偏差变量。
1)正、负偏差变量,i i d d +-。
正偏差变量i d +表示决策值超过目标值的部分;负偏差变量i d -表示决策值未达到目标值的部分。
因为决策值不可能既超过目标值同时又未达到目标值,所以有0i i d d +-⨯=。
2)硬约束和软约束。
硬约束是指必须严格满足的等式约束和不等式约束;软约束是目标规划特有的。
我们可以把约束右端项看成是要努力追求的目标值,但允许发生正、负偏差,通过在约束中加入正、负偏差变量来表示努力的结果与目标的差距,于是称它们为目标约束。
3)优先因子与权系数。
一个规划问题通常有若干个目标,但决策者在要求达到这些目标时,是有主次或缓急之分的。




