六年级数学几何操作题专项训练
- 格式:doc
- 大小:131.50 KB
- 文档页数:3

苏教版小学六年级数学下册专项练习:几
何题
本文档包含了苏教版小学六年级数学下册的几何题专项练。
几
何是数学的一个重要分支,通过几何题的练,学生可以加深对几何
概念和几何形状的认识,并提高解决几何问题的能力。
请按照以下题目进行练:
1. 计算下列各图形的面积:
- 一个矩形的长为8厘米,宽为3厘米。
请计算该矩形的面积。
- 一个正方形的边长为5厘米。
请计算该正方形的面积。
- 一个三角形的底边长为6厘米,高度为4厘米。
请计算该三
角形的面积。
2. 计算下列各图形的周长:
- 一个矩形的长为10厘米,宽为5厘米。
请计算该矩形的周长。
- 一个正方形的边长为6厘米。
请计算该正方形的周长。
- 一个三角形的三边长度分别为4厘米、5厘米和6厘米。
请计算该三角形的周长。
3. 根据已知条件,判断下列说法的正误:
- 一个四边形的边长都相等,那么它一定是正方形。
【正误】- 如果一个三角形的两边长度相等,那么该三角形一定是等腰三角形。
【正误】
- 如果两条直线反向延长后相交,那么它们一定垂直相交。
【正误】
以上是本文档的部分内容示例,希望对你的学习有所帮助。
祝你顺利完成数学几何题的练习!。

人教版六年级数学下册《图形与几何》专项训练姓名: ___________班级: ___________考号: ___________一、填空题1. 一个等腰三角形的一条边长是, 另一条边长是, 那么这个等腰三角形的周长是(______)。
2. 钟面上, 经过3小时, 时针旋转了(______);经过30分钟, 分针旋转了(______)。
3. 一个梯形的下底是, 如果下底缩短, 那么面积就减少, 并且得到的新图形是一个平行四边形, 原来梯形的面积是(__________)。
4. 如右图, 直角梯形的周长, 它的面积是(________)。
5. 一个长方体正好可以切成4个棱长为的正方体, 原长方体的棱长总和可能是(______), 也可能是(______)。
6.右图是一个圆柱和一个圆锥, 圆柱的底面直径是圆锥的2倍, 它们的高度相等。
一个这样的圆柱可以熔铸成(________)个这样的圆锥。
7.观察下图, 图①和图②中的三角形均为等边三角形, 图①中小三角形的面积是大三角形面积的。
图③中小正方形的面积占大正方形面积的。
8. 小明从一个长方体纸盒上撕下两个相邻的面(展开后如右图), 这个纸盒的底面积是_____平方厘米, 体积是_____立方厘米.9.如下图所示, 一张长方形铁皮, 切割下阴影部分的两个圆和一个长方形刚好能做一个油桶, 这个油桶的容积是(________)。
10. 右图中圆的面积与长方形面积相等。
圆的周长是, 那么阴影部分的周长是(______)。
二、选择题11. 图中正方形的面积()平行四边形的面积。
A. 大于B. 等于C. 小于D. 无法判断12.用10倍的放大镜看40°的角, 看到的角是()A. 40°B. 400°C. 4°13.一个等腰三角形的一个底角是, 它的顶角是()。
A. B. C. D.14.下列四个图形中, 不能通过基本图形平移得到的是()。

六年级上册操作题大全一、圆的相关操作题(5题)题目1:用圆规画一个半径为3厘米的圆,并标记出圆心、半径和直径。
解析:- 操作步骤:- 把圆规的两脚分开,定好两脚之间的距离为3厘米(即半径)。
- 把有针尖的一只脚固定在一点(即圆心)。
- 把装有铅笔尖的一只脚绕圆心旋转一周,就画出一个圆。
- 用字母“O”表示圆心,半径用“r = 3厘米”表示,直径用“d = 6厘米”表示(d = 2r)。
题目2:在一个边长为6厘米的正方形内画一个最大的圆,求这个圆的面积。
解析:- 操作步骤:- 这个圆的直径等于正方形的边长,即d = 6厘米,所以半径r = 3厘米。
- 根据圆的面积公式S=πr²,S = 3.14×3² = 3.14×9 = 28.26(平方厘米)。
题目3:将一个直径为8厘米的圆平均分成4份(用画图表示)。
解析:- 操作步骤:- 先画出直径为8厘米的圆(圆规两脚距离为4厘米画圆)。
- 过圆心画两条互相垂直的直径,这样就把圆平均分成了4份。
题目4:画一个圆,使它的周长是18.84厘米,求这个圆的半径并画出这个圆。
解析:- 操作步骤:- 根据圆的周长公式C = 2πr,已知C = 18.84厘米,18.84=2×3.14×r,解得r = 3厘米。
- 然后用圆规画出半径为3厘米的圆。
题目5:在一个长8厘米、宽5厘米的长方形内画一个最大的半圆,求这个半圆的周长。
解析:- 操作步骤:- 这个半圆的直径应取长方形的长8厘米,半径r = 4厘米。
- 半圆的周长 = 圆周长的一半+直径,即C = 1/2×2×3.14×4+8 = 12.56 + 8 = 20.56(厘米)。
二、分数相关操作题(5题)题目6:把一个长方形平均分成5份,其中的3份用分数表示,并画图。
解析:- 操作步骤:- 画一个长方形。
- 把长方形的长或宽平均分成5等份。
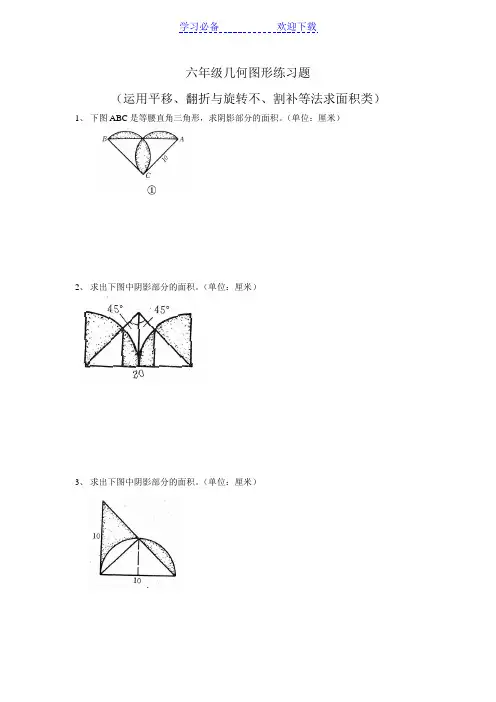
六年级几何图形练习题(运用平移、翻折与旋转不、割补等法求面积类)1、下图ABC是等腰直角三角形,求阴影部分的面积。
(单位:厘米)2、求出下图中阴影部分的面积。
(单位:厘米)3、求出下图中阴影部分的面积。
(单位:厘米)4、求出下图中阴影部分的面积。
(单位:厘米)5、在半径为10厘米,圆心角为90°的扇形中,分别以两条半径的中点E和F为圆心,以扇形半径之半为半径,画两个半圆交于D。
求图中阴影部分的面积(如下图)。
6、求出下图阴影部分的面积。
(单位:厘米)7、求出下图阴影部分的面积。
(单位:厘米)8、下图,直径AB=20厘米,阴影Ⅰ的面积比阴影Ⅱ的面积大7平方厘米,求BC的长。
9、如下图,四个圆的直径均为4厘米,求阴影部分面积。
(单位:厘米)10、下图中各小圆的半径为1,求该图中阴影部分的面积。
11、已知右图中两个正方形的边长分别是3厘米和6厘米,求阴影部分的面积。
12、下图的中的正方形的边长是2厘米,以圆弧为分界线的Ⅰ、Ⅱ两部的面积的差是多少平方厘米?( =3.14)12、如下图,已知直角三角形的面积是12平方厘米,求阴影部分的面积。
13、如下图,O为圆心CO垂直于AB,三角形ABC的面积是45平方厘米,以C为圆心,CA为半径画弧将圆分成两部分,求阴影部分的面积。
14、如下图扇形的半径OA=OB=6厘米。
角AOB等于45°,AC垂直OB于C点,那么图中阴影部分面积是多少平方厘米?(π=3.14)15、下图中,图①是一个直径为3厘米的半圆,AB是直径,让A点不动,整个半圆逆时针旋转60°角,此时B 点移动到B′(如图②)。
那么,图中阴影部分的面积是多少平方厘米?(π=3.14)16、求下列图形的阴影部分。
17、下图中长方形的面积是45平方米,求阴影部分的面积。
18、把一块1.35公顷的长方形田地划分成两部分(如下图),其中三角形田地比梯形田地少0.81公顷,三角形的底是60米。

苏教版六年级数学下册几何图形专项全能训练1. 分针和时针的转速比是()。
A .1:12B .12:1C .60:12. 把一个圆柱削成一个最大的圆锥,削去部分的体积是这个圆柱体积的()A .B .C .2倍3. 油漆圆柱形柱子,要计算油漆的面积有多大,就是求()A .体积B .表面积C .侧面积4. 下列图形中,对称轴最多的是()A .圆B .正方形C .等边三角形D .半圆5. 在路灯下散步,当走向路灯时影子会()A .变长B .变短C .无法确定6. 俗话说:“饭后百步走,活到九十九.”靓靓晚上与爸爸在路灯下散步,当走向路灯时,他们的影子()A .会变长B .会变短C .长度保持不变7. 下面说法错误的是()A .圆是一种曲线图形B .半径一定比直径短C .圆是轴对称图形8. 一个圆锥的体积是6立方分米,与它等底、等高的圆柱的体积是()立方分米.A .2B .6C .189. 用一个高36厘米的圆锥形容器盛满水,倒入和它等底等高的圆柱形容器中,水的高度是()厘米.A .36B .18C .16D .1210. 一个圆锥与一个圆柱的底面积与体积分别相等,圆柱的高是9厘米,圆锥的高是()A .3厘米B .27厘米C .18厘米11. 如图的桌子上放着由几个小正方体摆成的图形.桌子的四周坐着四个小朋友,他们分别看到图形的一个面.小红看到的是______图,小军年到的是______图,小芳看到的是______图,小明看到的是______图.12. 李群在船快靠岸时,连续拍摄了几张图片,请你按先后顺序选择序号排列______。
13. 在同一个圆里,所有的______都相等.所有的______也都相等.14. 用小正方体拼一个立体图形,使其从左面看和从上面看分别得到下面的两个图形.要搭成这样的立体图形,最少需要______个小正方体,最多需要______个小正方体.15. 指针从B开始,顺时针旋转90°到______ .指针从B开始,逆时针旋转90°到______ .16. 你知道方格纸上图形的位置关系吗?①图形B可以看作图形A绕点______顺时针旋转90°得到的。

【练习1】【练习2】【练习3】【练习4】【练习5】【练习6】【练习7】【练习8】【练习9】【练习10】、相交于点;已知三角形与三角平方厘米,那么梯形的面积是平方厘【练习11】【练习12】,问阴影部分面积为多少?【练习13】【练习14】,三角形的面积为,那么三【练习15】【练习16】【练习17】【练习18】【练习19】【练习20】【练习21】【练习22】,则三角形的面积是.【练习23】【练习24】【练习25】【练习26】(取).【练习27】【练习28】【练习29】【练习30】平方厘米.【练习31】【练习32】【练习33】cm2,体积是cm【练习34】计算下面各圆锥体积(单位:厘米)(取)【练习35】【练习36】【练习1】【练习2】几何四边形一半模型等积变形【练习3】【练习4】,所以【练习5】【练习6】【练习7】【练习8】【练习9】:,所以【练习10】根据梯形中的蝴蝶模型(平方厘米),方厘米),故总面积为(平方厘米).蝴蝶模型【练习11】,根据蝴蝶模型和一半模型求出每一块的面积如图上标几何四边形蝴蝶模型基本梯形蝴蝶模型【练习12】如图,梯形面积为,四边形连接,在梯形中,;在梯形中,,并且四边形面积为,所以梯形空白部分的面积是,所以阴影的面积是【练习13】【练习14】.【练习15】【练习16】.【练习17】【练习18】平方厘米.【练习19】【练习20】【练习21】【练习22】,则三角形的面积是.可以看成三角形的“假高”(都是从顶点到底边连线,且两条“高”共线),【练习23】【练习24】【练习25】,【练习26】(取).【练习27】【练习28】【练习29】【练习30】平方厘米.【练习31】【练习32】【练习33】cm2,体积是cm(3)(4)【练习34】【练习35】【练习36】圆柱与圆锥圆柱与圆锥基本概念运用。


六年级数学下册图形与几何练习题班级考号姓名总分一、填空题。
1. 3.5平方米=()平方分米2立方分米3立方厘米=()立方分米5.02升=()升()毫升公顷=()平方米2.在钟面上,6时的时候,分针和时针所夹的角的度数是(),是一个()角。
3.一个三角形中,∠1=∠2=35°,∠3=(),按边分是()三角形。
4.一个三角形与一个平行四边形等底等高,如果三角形的面积是3.6平方分米,那么平行四边形的面积是()平方分米。
5.一个圆柱的底面直径是8厘米,高是1分米,它的侧面积是()平方厘米。
把它沿着底面直径垂直切成两半,表面积会增加()平方厘米。
6.三个棱长为2厘米的正方体拼成一个长方体,这个长方体的体积是()立方厘米,表面积是()平方厘米。
7.一个长方体相交于同一个顶点的三条棱的长度之比是3∶2∶1,这个长方体的棱长总和是72厘米。
长方体的表面积是()平方厘米,体积是()立方厘米。
8.一个圆柱和一个圆锥等底等高,圆柱与圆锥的体积之和是60立方厘米,圆柱的体积是()立方厘米,圆锥的体积是()立方厘米。
二、判断题。
(对的画“√”,错的画“✕”)1.平角是一条直线。
()2.三角形具有稳定性,四边形不具有稳定性。
()3.两个面积相等的梯形,可以拼成一个平行四边形。
()4.一个玻璃容器的体积与容积相等。
()5.一个棱长是6厘米的正方体的表面积和体积相等。
()三、选择题。
(把正确答案的序号填在括号里)1.射线()端点。
A.没有B.有一个C.有两个2.下面图形中对称轴最少的是()。
A.长方形B.正方形C.等腰梯形3.下面的立体图形从左边看到的图形是()。
4.下图中,甲和乙两部分面积的关系是()。
A.甲>乙B.甲<乙C.甲=乙5.一个圆柱的侧面展开图是一个正方形,这个圆柱的高与底面半径的比值是()。
A.πB.2πC.r四、计算题。
1.计算下面图形中阴影部分的面积。
(单位:厘米)2.计算以红色直线为轴旋转形成的立体图形的体积。

题号一二三四五六总分得分一、填空。
(18分,每空1分)1:一个三角形三条边的长度都是整厘米数,其中两条边分别是5cm和7cm,那么第三条边最长是()cm,最短是()cm。
2:在一个等腰三角形中,有一个角是100°,另外两个角的度数是()和(),它又是一个()角三角形。
3:一个梯形的面积是12cm²,如果它的上底、下底和高都分别扩大到原来的2倍,那么它现在的面积是()cm²。
4:瑶瑶在教室的座位是第3列第2排,用数对表示是(3,2),小森的座位是第2列第1排,用数对表示是(),小森向后调2排后的座位用数对表示是(,)。
5:一个平行四边形相邻两条边的长度分别是12cm和8cm,量得其中一条边上的高是10cm,这个平行四边形的面积是()cm²。
6:如图(1),把一个圆平均分成若干等份,然后把它剪拼成一个近似的长方形。
已知长方形的长是9.42cm,这个圆的周长是()cm,圆的面积是()cm²。
7:一根长1.5m的圆柱形木料,沿着横截面锯掉4dm长的一段后,表面积减少了0.5024m ²,这根木料原来的体积是()m³。
8:如图是(2)小蕾过生日时妈妈送给她的一个圆锥形的水晶饰品。
这个饰品的体积是()cm³,如果用一个长方形盒子包装它,这个盒子的体积至少是()cm³。
9:一个立体图形从正面看到的形状是,从左面看到的形状是,那么搭这样的立体图形最少需要()个小正方体,最多需要()个小正方体。
10:一个圆环,外圆周长是25.12m,内圆周长是6.28m,这个圆环宽()m,面积是()m²。
(1)(2)(4)二、判断。
(对的画“√”,错的画“×”)(5分)1:过一点只可以画一条直线。
()2:用放大镜看一个65°的角,看到的角变大了。
()3:圆柱的体积都是圆锥体积的3倍。
()4:长方形、正方形、平行四边形都是轴对称图形。
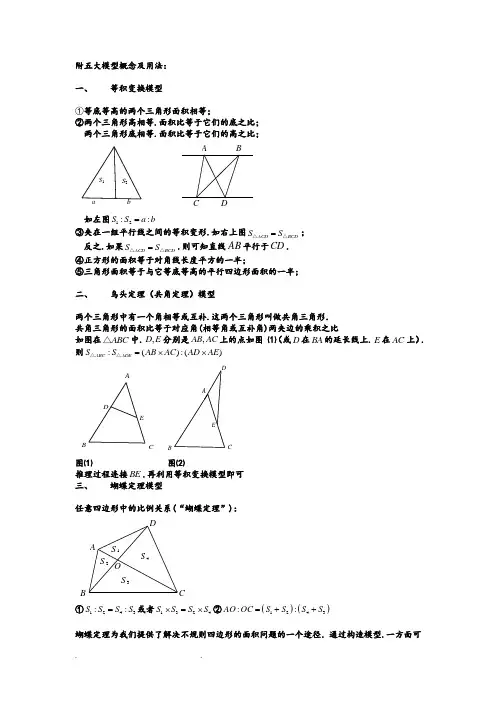
附五大模型概念及用法:一、 等积变换模型①等底等高的两个三角形面积相等;②两个三角形高相等.面积比等于它们的底之比; 两个三角形底相等.面积比等于它们的高之比;baS 2S 1 DC BA如左图12::S S a b =③夹在一组平行线之间的等积变形.如右上图ACD BCD S S =△△;反之.如果ACD BCD S S =△△.则可知直线AB 平行于CD . ④正方形的面积等于对角线长度平方的一半;⑤三角形面积等于与它等底等高的平行四边形面积的一半;二、 鸟头定理(共角定理)模型两个三角形中有一个角相等或互补.这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 如图在ABC △中.,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上.E 在AC 上).则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵推理过程连接BE .再利用等积变换模型即可 三、 蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型.一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面.也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝴蝶定理”):A BCDOba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③梯形S 的对应份数为()2a b +.四、 相似模型相似三角形性质:GF E ABCD (金字塔模型)ABCDEF G (沙漏模型)①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形.就是形状相同.大小不同的三角形(只要其形状不改变.不论大小怎样改变它们都相似).与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例.并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;五、 燕尾定理模型 S △ABG :S △AGC =S △BGE :S △EGC =BE :EC ;S △BGA :S △BGC =S △AGF :S △FGC =AF :FC ; S △AGC :S △BCG =S △ADG :S △DGB =AD :DB ;练习题集:1. (第3届华杯赛试题)一个长方形分成4个不同的三角形.绿色三角形面积是长方形面积的0.15倍.黄色三角形的面积是21平方厘米.问:长方形的面积是 平方厘米.红红绿黄21平方厘米2. (2007年六年级希望杯二试试题)如图.三角形田地中有两条小路AE 和CF .交叉处为D .张大伯常走这两条小路.他知道DF DC =,且2AD DE =.则两块地ACF 和CFB 的面积比是_________.F E DCBA3. 两条线段把三角形分为三个三角形和一个四边形.如图所示. 三个三角形的面积 分别是3.7.7.则阴影四边形的面积是多少?4. 如图.已知长方形ADEF 的面积16.三角形ADB 的面积是3.三角形ACF 的面积是4.那么三角形ABC 的面积是多少?F ED CB A5. (北京市第一届“迎春杯”刊赛)如图.将三角形ABC 的AB 边延长1倍到D .BC 边延长2倍到E .CA 边延长3倍到F .如果三角形ABC 的面积等于1.那么三角形DEF 的面积是 .FEDCB A6. 如图.在ABC △中.延长AB 至D ,使BD AB =.延长BC 至E ,使12CE BC =.F 是AC 的中点.若ABC △的面积是2.则DEF △的面积是多少?A BCDEF7. 如图.在ABC ∆中.已知M 、N 分别在边AC 、BC 上.BM 与AN 相交于O ,若AOM ∆、ABO ∆和BON ∆的面积分别是3、2、1.则MNC ∆的面积是 .8. 四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三角形BCD 的面积的13.且2AO =.3DO =.那么CO 的长度是DO 的长度的_________倍.9. 如右图.已知D 是BC 中点.E 是CD 的中点.F 是AC 的中点.ABC∆由这6部分组成.其中⑵比⑸大6平方厘米.那么ABC ∆的面积是多少平方厘米?10. 如右图.长方形ABCD 中.16EF =.9FG =.求AG 的长.D ABC EFGODCBANM OCBAFED CBA5()3()6()4()2()1()11. 如图.长方形ABCD 中.E 为AD 中点.AF 与BE 、BD 分别交于G 、H .已知5AH =cm .3HF =cm .求AG .12. 图中四边形ABCD 是边长为12cm 的正方形.从G 到正方形顶点C 、D 连成一个三角形.已知这个三角形在AB 上截得的EF 长度为4cm .那么三角形 GDC 的面积是多少?GF ED CBA13. 如右图.三角形ABC 中.BD :DC =4:9.CE :EA =4:3.求AF :FB .14. 如图.三角形ABC 的面积是1.BD =DE =EC .CF =FG =GA .三角形ABC 被分成9部分.请写出这9部分的面积各是多少?GFE D CBAOGH FE DC B A O F EDCB A15. 如右图.ABC △中.G 是AC 的中点.D 、E 、F 是BC 边上的四等分点.AD 与BG 交于M .AF 与BG 交于N .已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米.则ABC △的面积是多少平方厘米?N M GA BCD E F16. 如图.在正方形ABCD 中.E 、F 分别在BC 与CD 上.且2CE BE =.2CF DF =.连接BF .DE .相交于点G .过G 作MN .PQ 得到两个正方形MGQA 和正方形PCNG .设正方形MGQA 的面积为1S .正方形PCNG 的面积为2S .则12:S S =______.QPNM GFED CBA17. 如图.正方形ABCD 的边长为6.AE =1.5.CF =2.长方形EFGH 的面积为 .HGF EDCBA18. 如图.1ABC S =△.5BC BD =.4AC EC =.DG GS SE ==.AF FG =.求FGSS.SGF E DCBA19. 如图.在长方形ABCD 中.6AB =.2AD =.AE EF FB ==.求阴影部分的面积.D20. 如右图.已知BD DC =.2EC AE =.三角形ABC 的面积是30.求阴影部分面积.21. (第六届希望杯五年级一试)如图.正方形ABCD 的边长是12厘米.E 点在CD 上.BO AE 于O ,OB 长9厘米.则AE 长_________厘米。

小学六年级简单几何运动练习题题目一:图形变换1. 小明画了一个正方形,边长为5厘米。
他向右平移了3厘米,结果正方形变成了什么图形?2. 如果一个长方形的长度是8厘米,宽度是4厘米,小明将这个长方形向上平移了10厘米,结果是什么图形?3. 小红画了一个三角形,边长分别是3厘米,4厘米,5厘米。
小红将这个三角形向右平移了6厘米,结果是什么图形?题目二:图形旋转1. 小明画了一个正方形,边长为6厘米。
他将这个正方形顺时针旋转了90°,结果是什么图形?2. 如果一个长方形的长度是12厘米,宽度是8厘米,小明将这个长方形逆时针旋转了180°,结果是什么图形?3. 小红画了一个三角形,边长分别是5厘米,6厘米,7厘米。
小红将这个三角形逆时针旋转了120°,结果是什么图形?题目三:镜像对称1. 小明画了一个正方形,边长为7厘米。
他将这个正方形关于对称轴做了一次镜像对称,结果是什么图形?长方形关于对称轴做了两次镜像对称,结果是什么图形?3. 小红画了一个三角形,边长分别是6厘米,8厘米,10厘米。
小红将这个三角形关于对称轴做了三次镜像对称,结果是什么图形?题目四:图形组合1. 小明画了一个正方形,边长为4厘米。
他在正方形的上方粘贴了一个边长为3厘米的正方形,然后在这两个正方形的右边粘贴了一个边长为2厘米的正方形。
请问,这个图形一共有多少个正方形?2. 如果一个长方形的长度是12厘米,宽度是8厘米,小明将这个长方形上方粘贴了一个边长为5厘米的正方形,然后在这两个图形的左边粘贴了一个边长为3厘米的正方形。
请问,这个图形一共有多少个正方形?3. 小红画了一个三角形,边长分别是5厘米,6厘米,7厘米。
小红在这个三角形的上方粘贴了一个边长为4厘米的正方形,然后在这两个图形的右边粘贴了一个边长为3厘米的正方形。
请问,这个图形一共有多少个正方形?题目五:判断图形相等1. 小明画了一个正方形,边长为4厘米。
部编版六年级数学下册几何图形专项练习题1. 根据下面几幅图的排列规律,第四幅图是()A .B .C .D .2. 把一段圆柱形的木材,削成一个体积最大的圆锥,削去部分的体积是圆锥体积的()A .3倍B .C .D .2倍3. 在推导圆的面积公式时,用到平移或旋转。
4. 由图形(1)不能变为图形(2)的方法是()。
A .图形(1)绕“O”点逆时针方向旋转90°得到图形(2)B .图形(1)绕“O”点顺时针方向旋转90°得到图形(2)C .图形(1)绕“O”点逆时针方向旋转270°得到图形(2)D .以线段OP所在的直线为对称轴画图形(1)的轴对称图形得到图形(2)5. 把一个圆柱体的侧面展开得到一个边长4分米的正方形,这个圆柱体的侧面积是()平方分米.A .16B .50.24C .100.486. 按如下规律摆放三角形:则第(5)堆三角形的个数为()A .14B .15C .16D .177. 一个圆柱的侧面积是125.6平方米,高是10分米,它的体积是()立方分米.A .125.6B .1256C .12560D .12560008. 将一个周长12cm的正方形变换成面积为36cm2的正方形。
实际是按()的比放大的。
A .1:3B .2:1C .3:1D .4:19. 一个长方形操场长120米,宽60米,画在练习本上,选取()的比例尺比较合适.A .1:200B .1:2000C .1:10000D .1:40000010. 电风扇的运动是()A .平移B .旋转C .既平移又旋转11. 观察图形并填空。
①图1绕点“O”逆时针旋转90°到达图______的位置;②图1绕点“O”逆时针旋转180°到达图______的位置;③图1绕点“O”顺时针旋转______°到达图4的位置;④图2绕点“O”顺时针旋转______°到达图4的位置;⑤图2绕点“O”顺时针旋转90°到达图______的位置;⑥图4绕点“O”逆时针旋转90°到达图______的位置。
OABC1、一个小正方形,它的边长增加8厘米后,面积就增加了224平方厘米。
求小正方形的边长多少厘米。
(提示用方程解)2、如左图,已知长方形ABCD 的面积是88平方厘米,E 和F 分别是长和宽的中点。
(1)画出长方形ABCD 的所有对称轴。
(2)求出阴影部分的面积。
3、有一块长120米,宽80米的长方形空地,请你按一定的比例,画出空地的平面图,然后在平面图上用阴影标出41的草坪。
(注意:要标明你所采用的比例尺及相应的长和宽)。
4、圆的面积与长方形的面积相等,已知圆的周长62.8厘米,求阴影部分的周长。
5、一个圆柱底面直径是10厘米,高是20厘米,把圆柱的侧面沿着它的一条高剪开,再打开,然后按1:10的比例尺画出它的侧面展开图。
并标明数据。
的面积是求阴影部分的面积。
(单位:厘米)7、求图形中阴影部分的面积。
(单位:厘米)8、计算下面的阴影部分的面积。
(单位:厘米)9、已知四个等圆的半径分别为6厘米。
(1)求阴影部分的面积和周长。
(2)画出此图的所有对称轴。
10、画两个直径分别为3厘米和1厘米的同心圆,再画出这两个同心圆的两条互相垂直的对称轴。
并求出两个圆之间的环形部分的面积。
11、(1)在下面正方形内,画一个最大的圆,并标出圆心与半径。
(2)计算下面图形阴影部分的面积。
(4%)已知直径8厘米。
12、 (1)量出左图的直径是( )厘米。
(2)在圆内作一个最大正方形。
(3)以圆的直径为边长作一个正方形,使圆在正方形内。
(4)大正方形的周长是( )厘米。
(5)小正方形的面积是( )平方厘米。
FAB CD EO r23 21222。
六年级数学几何练习题在六年级数学学习的过程中,几何是一个重要的知识点。
通过几何的学习,可以培养学生的观察力、逻辑思维和空间想象能力。
下面是一些六年级数学几何练习题,帮助学生巩固和提升几何知识。
题一:判断图形1. 下面哪个图形是矩形?A. ◇B. △C. □D. ☆2. 下面哪个图形是正方形?A. ◇B. □C. ☆D. △3. 下面哪个图形是圆形?A. ◇B. □C. △D. ●4. 下面哪个图形是梯形?A. ◇B. □C. △D. ☆题二:计算图形的面积和周长根据下面的图形,计算其面积和周长。
1. 正方形的一边长为5 cm,计算它的面积和周长。
2. 长方形的长是8 cm,宽是4 cm,计算它的面积和周长。
3. 圆形的半径是6 cm,计算它的面积和周长。
(取π=3.14)4. 梯形的上底长是10 cm,下底长是8 cm,高是5 cm,计算它的面积和周长。
题三:比较图形大小1. 比较下面两个图形的面积:图形A:正方形,边长为6 cm图形B:长方形,长为5 cm,宽为8 cm2. 比较下面两个图形的周长:图形C:圆形,半径为7 cm(取π=3.14)图形D:矩形,长为9 cm,宽为5 cm题四:根据已知条件画图形1. 根据以下条件,画一个正方形:边长为4 cm2. 根据以下条件,画一个长方形:长为6 cm,宽为3 cm3. 根据以下条件,画一个圆形:半径为5 cm4. 根据以下条件,画一个梯形:上底为6 cm,下底为8 cm,高为4 cm通过以上的几何练习题,可以巩固六年级学生在数学几何方面的知识。
在解答练习题的过程中,学生需要观察图形的形状,并运用相关的面积和周长公式进行计算。
同时,根据给定条件画出相应的图形,培养学生的空间想象力和几何运算能力。
希望同学们能够通过这些练习题,掌握几何知识,提高数学水平。
六年级上册数学动手操作题一、题目。
1. 用圆规画一个半径为3厘米的圆,并求出它的周长和面积。
- 解析:- 画圆步骤:把圆规的两脚分开,定好两脚间的距离为3厘米(即半径);把有针尖的一只脚固定在一点(即圆心)上;把装有铅笔尖的一只脚旋转一周,就画出一个半径为3厘米的圆。
- 圆的周长公式C = 2π r(其中r为半径,π取3.14),则周长C=2×3.14×3 = 18.84厘米。
- 圆的面积公式S=π r^2,则面积S = 3.14×3^2=28.26平方厘米。
2. 画一个直径为4厘米的半圆,并求出它的周长和面积。
- 解析:- 画半圆步骤:先画一条长4厘米的线段作为半圆的直径;找到线段的中点作为圆心;以2厘米(半径)为半径,用圆规画半圆。
- 半圆的周长为圆周长的一半加上直径,圆的周长公式C = π d(d为直径),半圆周长C=(1)/(2)×3.14×4 + 4=10.28厘米。
- 半圆的面积为圆面积的一半,圆面积公式S=π r^2,半圆面积S=(1)/(2)×3.14×2^2=6.28平方厘米。
3. 在方格纸上(每个小方格边长为1厘米)画一个平行四边形,底为4厘米,高为3厘米。
- 解析:- 先在方格纸上确定一个点作为平行四边形的一个顶点,从这个顶点开始,沿着水平方向数4个小方格确定底的另一个端点;然后从底的一个端点向上垂直数3个小方格确定平行四边形的高的顶点;最后连接各点画出平行四边形。
4. 画一个三角形,底是5厘米,高是4厘米,并作出一条高。
- 解析:- 画三角形步骤:先画一条5厘米长的线段作为底;在底的一侧找到一点,从这点向底作一条垂直的线段,长度为4厘米,作为高;连接高的顶点与底的两个端点,得到三角形。
- 作高的方法:用三角板的一条直角边与三角形的底重合,另一条直角边过三角形相对的顶点,沿着这条直角边画线段就是三角形的高。
苏教版小学六年级解几何问题练习
在小学六年级数学课程中,几何问题是一个重要的内容。
通过解几何问题,学生可以培养空间想象力和逻辑推理能力,提高数学思维能力。
下面是一些苏教版小学六年级解几何问题的练,供学生们进行练和巩固。
题目一:画图
根据所给的条件,绘制下面的图形。
1. 给出一个三角形ABC,其中∠ABC = 90°,AD ⊥ BC,AE ⊥ AB。
连接BD、CE,证明△ADB ≌△AEC。
2. 给出一个长方形ABCD,对角线AC、BD交于点O。
连接OA、OB、OC、OD,证明四边形OABC为平行四边形。
题目二:计算
根据所给的条件和图形,计算下列问题。
1. 在正方形ABCD中,需要等分对角线AC,将AC分成两段长度相等的线段。
求分点E的坐标。
2. 在平行四边形ABCD中,已知∠D = 100°,求∠A的度数。
题目三:应用
根据所给的条件和图形,回答下列问题。
1. 若正方形的边长为8厘米,请计算其面积和周长。
2. 已知三角形ABC为等腰直角三角形,其中∠C = 90°,AB = 10厘米。
求∠A和∠B的度数。
以上是苏教版小学六年级解几何问题的练题目。
通过解答这些问题,学生们可以提升他们的几何思维能力和解决问题的能力。
希望这些练题能对学生们的研究有所帮助。
注意:计算题请写出详细的计算过程,以便学生们更好地理解解题思路。
人教版六年级数学下册《图形与几何》专项训练卷(附答案)1. 一个等腰三角形的一条边长为4cm,另一条边长为8cm,求这个等腰三角形的周长。
2. 钟面上,经过3小时,时针旋转了多少度?经过30分钟,分针旋转了多少度?3. 一个梯形的下底为18cm,下底缩短8cm后得到一个平行四边形,面积减少28cm2,原来梯形的面积是多少?4. 如图,直角梯形的周长为40cm,它的面积是多少?5. 一个长方体正好可以切成4个棱长为2cm的正方体,原长方体的棱长总和可能是多少?又可能是多少?6. 如图,一个圆柱和一个圆锥,圆柱的底面直径是圆锥的2倍,它们的高度相等。
一个这样的圆柱可以熔铸成多少个这样的圆锥?7. 观察下图,图①和图②中的三角形均为等边三角形,图①中小三角形的面积是大三角形面积的多少?③中小正方形的面积占大正方形面积的多少?8. 小明从一个长方体纸盒上撕下两个相邻的面(展开后如右图),这个纸盒的底面积是多少平方厘米,体积是多少立方厘米?9. 如下图所示,一张长方形铁皮,切割下阴影部分的两个圆和一个长方形刚好能做一个油桶,这个油桶的容积是多少L?10. 如图,圆的面积与长方形面积相等。
圆的周长是25.12cm,那么阴影部分的周长是多少?11. 图中正方形的面积是大于、等于还是小于平行四边形的面积?12. 用10倍的放大镜看40度的角,看到的角是多少度?13. 一个等腰三角形的一个底角是a度,它的顶角是多少度?14. 下列四个图形中,不能通过基本图形平移得到的是哪个?15. 如图,D、E分别是BC、AD边上的中点,那么阴影部分面积是ABC面积的多少?16. 一个平行四边形相邻的两边分别是8cm、10cm,其中一边上高是4cm,求这个平行四边形的面积。
答案:这个平行四边形的面积是36cm2。
2. 选B3. 选A4. 选C5. 选B6. 选D7. 选A8. 选C9. 选B10. 选C11. 选A12. 选C13. 选B14. 选D15. 选B16. 选C17. 无法呈现展开图,删除该题18. 改写:将大长方体切成两个完全一样的小长方体,每个小长方体的长、宽、高分别为5cm、2cm、1.5cm。
六年级数学几何操作题专项训练(总2页)
2
O
A B
C
1、一个小正方形,它的边长增加8厘米后,面积就增加了224平方厘米。
求小正方形的边长多少厘米。
(提示用方程解)
2、如左图,已知长方形ABCD 的面积是88平方厘米,E 和F 分别是长和宽的中点。
(1)画出长方形ABCD 的所有对称轴。
(2)求出阴影部分的面积。
3、有一块长120米,宽80米的长方形空地,请你按一定的比例,画出空地的平面图,然后在平面图上用阴影
标出4
1
的草坪。
(注意:要标明你所采用的比例尺及相
应的长和宽)。
4、圆的面积与长方形的面积相等,已知圆的周长厘米,求阴影部分的周长。
5、一个圆柱底面直径是10厘米,高是20厘米,把圆柱的侧面沿着它的一条高剪开,再打开,然后按1:10的比例尺画出它的侧面展开图。
并标明数据。
的面积是平方厘米,求阴影部分的面积。
(单位:厘米)
7、求图形中阴影部分的面积。
(单位:厘米)
8、计算下面的阴影部分的面积。
(单位:厘米)
9、已知四个等圆的半径分别为6厘米。
(1)求阴影部分的面积和周长。
(2)画出此图的所有对称轴。
10、画两个直径分别为3厘米和1厘米的同心圆,再画出这两个同心圆的两条互相垂直的对称轴。
并求出两个
圆之间的环形部分的面积。
11、(1)在下面正方形内,画一个最大的圆,并标出圆心与半径。
(2)计算下面图形阴影部分的面
积。
(4%)
已知直径8厘米。
F
A
B C
D E
O r 2
3 2 1
2
2
2
12、(1)量出左图的直径是()厘米。
正方形。
(3)以圆的直径为边长
作一个正方形,使圆在正方形
内。
(4)大正方形的周长是()厘米。
(5)小正方形的面积是()平方厘米。
3。