算法与程序框图复习题(含答案)

专题：算法与程序框图1.如下图,程序框图所进行的求和运算是( ) A.23111222+++ (1012)+ B.11123+++ ...110+ C.111+++ (118)+ D.111246+++ (120)+ 答案:D2.在可行域内任取一点,规则如下程序框图所示,则能输出数对(x,y)的概率为( )A.14B.2πC.4πD.8π 答案:C3.已知程序框图如下图所示,若输入n=6,则该程序运行的结果是( )A.2B.3C.4D.15 答案:B4.流程线的功能是( )A.表示算法的起始和结束B.表示算法输入和输出的信息C.赋值、计算D.按照算法的顺序连接程序框答案:D6.在一个算法中,如果需要反复执行某一处理步骤,最好采用的逻辑结构是( )A.顺序结构B.条件结构C.循环结构D.顺序结构或条件结构答案:C9.已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为1122()()x y x y ,,,,…()n n x y ,,,…(1)若程序运行中输出的一个数组是(9,t),则t= ;(2)程序结束时,共输出(x,y)的组数为 .答案:-4 1 00510.下边程序框图给出的程序执行后输出的结果是 .答案:244.下图是一个算法的程序框图,则输出S 的值是 .答案:63解析:2122+++…423133+=<,输出1+2+22+…+452263+=.2.如下程序框图,则最后输出的结果是( )A.5 049B.4 850C.2 450D.2 550答案:D4.如果下边程序运行后输出的结果是132,那么在程序中UNTIL 后面的“条件”应为( )A.i>11B.i>=11C.i<=11D.i<11答案:D6.阅读下边的程序框图,运行相应的程序,则输出s 的值为( )A.-1B.0C.1D.3答案:B解析:第一次运行程序时,i=1,s=3;第二次运行程序时,i=2,s=4;第三次运行程序时,i=3,s=1;第四次运行程序时,i=4,s=0,此时执行i=i+1后i=5,退出循环输出s=0.。

高一数学算法和程序框图试题答案及解析1.如图所示，程序框图（算法流程图）的输出结果是（）A．B．C．D．【答案】A【解析】条件成立，第一次执行循环体，条件成立，第二次执行循环体条件成立，第三次执行循环体；条件不成立，退出循环，输出.【考点】程序框图的识别和应用.2.若某程序图如图所示，则该程序运行后输出的k的值是（）A．4B．5C．6D．7【答案】B【解析】第一次执行循环体，.第二次执行循环体，,.第三次执行循环体，【考点】理解程序框图的逻辑结构.3.如下图所示程序框图，已知集合是程序框图中输出的值}，集合是程序框图中输出的值},全集U=Z，Z为整数集，当时，等于( )A．B．{-3. -1，5，7}C．{-3, -1，7}D．{-3, -1,7，9}【答案】D.【解析】依次执行程序框图中的语句：，；，；，；，；，；，；，；∴，，∴.【考点】读程序框图.4.在如图所示的程序框图中，输入A=192，B=22，则输出的结果是( ).A．0B．2C．4D．6【答案】B.【解析】本题要注意的是C是A除以B所得的余数，按程序框图可知有如下过程：原来：,第一次：C=16,A=22,B=16；第二次：C=6,A=16,B=6；第三次：C=4,A=6,B=4；第四次：C=2,A=4,B=2；第五次：C=0,A=2,B=0，此时B=0，则输出A=2，故选B.【考点】读懂程序框图的流程，赋值语句（如A=B，是把B的值赋值给A）.5.如果执行右边的程序框图，那么输出的（）A．22B．46C．94D．190【答案】C【解析】.运行第1次，=1，=1，=2，=4，=2＞5，否，循环；运行第2次，=3，=10，=3＞5，否，循环；运行第3次，=4，=22，=4＞5，否，循环；运行第4次，=5，=46，=5＞5，否，循环；运行第5次，=6，=94，=6＞5，是，输出S=94，故选C【考点】程序框图6.按右边程序框图运算：若，则运算进行几次才停止？A．B．C．D．【答案】C【解析】第一次循环，第二次循环，第三次循环，第四次循环，第五次循环。

数学算法和程序框图试题答案及解析1.运行如图所示的程序，若结束时输出的结果不小于3，则的取值范围为（）A．B．C．D．【答案】D【解析】第一次运行后,第二次运行后,第三次运行后,此时,停止循环,则,即.2.一个算法的程序框图如右图所示，若该程序输出的P位于区间内，则判断框内应填入的条件是（）A．B．C．D．【答案】C【解析】因为第一次循环，第二次循环，第三次循环，第四次循环，第五次循环，第六次循环，此时应结束循环，所以判断框中应填选C.【考点】程序框图3.执行如图所示的程序框图,输出的S值为时，则输入的的值为（）A．B．C．D．【答案】D【解析】在程序执行过程中，的值依次为；；；，程序结束，输出的S值为．故，即．【命题意图】本题考查程序框图基础知识，意在考查学生基本运算能力和逻辑推理能力. 4.已知函数y＝，写出求该函数函数值的算法及程序框图．【答案】见解析【解析】算法如下：第一步，输入x．第二步，如果x>0，则y＝－2；如果x＝0，则y＝0；如果x<0，则y＝2．第三步，输出函数值y．相应的程序框图如图所示．5.设计算法求＋＋＋…＋的值，并画出程序框图．【答案】见解析【解析】算法如下：第一步，令S＝0，i＝1；第二步，若i≤2 011成立，则执行第三步；否则，输出S，结束算法；第三步，S＝S＋；第四步，i＝i＋1，返回第二步．程序框图：6.根据下列算法语句, 当输入x为60时, 输出y的值为（）A．25B．30C．31D．61【答案】C【解析】,故选择C。

解答要注意条件的运用和判断。

【考点】本题考查算法程序，重点突出对条件语句的考查．是容易题。

7.如果执行右边的程序框图，输入正整数N(N≥2)和实数a1，a2，…，aN，输出A，B，则()A．A＋B为a1，a2，…，aN的和B．为a1，a2，…，aN的算术平均数C．A和B分别是a1，a2，…，aN中最大的数和最小的数D．A和B分别是a1，a2，…，aN中最小的数和最大的数【答案】C【解析】由程序框图可知，当x>A时，A＝x；当x≤A且x<B时，B＝x，所以A是a1，a2，…，a N 中的最大数，B是a1，a2，…，aN中的最小数．故选C．8.执行如图所示的程序框图，则输出的S值是()A．－1B．C．D．4【答案】A【解析】本小题主要考查程序框图的应用．解题的突破口为分析i与6的关系．当i＝1时，S＝＝－1；当i＝2时，S＝＝；当i＝3时，S＝＝；当i＝4时，S＝＝4；当i＝5时，S＝＝－1；当i＝6时程序终止，故而输出的结果为－1．9.程序框图如图所示，则该程序运行后输出的值是________．【答案】【解析】本题主要考查算法的程序框图及其应用．当i＝1时，T＝＝1，而i＝1＋1＝2，不满足条件i>5；接下来，当i＝2时，T＝，而i＝2＋1＝3，不满足条件i>5；接下来，当i＝3时，T ＝＝，而i＝3＋1＝4，不满足条件i>5；接下来，当i＝4时，T＝＝，而i＝4＋1＝5，不满足条件i>5；接下来，当i＝5时，T＝＝，而i＝5＋1＝6，满足条件i>5；此时输出T ＝，故应填．10.某程序框图如图所示，现将输出值依次记为：若程序运行中输出的一个数组是则数组中的（）A．32B．24C．18D．16【答案】A【解析】解:运行第一次,输出 , , ,运行第二次,输出运行第三次,输出运行第四次,输出运行第五次,输出运行第六次,输出所以选A．11.若如图所示的程序框图输出的S是30，则在判断框中M表示的“条件”应该是( ) A．B．C．D．【答案】B【解析】首先执行程序到,则应该填,故选B．12.某程序框图如图所示，若，则该程序运行后，输出的的值为（）A．33B．31C．29D．27【答案】B【解析】若，，则；；满足条件继续，；不满足条件，输出，结束．13.执行程序框图，则输出的S是（）A．5040B．4850C．2450D．2550【答案】C【解析】由程序框图分析可知：第一次循环：第二次循环：第三次循环：…，当时循环结束，此时，故输出的结果为2450，选C．14.某程序框图如图所示，该程序运行后输出的值是（）A．63B．31C．27D．15【答案】A【解析】程序框图运行如下：15.某程序框图如图所示，则该程序运行后输出的值为．【答案】7【解析】开始时，，进入循环，；，继续循环，；，继续循环，；，跳出循环，故．16.执行如图所示的算法流程图，则最后输出的等于．【答案】63【解析】第一次循环，第二次循环，第三次循环，第四次循环，第六次循环，终止循环，输出．17.若某程序框图如右图所示，则该程序运行后输出的值为．【答案】8【解析】，不满足是奇数，，不满足；，不满足是奇数，，不满足；，满足是奇数，，不满足；，不满足是奇数，，不满足；，不满足是奇数，，不满足；，不满足是奇数，，不满足；，不满足是奇数，，满足，输出．18.在下图算法框图中，若输入，程序运行的结果那么判断框中应填入的关于的判断条件是（）A．B．C．D．【答案】B．【解析】由，而输出，由程序框图使用列举法可得：，，结束算法，输出，因此判断框内条件应为“”故选B．【命题意图】本题考查定积分，算法框图中的顺序结构，条件结构、循环结构以及相应语句等基础知识，意在考查分析问题、解决问题的能力、基本运算能力及推理能力．19.对任意函数，，可按如图构造一个数列发生器，记由数列发生器产生数列{}．若定义函数，且输入，则数列{}的项构成的集合为（）A．B．C．D．【答案】C【解析】∵的定义域，把代入可得，把代入可得，把代入可得，因为，所以数列只有三项：，，．【命题意图】本题考查程序框图基础知识，意在考查学生基本运算能力和运算能力.20.如图所示,程序框图（算法流程图）的输出结果是，那么判断框中应填入的关于的判断条件是（）A．B．C．D．【答案】B【解析】经分析，此时满足题意，循环终止，故选B．【命题意图】本题主要考程序框图和循环结构等基础知识，意在考查学生是否理解和认识，并能利用程序框图解决问题的能力．。

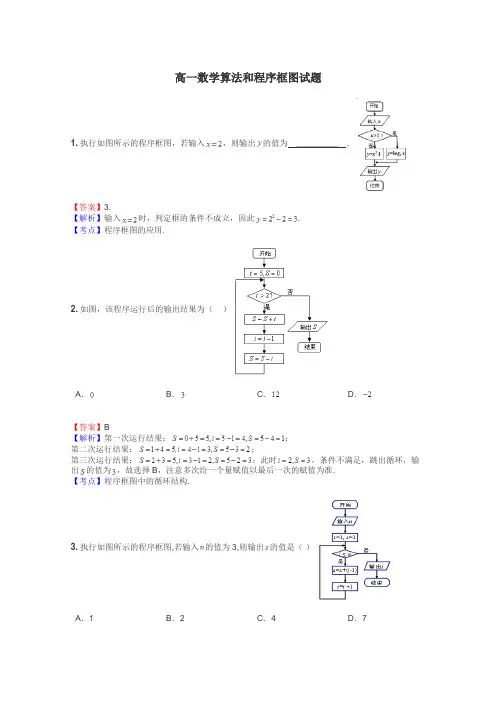
高一数学算法和程序框图试题1.执行如图所示的程序框图，若输入，则输出的值为_________．【答案】3.【解析】输入时，判定框的条件不成立，因此.【考点】程序框图的应用.2.如图，该程序运行后的输出结果为（）A．B．C．D．【答案】B【解析】第一次运行结果：；第二次运行结果：；第三次运行结果：；此时，条件不满足，跳出循环，输出的值为，故选择B，注意多次给一个量赋值以最后一次的赋值为准.【考点】程序框图中的循环结构.3.执行如图所示的程序框图,若输入的值为3,则输出的值是（）A．1B．2C．4D．7【答案】C【解析】当i=1时，S=1+1-1=1；当i=2时，S=1+2-1=2；当i=3时，S=2+3-1=4；当i=4时，退出循环，输出S=4；故选C．【考点】程序框图．4.某程序框图如图所示，若输入，则该程序运行后输出的值分别是（）A．B．C．D．【答案】A【解析】由框图的流程得：输入，，故输出【考点】算法和程序框图5.（12分）（1）已知函数，编写程序求函数值（只写程序）（2）画出程序框图：求和：（只画程序框图，循环体不对不得分）【答案】（1）程序详见试题解析；（2）详见试题解析．【解析】本题考查算法语句及算法框图，重点是循环结构的运用．（1）INPUT xIF x<0 THENy=2*x+1ELSEIF x<="1" THENy=x^3ELSEy=SQR(x)END IFEND IFPRINT yEND -----6分（2）程序框图略，循环体不对不得分 -----12分【考点】算法语句、算法框图．6.给出30个数：1，2，4，7，……，其规律是：第1个数是1，第2个数比第1个数大1, 第3个数比第2个数大2，第4个数比第3个数大3，依此类推.要计算这30个数的和，现已给出了该问题算法的程序框图（如图所示）（I）请在图中判断框内(1)处和执行框中的(2)处填上合适的语句，使之能完成该题算法功能；（II）根据程序框图写出程序.【答案】（I）（1）处应填i≤30；（2）处应填p=p+i.（II）略（参考解析）【解析】（I）判断语句的应用及当型循环程序的应用.（1）是控制循环的次数根据题意应该是30次.（2）中是要求30个数的累加和.（II）当型循环的程序的编写.按照格式编写.这是一个典型的求和程序的编写，要牢记.试题解析：（I）该算法使用了当型循环结构，因为是求30个数的和，故循环体应执行30次，其中i是计数变量，因此判断框内的条件就是限制计数变量i的，故应为i≤30.算法中的变量p实质是表示参与求和的各个数，由于它也是变化的，且满足第i个数比其前一个数大i-1，第i+1比其前一个数大i故应有p=p+i.故（1）处应填i≤30；（2）处应填p=p+i.(II)根据程序框图写出程序i=1p=1s=0WHILE i<=30s=s+pp=p+ii=i+1WENDPRINT s【考点】1.判断框的设置.2.当型循环程序的编写.7.运行如图所示的程序框图，则输出S的值为（）A．-2B．3C．4D．8【答案】A【解析】根据题意，由于起始量为n=1,s=1那么满足条件，可知s=0,n=2;依次得到s=2,n=3;s=-1,n=4;s=3,n=5;s=-2,n=6,此时终止循环得到s的值为-2，故答案为A【考点】程序框图点评：主要是考查了程序框图的运用，属于基础题。

高一数学算法和程序框图试题答案及解析1.如图是求样本平均数的程序框图，图中空白框中应填入的内容为（）A．B．C．S=S+n D．S=S+【答案】A【解析】由于，故第次循环为.【考点】程序框图的应用.2.下图为某算法的程序框图，则程序运行后输出的结果是（）A．2B．1C．3D．4【答案】C【解析】这里外是一个循环结构，一共循环了次，而内部是一个选择结构，根据条件确定的值是还是，然后把的值加给，次循环结束后，输出的值，便是正确答案，结果选择C.只要读懂题意，然后把人设想成计算机，按步骤逐步操作，最后就能得到正确答案.【考点】算法中的程序框图和循环结构与选择结构的嵌套.3.如图的程序框图，如果输入三个实数a，b，c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的( ).A．c＞x？B．x＞c？C．c＞b？D．b＞c？【答案】A.【解析】本题是寻找三个数中最大的数，在令a为x后，判断x与b的大小，因此第二个判断框里要判断的是x与c的大小，由于此时判断“是”时，c赋值为x，最后输出x，所以要填的是“c＞x？”.【考点】程序框图的理解与应用，填写判断框处的语句是常考的一个考点.4.按右边程序框图运算：若，则运算进行几次才停止？A．B．C．D．【答案】C【解析】第一次循环，第二次循环，第三次循环，第四次循环，第五次循环。

【考点】直到型循环程序框图。

5.执行如图所示的程序框图，如果输入，那么输出的a值为（）A．B．C．D．【答案】C【解析】根据程序框图的描述，是求使成立的最小a值，故选C．【考点】程序框图．6.执行下图的程序框图,若输入的x=2，则输出的y的值为【答案】23【解析】根据题意，本程序框图为求y的和循环体为“直到型”循环结构，输入x=2，第一次循环：y=2×2+1=5，x=5；第二次循环：y=2×5+1=11，x=11；第三次循环：y=2×11+1=23，∵|x-y|=12＞8，∴结束循环，输出y=23．故答案为：23．【考点】本题为程序框图题，考查对循环结构的理解和认识，按照循环结构运算后得出结果．属于基础题．7.若某程序框图如图所示，则输出的p的值是 ()A．30B．28C．21D．55【答案】A【解析】根据框图的循环结构，依次；；。

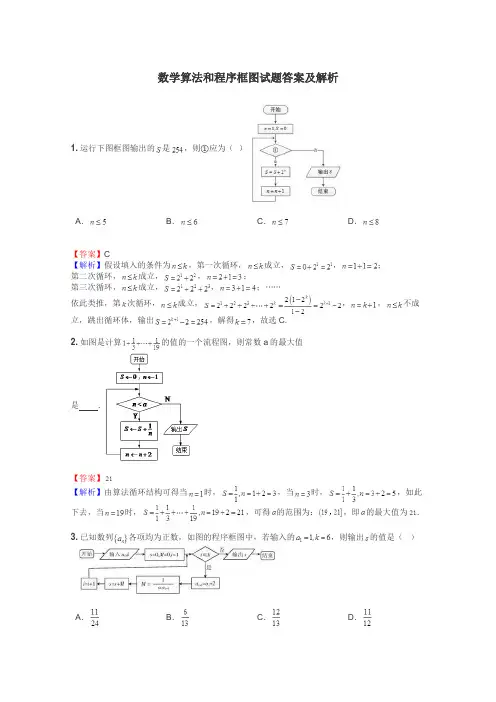
数学算法和程序框图试题答案及解析1.运行下图框图输出的是，则①应为（）A．B．C．D．【答案】C【解析】假设填入的条件为，第一次循环，成立，，；第二次循环，成立，，；第三次循环，成立，，；依此类推，第次循环，成立，，，不成立，跳出循环体，输出，解得，故选C.2.如图是计算的值的一个流程图，则常数a的最大值是．【答案】【解析】由算法循环结构可得当时，，当时，，如此下去，当时，，可得的范围为：，即的最大值为．3.已知数列各项均为正数，如图的程序框图中，若输入的，则输出的值是（）A．B．C．D．【答案】B．【解析】读程序框图可知数列通项公式，故选B．【考点】本题考查算法初步与程序框图、裂项法求数列的前项和等知识，意在考查读懂算法语句，进行简单计算的能力．4.执行如图所示的程序框图，输出的S值为（）A．1B．C．D．【答案】C【解析】第一次执行循环：,；第二次执行循环：,，满足≥2，结束循环，输出．【考点】本小题考查了对算法程序框图的三种逻辑结构的理解，考查了数据处理能力和算法思想的应用．5.如果执行如图所示的程序框图，输入x＝－1，n＝3，则输出的数S＝________．【答案】－4【解析】考查程序框图和数列的求和，考查考生的当型循环结构，关键是处理好循环次数，不要多加情况，或者少算次数．解决此类型试题，最好按循环依次写出结果．当i＝2时S＝－3，当i＝1时S＝5，当i＝0时S＝－4，当i＝－1时，不满足条件，退出循环，输出结果S＝－4．6.如图是用模拟方法估计圆周率π值的程序框图，P表示估计结果，则图中空白框内应填入()A．P＝B．P＝C．P＝D．P＝【答案】D【解析】本题主要考查循环结构的程序框图的应用，同时要兼顾考查学习概率的模拟方法中圆周率π的模拟，通过阅读题目和所给数据可知试验了1000次，M代表落在圆内的点的个数，根据几何概型，＝，对应的圆周率π为P＝．7.执行右面的程序框图，如果输入的n是4，则输出的P是A．8B．5C．3D．2【答案】C【解析】第一次执行结果：p="1,s=1,t=1,k=2;"第二次执行结果：p=2,s=1,t=2,k=3;第三次执行结果：p=3,s=2,t=3,k=4;结束循环，输出p的值4．8.执行右面的程序框图，如果输入的N是6，那么输出的是（）A．120B．720C．1440D．5040【答案】B【解析】B按照算法的程序化思想，有程序框图执行下面的计算可得：，此时，按终止条件结束，输出9.程序框图如图所示：如果上述程序运行的结果S＝1320，那么判断框中应填入( )A．K＜10！B．K≤10！C．K＜9? ！D．K≤11！【答案】A【解析】以此运行循环语句直到S＝1320,可得判断框中应填入K＜10！,故选A．10.右面是“二分法”解方程的流程图．在①~④处应填写的内容分别是( )A．f(a)f(m)<0；a=m；是；否B．f(b)f(m)<0；b=m；是；否C．f(b)f(m)<0；m=b；是；否D．f(b)f(m)<0；b=m；否；是【答案】B【解析】根据二分法的概念可知选B．11.在数列中，．为计算这个数列前10项的和，现给出该问题算法的程序框图（如图所示），则图中判断框（1）处合适的语句是 ( )A．B．C．D．【答案】C【解析】因为当i=0时运算的结果为s=1，当i=1时运算的结果为s=1+3,所以当i=10时输出前10项的和．12.某程序框图如图所示，现输入如下四个函数，则可以输出的函数是（）A．B．C．D．【答案】D【解析】∵A和C中的函数不是奇函数，不满足条件，故排除A、C；又∵中的函数图象与轴没有交点，不存在零点，而D中既是奇函数，而且函数图象与也有交点，故D符合输出的条件，故选D．13.运行如图所示的程序框图，若输出的是，则①应为（）A．n≤5B．n≤6C．n≤7D．n≤8【答案】C【解析】由程序框图算法可知，，由于输出，即，解得，故①应为“”，故选14.执行如图所示的程序框图．若输入，则输出的值是( )A．B．C．D．【答案】C【解析】这是一个循环结构，循环的结果依次为：．最后输出5．15.运行右图所示框图的相应程序,若输入的值分别为和,则输出的值是（）A．0B．1C．2D．－1【答案】C【解析】因为，，所以，由算法框图可知，运行后输出的值为．16.若某程序框图如右图所示，则该程序运行后输出的值为．【答案】8【解析】，不满足是奇数，，不满足；，不满足是奇数，，不满足；，满足是奇数，，不满足；，不满足是奇数，，不满足；，不满足是奇数，，不满足；，不满足是奇数，，不满足；，不满足是奇数，，满足，输出．17.某店一个月的收入和支出总共记录了 N个数据，，。

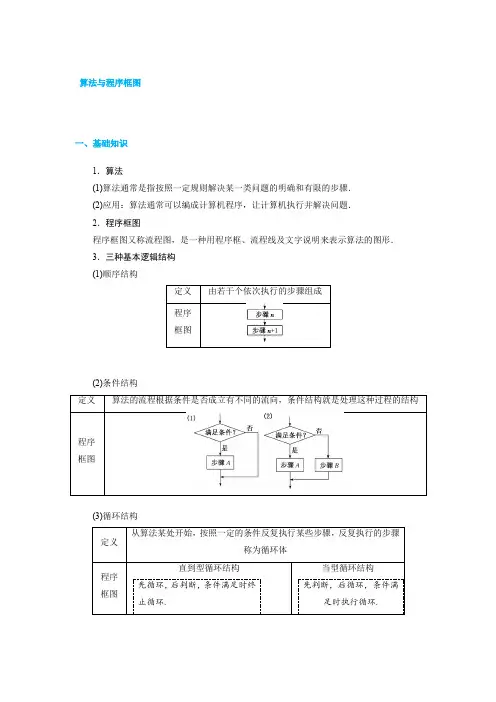
算法与程序框图一、基础知识1．算法(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤． (2)应用：算法通常可以编成计算机程序，让计算机执行并解决问题． 2．程序框图程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形． 3．三种基本逻辑结构 (1)顺序结构(2)条件结构(3)循环结构三种基本逻辑结构的适用情境(1)顺序结构：要解决的问题不需要分类讨论． (2)条件结构：要解决的问题需要分类讨论．(3)循环结构：要解决的问题要进行许多重复的步骤，且这些步骤之间有相同的规律．考点一 顺序结构和条件结构[例1] (2019·沈阳质检)已知一个算法的程序框图如图所示，当输出的结果为0时，输入的实数x 的值为( )A ．－3B ．－3或9C ．3或－9D ．－3或－9[解析] 当x ≤0时，y ＝⎝⎛⎭⎫12x －8＝0，x ＝－3；当x >0时，y ＝2－log 3x ＝0，x ＝9.故x ＝－3或x ＝9，选B.[答案] B[例2] 某程序框图如图所示，现输入如下四个函数，则可以输出的函数为( )A ．f (x )＝cos x x ⎝⎛⎭⎫－π2<x <π2，且x ≠0 B ．f (x )＝2x －12x ＋1C ．f (x )＝|x |xD ．f (x )＝x 2ln(x 2＋1)[解析] 由程序框图知该程序输出的是存在零点的奇函数，选项A 、C 中的函数虽然是奇函数，但在给定区间上不存在零点，故排除A 、C.选项D 中的函数是偶函数，故排除D.选B.[答案] B[解题技法] 顺序结构和条件结构的运算方法(1)顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的．解决此类问题，只需分清运算步骤，赋值量及其范围进行逐步运算即可．(2)条件结构中条件的判断关键是明确条件结构的功能，然后根据“是”的分支成立的条件进行判断．(3)对于条件结构，无论判断框中的条件是否成立，都只能执行两个分支中的一个，不能同时执行两个分支．[题组训练]1．半径为r 的圆的面积公式为S ＝πr 2，当r ＝5时，计算面积的流程图为( )解析：选D 因为输入和输出框是平行四边形，故计算面积的流程图为D. 2．运行如图所示的程序框图，可输出B ＝______，C ＝______.解析：若直线x＋By＋C＝0与直线x＋3y－2＝0平行，则B＝3，且C≠－2，若直线x＋3y＋C＝0与圆x2＋y2＝1相切，则|C|12＋(3)2＝1，解得C＝±2，又C≠－2，所以C＝2.答案：3 2考点二循环结构考法(一)由程序框图求输出(输入)结果[例1](2018·天津高考)阅读如图所示的程序框图，运行相应的程序，若输入N的值为20，则输出T的值为()A．1B．2C．3 D．4[解析]输入N的值为20，第一次执行条件语句，N＝20，i ＝2，Ni ＝10是整数，∴T ＝0＋1＝1，i ＝3＜5；第二次执行条件语句，N ＝20，i ＝3，N i ＝203不是整数，∴i ＝4＜5；第三次执行条件语句，N ＝20，i ＝4，Ni ＝5是整数，∴T ＝1＋1＝2，i ＝5，此时i ≥5成立，∴输出T ＝2. [答案] B[例2] (2019·安徽知名示范高中联考)执行如图所示的程序框图，如果输出的n ＝2，那么输入的 a 的值可以为( )A ．4B ．5C ．6D ．7[解析] 执行程序框图，输入a ，P ＝0，Q ＝1，n ＝0，此时P ≤Q 成立，P ＝1，Q ＝3，n ＝1，此时P ≤Q 成立，P ＝1＋a ，Q ＝7，n ＝2.因为输出的n 的值为2，所以应该退出循环，即P >Q ，所以1＋a >7，结合选项，可知a 的值可以为7，故选D.[答案] D[解题技法] 循环结构的一般思维分析过程 (1)分析进入或退出循环体的条件，确定循环次数．(2)结合初始条件和输出结果，分析控制循环的变量应满足的条件或累加、累乘的变量的表达式．(3)辨析循环结构的功能． 考法(二) 完善程序框图[例1] (2018·武昌调研考试)执行如图所示的程序框图，如果输入的a 依次为2,2,5时，输出的s 为17，那么在判断框中可以填入( )A ．k <n?B ．k >n?C ．k ≥n?D ．k ≤n?[解析] 执行程序框图，输入的a ＝2，s ＝0×2＋2＝2，k ＝1；输入的a ＝2，s ＝2×2＋2＝6，k ＝2；输入的a ＝5，s ＝2×6＋5＝17，k ＝3，此时结束循环，又n ＝2，所以判断框中可以填“k >n ？”，故选B.[答案] B[例2] (2018·全国卷Ⅱ)为计算S ＝1－12＋13－14＋…＋199－1100，设计了如图所示的程序框图，则在空白框中应填入( )A ．i ＝i ＋1B ．i ＝i ＋2C ．i ＝i ＋3D ．i ＝i ＋4[解析] 由题意可将S 变形为S ＝⎝⎛⎭⎫1＋13＋…＋199－⎝⎛⎭⎫12＋14＋…＋1100，则由S ＝N －T ，得N ＝1＋13＋…＋199，T ＝12＋14＋…＋1100.据此，结合N ＝N ＋1i ，T ＝T ＋1i ＋1易知在空白框中应填入i ＝i ＋2.故选B.[答案] B[解题技法] 程序框图完善问题的求解方法(1)先假设参数的判断条件满足或不满足；(2)运行循环结构，一直到运行结果与题目要求的输出结果相同为止； (3)根据此时各个变量的值，补全程序框图．[题组训练]1．(2018·凉山质检)执行如图所示的程序框图，设输出的数据构成的集合为A ，从集合A 中任取一个元素a ，则函数y ＝x a ，x ∈[0，＋∞)是增函数的概率为( )A.47B.45C.35D.34解析：选C 执行程序框图，x ＝－3，y ＝3；x ＝－2，y ＝0；x ＝－1，y ＝－1；x ＝0，y ＝0；x ＝1，y ＝3；x ＝2，y ＝8；x ＝3，y ＝15；x ＝4，退出循环．则集合A 中的元素有－1,0,3,8,15，共5个，若函数y ＝x a ，x ∈[0，＋∞)为增函数，则a >0，所以所求的概率为35.2．(2019·珠海三校联考)执行如图所示的程序框图，若输出的n 的值为4，则p 的取值范围是( )A.⎝⎛⎦⎤34，78B.⎝⎛⎭⎫516，＋∞C.⎣⎡⎭⎫516，78D.⎝⎛⎦⎤516，78解析：选A S ＝0，n ＝1；S ＝12，n ＝2；S ＝12＋122＝34，n ＝3；满足条件，所以p >34，继续执行循环体；S ＝34＋123＝78，n ＝4；不满足条件，所以p ≤78.输出的n 的值为4，所以34<p ≤78，故选A.3．(2019·贵阳适应性考试)某程序框图如图所示，若该程序运行后输出的值是137，则整数a 的值为( )A ．6B ．7C ．8D ．9解析：选A 先不管a 的取值，直接运行程序．首先给变量S ，k 赋值，S ＝1，k ＝1，执行S ＝S ＋1k (k ＋1)，得S ＝1＋11×2，k ＝2；执行S ＝1＋11×2＋12×3，k ＝3；……继续执行，得S ＝1＋11×2＋12×3＋…＋1k (k ＋1)＝1＋⎝⎛⎭⎫1－12＋⎝⎛⎭⎫12－13＋…＋⎝⎛⎭⎫1k －1k ＋1＝2－1k ＋1，由2－1k ＋1＝137得k ＝6，所以整数a ＝6，故选A.考点三 基本算法语句[典例] 执行如图程序语句，输入a ＝2cos 2 019π3，b ＝2tan 2 019π4，则输出y 的值是( )A ．3B ．4C ．6D ．－1[解析] 根据条件语句可知程序运行后是计算y ＝⎩⎪⎨⎪⎧a (a ＋b )，a <b ，a 2－b ，a ≥b ，且a ＝2cos 2 019π3＝2cos π＝－2，b ＝2tan 2 019π4＝2tan 3π4＝－2.因为a ≥b ，所以y ＝a 2－b ＝(－2)2－(－2)＝6， 即输出y 的值是6. [答案] C[变透练清]1. 执行如图所示的程序，输出的结果是________．i ＝11S ＝1DOS ＝S*ii ＝i －1LOOP UNTIL i<9PRINT S END解析：程序反映出的算法过程为 i ＝11⇒S ＝11×1，i ＝10； i ＝10⇒S ＝11×10，i ＝9； i ＝9⇒S ＝11×10×9，i ＝8；i ＝8<9退出循环，执行“PRINT S ”． 故S ＝990. 答案：9902．阅读如图所示的程序．a 的值是________． 解析：由题意可得程序的功能是计算并输出a ＝⎩⎪⎨⎪⎧2＋a ，a >2，a ×a ，a ≤2的值， 当a >2时，由2＋a ＝9得a ＝7； 当a ≤2时，由a 2＝9得a ＝－3， 综上知，a ＝7或a ＝－3. 答案：－3或7[课时跟踪检测]1．(2019·湖北八校联考)对任意非零实数a ，b ，定义a *b 的运算原理如图所示，则(log222)*⎝⎛⎭⎫18－23＝( )A ．1B ．2C ．3D ．4解析：选A 因为log222＝3，⎝⎛⎭⎫18－23＝4,3<4，所以输出4－13＝1，故选A. 2．执行如图所示的程序框图，则输出的x ，y 分别为( )A ．90,86B ．94,82C ．98,78D ．102,74解析：选C 第一次执行循环体，y ＝90，s ＝867＋15，不满足退出循环的条件，故x ＝90；第二次执行循环体，y ＝86，s ＝907＋433，不满足退出循环的条件，故x ＝94；第三次执行循环体，y ＝82，s ＝947＋413，不满足退出循环的条件，故x ＝98；第四次执行循环体，y ＝78，s ＝27，满足退出循环的条件，故x ＝98，y ＝78.3．(2018·云南民族大学附属中学二模)执行如图所示的程序框图，若输出的k 的值为6，则判断框内可填入的条件是( )A ．s >12？B ．s >710？C ．s >35？D ．s >45？解析：选B s ＝1，k ＝9，满足条件；s ＝910，k ＝8，满足条件；s ＝45，k ＝7，满足条件；s ＝710，k ＝6，不满足条件．输出的k ＝6，所以判断框内可填入的条件是“s >710？”．故选B.4．(2019·合肥质检)执行如图所示的程序框图，如果输出的k 的值为3，则输入的a 的值可以是( )A ．20B ．21C ．22D ．23解析：选A 根据程序框图可知，若输出的k ＝3，则此时程序框图中的循环结构执行了3次，执行第1次时，S ＝2×0＋3＝3，执行第2次时，S ＝2×3＋3＝9，执行第3次时，S ＝2×9＋3＝21，因此符合题意的实数a 的取值范围是9≤a <21，故选A.5．(2019·重庆质检)执行如图所示的程序框图，如果输入的x ＝0，y ＝－1，n ＝1，则输出x ，y 的值满足( )A ．y ＝－2xB ．y ＝－3xC ．y ＝－4xD ．y ＝－8x解析：选C 初始值x ＝0，y ＝－1，n ＝1，x ＝0，y ＝－1，x 2＋y 2<36，n ＝2，x ＝12，y＝－2，x 2＋y 2<36，n ＝3，x ＝32，y ＝－6，x 2＋y 2>36，退出循环，输出x ＝32，y ＝－6，此时x ，y 满足y ＝－4x ，故选C.6．(2018·南宁二中、柳州高中联考)执行如图所示的程序框图，若输出的结果s ＝132，则判断框中可以填( )A．i≥10? B．i≥11?C．i≤11? D．i≥12?解析：选B执行程序框图，i＝12，s＝1；s＝12×1＝12，i＝11；s＝12×11＝132，i ＝10.此时输出的s＝132，则判断框中可以填“i≥11？”．7．(2019·漳州八校联考)执行如图所示的程序，若输出的y的值为1，则输入的x的值为() INPUT xIF x>＝1THENy＝x2ELSEy＝－x2＋1END IFPRINT yENDA．0 B．1C．0或1 D．－1,0或1解析：选C当x≥1时，由x2＝1得x＝1或x＝－1(舍去)；当x<1时，由－x2＋1＝1得x＝0.∴输入的x的值为0或1.)8．执行如图所示的程序框图，若输入的n＝4，则输出的s＝(C．20 D．35解析：选C执行程序框图，第一次循环，得s＝4，i＝2；第二次循环，得s ＝10，i ＝3； 第三次循环，得s ＝16，i ＝4； 第四次循环，得s ＝20，i ＝5.不满足i ≤n ，退出循环，输出的s ＝20.9.(2018·洛阳第一次统考)已知某算法的程序框图如图所示，则该算法的功能是( )A ．求首项为1，公差为2的等差数列的前2 018项和B ．求首项为1，公差为2的等差数列的前2 019项和C ．求首项为1，公差为4的等差数列的前1 009项和D ．求首项为1，公差为4的等差数列的前1 010项和解析：选D 由程序框图得，输出的S ＝(2×1－1)＋(2×3－1)＋(2×5－1)＋…＋(2×2 019－1)，可看作数列{2n －1}的前2 019项中所有奇数项的和，即首项为1，公差为4的等差数列的前1 010项和．故选D.10．(2018·郑州第一次质量测试)执行如图所示的程序框图，若输出的结果是7，则判断框内m 的取值范围是( )A ．(30,42]B ．(30,42)C ．(42,56]D ．(42,56)解析：选A k ＝1，S ＝2，k ＝2；S ＝2＋4＝6，k ＝3；S ＝6＋6＝12，k ＝4；S ＝12＋8＝20，k ＝5；S ＝20＋10＝30，k ＝6；S ＝30＋12＝42，k ＝7，此时不满足S ＝42<m ，退出循环，所以30<m ≤42，故选A.11．(2019·石家庄调研)20世纪70年代，流行一种游戏——角谷猜想，规则如下：任意写出一个自然数n ，按照以下的规律进行变换，如果n 是奇数，则下一步变成3n ＋1；如果n 是偶数，则下一步变成n2.这种游戏的魅力在于无论你写出一个多么庞大的数字，最后必然会落在谷底，更准确地说是落入底部的4－2－1循环，而永远也跳不出这个圈子，下列程序框图就是根据这个游戏而设计的，如果输出的i 值为6，则输入的n 值为( )A ．5或16B ．16C ．5或32D ．4或5或32解析：选C 若n ＝5，执行程序框图，n ＝16，i ＝2；n ＝8，i ＝3；n ＝4，i ＝4；n ＝2，i ＝5；n ＝1，i ＝6，结束循环，输出的i ＝6.若n ＝32，执行程序框图，n ＝16，i ＝2；n ＝8，i ＝3；n ＝4，i ＝4；n ＝2，i ＝5；n ＝1，i ＝6，结束循环，输出的i ＝6.当n ＝4或16时，检验可知不正确，故输入的n ＝5或32，故选C.12．(2018·贵阳第一学期检测)我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目：“一百馒头一百僧，大僧三个更无争．小僧三人分一个，大小和尚各几丁？”如图所示的程序框图反映了对此题的一个求解算法，则输出的n 的值为( )A ．20B ．25C ．30D ．35解析：选B 法一：执行程序框图，n ＝20，m ＝80，S ＝60＋803＝8623≠100；n ＝21，m ＝79，S ＝63＋793＝8913≠100；n ＝22，m ＝78，S ＝66＋783＝92≠100；n ＝23，m ＝77，S ＝69＋773＝9423≠100；n ＝24，m ＝76，S ＝72＋763＝9713≠100；n ＝25，m ＝75，S ＝75＋753＝100，退出循环．所以输出的n ＝25.法二：设大和尚有x 个，小和尚有y 个， 则⎩⎪⎨⎪⎧x ＋y ＝100，3x ＋13y ＝100，解得⎩⎪⎨⎪⎧x ＝25，y ＝75， 根据程序框图可知，n 的值即大和尚的人数，所以n ＝25.13．已知函数y ＝lg|x －3|，如图所示程序框图表示的是给定x 值，求其相应函数值y 的算法．请将该程序框图补充完整．其中①处应填________，②处应填________．解析：由y ＝lg|x －3|＝⎩⎪⎨⎪⎧lg (x －3)，x >3，lg (3－x )，x <3及程序框图知，①处应填x <3？，②处应填y＝lg(x －3)．答案：x <3？ y ＝lg(x －3)14．执行如图所示的程序框图，若输入的N ＝20，则输出的S ＝________.解析：依题意，结合题中的程序框图知，当输入的N ＝20时，输出S 的值是数列{2k －1}的前19项和，即19(1＋37)2＝361.答案：36115．执行如图所示的程序框图，则输出的λ是________．解析：依题意，若λa ＋b 与b 垂直，则有(λa ＋b )·b ＝4(λ＋4)－2(－3λ－2)＝0，解得λ＝－2；若λa ＋b 与b 平行，则有－2(λ＋4)＝4(－3λ－2)，解得λ＝0.结合题中的程序框图可知，输出的λ是－2.答案：－216．执行如图所示的程序框图，如果输入的x ，y ∈R ，那么输出的S 的最大值为________．解析：当条件x ≥0，y ≥0，x ＋y ≤1不成立时，输出S 的值为1，当条件x ≥0，y ≥0，x ＋y ≤1成立时，输出S ＝2x ＋y ，下面用线性规划的方法求此时S 的最大值．作出不等式组⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋y ≤1表示的平面区域如图中阴影部分所示，由图可知当直线S ＝2x ＋y 经过点M (1,0)时S 最大，其最大值为2×1＋0＝2，故输出S 的最大值为2.答案：2。

高二数学算法和程序框图试题1.执行如图所示的程序框图，若输出，则框图中①处可以填入（）A．B．C．D．【答案】C【解析】程序在运行过程中各变量的值如下表示：是否继续循环 S n循环前/0 1第一次是 1 2第二次是 3 4第三次是 7 8第四次是 15 16，因为输出：S=15．所以判断框内可填写“n＞8”，故选：B．【考点】程序框图．2.已知某程序框图如图所示，则执行该程序后输出的结果是（）.A．B．C．2D．1【答案】A【解析】由程序框图得：，即输出的值具有周期性，最小正周期为3，且,所以输出的值为.【考点】程序框图.3.给出如图的程序框图，则输出的数值是（）.A．B．C．D．【答案】A【解析】该程序框图的功能是计算的值；因为所以输出的数值是.【考点】程序框图、裂项抵消法求和.4.执行如图的程序框图，输出S的值为( ).A．1B．2C．3D．4【答案】B【解析】该程序框图的功能是计算的值，故选B.【考点】程序框图.5.执行如图的程序框图，若输出的，则输入整数的最大值是（）A．15B．14C．7D．6【答案】A【解析】初始值：成立，运行第一次成立，运行第二次成立，运行第三次成立，运行第四次不成立，循环终止，输出输入整数的最大值是15.故选A.【考点】循环结构.6.如图是向量运算的知识结构图，如果要加入“向量共线的充要条件”，则应该是在____的下位．【答案】数乘.【解析】知识结构图的作用是用图形直观地再现出知识之间的关联，由于向量共线的充要条件是向量数乘中的一种，故在知识结构图中，向量共线的充要条件应该放在数乘的下位．【考点】结构图．7.按流程图的程序计算，若开始输入的值为=2，则输出的的值是（）A．3B．6C．21D．156【答案】C【解析】第一次运行，计算，不成立，往否的方向进行；第二次运行，计算，不成立，往否的方向进行；第三次运行，计算，不成立，往否的方向进行；第四次运行，计算，成立，往是的方向进行；输出。

第一章 算法初步1.1算法与程序框图 1。

1.1算法的概念1。

已知直角三角形两直角边长为a ，b ,求斜边长c 的一个算法分下列三步: ①计算22c a b =+a ，b 的值;③输出斜边长c 的值,其中正确的顺序是 【 】 A.①②③ B。

②③① C。

①③② D。

②①③2。

若()f x 在区间[],a b 内单调,且()()0f a f b <，则()f x 在区间[],a b 内 【 】 A.至多有一个根 B.至少有一个根 C 。

恰好有一个根 D 。

不确定3.已知一个学生的语文成绩为89，数学成绩为96,外语成绩为99。

求他的总分和平均成绩的一个算法为：第一步：取A =89 ,B =96 ，C =99； 第二步：____①______； 第三步：_____②_____； 第四步:输出计算的结果。

4。

写出按从小到大的顺序重新排列,,x y z 三个数值的算法.1．1．2 程序框图1．在程序框图中，算法中间要处理数据或计算，可分别写在不同的 【 】 A ．处理框内 B ．判断框内 C ．终端框内 D ．输入输出框内2．将两个数a=10，b=18交换，使a=18,b=10，下面语句正确一组是 【 】A. B. C. D 。

a=c=b b=aa=c b=a=c c=b b=a3指出下列语句的错误，并改正:（1)A=B=50（2）x=1，y=2，z=3（3）INPUT “How old are y ou” x（4）INPUT ，x（5）PRINT A+B=；C(6)PRINT Good—b y e!4．2000年我国人口为13亿，如果人口每年的自然增长率为7‰,那么多少年后我国人口将达到15亿？设计一个算法的程序。

5。

儿童乘坐火车时,若身高不超过1。

1 m，则不需买票;若身高超过1。

1 m但不超过1.4 m，则需买半票；若身高超过1。

4 m，则需买全票。

试设计一个买票的算法，并画出相应的程序框图及程序.1.2基本算法语句1.2。

第一章 算法初步1.1算法与程序框图1.1.1算法的概念1.已知直角三角形两直角边长为a ,b ,求斜边长c 的一个算法分下列三步:①计算22c a b =+a ,b 的值；③输出斜边长c 的值,其中正确的顺序是 【 】A.①②③B.②③①C.①③②D.②①③2.若()f x 在区间[],a b 内单调,且()()0f a f b <,则()f x 在区间[],a b 内 【 】A.至多有一个根B.至少有一个根C.恰好有一个根D.不确定3.已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99.求他的总分和平均成绩的一个算法为: 第一步:取A =89 ,B =96 ,C =99；第二步:____①______；第三步:_____②_____；第四步:输出计算的结果.4.写出按从小到大的顺序重新排列,,x y z 三个数值的算法.1．1．2 程序框图1．在程序框图中，算法中间要处理数据或计算，可分别写在不同的 【 】A ．处理框内B ．判断框内C ．终端框内D ．输入输出框内2．将两个数a=10，b=18交换，使a=18，b=10，下面语句正确一组是 【 】A. B. C. D.3指出下列语句的错误，并改正:(1)A =B =50(2)x =1，y =2，z =3(3)INPUT “How o ld are y ou” x(4)INPUT ，x(5)PRINT A +B =；C(6)PRINT Good-b y e!4．2021年我国人口为13亿，如果人口每年的自然增长率为7‰，那么多少年后我国人口将达到15亿？设计一个算法的程序.5.儿童乘坐火车时，若身高不超过1.1 m ，则不需买票；若身高超过1.1 m 但不超过1.4 m ，则需买半票；若身高超过1.4 m ，则需买全票.试设计一个买票的算法，并画出相应的程序框图及程序。

1.2基本算法语句1.2.1输入语句、输出语句和赋值语句1 .在输入语句中，若同时输入多个变量，则变量之间的分隔符号是 【 】A.逗号B.空格C.分号D.顿号2 . 3a =4b =a=b b=a c=b b=a a=c b=a a=b a=cc=b b=aa b =b a =输出 ,a b以上程序输出的结果是 【 】A.3,4B. 4,4C.3,3D.4,33 请从下面具体的例子中说明几个基本的程序框和它们各自表示的功能，并把它填在相应的括号内.4. 设计一个算法，要求输入一个圆的半径，便能输出该圆的周长和面积(π 取3.14)。

第一章算法初步第1课时算法与程序框图【知识梳理】1．算法的概念算法具有确定性、有效性、有限性等特征．算法设计与一般意义上的解决问题不同，它是对一类问题的一般解法的抽象与概括，主要借助一般的问题解决方法，又要包括此类问题的所有情形．它往往是把问题的解决划分为若干个可执行的步骤，有时甚至是重复多次，但最终都必须在有限个步骤之内完成．（1）用数学语言描述算法解决问题的过程大体可分为三步：第一步，明确问题的性质，分析题意．我们将问题简单地分为数值问题和非数值问题，不同类型的问题可以有针对性地采用不同的方法进行处理．第二步，建立问题的描述模型．对于数值型问题，可以建立数学模型，通过数学语言来描述问题．对于非数值型问题，我们可以建立过程模型，通过过程模型来描述问题．第三步，设计、确立算法．对于数值型问题，我们可以采用数值分析的方法进行处理，数值分析中有许多现成的固定算法，我们可以直接使用．当然我们也可以根据问题的实际情况设计算法．对于非数值型问题，根据过程模型分析算法并进行处理，也可以选择一些成熟的办法进行处理，如排序、递推等．（2）算法设计应注意：①与解决问题的一般方法有联系，从中提炼出算法；②将解决问题的过程分为若干个可执行步骤；③引入有关的参数或变量对算法步骤加以表达；④用最简练的语言将各个步骤表达出来；⑤算法的执行要在有限步内完成．2．程序框图程序框图又称流程图，是一种用___________、___________及___________来表示算法的图形．程序框图是人们用来描述算法步骤的形象化的方法．在程序框图中，一个或几个程序框的组合表示算法中的一个步骤；带有方向箭头的流程线将程序框连接起来，表示算法步骤的执行顺序．另外，程序框内还要有必要的文字说明．构成程序框图的图形符号、名称及其功能如下表：说明：一个完整的程序框图一定会包含终端框（用于表示一个算法的开始和结束），处理框（赋值、计算，算法中处理数据需要的算式、公式等）和流程线．3．算法的三种基本逻辑结构通常一个算法只能由三种基本逻辑结构构成，这三种基本逻辑结构分别是：顺序结构、条件结构和循环结构．（1）顺序结构顺序结构是由若干个___________的步骤组成的．这是任何一个算法都离不开的基本结构．顺序结构可以用程序框图表示为顺序结构是最简单的算法结构，语句与语句之间，框与框之间是按从上到下的顺序进行的，其中A和B两个框是依次执行的，只有在执行完A框所指定的操作后，才能接着执行B框所指定的操作，顺序结构各步骤之间不能随便调换，调换后可能会使算法不能运行或错误．（2）条件结构在一个算法中，经常会遇到一些条件的判断，算法的流程根据___________有不同的流向．条件结构就是处理这种过程的结构．条件结构对应的程序框图如图所示：（1）（2）注意：①无论条件是否成立，图（1）中只能执行“步骤A”框或“步骤B”框，但不可以既执行“步骤A”又执行“步骤B”，也不可以“步骤A”和“步骤B”都不执行；“步骤A”和“步骤B”中可以有一个是空的，如图（2）所示．②在利用条件结构画程序框图时，必须清楚判断的条件是什么，条件判断后分别对应着什么样的结果．（3）循环结构在一些算法中，要求___________同一操作的结构称为循环结构．即从算法某处开始，按照一定的条件反复执行某些步骤．反复执行的步骤称为循环体．循环结构有两种形式：直到型循环结构和当型循环结构．①直到型循环结构直到型循环结构可以用程序框图表示为：这个循环结构有如下特征：在执行了一次循环体后，对条件进行判断，如果条件不满足，就继续执行循环体，直到条件满足时终止循环．②当型循环结构当型循环结构可以用程序框图表示为：这个循环结构有如下特征：在每次执行循环体前，先对控制循环的条件进行判断，当条件满足时，执行循环体，否则终止循环．4．程序框图的画法在用自然语言表述一个算法后，可以画出程序框图，用顺序结构、条件结构和循环结构来表示这个算法．这样表示的算法清楚、简练，便于阅读和交流．设计一个算法的程序框图通常要经过以下步骤：第一步，用自然语言表述算法步骤.第二步，确定每一个算法步骤所包含的逻辑结构，并用相应的程序框图表示，得到该步骤的程序框图.第三步，将所有步骤的程序框图用流程线连接起来，并加上终端框，得到表示整个算法的程序框图.注意：流程线不要忘记画箭头，因为它是反映流程执行先后次序的，若不画出箭头，则难以判断各框的执行顺序．【参考答案】1.某一类问题；2.程序框流程线文字说明；3．（1）依次执行（2）条件是否成立（3）反复执行【重难点强化】1．算法的概念常见的设计算法的问题有解方程（组）问题、直接应用数学公式求解的问题、筛选问题、实际生活问题等，设计算法时要注意：（1）认真分析问题，联系解决此问题的一般数学方法；（2）综合考虑此类问题中可能涉及的各种情况；（3）将解决问题的过程划分为若干个步骤．【例1】已知直角三角形两直角边长为a，b，求斜边长c的一个算法分下列三步：①计算c=a，b的值；③输出斜边长c的值；其中正确的顺序是A．①②③B．②③①C．①③②D．②①③【答案】D【解析】由算法规则得：第一步：输入直角三角形两直角边长a，b的值，第二步：计算c第三步：输出斜边长c的值；这样，就是求斜边长c的一个算法．故选D．【点睛】算法是解决某一类问题的精确描述，这就要求我们在写算法时应简练、清晰，并善于分析任何可能出现的情况，体现出思维的严密性和完整性．【例2】下列关于算法的理解正确的是A．算法等同于解法B．任何问题都可以运用算法解决C．按照算法一步步执行，在有限步之后，总能得出结果D．解决某一个具体问题时，算法不同，结果也不同【答案】C2．顺序结构与顺序结构相关的问题一般是利用公式求解问题．在使用顺序结构书写程序框图时，（1）要注意各种框图符号的正确使用；（2）要先赋值，再运算，最后输出结果．【例3】将两个数a=2017，b=2018交换，使得a=2018，b=2017，下面语句正确一组是A．B．C．D．【答案】B【解析】先把b的值赋给中间变量c，这样c=2018，再把a的值赋给变量b，这样b=2017，把c的值赋给变量a，这样a=2018．故选B．【例4】已知函数f（x）=x2–3x+2，请设计一个算法，画出算法的程序框图，求f（3）+f（–1）的值．【点睛】画顺序结构的程序框图问题，不仅要遵循程序框图的画图原则，而且要看要求的量需要根据哪些条件求解，需要的条件必须先输入，或将已知的条件全部输入，求出未知的量．3．条件结构凡是需要先根据条件作出判断，然后再决定进行哪一个步骤的问题，在画程序框图时，必须引入判断框，采用条件结构，有时会需要多个判断框，至于判断框内的内容是没有固定顺序的．【例5】一算法的程序框图如图所示，若输出的12y=，则输入的x可能为A．–1 B．1 C．1或5 D．–1或1【答案】B【点睛】（1）对于求分段函数的函数值的程序框图画法：如果是分两段的函数，只需引入一个判断框；如果是分三段的函数，需要引入两个判断框；依此类推．至于判断框内的内容是没有顺序的．（2）判断框内的内容可以不唯一，但判断框内的内容一经改变，其相应的处理框等内容均要有所改变．【例6】阅读程序框图，如果输出的函数值在区间1142⎡⎤⎢⎥⎣⎦，内，则输入的实数x的取值范围是A．（–∞，–2] B．[–2，–1] C．[–1，2] D．[2，+∞）【答案】B【解析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算分段函数f（x）=[]()()222222x xx⎧∈-⎪⎨∈-∞-+∞⎪⎩，，，，，的函数值．又∵输出的函数值在区间1142⎡⎤⎢⎥⎣⎦，内，∴11242x<<，解得x∈[–2，–1]．故选B．4．循环结构如果算法问题中涉及的运算进行了许多次重复的操作，且先后参与运算的数之间有相同的变化规律，就可以引入变量(我们称之为循环变量)，构成循环结构．循环结构中常用的几个变量：①计数变量：即计数器，用来记录执行循环体的次数，如1n n=+．=+，1i i②累加变量：即累加器，用来计算数据之和，如S S i=+．③累乘变量：即累乘器，用来计算数据之积，如P P i=*．在程序框图中，一般要根据实际情况先给这些变量赋初始值．一般情况下，计数变量的初始值为1，累加变量的初始值为0，累乘变量的初始值为1．【例7】阅读如图的程序框图．若输入n=5，则输出k的值为A．2 B．3 C．4 D．5【答案】B【例8】已知流程图如图所示，该程序运行后，为使输出的b值为16，则循环体的判断框内①处应填A．2 B．3 C．4 D．5【答案】B【习题训练】1．早上从起床到出门需要洗脸刷牙（5 min）、刷水壶（2 min）、烧水（8 min）、泡面（3 min）、吃饭（10 min）、听广播（8 min）几个步骤，从下列选项中选出最好的一种算法A．第一步洗脸刷牙、第二步刷水壶、第三步烧水、第四步泡面、第五步吃饭、第六步听广播B．第一步刷水壶、第二步烧水同时洗脸刷牙、第三步泡面、第四步吃饭、第五步听广播C．第一步刷水壶、第二步烧水同时洗脸刷牙、第三步泡面、第四步吃饭同时听广播D．第一步吃饭同时听广播、第二步泡面、第三步烧水同时洗脸刷牙、第四步刷水壶2．我们已学过的算法有求解一元二次方程的求根公式，加减消元法求二元一次方程组的解，二分法求函数的零点等，对算法的描述有：①对一类问题都有效；②算法可执行步骤必须是有限的；③算法可以一步一步地进行，每一步都有确切的含义；④是一种通法，只要按部就班地做，总能得到结果．以上对算法的描述正确的有A．1个B．2个C．3个D．4个3．表示“根据给定条件判断”的符号是A B C D4．下面的程序框图是顺序结构的是5．如图所示的程序框图表示的算法意义是A．边长为3，4，5的直角三角形面积B．边长为3，4，5的直角三角形内切圆面积C．边长为3，4，5的直角三角形外接圆面积D．以3，4，5为弦的圆面积6．如图所示的程序框图是已知直角三角形两直角边a，b求斜边c的算法，其中正确的是7．根据所给的程序框图，如图所示，输出的结果是A ．3B ．1C ．2D ．08．下列说法：①条件结构是最简单的算法结构；②顺序结构就是按照程序语句运行的自然顺序，依次地执行顺序；③条件结构可以根据设定的条件，控制语句流程，有选择地执行不同的语句序列．其中正确的说法是 A ．①②B ．①③C ．②③D ．①②③9．求下列函数的函数值的算法中需要用到条件结构的是 A ．f （x ）＝x 2－1B ．f （x ）＝2x ＋1C ．f （x ）＝⎩⎪⎨⎪⎧x 2＋1x >1，x 2－1x ≤1.D ．f （x ）＝2x10．如右图所示的程序框图，其功能是A ．输入a ，b 的值，按从小到大的顺序输出它们的值B ．输入a ，b 的值，按从大到小的顺序输出它们的值C ．求a ，b 的最大值D ．求a ，b 的最小值 11．直到型循环结构对应的框图为12．如右图所示的程序框图中，循环体是A ．①B ．②C ．③D ．②③13．阅读如图框图，运行相应的程序，则输出i的值为A．3 B．4 C．5 D．6 14．下面程序框图表示的算法的运行结果是________．15．若R＝8，则如图所示的程序框图运行后的结果为a＝________．16．试写一个解三元一次方程组12,3316,2x y z x y z x y z ++=⎧⎪--=⎨⎪--=-⎩①②③的算法．17．已知半径为r 的圆的周长公式为C ＝2πr ，当r ＝10时，写出计算圆的周长的一个算法，并画出程序框图．18．如下算法：第一步，输入x 的值；第二步，若x ≥0，则y ＝x ；第三步，否则，y ＝x 2；第四步，输出y 的值， 若输出的y 值为9，则x 的值是 A ．3B ．－3C ．3或－3D ．－3或919．给出下列程序框图：若输出的结果为2，则①处的执行框内应填的是A ．x ＝2B ．b ＝2C ．x ＝1D ．a ＝520．下面的程序框图能判断任意输入的数的奇偶性．其中判断框中的条件是 A ．？B ．？C ．？D ．？x 0m =0x =1x =1m =21．某程序框图如图所示，现输入如下四个函数，则可以输出的函数是A ．()2f x x =B ．()1f x x=C ．()e x f x =D ．()3f x x x =+22．执行如图所示的程序框图，若输出的n ＝7，则输入的整数K 的最大值是A ．18B ．50C ．78D ．30623．执行如图所示的程序框图，输出的S 值为A ．1B ．23C ．1321D ．61098724．执行如图所示的程序框图，输出的结果为A．（－2，2）B．（－4，0）C．（－4，－4）D．（0，－8）25．执行如图所示的程序框图，输出的S值为A．1 B．3 C．7 D．1526．阅读如图所示的程序框图，运行相应的程序，输出的n的值为A．1 B．2 C．3 D．427．如图给出的是计算12＋14＋16＋18＋…＋1100的一个程序框图，其中判断框内应填入的条件是A ．i ＜50？B ．i ＞50?C ．i ＜25?D ．i ＞25?28．一个算法的程序框图如图所示，当输入的x 值为3时，输出y 的值恰好是13，则“①”处的关系式是A ．y ＝x 3B ．y ＝3－xC ．y ＝3xD ．y ＝x 1329．如图是求长方体的体积和表面积的一个程序框图，补充完整，横线处应填_____________．30．已知函数()()2log 2,22,x x y x x ⎧⎪=⎨-<⎪⎩图中表示的是给定x 的值，求其对应的函数值y 的程序框图．①处应填写_____________；②处应填写_____________．【习题训练答案】1.【答案】C2.【答案】D3.【答案】A4.【答案】A5.【答案】B6.【答案】C7.【答案】C8.【答案】C9.【答案】C 10.【答案】C 11.【答案】B 12.【答案】B 13.【答案】B 14.【答案】6 6【解析】由题意得P ＝5＋6＋72＝9，S ＝9×4×3×2＝63＝66．15.【答案】4【解析】由R ＝8得b ＝R2＝2，a ＝2b ＝4． 16.【答案】略． 17.【答案】详见解析．【解析】算法如下：第一步，令r ＝10．第二步，计算C ＝2πr ．第三步，输出C ． 程序框图如图：18.【答案】D 19.【答案】C 20.【答案】D 21.【答案】A 22.【答案】C 23.【答案】C 24.【答案】B 25.【答案】C 26.【答案】B 27.【答案】B 28.【答案】C【解析】当x ＝3时，∵x ＞0，由x ＝x －2，得x ＝1；再用x ＝x －2，得x ＝－1；而当x ＝－1时，3x ＝13． 29.【答案】【解析】根据题意，长方体的长、宽、高应从键盘输入，故横线处应填写输入框．30.【答案】2?x < 2log y x =【解析】框图中的①就是分段函数关系式两种形式的判断条件，故填写“2?x <”．②就是该函数的另一段表达式2log y x =．【点睛】求分段函数函数值的程序框图的画法：如果是分两段的函数，只需要引入一个判断框；如果是分三段的函数，需要引入两个判断框，依此类推，至于判断框内的内容是没有顺序的．第2课时算法与程序框图【知识梳理】1．五种基本算法语句任何一种程序设计语言中都包含五种基本的算法语句，分别它们是___________、___________、___________、___________、和___________．2．输入语句输入语句与程序框图中的___________对应，以BASIC语言为例，其一般格式为：INPUT “提示内容”；变量其中，“提示内容”一般是提示用户输入什么样的信息．输入语句的作用是输入提示内容要求的相应信息或值，计算机每次都把新输入的值赋给变量．3．输出语句输出语句与程序框图中的___________对应，以BASIC语言为例，其一般格式为：PRINT “S ”；S输出语句的作用是输出算法的信息(表达式)．输出语句的功能是在计算机的屏幕上输出常量、变量的值和系统信息．4．赋值语句赋值语句与程序框图中表示赋值的处理框对应，以BASIC语言为例，其一般格式为：___________赋值语句的作用是将表达式所代表的值赋给变量．判断赋值语句正确与否的两个步骤：（1）看格式，看是否满足“变量=表达式”的格式．（2）看内容，看赋值号是否超过了一个，即看是否进行了代数式的计算．5．条件语句条件语句与程序框图中的___________相对应．条件语句主要有两种，分别是“___________”语句和“___________”语句．（1）IF—THEN—END IF语句计算机在执行如图所示的条件语句时，首先对IF后的条件进行判断，如果(IF)条件符合，那么(THEN)执行语句体，否则执行END IF之后的语句．（2）IF—THEN—ELSE—END IF语句当计算机执行如图所示的条件语句时，首先对IF后的条件进行判断，如果(IF)条件符合，那么(THEN)执行语句体1，否则(ELSE)执行语句体2．学.科网注意：①当判断语句的两个出口只有一个需要执行其他语句时，使用“IF—THEN—END IF”语句；当判断语句的两个出口都需要执行其他语句时，使用“IF—THEN—ELSE—END IF”语句．②“条件”可以是复合条件，此时应用AND加以连接．③END IF是“出口”，是条件语句的结束符号，在书写程序时不要漏掉．6．循环语句循环语句与程序框图中的循环结构相对应．一般程序设计语言中都有__________和__________两种循环语句结构．（1）直到型(UNTIL)语句当计算机遇到UNTIL语句时，先执行一次DO和UNTIL之间的循环体，再对UNTIL后的条件进行判断．如果条件不符合，继续执行循环体；然后再检查上述条件，如果条件仍不符合，再次执行循环体，直到条件符合时为止．这时，计算机将不执行循环体，直接跳到UNTIL语句后，接着执行UNTIL语句之后的语句．如图所示：（2）当型(WHILE)语句当计算机遇到WHILE语句时，先判断条件的真假，如果条件符合，就执行WHILE和WEND之间的循环体；然后再检查上述条件，如果条件仍符合，再次执行循环体，这个过程反复进行，直到某一次条件不符合为止．这时，计算机将不执行循环体，直接跳到WEND语句后，接着执行WEND之后的语句．如图所示：学&科网应用循环语句编写程序时需注意：①循环语句中的循环变量一般要设初始值．②在循环过程中需要有“结束”的语句，程序中最忌“死循环”．【重难点强化】1．输入语句、输出语句、赋值语句（1）输入语句可以给多个变量赋值，其格式为：INPUT “提示内容1，提示内容2，提示内容3，…”；变量1，变量2，变量3，…（2）输出语句具有计算功能．（3）对于赋值语句，①在代数中A＝B与B＝A是等效的两个等式，而在赋值语句中则是两个不同的赋值过程．②“＝”左边必须是变量，右边可以是常量、变量或算式．③一个语句只能给一个变量赋值，不能对几个变量连续赋值，但可以辗转赋值．④可给一个变量多次赋值，但只保留最后一次所赋的值．【例1】下列语句正确的是①输入语句INPUT x ②输入语句INPUT “A，B，C”；a，b，c③输出语句PRINT A+B=C ④赋值语句3=A．A．①③B．②③C．②④D．①②【答案】D【解析】根据输入语句的一般格式知：①②正确；输出语句不具有赋值或执行功能，③错误；④赋值语句应改为A=3，④错误．故选D．学科*网【例2】下列程序语句正确的是A．输出语句PRINT A=4 B．输入语句INPUT x=3C．赋值语句A=A*A+A–3 D．赋值语句55=a【答案】C2．条件语句条件语句可实现算法中的条件结构，当计算机处理按条件判断后的不同情况时，就需要用到条件语句．如求分段函数的函数值等，往往要用到条件语句，有时甚至要用到条件语句的嵌套．在有些较为复杂的算法中，有时需要对按条件执行的某一语句(特别是ELSE后的语句)继续按照另一个要求进行判断，这时可以再利用一个条件语句进行判断，这就形成了条件语句的嵌套．条件语句的嵌套是条件结构嵌套的实现和表达．一般形式如下：IF 条件1 THEN语句体1ELS EIF 条件2 THEN语句体2ELSE语句体3END IFEND IF【例3】如图所示的程序是计算函数y=f（x）函数值的程序，若输入的x的值为4，则输出的y值为A．17 B．3 C．–3 D．–17【答案】C【例4】下列关于条件语句的叙述，正确的是A．条件语句中必须有if、else和end B．条件语句中可以没有endC．条件语句中可以没有else，但必须有end D．条件语句中可以没有else及没end【答案】C【解析】条件语句是处理条件分支逻辑结构的算法语句．表示形式有2种：①IF–THEN–ELSE格式：执行时，先对IF后的条件进行判断，若条件符合，执行语句1，否则执行语句2．②IF–THEN格式：执行时，先对IF后的条件进行判断，若条件符合，执行THEN后的语句，否则结束条件语句，执行其他语句．所以条件语句中可以没有else，但必须有end．故选C．3．循环语句WHILE语句与UNTIL语句两种循环语句的联系与区别：（1）联系：两种语句都可以实现计算机反复执行循环体的目的，只是表达形式不同．一般来讲，WHILE 语句与UNTIL语句可以相互转化．（2）区别：①直到型循环语句是先执行（循环体），后判断（条件），而当型循环语句是先判断（条件），后执行（循环体）．②直到型循环语句是条件不满足时执行循环体，条件满足时结束循环；而当型循环语句是当条件满足时执行循环体，不满足时结束循环．③直到型循环结构至少执行一次循环体，而当型循环结构可能一次也不执行循环体．④在设计程序时，一般说来，这两种语句用哪一种都可以，但在某种限定条件下，有时用WHILE语句较好，有时用UNTIL语句较好．【例5】执行下列程序后，输出的i的值是A．5 B．6 C．10 D．11【答案】D4．混淆WHILE 语句与UNTIL 语句【例6】编写程序计算98246++⋅⋅⋅++的值． 【解析】【错解一】程序如下：【错解二】程序如下：【分析】错解一中WEND 应与WHILE 对应；错解二中DO 与LOOP UNTIL 对应，另外，i=i+1应为i=i+2． 【正解一】程序如下：【正解二】程序如下：【习题训练】1．对赋值语句的描述正确的是①可以给变量提供初值；②可以将表达式的值赋给变量；③可以给一个变量重复赋值；④不能给同一个变量重复赋值．A．①②③B．①②C．②③④D．①②④2．执行‘PRINT “3+5=”；3+5’的输出结果是A．3+5=3+5 B．3+5=8 C．8=3+5 D．8=83．下列程序的输出结果是A．10 B．15 C．25 D．54．阅读下面的程序，判断程序执行后的结果是A．6，9 B．9，6 C．6，12 D．9，95．在设计求函数2,2()1,2266,2x xf x x xx x⎧>⎪=--<≤⎨⎪-≤-⎩的值的程序中不可能用到的算法语句为A．输入语句B．条件语句C．输出语句D．循环语句6．根据下列算法语句，当输入x为60时，输出y的值为A．25 B．30 C．31D．617．读下面的程序：该程序的作用是A．计算9个数的和B．计算9个数的平均数C．计算10个数的和D．计算10个数的平均数8．以下程序运行后的输出结果为i=1WHILE i<8i=i+2S=2*i+3i=i–1WENDPRINT SENDA．17 B．19 C．21 D．239．下列给出的输入、输出语句正确的是①输入语句：INPUT a；b；c ②输入语句：INPUT x=3③输出语句：PRINT A=4 ④输出语句：PRINT 20，3*2A．①②B．②③C．③④D．④10．执行图程序中，若输出y的值为2，则输入x的值为__________．11．下面是用程序语句表示的一个问题的算法，试根据其画出程序框图．12．下列正确的语句的个数是①输入语句：INPUT a+2 ②赋值语句：x=x–5 ③输出语句：PRINT M=2A．0 B．1 C．2 D．313．阅读下面的程序，然后判断程序执行后的结果是A．5 B．15 C．11 D．14 14．若下面的程序运行之后输出的值为16，那么输入的值x应该是A．3或3-B．5-C．5或3-D．5或5-15．阅读下面的程序：程序运行的结果是A．3B．3 4C．3 4 5D．3 4 5 616．下面为一个求50A．i>50 B．i<50 C．i>=50 D．i<=50 17．如图程序的输出结果为__________181920．下列程序运行的结果是【习题训练答案】17．【答案】（7，10）18．【答案】4，1 19．【答案】7 20．【答案】64。

高二数学算法与框图试题答案及解析1.设，，c，则（）A．B．C．D．【答案】B【解析】故选B2.看下面的伪代码，最终输出的结果是（）S←0For I from 1 to 100 step 2S←S+I2End forPrint SA．1+2+3+…+100B．12+22+32+…+1002C．1+3+5+…+99D．12+32+52+…+992【答案】D【解析】根据语句“For I from 1to 100step 2”得到I的取值，然后根据循环体可值所求结果．解：∵For I from 1 to 100 step 2∴I的取值为1，3，5，…，99∵S←0，S←S+I2∴最终输出的结果是12+32+52+ (992)故选D．点评：本题主要考查了循环语句，解题的关键是弄清I的取值可能，属于基础题．3.计算机是将信息转换成二进制数进行处理的，二进制即“逢二进一”，如：表示二进制的数，将它转换成二进制的形式是，那么将二进制数转换成十进制的形式是（）A．B．C．D．【答案】 C【解析】解．考点；二进制、十进制之间的转化．点评：本题考查的知识点是二进制、十进制之间的转化．4.下面是一个算法的伪代码，输出结果是．【答案】14【解析】第一次循环：;第二次循环：;第三次循环：;结束循环，输出【考点】循环结构流程图3，则输出y的值为（）5.执行如图所示的程序框图，若输入x的值为2+log2A．B．C．D．【答案】【解析】程序框图执行过程中的数据变化如下：【考点】程序框图的应用6.若所给的程序运行结果为，那么判断框中应填入的关于的条件是A．?B．C．D．?【答案】D【解析】模拟算法：满足条件；满足条件；不满足条件，输出，故判断框中应填?，选D．【考点】程序框图．7.执行如图所示程序框图（算法流程图），输出的结果是A．5B．6C．7D．8【答案】C【解析】模拟算法：是的倍数；,,不成立；不是的倍数，，，不成立；是的倍数，，，不成立；不是的倍数，，，不成立;是的倍数，，，不成立;不是的倍数，，，成立，输出，故选C．【考点】程序框图．8.用辗转相除法求与的最大公约数时，需做的除法次数为A．3B．4C．5D．6【答案】A【解析】因为,所以共做3次除法运算可求两个数的最大公约数，故选A．【考点】算法案例．9.程序框图中表示计算的是（）A．B．C．D．【答案】A【解析】A中执行框可表示计算；B中为输入输出框；C中为判断框；D中为起止框【考点】程序框图10.如图所示,程序框图（算法流程图）的输出结果是（）A．B．C．D．【答案】B【解析】第一次循环可得：，满足条件继续循环；第二次循环可得：，满足条件继续循环；第三次循环可得：，不满足条件，跳出循环体，可得，故选择【考点】流程图11.某程序框图如图所示，若输出的S＝57，则判断框内为（）A．k＞4?B．k＞5?C．k＞6?D．k＞7?【答案】A【解析】，此时输出，所以判断框内应为k＞4?．【考点】1．程序框图；12.设计程序框图计算12＋22＋32＋…＋10002，并写出程序．【答案】【解析】本题属于程序框图和程序语句的书写，是常见的一种框图，在书写的过程中注意判断框中的判定条件是什么，以及用哪一种循环结构．试题解析：【考点】1．程序框图；2．程序语句；13.下边程序执行后输出的结果是（）。

算法与程序框图练习题1．下列关于程序框图的描述①对于一个算法来说程序框图是唯一的；②任何一个框图都必须有起止框；③程序框图只有一个入口，也只有一个出口；④输出框一定要在终止框前．其中正确的有()A．1个B．2个C．3个D．4个答案 B解析②、③正确，对于一个算法来说，程序框图不唯一，与设计有关，故①错．输入输出的位置，不一定在开始和结束处，故④错．2．某程序框图如图所示，该程序运行后输出的k的值是()A．4 B．5 C．6 D．7答案 A解析当k＝0时，S＝0S＝1k＝1，当S＝1时，S＝1＋21＝3k＝2，当S＝3时，S＝3＋23＝11<100k＝3，当S＝11时，k＝4，S＝11＋211>100，故k＝4.3．(2010年高考天津卷)阅读右边的程序框图，运行相应的程序，则输出s的值为()A．－1B．0C．1 D．3解析：选B.当i＝1时，s＝1×(3－1)＋1＝3；当i＝2时，s＝3×(3－2)＋1＝4；当i＝3时，s＝4×(3－3)＋1＝1；当i＝4时，s＝1×(3－4)＋1＝0；紧接着i＝5，满足条件i>4，跳出循环，输出s的值为0.4．如下图是一个算法的程序框图，该算法所输出的结果是( )A.12B.23C.34D.45 答案 C解析 运行第一次的结果为n ＝0＋11×2＝12；第二次n ＝12＋12×3＝23；第三次n ＝23＋13×4＝34.此时i ＝4程序终止， 即输出n ＝34.5．(2010年高考浙江卷)某程序框图如图所示，若输出的S ＝57，则判断框内为( )A ．k >4?B ．k >5?C ．k >6?D ．k >7? 解析：选A.当k ＝1时，k ＝k ＋1＝2，S ＝2×1＋2＝4； 当k ＝2时，k ＝k ＋1＝3，S ＝2×4＋3＝11； 当k ＝3时，k＝k＋1＝4，S＝2×11＋4＝26；当k＝4时，k＝k＋1＝5，S＝2×26＋5＝57.此时S＝57，循环结束，k＝5，所以判断框中应为“k>4？”．6．阅读下边的程序框图，若输出s的值为－7，则判断框内可填写()A．i<3? B．i<4?C．i<5? D．i<6?答案 D解析i＝1，s＝2；s＝2－1＝1，i＝1＋2＝3；s＝1－3＝－2，i＝3＋2＝5；s＝－2－5＝－7，i＝5＋2＝7.因输出s的值为－7，循环终止，故判断框内应填“i<6？”．7．下列程序框图表示的算法是()A．输出c，b，a B．输出最大值C．输出最小值D．比较a，b，c的大小答案 B解析根据程序框图可知，此图应表示求三个数中的最大数．8．(2010年高考陕西卷)右图是求x1，x2，…，x10的乘积S的程序框图，图中空白框中应填入的内容为( )A ．S ＝S *(n ＋1)B ．S ＝S *x n ＋1C ．S ＝S *nD ．S ＝S *x n解析：选D.由循环结构的程序框图知识可知选D.9．阅读如图所示的程序框图，运行相应的程序，则输出的i 值等于( )A ．2B ．3C ．4D ．5 答案 CS=0→i ＝1→a ＝2 →S ＝2→i ＝2→a ＝8 →S ＝10→i ＝3→a ＝24 →S ＝34→i ＝4→输出i ＝4. 二、填空题10．如图所示的程序框图，输出的结果是S ＝7，则输入的A 值为________．解析：该程序框图的功能是输入A ，计算2A ＋1的值．由2A ＋1＝7，解得A ＝3. 答案：311．求边长为3,4,5的直角三角形的内切圆半径的算法为： 第一步 输入__________________； 第二步 计算r ＝a ＋b －c2；第三步 输出r .答案 a ＝3，b ＝4，c ＝512．根据下面的程序框图操作，使得当成绩不低于60分时，输出“及格”，当成绩低于60分时，输出“不及格”，则框1中填________，框2中填________．答案 是 否解析 由x ≥60与及格对应知1处填是，则2处填否．13．如图，是求实数x 的绝对值的算法程序框图，则判断框①中可填________．解析：由于|x |＝⎩⎪⎨⎪⎧x ， x ≥0－x ，x <0，或|x |＝⎩⎪⎨⎪⎧x ， x >0－x ，x ≤0，故根据所给的程序框图，易知可填x >0或x ≥0.答案：x >0或x ≥014．在如图的程序框图中，输出结果是________．解析：a ＝5时，S ＝1＋5＝6； a ＝4时，S ＝6＋4＝10；a ＝3时，终止循环，输出S ＝10. 答案：1015．已知下列框图，若a ＝5，则输出b ＝________.答案 26解析 因a ＝5，所以5>5不成立， 判断框执行“否”，即b ＝52＋1＝26.16．执行如图所示的程序框图，若输入x ＝4，则输出y 的值为________．答案 －54解析 当输入x ＝4时，计算y ＝12x －1，得y ＝1.不满足|y －x |<1.于是得x ＝1，此时y ＝12－1＝－12，不满足|－12－1|<1，此时x ＝－12，又推得y ＝－54.这样|y －x |＝|－54＋12|＝34<1，执行“是”，所以输出的是－54.。

高一数学算法与框图试题答案及解析1.把89化成五进制数的末位数字为（）A．1B．2C．3D．4【答案】D【解析】，故，所以89化成五进制数的末位数字为4.【考点】带余除法.2.下列对算法的理解不正确的是（）A．一个算法包含的步骤是有限的B．一个算法中每一步都是明确可操作的，而不是模棱两可的C．算法在执行后，结果应是明确的D．一个问题只可以有一个算法【答案】D【解析】算法的特征：确定性、有限性、可行性；算法是解决一类问题的，所以D错误.考点:算法的概念及特征.3.任何一个算法都必须有的基本结构是（）．A．顺序结构B．条件结构C．循环结构D．三个都有【答案】A【解析】在执行过程中，如果不需要分类讨论就没有条件结构，如果不需要重复执行某些操作，就不需要循环结构，但顺序结构一定有【考点】算法的三种结构4.在右图的算法中，如果输入A=138，B=22，则输出的结果是（）A．138B．2C．4D．0【答案】B【解析】程序执行过程中数据变化如下,输出2【考点】程序框图5.如图所示程序框图中，输出（）A．B．C．D．【答案】D【解析】由程序框图值，第一次运行；第二次运行；第三次运行；…指导满足条件，运行终止，此时，，故选D．【考点】程序框图6.当时，执行如右图所示的程序框图，输出的值为（）A．30B．14C．8D．6【答案】B【解析】当时，，是，进入循环,时，，是，进入循环,时，，是，进入循环,时，，否，所以退出循环，所以．【考点】1．程序框图的应用；2循环结构．7.阅读下图程序框图,运行相应的程序,则程序运行后输出的结果为（）A．7B．9C．11D．13【答案】B【解析】首先进入程序，时，，否，所以进入，时，，否，此时，，否，，，否，，，是，所以对称循环，此时输出．【考点】1．循环结构；2．程序框图的应用．8.运行下图所示的程序，如果输出结果为sum＝1320，那么判断框中应填（）A．i≥9B．i≥10C．i≤9D．i≤10【答案】B【解析】此程序框图是求从12开始的，递减的正整数的成绩，因为输出的是，而，所以只有3次进入循环结构，那么判定框应填入【考点】1．程序框图的应用；2．条件结构；3．循环结构．9.某班有24名男生和26名女生，数据，…是该班50名学生在一次数学学业水平模拟考试中的成绩（成绩不为0），如图所示的程序用来同时统计全班成绩的平均数：，男生平均分：，女生平均分：．为了便于区别性别，输入时，男生的成绩用正数，女生的成绩用其相反数，那么在图中空白的判断框和处理框中，应分别填入（）A．B．C．D．【答案】D【解析】根据题意男生平均分用变量表示，女生平均分用变量表示，可得满足条件1时，表示该分数为男生分数，又由男生的成绩用正数，故条件1为，统计结束后，为正数，为负数（女生成绩和的相反数），故此时，故选D。

高中数学《算法与框图》练习题（含答案解析）一、单选题1．执行如图所示的程序框图，若输入的10N=，则输出的X=（）A．132B．121C．119D．1172．按如图所示的算法框图运算，若输入x=3，则输出k的值是（）A．3B．4C．5D．63．运行如图所示的程序框图，若输入的A，B的值分别为5，7，则输出的结果为（）A．5，7B．7，5C．7，7D．5，54．用辗转相除法求得288与123的最大公约数是（）A．42B．39C．13D．35．流程图中表示判断框的是（）．A．矩形框B．菱形框C．圆形框D．椭圆形框6．给出如图所示的程序框图，若输入x的值为52-，则输出的y的值是（）A．－3B．－1C．－2D．07．执行如图所示的程序框图，如果输入的x，Ry∈，那么输出的S的最大值为（）A ．0B ．1C ．2D ．48．“大衍数列”来源于《乾坤谱》中对《易传》“大衍之数五十”的推论，主要用于解释中华传统文化中的太极衍生原理，数列中的每一项，都代表太极衍生过程中，曾经经历过的两仪数量总和，是中华传统文化中隐藏着的世界数学史上第一道数列题.如图是求“大衍数列”前n 项和的程序框图.执行该程序框图，输入6m =，则输出的S =（ ）A ．18B ．26C ．44D ．689．某同学为了求2222123n ++++，设计了如图所示的程序框图，在该程序框图中，①和①两处应分别填入（ ）A ．2,S S i i n =+≥B ．2(1),1S S i i n =+-≥+C ．2,S S i i n =+>D ．2(1),1S S i i n =++≥-10．如图所示的形状出现在南宋数学家杨辉所著的《详解九章算法》中，后人称为“三角垛”．“三角垛”最上层有1个球，第二层有3个球，第三层有6个球，…．如图所示的程序框图，输出的S 即为小球总数，则S =（ ）A ．35B ．56C ．84D ．120二、填空题11．运行如图所示的伪代码，输出的T 的值为________.12．用秦九韶算法求函数432()2321f x x x x x =-+++，当1x =时的值时，2=v ___________．13．执行如图所示的程序框图，若输出的结果为48，则输入k 的值可以为______.14．设2134与1455的最大公约数为m ，则m 化为三进制为__________.三、解答题15．（1）求98的二进制数（2）用辗转相除法求840与1764的最大公约数（3）用秦九韶算法计算函数()432354f x x x x =++-当3x =时的函数值.16．某学校行政机构关系如下：①校长下设两名副校长和校长办公室；①两名副校长又各自管理教务处、教科室和保卫科、政教处、总务处；①各科室共同管理和服务各班级．试画出该校的行政组织结构图．17．任意给定一个正实数，设计一个算法求以这个数为半径的圆的面积.18．用二分法设计一个求方程230x -=在[]1,2上的近似根的算法.（近似根与精确解的差的绝对值不超过0.0005）参考答案与解析：1．B【分析】根据程序循环体内的执行逻辑，依次列出每步的执行结果直到n N ≥，确定输出结果N 即可.【详解】由程序的执行逻辑知：输入10N =，1、1,1X n ==：得1,23X n ==，n N <，执行循环体； 2、13X =，2n =：得1,35X n ==，n N <，执行循环体； 3、15X =，3n =：得1,47X n ==，n N <，执行循环体； 4、17X =，4n =：得1,59X n ==，n N <，执行循环体； …10、119X =，10n =：得121X =，11n N =>，跳出循环体． 输出121X =． 故答案为：B.2．B【分析】根据程序框图依次进行计算即可【详解】当1k =时，1312x =-=；当2k =时，2213x =-=；当3k =时，33126x =-=；当4k =时，42612021x =->，故输出的4k =，故选：B3．B【分析】按照程序框图运行即可.【详解】模拟程序的运行，可得：5A =，7B =，满足A B <，5K =，则7A =，5B =．所以输出A ，B 的值分别为7，5．故选: B ．4．D【分析】根据辗转相除法的步骤，将288和133带入进行运算，即可得到答案.【详解】288212342=⨯+12324239=⨯+42393=+39133=⨯故288与123的最大公约数是3故选：D.5．B【分析】根据算法框图中表示判断的是菱形框，即可得出答案.【详解】解：流程图中矩形框表示处理框，菱形框表示判断框，圆形框表示起止框，没有椭圆形框，所以B 选项正确.故选：B【点睛】本题考查流程图中图形符号含义，属于基础题.6．C【分析】模拟执行程序，即可求出输出值； 【详解】解：输入52x =-，则55221222-⎛⎫=> ⎪⎝⎭，满足12?2x ⎛⎫> ⎪⎝⎭， 第二次循环，51222x =-+=-，则11221222-⎛⎫=< ⎪⎝⎭，不满足12?2x ⎛⎫> ⎪⎝⎭，则22222211log log log 22log 2224y -⎛⎫=-===-=- ⎪⎝⎭，输出2-； 故选：C7．D【分析】画出判断条件对应的不等式组所表示的平面区域，结合图形，确定目标函数的最优解，利用程序框图的输出结果，即可求解.【详解】由题意，不等式组002x y x y ≥⎧⎪≥⎨⎪+≤⎩所表示的平面区域，如图所示，目标函数2S x y =+，可化为直线2y x S =-+，当直线2y x S =-+经过点A 时，直线在y 轴上的截距最大，此时目标函数取得最大值，又由02y x y =⎧⎨+=⎩，解得(2,0)A ，所以目标函数的最大值为max 4S ，又由不等式002x y x y <⎧⎪<⎨⎪+<⎩时，根据程序框图，可得1S =，所以输出的S 的最大值为4.故选：D.8．C【分析】根据程序流程图，代入6m =，计算出结果即可.【详解】①6m =，1n =，2102n a -==，0S S a =+=，此时n m <； ①2n =，222n a ==，2S S a =+=，此时n m <； ①3n =，2142n a -==，6S S a =+=，此时n m <； ①4n =，282n a ==，14S S a =+=，此时n m <； ①5n =，21122n a -==，26S S a =+=，此时n m <； ①6n =，2182n a ==，44S S a =+=，此时n m ≥， 结束程序，输出结果为44，故选：C9．C【分析】根据流程图及最后输出的结果逐项判断后可得正确的选项.【详解】对于A ，第1次判断前21,2S i ==，第2次判断前2212,3S i =+=，依次，最后一次判断前，()222121S n =+++-，此时i n =，终止循环， 故此时输出()222121S n =+++-，不合题意.对于C ，第1次判断前21,2S i ==，第2次判断前2212,3S i =+=，依次，最后一次判断前，22212S n =+++，此时1i n =+，终止循环， 故符合题意.对于B ，第1次判断前20,2S i ==，第2次判断前21,3S i ==，依次，最后一次判断前，()222121S n =+++-，此时1i n =+，终止循环， 故此时输出()222121S n =+++-，不合题意.对于D ，第1次判断前22,2S i ==，第2次判断前2223,3S i =+=，依次，最后一次判断前，()222231S n =+++-，此时1i n =-，终止循环， 故此时输出()222231S n =+++-，不合题意.故选：C10．B【分析】设第n 层小球个数为n a ，根据程序框图可知，输出的123456S a a a a a a =+++++，求出各个数即可得到.【详解】设第n 层小球个数为n a ，由题意可知，1n n a a n --=()2n ≥.根据程序框图可知，输出的123456S a a a a a a =+++++，又11a =，23a =，36a =，43410a a =+=，54515a a =+=，65621a a =+=，所以136********S =+++++=.故选：B.11．16【分析】模拟程序的运行过程，即可得出程序运行后的输出结果.【详解】当1T =时，3i =；当134T =+=时，5i =；当459T =+=时，7i =；当9716T =+=时，98i =>.所以输出16T =.故答案为：16.【点睛】本题主要考查了程序语言的应用问题，模拟程序的运行过程是常用的方法，属于基础题. 12．0【分析】利用秦九韶算法的定义计算即可.【详解】012221311110v v v ==⨯-=-=-⨯+=，，故答案为: 013．8（答案不唯一）【分析】根据程序框图依次计算，直至推出48s =截止，判断条件.【详解】执行程序框图，可知：第一次循环：n ＝1＋3＝4，S ＝2×1＋4＝6；第二次循环：n ＝4＋3＝7，S ＝2×6＋7＝19；第三次循环：n ＝7＋3＝10，S ＝2×19＋10＝48，要使得输出的结果为48，可知k 可以为8.故答案为：8（答案不唯一）14．()310121【分析】先求出2134与1455的最大公约数97m =，再利用“辗转相除法”进位方法，即可得出结果.【详解】解：21341455679,1455679297,679977=+=⨯+=⨯，2134∴与1455的最大公约数为97，97m ∴=，用97连续除3得余数，可得：97化为三进制数=()310121.故答案为：()310121.15．（1）()21100010（2）84（3）254【解析】（1）将98写成的幂的和的形式，即可找到98的二进制数；（2）根据辗转相除法的规则，即可求出最大公约数；（3）先将()f x 写成(){}23054x x x x +++-⎡⎤⎣⎦的形式，再计算3x =时01234,,,,v v v v v 的值即可.【详解】（1）6598222=++，所以98的二进制数是()21100010.（2）1764284084=⨯+，8401084=⨯，所以840与1764的最大公约数为84.（3）()(){}23054f x x x x x =+++-⎡⎤⎣⎦.0 3.v =12339.v =⨯+=293027.v =⨯+=3273586.v =⨯+=48634254.v =⨯-=【点睛】本题考查二进制，辗转相除法，秦九昭算法等知识，属于基础题.16．见解析【分析】根据题目中的条件，找出各要素之间的关系，校长只负责两名副校长和校长办公室，所以校长下只有两名副校长和校长办公室，依次类推，两名副校长又各自管理教务处、教科室和保卫科、政教处、总务处；班级由所有的科室负责.【详解】该校的行政组织结构图如图所示：【点睛】本题考查组织结构图的画法，关键是找出各要素之间的关系， 属于基础题.17．见解析【分析】由算法的概念可知：算法是先后顺序的，结果明确性，每一步操作明确的，根据已知半径求圆的面积的算法的先后顺序，即可得出结果.【详解】第一步：输入任意正实数r ；第二步：计算2S r π=；第三步：输出圆的面积S【点睛】本题考查算法的概念，解题关键是算法步骤的排序和格式，属于基础题.18．见解析【分析】计算(1)0,(2)0f f <>，设121,2x x ==，122x x m +=，判断()f m 的符号，根据零点存在定理得到算法.【详解】第一步：令2()3f x x =-，(1)20,(2)10f f =-<=>，∴设121,2x x ==；第二步：令122x x m +=，判断()f m 是否为0，若是，则m 为所求；若不是，则继续判断()1()f x f m ⋅大于0还是小于0； 第三步：若()1()0f x f m ⋅>，则令1x m =；否则，令2x m =；第四步：判断120.0005x x-≤是否成立？若是，则12,x x之间的任意值均为满足条件的近似根；若不是，则返回第二步.【点睛】本题考查了求方程近似根的算法，意在考查学生对于算法的理解和应用。

高三数学算法和程序框图试题1.运行如图所示的程序框图，则输出的运算结果是_____________【答案】【解析】因为第一次进入循环，运算后S＝，i＝1＜4第二次进入循环，运算后S＝，i＝2＜4第三次进入循环，运算后S＝，i＝3＜4第四次进入循环，运算后S＝，i＝4≥4跳出循环输出S＝.【考点】算法，框图，数列求和，裂项法.2.如图所示，程序框图（算法流程图）的输出结果是（）A．34B．55C．78D．89【答案】B【解析】由题意，①②③④⑤⑥⑦⑧，从而输出，故选B.【考点】1.程序框图的应用.3.执行右侧的程序框图，若输入，则输出 .【答案】C【解析】第一次运行后y=5，第二次运行后y=，第三次运行后，此时，满足条件，故输出.【考点】程序框图.4.定义某种运算，运算原理如下图所示，则式子的值为。

【答案】13【解析】解：=所以答案应填13.【考点】1、新定义；2、指数运算与对数运算.5.某程序框图如图所示，若使输出的结果不大于20，则输入的整数的最大值为（）A．3B．4C．5D．6【答案】B【解析】这是一个循环结构，循环的结果依次为：.再循环一次，S的值就大于20，故的值最大为4.【考点】程序框图.6. [2013·湖北高考]阅读如图所示的程序框图，运行相应的程序．若输入m的值为2，则输出的结果i＝________.【答案】4【解析】i＝1，A＝2，B＝1→i＝2，A＝4，B＝2→i＝3，A＝8，B＝6→i＝4，A＝16，B＝24，输出i＝4.7.已知某程序框图如图所示，则该程序运行后输出的结果为（ )A．B．C．D．【答案】A【解析】运行第一次：成立；运行第二次：成立；运行第三次：成立；运行第四次成立；运行第五次：成立；运行第2007次：成立；运行第2008次：不成立；输出A的值：故选A.【考点】循环结构.8.如果执行如图的程序框图，那么输出的值是__________．【答案】【解析】依题意可得程序框图是一个以6为周期的数列，输出的S分别是由2014除以6的余数为4.所以输出的值是.【考点】1.程序框图.2.周期数列.9.执行如图所示的算法框图，输出的结果是，则判断框内应填入的条件是（）A．B．C．D．【答案】A【解析】本程序计算是，因为，由，解得，此时，不满足条件，所以选A.【考点】程序框图.10.阅读如图所示的程序框图，若输入，则输出的值为__________.【答案】.【解析】第一次循环，，不成立；执行第二次循环，，，不成立；执行第三次循环，，，不成立；执行第四次循环，，，成立，跳出循环体，输出的值为.【考点】算法与程序框图11.一个算法的程序框图如右图所示，若该程序输出的P位于区间内，则判断框内应填入的条件是（）A．B．C．D．【答案】C【解析】因为第一次循环，第二次循环，第三次循环，第四次循环，第五次循环，第六次循环，此时应结束循环，所以判断框中应填选C.【考点】循环结构流程图12.A．B．C．D．【答案】C【解析】程序执行过程中，的值依次为；；；；；，程序结束，输出．【考点】程序框图.13.执行如图所示的程序框图，输出的所有值之和是_________.【答案】【解析】由程序框图可知，当时，1不是3的倍数，输出1；当，3是3的倍数，不输出；同理，接下来输出的数还有，所以之和是.【考点】程序框图的应用.14.执行下图的程序框图，如果输入，则输出的值为．【答案】【解析】由题意，．【考点】程序框图．15.某程序框图如图所示，则该程序运行后输出的值为．【答案】7【解析】开始时，，进入循环，；，继续循环，；，继续循环，；，跳出循环，故.【考点】1、程序框图的循环结构；2、数列的列项求和.16.执行如图所示的程序框图，输出的S＝________．【答案】【解析】执行第一次循环时S＝，i＝1；第二次循环S＝，i＝2，此时退出循环．故输出S＝.17.执行程序框图，则输出的S是（）A．5040B．4850C．2450D．2550【答案】C【解析】由程序框图分析可知：第一次循环：第二次循环：第三次循环：…，当时循环结束，此时，故输出的结果为2450，选C.【考点】1.程序框图；2.等差数列的前n项和公式.18.执行如图所示的程序框图,则输出的k的值是()A．3B．4C．5D．6【答案】C【解析】依次执行循环体得s=1,k=2;s=2,k=3;s=6,k=4;s=15,k=5,s=31,满足s>15,输出k=5.故选C.19.如果执行如图的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则()A．A+B为a1,a2,…,aN的和B．为a1,a2,…,aN的算术平均数C．A和B分别是a1,a2,…,aN中最大的数和最小的数D．A和B分别是a1,a2,…,aN中最小的数和最大的数【答案】C【解析】随着k的取值不同,x可以取遍实数a1,a2,…,aN,依次与A,B比较,A始终取较大的那个数,B始终取较小的那个数,直到比较完为止,故最终输出的A,B分别是这N个数中的最大数与最小数. 20.如图是一个算法流程图，则输出的k的值是________．【答案】6【解析】根据程序框图可知，k＝1时，12－1×6＋5≤0；k＝2时，22－2×6＋5≤0；k＝3时，32－3×6＋5≤0；k＝4时，42－4×6＋5≤0；k＝5时，52－5×6＋5≤0；k＝6时，62－6×6＋5＞0.故输出的k的值是6.21.运行如图的程序框图，若输出的结果是，则判断框中可填入A．B．C．D．【答案】B【解析】程序的运算功能是，而，因此.【考点】程序框图.22.执行下面的程序框图，若输入的ε的值为0.25，则输出的n的值为________．【答案】3【解析】逐次计算的结果是F1＝3，F＝2，n＝2；F1＝5，F＝3，n＝3，此时输出，故输出结果为3.23.阅读如图所示的程序框图，若运行相应的程序，则输出的S的值是() A．102B．21C．81D．39【答案】A【解析】S＝1×31＋2×32＋3×33＝10224.一个算法的程序框图如图，则其输出结果是（）A．0B．C．D．【答案】B【解析】由题意可知：.【考点】1.程序框图；2.三角函数的周期性.25.阅读程序框图，运行相应的程序，当输入x的值为-25时，输出x的值为（）A．-1B．1C．3D．9【答案】C【解析】因为当x=-25时进入判断成立所以计算得到.在进入判断框，又是成立的所以.再一次进入判断框由于不成立，所以进到的运算，即可得.故选C.解题关键是要逐一代入判断计算，易出错.【考点】1.框图语言.2.循环语句.3.判断语句.26.执行如图所示的程序框图，输出的S值为（）A．B．C．D．【答案】B【解析】程序在执行过程中，的值分别为；；；；，故输出的值为.【考点】程序框图.27.执行如图所示的程序框图，输出的值为（）A．6B．24C．D．【答案】C【解析】根据框图的循环结构，依次，跳出循环，输出结果。

(完整版)高考算法程序框图真题练习及答案详解1. 该算法程序框图的功能是什么？A. 求a，b，c三数的最大数B. 求a，b，c三数的最小数C. 将a，b，c按从小到大排列2. 该算法程序框图的功能是什么？A. 求输出a，b，c三数的最大数B. 求输出a，b，c三数的最小数C. 将a，b，c按从小到大排列3. 该算法程序框图的功能是什么？A. 找出a、b、c三个数中最大的数B. 找出a、b、c三个数中最小的数C. 找出a、b、c三个数中第二大的数4. 程序框图表示的算法的运行结果是什么？A. 5B. 6C. 75. 程序框图中所表示的算法是什么？A. 求x的绝对值B. 求x的相反数C. 求x的平方根6. 运行图中所示程序框图所表达的算法，输出的结果是什么？A. 3B. 7C. 157. 程序框图（算法流程图）的输出结果是什么？A. 6B. 5C. 48. 运行相应的程序，输出的结果为什么？A. 676B. 26C. 59. 运行相应的程序，输出的结果是什么？A. 1B. 2C. 310. 运行相应的程序，输出的S的值等于什么？A. 18B. 2C. 2111. 当m=7，n=3时，执行如图所示的程序框图，输出的S的值为什么？A. 7B. 42C. 21012. 执行如图所示的程序框图，若输入n=10，则输出的S=什么？A.B.C.13. 运行相应的程序，当输入x的值为-25时，输出x的值为什么？A. -1B. 1C. 314. 运行相应的程序，输出s值等于什么？A. -3B. -10C.15. 执行如图所示的程序框图，若输入n的值为6，则输出s的值为什么？A. 105B.C. 1516. 执行如图所示的程序框图，则输出的S的值是什么？A.B. 16C.D. 1A．9B．10C．11D．12考点：循环结构．专题：程序框图．分析：根据程序框图，计算每次循环后变量a的值，直到不满足循环条件，输出结果．解答：解：根据程序框图，计算每次循环后变量a的值，直到不满足循环条件，输出结果．第一次循环：a=3+2=5第二次循环：a=5+3=8第三次循环：a=8+4=12第四次循环：a=12+5=17第五次循环：a=17+6=23第六次循环：a=23+7=30第七次循环：a=30+8=38第八次循环：a=38+9=47第九次循环：a=47+10=57此时不满足循环条件，输出a的值，为57-9=48，故选A．点评：本题考查了应用程序框图进行简单的计算问题，是基础题．并在满足条件时跳出循环，输出S的值．当k=3时，不满足条件k≥n，跳出循环，输出S=7×6×5×4=840．故选D．点评：本题考查了直到型循环结构的程序框图，根据框图的流程判断算法的功能是解题的关键．同时，需要注意条件的判断和循环变量的变化过程．解：$k=1$，满足判断框，第1次循环，$s=1$，$k=2$；第2次判断后循环，$s=0$，$k=3$；第3次判断并循环$s=-3$，$k=4$，第3次判断退出循环，输出$s=-3$。

高中算法程序框图一．选择题（共18小题）1．如图给出了一个算法程序框图，该算法程序框图的功能是（）A．求a，b，c三数的最大数B．求a，b，c三数的最小数C．将a，b，c按从小到大排列D．将a，b，c按从大到小排列2．如图给出一个算法的程序框图，该程序框图的功能是（）A．求输出a，b，c三数的最大数B．求输出a，b，c三数的最小数C．将a，b，c按从小到大排列D．将a，b，c按从大到小排列3．（2012•三明模拟）如图给出一个算法的程序框图，该程序框图的功能是（）A．找出a、b、c三个数中最大的数B．找出a、b、c三个数中最小的数C．找出a、b、c三个数中第二大的数D．把c的值赋给a4．程序框图表示的算法的运行结果是（）A．5B．6C．7D．85．程序框图中所表示的算法是（）A．求x的绝对值B．求x的相反数C．求x的平方根D．求x的算术平方根6．（2014•泉州一模）运行图中所示程序框图所表达的算法，输出的结果是（）A．3B．7C．15 D．317．（2013•合肥二模）如图所示，程序框图（算法流程图）的输出结果是（）A．6B．5C．4D．3 8．阅读如图所示的程序框图，运行相应的程序，输出的结果为（）A．676 B．26 C．5D．2 9．阅读如图所示的程序框图，运行相应的程序，输出的结果是（）A．1B．2C．3D．4 10．（2014•福建）阅读如图所示的程序框图，运行相应的程序，输出的S的值等于（）A．18 B．20 C．21 D．40 11．（2014•北京）当m=7，n=3时，执行如图所示的程序框图，输出的S的值为（）A．7B．42 C．210 D．840 12．（2013•辽宁）执行如图所示的程序框图，若输入n=10，则输出的S=（）A．B．C．D．13．（2012•天津）阅读程序框图，运行相应的程序，当输入x的值为﹣25时，输出x的值为（）A．﹣1 B．1C．3D．9 14．（2012•福建）阅读如图所示的程序框图，运行相应的程序，输出s值等于（）A．﹣3 B．﹣10 C．0D．﹣2 15．（2012•广东）执行如图所示的程序框图，若输入n的值为6，则输出s的值为（）A．105 B．16 C．15 D．1 16．（2012•辽宁）执行如图所示的程序框图，则输出的S的值是（）A．4B．C．D．﹣1 17．（2011•北京）执行如图所示的程序框图，若输入A的值为2，则输入的P值为（）A．2B．3C．4D．5 18．（2011•北京）执行如图所示的程序框图，输出的s值为（）C．D．2 A．﹣3 B．﹣二．填空题（共9小题）19．程序框图（如图所示），则该程序框图表示的算法的功能是：_________．20．有如图程序框图，则该程序框图表示的算法功能是_________．21．如图所示的程序框图，其算法功能是_________．22．（2014•许昌三模）如图所示，程序框图（算法流程图）的输出结果是_________．23．如图所示的程序框图表示的算法的结果是_________．24．某算法的程序框图如图所示，则程序输出y的值是_________．25．（2011•江西）下图是某算法的程序框图，则程序运行后所输出的结果是_________．26．（2014•惠州模拟）如图所示，程序框图（算法流程图）的输出结果为_________．27．阅读如图所示的程序框图，运行相应的程序，则输出的s值等于_________．三．解答题（共1小题）28．如图所示，程序框图（算法流程图）的输出结果是_________．参考答案与试题解析一．选择题（共18小题）1．如图给出了一个算法程序框图，该算法程序框图的功能是（）A．求a，b，c三数的最大数B．求a，b，c三数的最小数C．将a，b，c按从小到大排列D．将a，b，c按从大到小排列考点：设计程序框图解决实际问题．专题：操作型．分析：逐步分析框图中的各框语句的功能，第一个条件结构是比较a，b的大小，并将a，b中的较小值保存在变量a中，第二个条件结构是比较a，c的大小，并将a，c中的较小值保存在变量a中，故变量a的值最终为a，b，c中的最小值．由此不难推断程序的功能．解答：解：逐步分析框图中的各框语句的功能，第一个条件结构是比较a，b的大小，并将a，b中的较小值保存在变量a中，第二个条件结构是比较a，c的大小，并将a，c中的较小值保存在变量a中，故变量a的值最终为a，b，c中的最小值．由此程序的功能为求a，b，c三个数的最小数．故答案选B点评：算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．要判断程序的功能就要对程序的流程图（伪代码）逐步进行分析，分析出各变量值的变化情况，特别是输出变量值的变化情况，就不难得到正确的答案．2．如图给出一个算法的程序框图，该程序框图的功能是（）A．求输出a，b，c三数的最大数B．求输出a，b，c三数的最小数C．将a，b，c按从小到大排列D．将a，b，c按从大到小排列考点：程序框图．专题：算法和程序框图．分析：根据框图的流程判断，第一个环节的功能是输出的a是a，b之间的最大数，第二个环节功能是输出a，c 之间的最大数，由此可得答案．解答：解：由程序框图知：第一个环节是比较a，b，输出的a是a，b之间的最大数；第二个环节是比较a，c，输出的a是a，c之间的最大数．∴算法的功能是输出a，b，c三数的最大数．故选：A．点评：本题考查了排序程序框图，根据框图的流程判断算法的功能是关键．3．（2012•三明模拟）如图给出一个算法的程序框图，该程序框图的功能是（）A．找出a、b、c三个数中最大的数B．找出a、b、c三个数中最小的数C．找出a、b、c三个数中第二大的数D．把c的值赋给a考点：程序框图．专题：阅读型．分析：再输入了三个实数a、b、c后，首先对其中的两个数a、b的大小加以判断，二者取小的数，然后再比较取得的数与c的大小，再取小的数输出．解答：解：输入框中输入了三个实数a、b、c，然后首先判断a与b的大小，若a＞b成立，则用b替换a，若a≤b，不进行替换，这样再用两者之间的小的数和c比较，若a＞c，用c替换a，输出a，否则，直接输出小的数a所以程序框图的功能是找出a、b、c三个数中最小的数．故选B．点评：本题考查了程序框图中的条件结构，条件结构有两个路径，满足条件执行一个路径，不满足条件，执行另一个路径，解答本题时，一定要注意“=”的意义，是用后者替换前者．4．程序框图表示的算法的运行结果是（）A．5B．6C．7D．8考点：程序框图．专题：计算题．分析：由判断框可知：只要s≤20，则程序就执行“是”，否则就跳出循环程序，执行“否”，并输出i．据此可得出答案．解答：解：由判断框可知：只要s≤20，则程序就执行“是”，否则就跳出循环程序，执行“否”，并输出i．当s=1+2+3+4+5=15＜20，应继续执行“是”，则s=15+6=21＞20，此时i=6+1=7，要跳出循环，输出7．故选C．点评：理解循环结构的工作原理并会计算s与i是解决问题的关键．5．程序框图中所表示的算法是（）A．求x的绝对值B．求x的相反数C．求x的平方根D．求x的算术平方根考点：选择结构．专题：图表型．分析：写出经过选择结构得到的结果，得到求的y的值的形式，即可判断出框图的功能．解答：解：逐步分析框图中的各框语句的功能，该程序框图表示算法的功能是求函数y=的值，即y=|x|，故选A．点评：本题考查解决程序框图中的选择结构时，常采用写出前几次选择的结果，找规律．6．（2014•泉州一模）运行图中所示程序框图所表达的算法，输出的结果是（）A．3B．7C．15 D．31考点：程序框图．专题：算法和程序框图．分析：由算法的程序框图，计算各次循环的结果，满足条件，结束程序．解答：解：根据算法的程序框图知，第一次循环得a=2×1+1=3，第二次循环得a=2×3+1=7，第三次循环得a=2×7+1=15，结束循环，故选C，点评：本题考查了应用程序框图进行简单的计算问题，是基础题．7．（2013•合肥二模）如图所示，程序框图（算法流程图）的输出结果是（）A．6B．5C．4D．3考点：循环结构．专题：图表型．分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算i值，并输出满足条件S＞20的第一个i值，模拟程序的运行过程，用表格将程序运行过程中变量k的值的变化情况进行分析，不难给出答案．解答：解：程序在运行过程中各变量的值如下表示：s i 是否继续循环循环前 1 1/第一圈 1 2 是第二圈 2 3 是第三圈 6 4 是第四圈24 5 否故最后输出的i值为：5，故选B．点评：根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：：①分析流程图（或伪代码），从流程图（或伪代码）中即要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．8．阅读如图所示的程序框图，运行相应的程序，输出的结果为（）A．676 B．26 C．5D．2考点：循环结构．专题：图表型．分析：根据已知中的流程图，我们模拟程序的运行结果，看变量a的值是否满足判断框的条件，当判断框的条件不满足时执行循环，满足时退出循环，即可得到输出结果．解答：解：a=1，满足条件a＜15，执行循环，a=2，满足条件a＜15，执行循环，a=5，满足条件a＜15，执行循环，a=26，不满足条件a＜15，退出循环，执行输出语句，输出a=26．故选B．点评：本题主要考查的知识点是程序框图，模拟循环的执行过程是解答此类问题常用的办法，属于基础题．9．阅读如图所示的程序框图，运行相应的程序，输出的结果是（）A．1B．2C．3D．4考点：程序框图．专题：图表型．分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算S值重新为2时变量n的值，并输出，模拟程序的运行过程，即可得到答案．解答：解：程序在运行过程中各变量的值如下表示：S n 是否继续循环循环前 2 1/第一圈﹣1 2 是第二圈 3 是第三圈 2 4 否则输出的结果为4故选D点评：本题考查的知识点是程序框图，在写程序的运行结果时，模拟程序的运行过程是解答此类问题最常用的办法．10．（2014•福建）阅读如图所示的程序框图，运行相应的程序，输出的S的值等于（）A．18 B．20 C．21 D．40考点：循环结构．专题：计算题；算法和程序框图．分析：算法的功能是求S=21+22+…+2n+1+2+…+n的值，计算满足条件的S值，可得答案．解答：解：由程序框图知：算法的功能是求S=21+22+…+2n+1+2+…+n的值，∵S=21+22+1+2=2+4+1+2=9＜15，S=21+22+23+1+2+3=2+4+8+1+2+3=20≥15．∴输出S=20．故选：B．点评：本题考查了直到型循环结构的程序框图，根据框图的流程判断算法的功能是解题的关键．11．（2014•北京）当m=7，n=3时，执行如图所示的程序框图，输出的S的值为（）A．7B．42 C．210 D．840考点：循环结构．专题：计算题；算法和程序框图．分析：算法的功能是求S=7×6×…×k的值，根据条件确定跳出循环的k值，计算输出S的值．解答：解：由程序框图知：算法的功能是求S=7×6×…×k的值，当m=7，n=3时，m﹣n+1=7﹣3+1=5，∴跳出循环的k值为4，∴输出S=7×6×5=210．故选：C．点评：本题考查了循环结构的程序框图，根据框图的流程判断算法的功能是解答本题的关键．12．（2013•辽宁）执行如图所示的程序框图，若输入n=10，则输出的S=（）A．B．C．D．考点：循环结构．专题：计算题；图表型．分析：框图首先给累加变量S和循环变量i分别赋值0和2，在输入n的值为10后，对i的值域n的值大小加以判断，满足i≤n，执行，i=i+2，不满足则跳出循环，输出S．解答：解：输入n的值为10，框图首先给累加变量S和循环变量i分别赋值0和2，判断2≤10成立，执行，i=2+2=4；判断4≤10成立，执行=，i=4+2=6；判断6≤10成立，执行，i=6+2=8；判断8≤10成立，执行，i=8+2=10；判断10≤10成立，执行，i=10+2=12；判断12≤10不成立，跳出循环，算法结束，输出S的值为．故选A．点评：本题考查了循环结构中的当型循环，即先判断后执行，满足条件，执行循环，不满足条件跳出循环，算法结束，是基础题．13．（2012•天津）阅读程序框图，运行相应的程序，当输入x的值为﹣25时，输出x的值为（）A．﹣1 B．1C．3D．9考点：循环结构．专题：计算题．分析：根据题意，按照程序框图的顺序进行执行，当|x|≤1时跳出循环，输出结果．解答：解：当输入x=﹣25时，|x|＞1，执行循环，x=﹣1=4；|x|=4＞1，执行循环，x=﹣1=1，|x|=1，退出循环，输出的结果为x=2×1+1=3．故选：C．点评：本题考查循环结构的程序框图，搞清程序框图的算法功能是解决本题的关键，按照程序框图的顺序进行执行求解，属于基础题．14．（2012•福建）阅读如图所示的程序框图，运行相应的程序，输出s值等于（）A．﹣3 B．﹣10 C．0D．﹣2考点：循环结构．专题：计算题．分析：通过循环，计算s，k的值，当k=4时退出循环，输出结果即可．解答：解：k=1，满足判断框，第1次循环，s=1，k=2，第2次判断后循环，s=0，k=3，第3次判断并循环s=﹣3，k=4，第3次判断退出循环，输出S=﹣3．故选A．点评：本题考查循环结构，注意循环条件的判断，循环计算的结果，考查计算能力．15．（2012•广东）执行如图所示的程序框图，若输入n的值为6，则输出s的值为（）A．105 B．16 C．15 D．1考点：循环结构．专题：计算题；压轴题．分析：本循环结构是当型循环结构，它所表示的算式为s=1×3×5×…×（2i﹣1），由此能够求出结果．解答：解：如图所示的循环结构是当型循环结构，它所表示的算式为s=1×3×5×…×（2i﹣1）∴输入n的值为6时，输出s的值s=1×3×5=15．故选C．点评：本题考查当型循环结构的性质和应用，是基础题．解题时要认真审题，仔细解答．16．（2012•辽宁）执行如图所示的程序框图，则输出的S的值是（）A．4B．C．D．﹣1考点：循环结构．专题：阅读型．分析：根据流程图，先进行判定条件，满足条件则运行循环体，一直执行到不满足条件即跳出循环体，求出此时的S即可．解答：解：第一次运行得：S=﹣1，i=2，满足i＜6，则继续运行第二次运行得：S=，i=3，满足i＜6，则继续运行第三次运行得：S=，i=4，满足i＜6，则继续运行第四次运行得：S=4，i=5，满足i＜6，则继续运行第五次运行得：S=﹣1，i=6，不满足i＜6，则停止运行输出S=﹣1，故选D．点评：本题主要考查了当型循环结构，循环结构有两种形式：当型循环结构和直到型循环结构，当型循环是先判断后循环，直到型循环是先循环后判断，属于基础题．17．（2011•北京）执行如图所示的程序框图，若输入A的值为2，则输入的P值为（）A．2B．3C．4D．5考点：循环结构．专题：图表型．分析：根据输入A的值，然后根据S进行判定是否满足条件S≤2，若满足条件执行循环体，依此类推，一旦不满足条件S≤2，退出循环体，求出此时的P值即可．解答：解：S=1，满足条件S≤2，则P=2，S=1+=满足条件S≤2，则P=3，S=1++=满足条件S≤2，则P=4，S=1+++=不满足条件S≤2，退出循环体，此时P=4故选：C点评：本题主要考查了当型循环结构，循环结构有两种形式：当型循环结构和直到型循环结构，当型循环是先判断后循环，直到型循环是先循环后判断．18．（2011•北京）执行如图所示的程序框图，输出的s值为（）A．﹣3 B．C．D．2﹣考点：循环结构．专题：图表型．分析：i=0，满足条件i＜4，执行循环体，依此类推，当i=4，s=2，此时不满足条件i＜4，退出循环体，从而得到所求．解答：解：i=0，满足条件i＜4，执行循环体，i=1，s=满足条件i＜4，执行循环体，i=2，s=﹣满足条件i＜4，执行循环体，i=3，s=﹣3满足条件i＜4，执行循环体，i=4，s=2不满足条件i＜4，退出循环体，此时s=2故选：D点评：根据流程图计算运行结果是算法这一模块的重要题型，处理的步骤一般为：分析流程图，从流程图中即要分析出计算的类型，又要分析出参与计算的数据建立数学模型，根据第一步分析的结果，选择恰当的数学模型解模．算法和程序框图是新课标新增的内容，在近两年的新课标地区高考都考查到了，这启示我们要给予高度重视，属于基础题．二．填空题（共9小题）19．程序框图（如图所示），则该程序框图表示的算法的功能是：计算并输出使1×3×5×7×…＞10000成立的最小整数．考点：循环结构．专题：图表型．分析：写出经过几次循环得到的结果，得到求的s的形式，判断出框图的功能．解答：解：经过第一次循环得到s=1×3，i=5经过第二次循环得到s=1×3×5，i=7经过第三次循环得到s=1×3×5×7，i=8…s=1×3×5×7×…＞10000该程序框图表示算法的功能是求计算并输出使1×3×5×7×…＞10000成立的最小整数故答案为计算并输出使1×3×5×7×…＞10000成立的最小整数点评：本题考查程序框图，考查了循环体以及循环次数两个具体问题，常采用写出前几次循环的结果，找规律．属于基础题．20．有如图程序框图，则该程序框图表示的算法功能是求使不等式1×3×5×…×i≥10000成立的最小i值．考点：程序框图．专题：算法和程序框图．分析：根据框图的流程可得i的值与S的值的变化规律，再根据跳出循环的条件与输出的值，可得算法的功能．解答：解：由框图的流程知：i的值依次为3、5、7、…，∴S的值依次为1，1×3，1×3×5，…，1×3×5×…，根据退出循环的条件是S≥10000得：条件是满足不等式1×3×5×…×i≥10000，∵输出i﹣2，∴算法的功能是求使不等式1×3×5×…×i≥10000成立的最小i值．故答案为：求使不等式1×3×5×…×i≥10000成立的最小i值．点评：本题考查了循环价格的垂线框图，根据框图的流程判断i值与S值的变化规律是关键．21．如图所示的程序框图，其算法功能是计算并输出使1×3×5×7×…＞1000成立的最小整数．考点：循环结构．专题：阅读型．分析：写出经过几次循环得到的结果，得到求的s的形式，判断出框图的功能．解答：解：经过第一次循环得到s=1×3，i=5经过第二次循环得到s=1×3×5，i=7经过第三次循环得到s=1×3×5×7，i=9…s=1×3×5×7×…＞1000该程序框图表示算法的功能是求计算并输出使1×3×5×7×…＞1000成立的最小整数故答案为：计算并输出使1×3×5×7×…＞1000成立的最小整数点评：本题考查程序框图，考查了循环体以及循环次数两个具体问题，常采用写出前几次循环的结果，找规律．属于基础题．22．（2014•许昌三模）如图所示，程序框图（算法流程图）的输出结果是﹣2．考点：程序框图．专题：操作型．分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算并输出y值，模拟程序的运行过程，可得答案．解答：解：当x=1时，满足循环条件，此时x=2，y=0当x=2时，满足循环条件，此时x=4，y=﹣1当x=4时，满足循环条件，此时x=8，y=﹣2当x=8时，不满足循环条件，退出循环故输出结果为﹣2故答案为：﹣2点评：根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：：①分析流程图（或伪代码），从流程图（或伪代码）中即要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．23．如图所示的程序框图表示的算法的结果是127．考点：程序框图．专题：算法和程序框图．分析：根据框图的流程依次计算程序运行的结果，直到满足条件a＞100，跳出循环，确定输出a的值．解答：解：由程序框图知：第一次循环a=2×1+1=3；第二次循环a=2×3+1=7；第三次循环a=2×7+1=15；第四次循环a=2×15+1=31；第五次循环a=2×31+1=63；第六次循环a=63×2+1=127．满足条件a＞100，跳出循环，输出a=127．故答案为：127．点评：本题考查了循环结构的程序框图，根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法．24．某算法的程序框图如图所示，则程序输出y的值是﹣1．考点：选择结构．专题：函数的性质及应用．分析：由题意，x=﹣1，执行函数y=3x+2，代入计算可得结论．解答：解：由题意，x=﹣1，执行函数y=3x+2，代入计算可得y=﹣1故答案为：﹣1点评：本题考查选择结构，考查学生的计算能力，属于基础题．25．（2011•江西）下图是某算法的程序框图，则程序运行后所输出的结果是27．考点：程序框图．专题：计算题；阅读型．分析：根据s=0，n=1，s=（0+1）×1=1，n=1+1=2，不满足条件n＞3，执行循环体；依此类推，当n=4，满足条件n＞3，退出循环体，得到输出结果即可．解答：解：s=0，n=1，s=（0+1）×1=1，n=1+1=2，不满足条件n＞3，执行循环体；s=（1+2）×2=6，n=1+2=3，不满足条件n＞3，执行循环体；s=（6+3）×3=27，n=1+3=4，满足条件n＞3，退出循环体，则输出结果为：27故答案为：27点评：本题主要考查了直到型循环结构，循环结构有两种形式：当型循环结构和直到型循环结构，当型循环是先判断后循环，直到型循环是先循环后判断，属于基础题之列．26．（2014•惠州模拟）如图所示，程序框图（算法流程图）的输出结果为．考点：程序框图．专题：算法和程序框图．分析：根据框图的流程依次计算运行的结果，直到条件不满足，计算输出s的值．解答：解：由程序框图知：第一次循环：s=0+，n=2+2=4；第二次循环：s=+=，n=4+2=6；第三次循环：s=+=，n=6+2=8；不满足条件n＜8，程序运行终止，输出s=．故答案为：．点评：本题考查了循环结构的程序框图，根据框图的流程依次计算运行的结果是解答此类问题的常用方法．27．阅读如图所示的程序框图，运行相应的程序，则输出的s值等于46．考点：程序框图．专题：计算题．分析：①i←1，s←1，i←1+1，s←2×（1+1），判断“i＞4”，应执行“否”；…；直到“i＞4”成立即可跳出循环结构，输出s的值．解答：解：①i←1，s←1，i←1+1，s←2×（1+1），判断“i＞4”，应执行“否”；②i←2+1，s←2×（4+1），判断“i＞4”，应执行“否”；③i←3+1，s←2×（10+1），判断“i＞4”，应执行“否”；④i←4+1，s←2×（22+1），判断“i＞4”，应执行“是”．输出s←46．故答案为46．点评：本题考查了循环结构的功能，属于基础题．三．解答题（共1小题）28．如图所示，程序框图（算法流程图）的输出结果是．考点：程序框图．专题：算法和程序框图．分析：根据程序框图，程序的功能是求和由此可得结论．解答：解：根据程序框图，程序的功能是求和故答案为：．点评：本题考查循环结构，考查数列的求和，考查学生的计算能力，属于基础题．。