灵川县潭下中学2012春季学期期中考试题题目

2012—2013学年度下学期七年级数学期中试题一、选择题（共10小题，每小题3分，共30分）1、下面四个图形中，∠1与∠2是对顶角的图形是 （ ）A B C D2、如图，能判断直线AB ∥CD 的条件是 （ ）A ．∠1=∠2B ．∠3=∠4C ．∠1+∠3=180 oD ．∠3+∠4=180 o3、若a 、b 、c 为平面内三条线段，下列说法错误的是 （ ）A ．∵,,a b b c ⊥⊥∴a c ⊥B ．//,//,a b b c ∴//a cC ．∵,a b b c ==∴a c =D ．∵,a b b c ⊥⊥，∴//a c4、()20.7-的平方根是 （ ）A ．0.7-B ．0.7±C ．0.7D ．0.495、下列说法正确的是 （ ）A.064.0-的立方根是0.4B.27-立方根是3±C.16的立方根是316 D.0.01的立方根是0.0000016、有下列说法：（1）无理数就是开方开不尽的数； （2）无理数是无限不循环小数；（3）无理数包括正无理数、零、负无理数；（4）无理数都可以用数轴上的点来表示.其中正确的说法的个数是 （ ）A ．1B ．2C ．3D ．47、把点P 1（2，一3）向右平移3个单位长度再向下平移2个单位长度到达点P 2处，则P 2的坐标是（ ）A.（5，－1）B.（－1，－5）C.（5，－5）D.（－1，－1）8、已知点A （2，－3），线段AB 与坐标轴没有交点，则点B 的坐标可能是 （ ）A ．（－1，－2）B ．（ 3，－2）C ．（1，2）D ．（－2，3）9、点P （m +3，m +1）在直角坐标系的x 轴上，则P 点坐标为 （ ）A.（0，－2）B.（2，0）C.（0，2）D.（0，－4） 10、如图, 已知: AD 平分∠EAC , ∠1＋∠2＝90°, CB ⊥AB , ∠3＝∠4, 则下列结论：①AE ∥BC ; ②∠8＝12∠7; ③∠1＋∠7＝∠9; ④∠3＋∠6＝∠5. 其中正确的有（ ）A. 1个B. 2个C. 3个D. 4个二、填空题（共6小题，每小题3分，共18分）11、把“等角的补角相等”写成“如果……，那么……”形式 ． 12、如图，已知AB ∥CD ，BE 平分∠ABC ，∠CDE ＝150°，则∠C ＝______. 13、化简： .14、将下列实数“π， 3”用“＜”连接 .15、若点M 在第一、三象限的角平分线上，且点M 到x 轴的距离为2，则M 的坐标是 . 16、观察下列等式①222345+=；②22251213+=；③22272425+=；④22294041+=，…则第⑤个式子为.ABCDEN MPO BA学校 班级 姓名 考号密 封 线GF ED CBA321BA 2012—2013学年度下学期七年级数学期中答卷11.12.13. 14. 15. 16.三、解答题（共72分）17、（本题6分）计算: (1) （2）)118、（本题6分）解方程：（1）2449x - = 0 （2）()3111358x ++=-19、（本题8分，每空1分）如图EF ∥AD ，∠1=∠2，∠BAC =70°，求∠AGD . 解：∵EF ∥AD ，（已知）∴∠2= （）又∵∠1=∠2，(已知)∴∠1=∠3，( ) ∴AB ∥ （） ∴∠BAC + =180 o （）∵∠BAC =70 o ， ∴∠AGD = .20、（本题6分）如图，已知线段AB 和AB 外一点P . 根据文字描述画出图形.（1）过P 作l ∥AB ；（2）连接PB ，并反向延长PB ； （3）过A 作BP 的垂线段AC .21.（本题8分）如图，△ABC 中任意一点P （0x ，0y ）经平移后对应点为1P （0x +5，0y +3），将△ABC 作同样的平移得到△111ABC . （1）画出△111ABC ； （2）1A ，1B ，1C 的坐标分别为： 1A 1B 1C（3）求△ABC 的面积.22.（本题8分）如图，∠AOB 内有一点P ，且PM ∥AO ，PN ∥BO . 求证：∠O =∠P .xy B A–41234–1–2–31234–1–2–3–4βαOEDCBAxy4321N′M′NMDCBAyxACEO23.（本题8分）据说，我国著名数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：一个数是59319，希望求它的立方根. 华罗庚脱口而出，说出了答案. 邻座的乘客十分惊奇，忙问计算的奥秒. 你知道华罗庚是怎样迅速准确地计算出来的吗？请按照下面的问题试一试：（1）由103=1000，1003=1000000是几位数吗？答： （2）由59319的个位上的数是9的个位上的数是几吗？答： （3）如果划去59319后面的三位319得到数59，而33=27，43=64的十位上的数是几吗？答：解决问题：已知19683，110592都是整数的立方，按照上述方法，你能确定它们的立方根吗？24、（本题10分）如图：线段AB 位于平面直角坐标系中，且A （1-，3），B （2，1）. 若线段AB 经平移后得到线段AB ''（A '与A 对应，B '与B 对应）的两端点A '和B '刚好分别在x 轴、y 轴上.（1）A '的坐标 ，B '的坐标 ； （2）四边形A A 'B 'B 的面积为 ； （3）求线段AB 与y 轴的交点C 的坐标.25、（本题12分）（1）潜望镜中的两面镜子是相互平行放置的光线经过镜子反射时，∠1=∠2，∠3=∠4，进入光线AB 与离开光线CD 有什么关系？并证明.（2）两面镜子如图放置于平面直角坐标系中，进入光线AB 经BC ，到离开光线CD ，当CD ∥BE时，探索α与β的数量关系，并证明你的结论；（3）在（2）的条件下，将△ABC 沿BC 翻折，A 点落在F . 试用β表示∠EBF .密 封 线密 封 线 内 不 得 答 题C七年级数学参考答案11. 如果两个角相等，那么它们的补角也相等 12. 120° 13. 214.3＜π 15. （2，2）或（2-，2-） 16. 222116061=+三、解答题（共72分）17、 (1)32 （2）3 18、（1）27x =± （2）72x =- 19、略 20、略（每问2分） 21、（1）画图2分 （2）1(6,6)A 1(1,4)B1(4,1)C （3分） （3）Δ10.5ABCS = （3分） 22、略23、（1）两位数（1分） （2） 9（1分） （3）3 （1分） 解：∵37343=，38512=∴个位数为7，为8 又∵3328,327== 27=33464,5125== 48= （错一个扣2分）24、（1）（—3，0） （0，—2）（4分） （2）13 （3分）（3）解：连AO 、BOΔ71(12)22AOB S CO ==+∴73CO =7(0,)3C （3分）25、（1）AB ∥CD （只答平行不给分，3分） （2）3β∂= （4分）（3）①当β=30°时，F 在BE 上∠EBF=0°②当0°＜β＜30°时，F 在CD 、BE 外部∠EBF=180°-6β③当30°＜β＜45°时，F 在CD 、BE 内部 ∠EBF=6-β180°（5分） （只分两类不扣分，掉一类扣2分）。

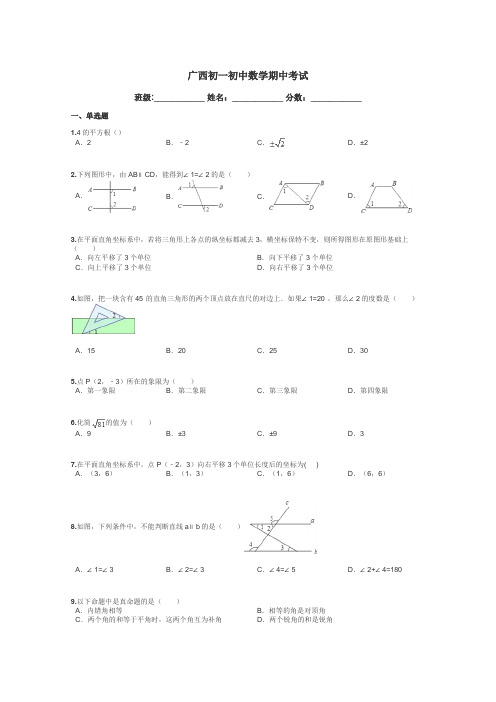
广西初一初中数学期中考试班级:___________ 姓名：___________ 分数：___________一、单选题1.4的平方根（）A．2B．﹣2C．D．±22.下列图形中，由AB∥CD，能得到∠1=∠2的是（）A．B．C．D．3.在平面直角坐标系中，若将三角形上各点的纵坐标都减去3，横坐标保特不变，则所得图形在原图形基础上（）A．向左平移了3个单位B．向下平移了3个单位C．向上平移了3个单位D．向右平移了3个单位4.如图，把一块含有45°的直角三角形的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（）A．15°B．20°C．25°D．30°5.点P（2，﹣3）所在的象限为（）A．第一象限B．第二象限C．第三象限D．第四象限6.化简的值为（）A．9B．±3C．±9D．37.在平面直角坐标系中，点P（﹣2，3）向右平移3个单位长度后的坐标为( )A．（3，6）B．（1，3）C．（1，6）D．（6，6）8.如图，下列条件中，不能判断直线a∥b的是（）A．∠1=∠3B．∠2=∠3C．∠4=∠5D．∠2+∠4=180°9.以下命题中是真命题的是（）A．内错角相等B．相等的角是对顶角C．两个角的和等于平角时，这两个角互为补角D．两个锐角的和是锐角10.下列各组数中互为相反数的是（）A．﹣2与B．﹣2与C．2与（﹣）2D．|﹣|与11.若点P（x，5）在第二象限内，则x应是（）A．正数B．负数C．非负数D．有理数12.估计的值在哪两个整数之间（）A．75和77B．6和7C．7和8D．8和9二、填空题1.﹣8的立方根是_____，36的平方根是_____．2.将点（0，1）向下平移2个单位，再向左平移4个单位后，所得点的坐标为________ .3.如图所示，想在河的两岸搭建一座桥，搭建方式最短的是_____，理由是_____．4.如图，AB∥CD，直线EF分别交AB、CD于E、F，EG平分∠BEF，若∠1＝72°，则∠2＝_________。

2024 年春部编版八年级语文下册期中试卷满分： 120 分考试时间：120 分钟一、语言的积累与运用。

（35 分）1、下列各组词语中加粗字的书写或注音无误的一组是( )A．溃退（kuì) 屏息敛声督战（dū) 残绝人寰B．颁发（bān）眼花瞭乱遗嘱（zhǔ) 殚精竭虑C．仲裁（zhōng）摧枯拉朽辱没（mò) 锐不可当D．娴熟（xián）震聋发聩悄然（qiāo）一丝不苟2、下列句子中加粗的成语使用正确的一项是( )A．虽然敌人来势凶猛，简直锐不可当，但我军顽强战斗，终于击溃了敌人的疯狂进攻。

B．近期，我县招聘了许多交通协管员，在他们的协助下，交通拥堵的现象戛然而止。

C．一些成了惊弓之鸟的部员们算也诚惶诚恐地先后把那段危险的地面通过了。

D．新版《鹿鼎记》将于2018 年6 月开拍，制作方所选的演员都是近年来炙手可热的明星。

3、下列语句没有语病的一句是( )A．当我走到路口时，看到一片热闹的景象。

B．一进屋子，我看到的第一眼是一幅油画。

C．这次比赛的胜利，将决定我们能否进入决赛阶段。

D．从咿呀学语，到走入学校，再到进入社会，学习伴随每个人的一生。

4、下列对各句所用修辞手法判断完全正确的一项是( )（1）上野的樱花烂熳的时节，望去确也像绯红的轻云。

（2）于是点上一枝烟，再继续写些为“正人君子”之流所深恶痛疾的文字。

（3）皮肤藏污纳垢，缺少光泽，就像用枝条扎成的村舍外墙那样粗糙。

（4）我一直到今天对日常生活要求不高，对吃喝从不计较，难道同我小时候的这一些经历没有关系吗？A．比喻B．拟人C．拟人D．比喻引用描写比喻反语描写比喻描写比喻比较反语反问反问5、给下列句子排序，最恰当的一项是( )①到了秋天，果实成熟，植物的叶子渐渐变黄，在秋风中簌簌地落下来。

②不久，布谷鸟也来了。

③冰雪融化，草木萌发，各种花次第开放。

再过两个月，燕子翩然归来。

④于是转入炎热的夏季，这是植物孕育果实的时期。

灵川县二年级（下册）语文期中测试试卷B卷一、倾听书写 (共1题；共5分)1. （5分）我能把字写漂亮。

辩日东游日中二、积累运用 (共6题；共64分)2. （20分）填空《赠汪伦》是________（朝代）诗人________送给他的友人________的诗歌，________,字太白，号________,世称________；3. （8分）选词填空。

温暖温和①她对人的态度总是很________，我很喜欢她。

②________的阳光照耀在大地上，到处充满了光明。

连续继续③大雨________下了三天，河水涨起来了。

④这学期王明的进步很大，他决心________努力。

4. （12分）多音字组词拧nǐng________nìng________喷pēn________pèn________薄bò________bó________báo________5. （12分）查字典“渗”按部首查字法应查________部，再查________画，组词________6. （8分） (2019二下·龙岗期中) 我会按要求做一做。

（1）我知道传统的节日。

①中秋节②重阳节③春节④元宵节⑤端午节⑥清明节A我会按时间的先后顺序排序（填序号）：________B我还知道________节时，人们会________。

（2）按要求写句子。

A例：门前开着一大片五颜六色的鲜花。

小河边________B“鼹鼠先生经过狐狸太太家，正巧，狐狸太太走出门。

”句中加点词“经过”的意思是________，用这个意思的“经过”写一个句子。

造句：________7. （4分） (2019二下·龙岗期中) 我会按课文内容填空。

（1） ________谁裁出，________似________。

（2） ________莺飞________，拂提杨柳醉________。

（3）野火烧不尽，________。

桂林市灵川县七年级上学期语文期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共1题；共2分)1. （2分） (2016七上·永定期末) 找出词性不相同的一组（）A . 游泳增加制造学习B . 慌张漂亮干净希望C . 你们咱们那样哪里D . 假如如果要是而且二、书写 (共1题；共4分)2. （4分）(2016·潮州模拟) 根据拼音写出相应的词语。

①它们虽然是哺乳动物，但在所有动物之中，甚至也包括昆虫在内，是繁殖能力最强的动物、也许只有细菌分裂才能和它们相pì měi________。

②伏尔泰具有女性的温情和英雄的怒火，他具有伟大的头脑和hào hàn________无际的心胸。

③音乐行弦，水上漂shuì yǎn xīnɡ sōnɡ________嘀咕。

④仰之弥高，越高，攀得越起劲；钻得弥坚，越坚，钻得越qiè ér bù shě________。

三、默写 (共1题；共6分)3. （6分）根据课文默写：①________，乌蒙磅礴走泥丸。

②感时花溅泪，________ 。

③________，夜泊秦淮近酒家。

④白头搔更短，________。

⑤龚自珍在《己亥杂诗》中运用比喻、融入议论、表明心志的句子是________ 。

⑥陆游《十一月四日风雨大作》中把现实与梦境自然地联系起来以抒发强烈爱国之情的句子是________ 。

四、名著导读 (共1题；共15分)4. （15分）名著阅读。

（1）阅读下段文字，回答文后问题。

行者笑道：“嫂嫂勿得悭吝，是必借我使使。

保得唐僧过山，就送还你。

我是个志诚有余的君子，不是那借物不还的人。

”罗刹又骂道：“泼猢狲！好没道理，没分晓！夺子之仇，尚未报得；借扇之意，岂得如心！你不要走！吃我老娘一剑。

”这段文字出自《西游记》哪一个情节？罗刹说的“夺子之仇”是指什么？情节：“夺子之仇”是指：（2）阅读下面几段《草房子》中的文字，填写人名。

桐城市练潭初中2011~2012学年第二学期期中考试试卷七 年 级 数 学（考试时间:120分钟 满分:150分）一、选择题：（本大题共10小题，每小题4分，满分40分）1、在实数1415926.3,27,2,3.0,23π∙-中，无理数有 （ ）A ．1个B ．2个C ．3个D ．4个2、－27的立方根与81的平方根之和是（ A 、0 B 、－6 C 、0或－6 D 、63、在x 1·21，212+x ，πxy 3，yx +3，a+m 1中，分式的个数有（ ）A 、2个B 、3个C 、4个D 、5个4.、生物小组要在温箱里培养A 、B 两种菌苗，A 种菌苗的生长温度)(C x ︒的范围是3835≤≤x ，B 种菌苗的生长温度)(C y ︒的范围是3436y ≤≤，那么温箱里的温度)(C T ︒应该设定的范围是 （ ）A ．3835≤≤TB ．3635≤≤TC ．3634≤≤TD ．3836≤≤T5、关于不等式a x +-2≥2的解集如图所示，则a 的值是（ ）A 、0B 、2C 、－2D 、－46.下列运算正确的是 （ ）A.3412a a a ⋅= .B.3362a a a +=C.330a a ÷=D.2353515x x x ⋅=7. 1nm(纳米)=0.000000001m,则2.5纳米用科学记数法表示为( )A.2.5×10-8mB.2.5×10-9mC.2.5×10-10mD.0.25×10-9m8．已知230.5x y z==，则32x y z x y z +--+的值是（ ）A ．17 B.7 C.1 D.139. 下列等式中正确的是（ ）A 、1-=-+-ba ba B 、0=++ba baC 、ba b a b a ba +-=+-232.03.01.0 D 、ba ba b a ba -+=-+3121 10. 如图是测量一颗玻璃球体积的过程：（1）将300ml 的水倒进一个容量为500ml 的杯子中； （2）将四颗相同的玻璃球放入水中，结果水没有满； （3）再加一颗同样的玻璃球放入水中，结果水满溢出．根据以上过程，推测这样一颗玻璃球的体积在（ ）Ａ．20cm 3以上，30cm 3以下 Ｂ．30cm 3以上，40cm 3以下Ｃ．40cm 3以上，50cm 3以下 Ｄ．50cm 3以上，60cm 3以下二、填空题（本大题共4小题，每小题5分，满分20分．）27 23x x--≤11.不等式的正整数解是。

桂林市灵川县七年级上学期语文期中质量检测试卷姓名:________ 班级:________ 成绩:________一、积累 (共4题；共16分)1. （2分）下列字形有误的一项是（）A . 装饰缴租闪烁B . 热忱俱集哀思C . 纯粹点缀蹒跚D . 贫贱狭隘拘谨2. （2分）(2014·枣庄) 下列选项中的成语，全是贬义的一项是（）A . 狼心狗肺虎头蛇尾蛇蝎心肠B . 凤毛麟角童颜鹤发一丘之貉C . 乌合之众狼狈为奸犬马之劳D . 狐朋狗友金鸡独立牛鬼蛇神3. （2分）(2016·杭州模拟) 下列各句中，没有语病的一句是（）A . 大师的这段经历非常重要，但流传的说法不一，而所有的当事人、知情人都已去世。

我们斟酌以后拟采用大师儿子所讲的为准。

B . 我们说话写文章，在把零散的的词语串成一个个可以用来传递信息、完成交际任务的句子的时候，是需要遵循一定的语法规律的。

C . 该厂狠抓生产质量，重视企业文化，十几年来凝聚了一批技术骨干，所生产的内衣产量成为全国同行业销售额率先突破十亿大关的一个著名品牌。

D . 一些边远山区的教师，在长年发不出工资的情况下仍辛勤工作在自己的岗位上，这种精神实在令人可敬。

4. （10分）(2018七下·肇源期末) 用课文原句填空。

（1）五岭逶迤腾细浪，________。

（毛泽东《七律长征》）（2） ________，坐断东南战未休。

（辛弃疾《南乡子登京口北固亭有怀》）（3）当窗理云鬓，________。

（《木兰诗》）（4） ________，浅草才能没马蹄。

（白居易《钱塘湖春行》）（5）角声满天秋色里，________。

（李贺《雁门太守行》）（6） ________，寡人反取病焉。

（《晏子使楚》）（7）王勃《送杜少府之任蜀川》中“________，________”两句，成为远隔千山万水的朋友之间表达深情厚谊的不朽名句。

（8）杜甫《望岳》中“________，________”两句，不仅写出了泰山的雄伟，也表现出了诗人的心胸气魄。

2023-2024学年广西桂林市灵川县高一下册期中考试数学试题一、单选题1．与80-︒角终边相同的角是（）A ．80︒B ．280︒C ．240︒D ．100︒【正确答案】B【分析】由终边相同角的概念即可得出答案.【详解】解：因为与80-︒角终边相同的角是80360,Z k k -︒+︒∈，所以与80-︒角终边相同的角是280︒.故选：B.2．函数4sin 3y x =+在[],ππ-上的递增区间为（）A ．,2ππ⎡⎤--⎢⎥⎣⎦B ．,22ππ⎡⎤-⎢⎥⎣⎦C ．,2ππ⎡⎤-⎢⎥⎣⎦D ．,2ππ⎡⎤⎢⎥⎣⎦【正确答案】B【分析】根据正弦函数图象求单调区间即可【详解】sin y x =的递增区间就是4sin 3y x =+的递增区间，由三角函数图象可得sin y x =在,2ππ⎡⎤--⎢⎥⎣⎦上递减，在,22ππ⎡⎤-⎢⎥⎣⎦上递增，在,2ππ⎡⎤⎢⎥⎣⎦上递减，故选：B ．3．下列关于向量a ，b的命题中，正确的是（）A ．若||||a b =，则a b=B ．若||||a b > ，则a b>C ．若a b =，则//a bD ．若//a b ，则a 与b夹角是0【正确答案】C【分析】结合平面向量中相等向量的概念，平行向量的概念以及平面向量的夹角的定义逐项分析即可求出结果.【详解】因为||||a b = ，但是a ，b 的方向不确定，故a ，b不一定相等，故A 错误；因为向量不能比较大小，故B 错误；因为a b =，即a ，b 的方向相同，所以//a b ，故C 正确；因为//a b ，则a ，b 的方向相同或相反，所以a 与b夹角是0或π，故D 错误；故选：C.4．已知角α的终边过点(4)(0)P m m ≠，，且sin 5mα=，则cos α的值为（）A ．35±B ．35-C ．45±D ．45【正确答案】D【分析】根据三角函数的定义，由sin α求得参数m ，再求cos α即可.【详解】角α的终边过点(4)(0)P m m ≠，，故可得sin 5mα==，解得29m =.故cos 5α==.故选：D.5．要得到sin(2)3y x π=-的图象,需要将函数sin 2y x =的图象（）A ．向左平移3π个单位B ．向右平移3π个单位C ．向左平移6π个单位D ．向右平移6π个单位【正确答案】D【分析】根据三角函数的图象变换的原则，准确化简，即可求解.【详解】根据三角函数的图象变换的原则，将函数sin 2y x =的图像向右平移6π个单位后，可得到sin 2sin(2)63y x x ππ⎛⎫=-=- ⎪⎝⎭.故选：D.6．设21,e e是平面内所有向量的一组基底，则下列四组向量中，不能作为基底的一组是（）A ．122e e - 和2124e e - B ．122e e - 和1e C ．12e e + 和122e e -D ．12e e + 和212e e + 【正确答案】A【分析】能作为平面的一个基底的两个向量必不共线，因此只需要判断选项中向量是否共线即可.【详解】对于A ，因为()21122422e e e e -=-- ，所以122e e - 和2124e e - 共线，则这组向量不能作为平面内的一组基底，故A 正确；对于B ，假设122e e - 和1e共线，则()1212R e e e μμ-=∈ ，故()1212e e μ-= ，所以21,e e共线，这与题设矛盾，所以假设不成立，则122e e - 和1e能作为平面内的一组基底，故B 错误；对于C ，假设12e e + 和122e e -共线，则()()12121222R e e e e e e λλλλ+=-=-∈ ，即()()21121e e λλ+=- ，由于12λ+与1λ-不能同时为0，所以21,e e共线，这与题设矛盾，所以假设不成立，则12e e + 和122e e -能作为平面内的一组基底，故C 错误；对于D ，假设12e e + 和212e e +共线，则()()222111R 2e e e k k e e ke k +==++∈ ，即()()1221k e k e -=- ，由于2k -与1k -不能同时为0，所以21,e e共线，这与题设矛盾，所以假设不成立，则12e e + 和212e e +能作为平面内的一组基底，故D 错误.故选：A.7．已知(3,2)a = ，(,1)b m =- ，若a b ⊥，则m =（）A ．32B ．32-C ．23D ．23-【正确答案】C【分析】由向量垂直的坐标表示求解【详解】由题意得320a b m ⋅=-= ，得23m =故选：C8．已知1sin ,cos ,tan 226a b c π===，则a ､b ､c 的大小关系为（）A ．a b c <<B ．a c b <<C ．c<a<bD ．c b a<<【正确答案】C【分析】根据正弦函数、正切函数的性质计算可得；【详解】解：因为126π<，sin y x =在0,2π⎛⎫⎪⎝⎭上单调递增，所以1sin 0sin sin 26π<<，即102b <<，1cos622b π==>，又22ππ<<，所以tan 20<，所以b a c >>；故选：C9．若扇形的面积是4cm 2，它的周长是10cm ，则扇形圆心角的弧度数为（）A ．12B ．8C ．12或8D ．2或18【正确答案】A设扇形的半径为r ，圆心角为α，由题意列出关于r 与α的方程组，求解即可得出答案．【详解】解：设扇形的半径为r ，圆心角为α，由题意得2142210r r r αα⎧=⎪⎨⎪+=⎩，解得124r α⎧=⎪⎨⎪=⎩或81r α=⎧⎨=⎩（舍去)，∴扇形圆心角的弧度数为12，故选：A ．本题主要考查扇形的弧长公式与面积公式，属于基础题．10．“cos α=是“6πα=”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【正确答案】B【分析】根据给定条件利用充分条件和必要条件的定义直接判断即可.【详解】若6πα=，则cos α=cos α=α可以取6π-，即6πα=不一定成立，所以“cos α=是“6πα=”的必要不充分条件.故选：B.11．已知函数f (x )＝2cos(3x －4π)，下面结论错误的是()A ．函数的最小正周期为23πB ．函数图像关于(－12π，0)中心对称C ．函数图像关于直线x ＝4π对称D ．将y ＝2cos3x 图像上的所有点向右平移34π，可得到函数y ＝f (x )的图像【正确答案】C【分析】A ：y ＝A cos(ωx ＋φ)＋B 的最小正周期为2πω；B ：f (x )的对称中心处函数值为零；C ：f (x )的对称轴过函数图像最高点或最低点；D ：根据函数图像平移对解析式的影响“左加右减”即可判断﹒【详解】A ：y ＝A cos(ωx ＋φ)＋B 的最小正周期为2πω，∴f (x )的最小正周期T ＝2π3，A 正确；B ：f (－12π)＝2cos[3×(－12π)－4π]＝0，所以(－12π，0)是f (x )的中心对称，B 正确；C ：f (4π)＝0，所以f (x )关于(4π，0)中心对称，C 错误；D ：将y ＝2cos3x 图像上的所有点向右平移34π变为y ＝2cos3(x －34π)＝2cos(3x －4π)，D 正确﹒故选：C ．12．在ABC 中，角,,A B C 的对边为,,a b c ，若1,2b a c ==，则当C 取最大值时，ABC 的面积是（）AB ．6C D 【正确答案】B【分析】由余弦定理可得：11cos (3)4C c c=+，再利用基本不等式的性质可得C 的最大值，再利用三角形面积计算公式即可得出．【详解】解：在ABC 中，由余弦定理可得：22222(2)1111cos (3)22244a b c c c C c ab c c +-+-===+⨯⨯当且仅当3c =时取等号．(0,)C π∈ ∴06Cπ<，∴当C 取最大值6π时，ABC 的面积11sin 26S π=⨯⨯=．故选：B ．二、多选题13．已知,2k x x k Z π⎧⎫≠∈⎨⎬⎩⎭，则函数|sin ||cos |2|sin cos |sin cos sin cos x x x x y x x x x =+-的值可能是（）A ．0B ．4-C ．4D ．2【正确答案】ABD【分析】对x 分四个象限讨论即可．【详解】解：因为,2k x x k Z π⎧⎫≠∈⎨⎬⎩⎭，所以sin 0x ≠且cos 0x ≠，当x 是第一象限角时：sin 0x >，cos 0x >，sin cos 0x x >|sin ||cos |2|sin cos |1120sin cos sin cos x x x x y x x x x=+-=+-=，当x 是第二象限角时：sin 0x >，cos 0x <，sin cos 0x x <|sin ||cos |2|sin cos |1122sin cos sin cos x x x x y x x x x=+-=-+=，当x 是第三象限角时：sin 0x <，cos 0x <，sin cos 0x x >|sin ||cos |2|sin cos |1124sin cos sin cos x x x x y x x x x =+-=---=-，当x 是第四象限角时：sin 0x <，cos 0x >，sin cos 0x x <|sin ||cos |2|sin cos |1122sin cos sin cos x x x x y x x x x=+-=-++=，所以函数的值域{}0,2,4y ∈-，故选：ABD14．已知向量(2,1)a =，(3,1)b =- ，则（）A ．()a b a+⊥ B ．|2|6a b +=C ．向量a 在向量b 上的投影向量是62(,)55-D．()55是向量a 的单位向量【正确答案】AD【分析】根据向量坐标的线性运算及数量积的坐标运算即可判断判断A ；根据向量坐标的线性运算及向量的模的坐标运算即可判断判断B ；根据投影向量的计算公式即可判断C ；判断向量()55是否与向量a 共线，及模是否为1，即可判断D.【详解】解：对于A ，()1,2a b +=- ，则()220a b a +⋅=-+=，所以()a b a +⊥，故A 正确；对于B ，()24,3a b +=- ，则|2|5a b +=，故B 错误；对于C ，向量a 在向量b上的投影向量为531cos ,,1022b a b b b a a b b b b ⋅-⎛⎫⋅⋅=⋅==- ⎪⎝⎭，故C 错误；对于D，因为向量的模等于1，120-=，所以向量与向量a共线，故是向量a 的单位向量，故D 正确.故选：AD.15．在ABC 中，D ，E ，F 分别是边BC ，CA ，AB 的中点，点G 为ABC 的重心，则下述结论中正确的是（）A ．AB BC CA += B ．()12AG AB AC =+C ．0AF BD CE ++= D ．0GA GB GC ++= 【正确答案】CD【分析】根据向量的加法运算、相反向量、中线的向量表示，重心的性质分别计算求解.【详解】由D ，E ，F 分别是边BC ，CA ，AB 的中点，点G 为ABC 的重心，因为AB BC AC CA →+=≠，故A 错误；由()12AB AC AD AG →→+=≠,故B 错误；因为()102AF BD CE AB BC CA ++=++=,故C 正确；因为2111+3222GA GB GC AB AC BA BC CA CB →→→→→→⎡⎤⎛⎫⎛⎫⎛⎫++=-++++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ 103AB BA BC CB AC CA →→→→→→→⎛⎫=-+++++= ⎪⎝⎭,故D 正确.故选：CD 三、填空题16．已知tan α=，且α为第四象限角，则cos α=____________【正确答案】12【分析】首先求α的值，再求cos α.【详解】tan α= α为第四象限角，2,3k k Z παπ∴=-+∈，1cos 2α∴=.故1217．在ABC 中，213,,cos 34ACBC AC C ===，则AB =__________.【分析】根据213,2,cos 34ACBC AC C ====，利用余弦定理求解.【详解】在ABC 中，因为213,2,cos 34AC BC AC C ====，由余弦定理得：2222cos AB AC BC AC BC C =+-⋅⋅，22132232104=+-⨯⨯⨯=，所以AB =，故18．已知(1,2),(1,),(3,4)A B x C -三点共线，则x =____.【正确答案】0【分析】AB t AC =列方程来求得x .【详解】依题意：(1,2),(1,),(3,4)A B x C -三点共线，所以AB t AC = ，即()()()2212,22,22,2,220t t x t t t x t x -==-⎧⎧--==⇒⎨⎨-==⎩⎩.故019．函数y _____________________．【正确答案】()52,2Z 66k k k ππππ⎡⎤++∈⎢⎥⎣⎦【分析】由2sin 10x -≥，可得1sin 2x ≥，结合正弦函数的性质，即可得到所求定义域．【详解】解：依题意可得2sin 10x -≥，可得1sin 2x ≥，解得52266k x k ππππ+≤≤+，Z k ∈，所以函数的定义域为()52,2Z 66k k k ππππ⎡⎤++∈⎢⎥⎣⎦.故()52,2Z 66k k k ππππ⎡⎤++∈⎢⎥⎣⎦．20．已知函数()()3sin 06f x x ωωπ⎛⎫=-> ⎪⎝⎭和()()3cos 2g x x ϕ=+的图象完全相同，若0,2x π⎡⎤∈⎢⎥⎣⎦，则()f x 的取值范围是______.【正确答案】3,32⎡⎤-⎢⎥⎣⎦【分析】利用诱导公式将正弦型函数化余弦型求出ω，再利用正弦函数的图象即可求出值域.【详解】解：因为()23sin 3cos 3cos 6263f x x x x ωωωπ⎡ππ⎤π⎛⎫⎛⎫⎛⎫=-=--=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，所以2ω=，则()3sin 26f x x π⎛⎫=- ⎪⎝⎭.因为0,2x π⎡⎤∈⎢⎥⎣⎦，所以52666x πππ-≤-≤，所以1sin 2126x π⎛⎫-≤-≤ ⎪⎝⎭，所以()332f x -≤≤.故答案为.3,32⎡⎤-⎢⎥⎣⎦四、解答题21．已知||4a = ，||2b =r ，且a 与b夹角为120°．求：(1)(2)()a b a b -⋅+；(2)|2|a b - 【正确答案】(1)12(2)【分析】（1）（2）利用向量的数量积的定义与运算法则，结合转化法即可得解.【详解】（1）因为||4a = ，||2b =r ，,120a b =︒ ，所以222216,4a a b b ==== ，1cos ,4242a b a b a b ⎛⎫⋅==⨯⨯-=- ⎪⎝⎭，所以()22(2)()21642412a b a b a a b b -⋅+=-⋅-=---⨯=.（2）因为()()2222224416444844a b a ba ab b -=--⋅+=⨯-⨯-+== ，所以2a b -= 22．已知α是第三象限的角，()()()()π3πsin cos tan π22tan 2πsin πf αααααα⎛⎫⎛⎫-⋅+⋅- ⎪ ⎪⎝⎭⎝⎭=-⋅--．(1)化简()f α；(2)若3π1cos 25α⎛⎫-= ⎪⎝⎭，求π2f α⎛⎫+ ⎪⎝⎭的值．【正确答案】(1)()cos f αα=-(2)15-【分析】利用三角函数的诱导公式化简求值即可；【详解】（1）依题意，得()()()()π3πsin cos tan π22tan 2πsin πf αααααα⎛⎫⎛⎫-⋅+⋅- ⎪ ⎪⎝⎭⎝⎭=-⋅--()()()πsin sin tan 2tan sin π2πααααα⎛⎫--⋅⋅- ⎪⎝⎭=-⋅--+()()cos sin tan tan sin πααααα-⋅⋅-=-⋅-cos sin tan cos tan sin αααααα==--.（2）因为3π3ππ1cos cos 2πcos sin 2225αααα⎛⎫⎛⎫⎛⎫-=-+=+=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以1sin 5α=-，所以ππ1cos sin 225f ααα⎛⎫⎛⎫+=-+==- ⎪ ⎪⎝⎭⎝⎭.23．在ABC 中，已知4BC =，3AC =，P 在线段BC 上，且13BP BC = ，23AQ AB = ，设CB a =，CA b =．(1)用向量a ，b表示AP ；(2)若60ACB ∠=︒，求AP CQ ⋅．【正确答案】(1)23AP a b=- (2)139【分析】（1）根据向量的线性运算直接计算；（2）利用基底法求向量的数量积.【详解】（1）由题得2233AP CP CA CB CA a b =-=-=- ；（2）由已知得()222121333333CQ CA AQ CA AB CA CB CA CB CA a b =+=+=+-=+=+22221441333993AP CQ a b a b a a b b⎛⎫⎛⎫∴⋅=-⋅+=-⋅- ⎪ ⎪⎝⎭⎝⎭ 2244113443cos 6039939=⨯-⨯⨯︒-⨯=.24．已知函数()2sin 24f x x π⎛⎫=- ⎪⎝⎭，求：（1）()f x 的最小正周期；（2）()f x 的单调递增区间；（3）()f x 取最大值时自变量x 的集合.【正确答案】（1）π；（2）5,()88k k k ππππ⎡⎤--∈⎢⎥⎣⎦Z ；（3）,8x x k k ππ⎧⎫=-∈⎨⎬⎩⎭Z .【分析】利用诱导公式化简得到()32sin 24f x x π⎛⎫=+⎪⎝⎭，再利用正弦函数的性质求解.【详解】由诱导公式得()f x 2sin 24x π⎛⎫=- ⎪⎝⎭32sin 22sin 244x x πππ⎡⎤⎛⎫⎛⎫=--=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.（1）由22T ππ==，得()f x 的最小正周期为π.（2）由3222()242k x k k πππππ-++∈Z ，得5()88k x k k ππππ--∈Z .因此()f x 的单调递增区间为5,()88k k k ππππ⎡⎤--∈⎢⎥⎣⎦Z .（3）由322()42x k k πππ+=+∈Z ，解得()8x k k ππ=-∈Z .故()f x 取最大值时自变量x 的集合为,8x x k k ππ⎧⎫=-∈⎨⎬⎩⎭Z .25．已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>><⎪⎝⎭的部分图象，如图所示.(1)求函数()f x 的解析式；(2)将函数()f x 的图象向右平移3π个单位长度，再将得到的图象上各点的横坐标缩短为原来的12，纵坐标不变，得到函数()g x 的图象，当0,3x π⎡⎤∈⎢⎣⎦时，求函数()g x 的值域.【正确答案】(1)()323f x x π⎛⎫=+ ⎪⎝⎭(2)332⎡-⎢⎣【分析】（1）根据正弦型函数的图像求三角函数的解析式，根据最大值求出A ，由最小正周期求出ω，并确定ϕ.（2）根据平移后得到新的正弦型函数解析式，由函数解析式求出函数值域.【详解】（1）解：根据函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>><⎪⎝⎭的部分图象可得3A 1252632ππππω=-=⋅，所以2ω=.再根据五点法作图可得23πϕπ⋅+=，所以3πϕ=，()323f x x π⎛⎫=+ ⎪⎝⎭.（2）将函数()f x 的图象向右平移3π个单位后，可得323sin 2333y x x x πππ⎡⎤⎛⎫⎛⎫=-+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图象，再将得到的图象上各点的横坐标缩短为原来的12，纵坐标不变，得到函数()343g x x π⎛⎫- ⎪⎝⎭的图象.由0,3x π⎡⎤∈⎢⎣⎦，可得4,33x πππ⎡⎤-∈-⎢⎥⎣⎦又 函数()g x 在50,24π⎡⎤⎢⎥⎣⎦上单调递增，在5,243ππ⎡⎤⎢⎥⎣⎦单调递减∴3(0)2g =-，5324g π⎛⎫= ⎪⎝⎭03g π⎛⎫= ⎪⎝⎭∴3()34,332g x x π⎛⎫⎡⎤=-∈- ⎪⎢⎥⎝⎭⎣⎦∴函数()g x 在0,3π⎡⎤⎢⎣⎦的值域32⎡-⎢⎣.26．为迎接2022年的亚运会，城市开始规划公路自行车比赛的赛道，该赛道的平面示意图为如图所示的五边形ABCDE .运动员在公路自行车比赛中如出现故障，可以在本队的器材车､公共器材车或收容车上获得帮助，也可以从固定修车点上获得帮助.另外，为满足需求，还需要运送一些补给物品，例如食物､饮料､工具和配件.所以项目设计需要预留出赛道内的两条服务通BD ，BE （不考虑宽度），已知E D C B A E -----为赛道，23BCD BAE π∠=∠=，4CBD π∠=，CD =，8km DE =.(1)若712∠=CDE π，求服务通道BE 的长度；(2)在（1）的条件下，应该如何设计，才能使折线赛道B A E --最长（即+BA AE 最大）？最长为多少？【正确答案】(1)10km ；(2)当3AB AE ==，折线赛道B A E --.【分析】（1）由正弦定理可得6BD =，结合已知可得2BDE π∠=，应用勾股定理即可求服务通道BE的长度；（2）由余弦定理可得22()BE AB AE AB AE =+-⋅，结合（1）及基本不等式可得22()()1004AB AE AB AE ++≤+，即可得B A E --最长长度，注意不等式中等号成立条件.【详解】（1）在△BCD 中，由正弦定理得.2sin 362sin sinsin344CD BD CDBD ππππ⋅=⇒==而23412BDC ππππ∠=--=，则712122BDE πππ∠=-=，在Rt BDE中，10km BE ==，故服务通道BE 的长度为10km .（2）在△ABE 中，由余弦定理得22222222cos()3BE AB AE AB AE AB AE AB AE AB AE AB AE π=+-⋅=++⋅=+-⋅，所以22()()1001004AB AE AB AE AB AE ++=+⋅≤+，则2400()3AB AE +≤，所以AB AE +≤AB AE ==.故AB AE ==，折线赛道B A E --.。

2012年桂林市初中毕业升学考试试卷语文（用时：150分钟满分：120分）注意事项:1．试卷分为试题卷和答题卡两部分，在本试题卷上作答无效．．．．．．．．．．。

2．答题前，请认真阅读答题卡．．．上的注意事项。

3．考试结束后，将本试卷和答题．．．．．．卡．一并交回。

第I卷:选择题(共30分，请用2B铅笔把答题卡上对应题目的答案标号涂黑)一、基础知识及运用（每小题2分，共12分）1．下列句子中加点字读音有误的一项是（2分）A.我们无论学习还是工作，都需要有锲．（qiè）而不舍的精神。

B.荣誉的桂冠用荆棘编织，胜利的鲜花在血汗中绽．（dìn g）放。

C.樟树、松树、桂树、丁香等树能分泌．（mì）含有挥发性植物杀菌素的物质。

D.到过桂林旅行的人，常被她山清、水秀、洞奇、石美的魅．（mèi）力所折服。

2．下列句子中加点词语运用错误的一项是（2分）A.我国幅员辽阔，物种丰富，发展特色农业要因地制宜．．．．。

B.刘教授回到阔别已久的家乡，睹物思人，禁不住潸然泪下．．．．。

C.在桂林市中学生曲艺大赛中，我校以别具匠心．．．．的构思获得一等奖。

D.在科技高速发展的时代，我们要努力攀登科学高峰，不能高山仰止．．．．。

3．下列语境中说话得体的一项是（2分）A．你对一位获奖的同学说：“祝贺你！有什么经验向我介绍介绍好吗？”B．你已经交了作业，科代表仍在追要，你说：“难道你让我交两遍不成？”C．同学邀你到他家去玩，你说：“行，届时我一定光临寒舍。

”D．你对夜深仍在大声说话、喧闹的邻居说：“不要讲话了，我们需要休息了。

”4．排序正确的一项是（2分）①清风拂过，细纱在空中荡开，又滑下来。

②这雨丝，是漓江之畔的苗女刚刚从碧水中拎起的那缕柔柔细细的纱。

③然后悄悄洒向扁舟，洒向村落，洒向群山。

④她伸展开手臂，轻轻地把细纱挂向云端。

⑤春雨如丝。

A.⑤①②④③B.⑤②④③①C.⑤②④①③D.⑤①④②③5．下列关于文学文化常识的表述有误的一项是（2分）A.《钦差大臣》《给巴特勒的信》的作者分别是英国的果戈理和法国的雨果。

姓名______ 准考证号______山西省2024—2025学年七年级第一学期阶段性质量检测地理（人教版）注意事项：1.本试卷分为第Ⅰ卷和第Ⅱ卷两部分。

全卷共6页，满分50分，考试时间60分钟。

2.答卷前，考生务必将自己的姓名、准考证号填写在本试卷相应的位置。

答案全部在答题卡上完成，答在本试卷上无效。

第Ⅰ卷选择题（共15分）一、选择题（每小题的四个选项中，只有一项符合题意，请选出并在答题卡上将该选项涂黑。

本大题包含15个小题，每小题1分，共15分。

）月球是地球的天然卫星，其重力只有地球的1/6，昼夜温差可达300℃。

2024年9月28日，中国登月服外观首次公开。

下图为太阳系示意图（图1）和中国登月服图片（图2）。

据此，完成1~3题。

图1 图21.宇航员登陆月球后将（）A.脱离地月系B.脱离银河系C.仍处于太阳系D.与地球失去联系2.月球表面自然环境复杂，登月服需应对（）A.野生动物的威胁B.其他恒星的撞击C.较大重力的影响D.剧烈的温度变化3.我国计划于2030年前实现载人登月开展科学探索，这有利于（）①推动科技进步②近期移民月球③认识宇宙环境④开发生物资源A.①②B.①③C.②④D.③④2024年9月3日9时，台风“摩羯”进入我国南海海域。

下图示意台风“摩羯”部分行进路线。

据此，完成4~6题。

4.②地的经纬度位置大致是（）A.（19°S，115°E）B.（19°S，115°W）C.（19°N，115°E）D.（19°N，115°W）5.图中台风“摩羯”行进路线经过的地区位于（）A.低纬度B.中纬度C.北温带D.南温带6.台风“摩羯”的行进方向大致是（）A.自西南向东北B.自东南向西北C.自西北向东南D.自东北向西南2024年10月15日，我国在太原卫星发射中心使用长征六号甲运载火箭，成功将千帆极轨02组18颗卫星发射升空。